山东省泰安市高新区2021-2022学年七年级下学期期末数学试题(word版含答案)
文档属性
| 名称 | 山东省泰安市高新区2021-2022学年七年级下学期期末数学试题(word版含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 1.4MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 鲁教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-07-07 15:54:38 | ||
图片预览

文档简介
2021—2022学年下学期期末质量检测
初二数学练习题
(考试时间120分钟,满分150分)
本试题分Ⅰ、Ⅱ卷,第Ⅰ卷为选择题,48分;第Ⅱ卷为非选择题,102分。全卷满分150分。
第Ⅰ卷(选择题)
一、选择题(本大题共12小题,在每小题给出的四个选项中,只有一个是正确的,请把正确的选项选出来,每小题选对得4分,错选、不选或选出的答案超过一个,均记零分)
1.下列命题中,真命题是( )
A.两条直线被第三条直线所截,同位角相等
B.等腰三角形的高线、中线、角平分线互相重合
C.在同一平面内,过一点有且只有一条直线与已知直线垂直
D.若,则且
2.已知,则下列不等式中错误的是( )
A. B. C. D.
3.如图,已知交于点O,,,,则的大小为( )
A.10° B.15° C.25° D.30°
4.下列事件中属于不可能事件的是( )
A.数学测验中,小明数学成绩100分
B.任选13个人,至少有2个人的出生月份相同
C.任取两个正整数,其和小于1
D.乘公交车到十字路口,遇到红灯
5.一只苍蝇飞到如图所示的一面墙上,最终停在白色区域上的概率是( )
A. B. C. D.
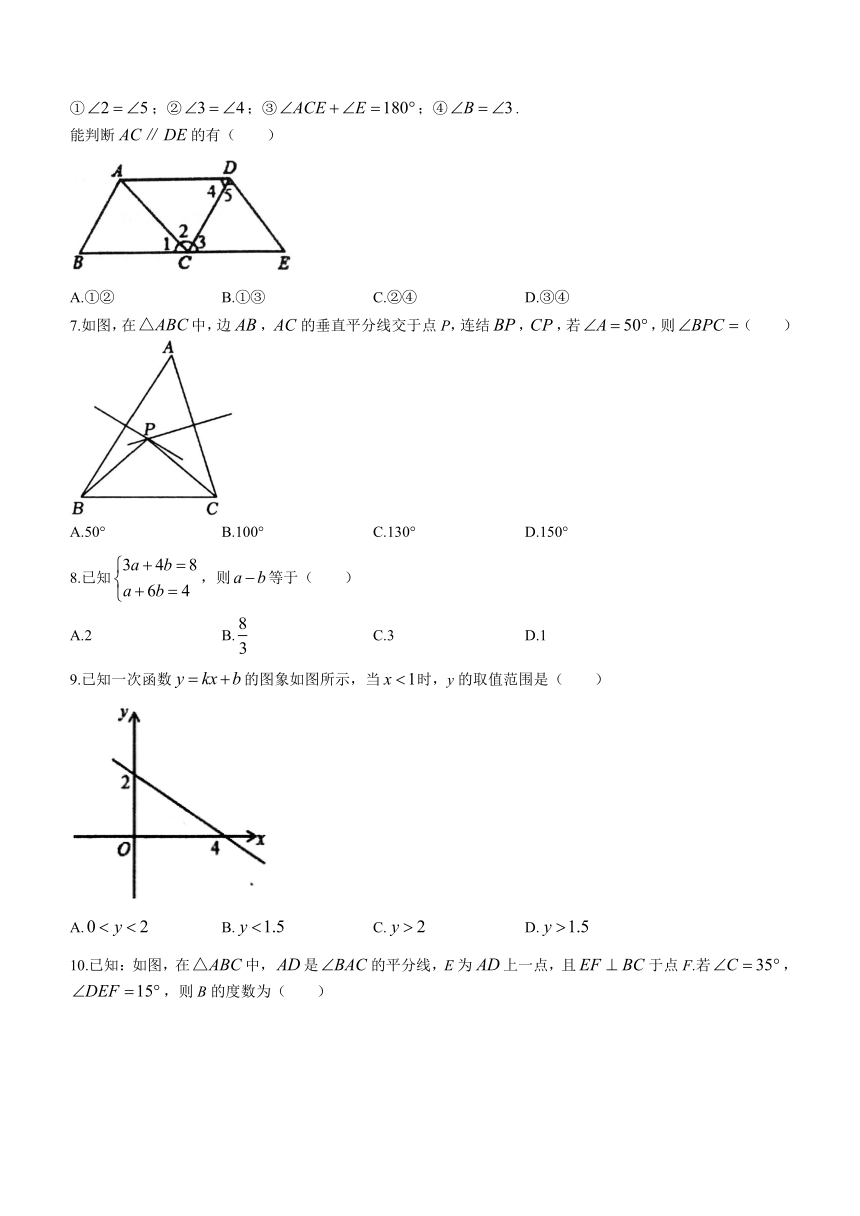
6.如图,点E在的延长线上,下列条件中,
①;②;③;④.
能判断的有( )
A.①② B.①③ C.②④ D.③④
7.如图,在中,边,的垂直平分线交于点P,连结,,若,则( )
A.50° B.100° C.130° D.150°
8.已知,则等于( )
A.2 B. C.3 D.1
9.已知一次函数的图象如图所示,当时,y的取值范围是( )
A. B. C. D.
10.已知:如图,在中,是的平分线,E为上一点,且于点F.若,,则B的度数为( )
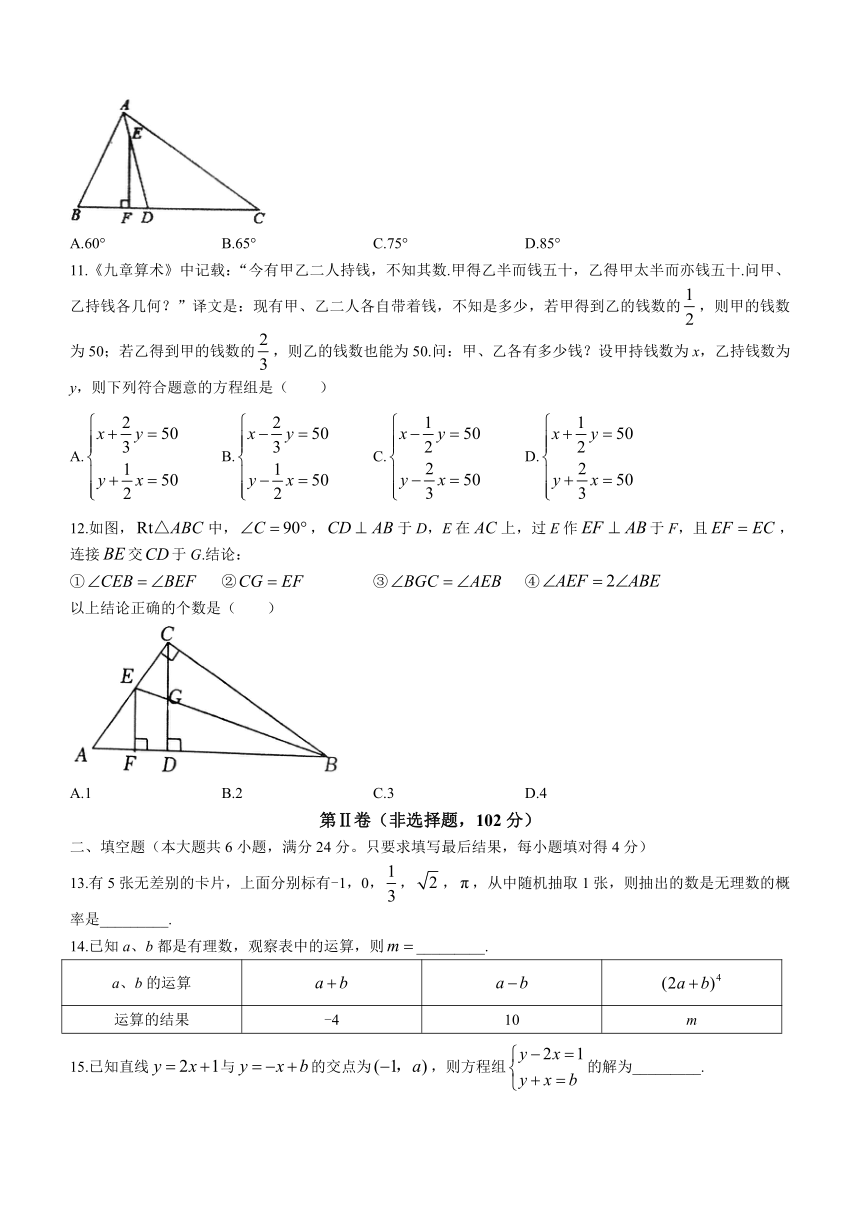
A.60° B.65° C.75° D.85°
11.《九章算术》中记载:“今有甲乙二人持钱,不知其数.甲得乙半而钱五十,乙得甲太半而亦钱五十.问甲、乙持钱各几何?”译文是:现有甲、乙二人各自带着钱,不知是多少,若甲得到乙的钱数的,则甲的钱数为50;若乙得到甲的钱数的,则乙的钱数也能为50.问:甲、乙各有多少钱?设甲持钱数为x,乙持钱数为y,则下列符合题意的方程组是( )
A. B. C. D.
12.如图,中,,于D,E在上,过E作于F,且,连接交于G.结论:
① ② ③ ④
以上结论正确的个数是( )
A.1 B.2 C.3 D.4
第Ⅱ卷(非选择题,102分)
二、填空题(本大题共6小题,满分24分。只要求填写最后结果,每小题填对得4分)
13.有5张无差别的卡片,上面分别标有-1,0,,,,从中随机抽取1张,则抽出的数是无理数的概率是_________.
14.已知a、b都是有理数,观察表中的运算,则_________.
a、b的运算
运算的结果 -4 10 m
15.已知直线与的交点为,则方程组的解为_________.
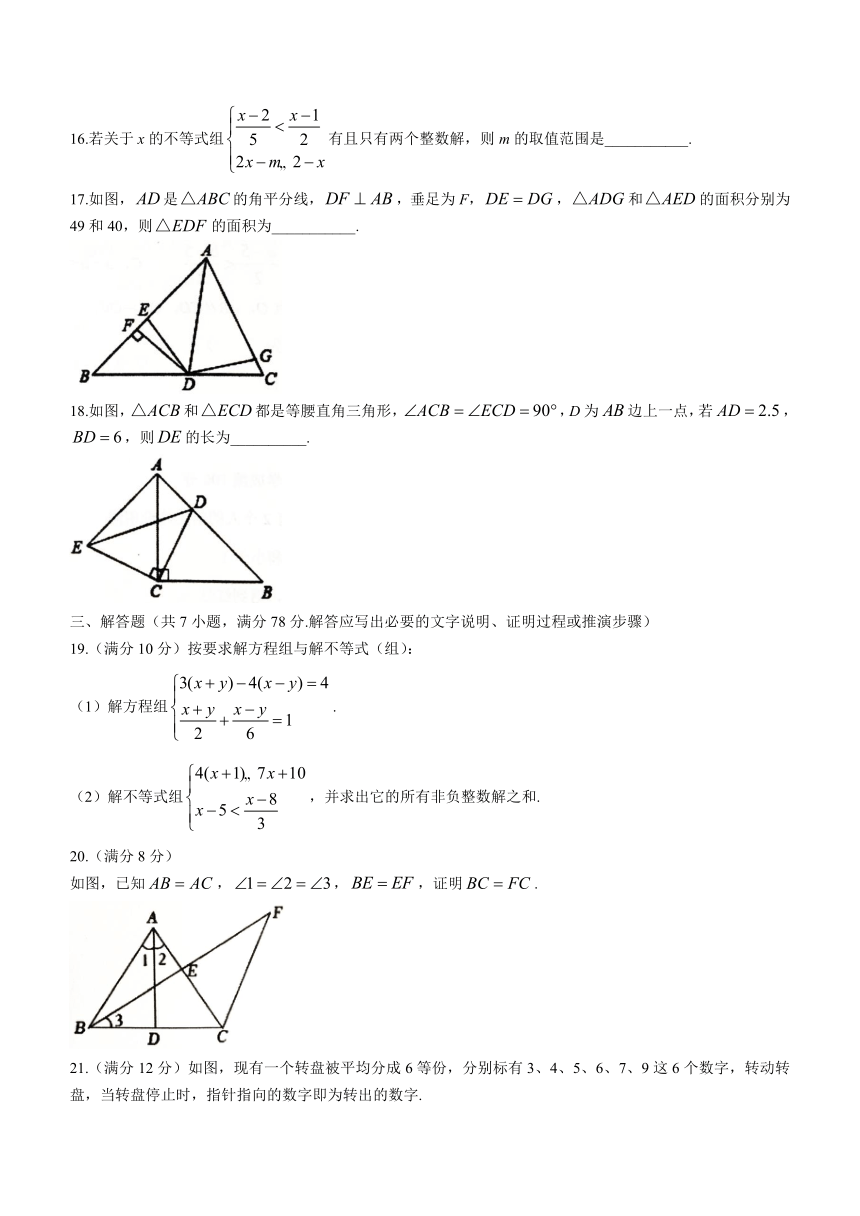
16.若关于x的不等式组有且只有两个整数解,则m的取值范围是___________.
17.如图,是的角平分线,,垂足为F,,和的面积分别为49和40,则的面积为___________.
18.如图,和都是等腰直角三角形,,D为边上一点,若,,则的长为__________.
三、解答题(共7小题,满分78分.解答应写出必要的文字说明、证明过程或推演步骤)
19.(满分10分)按要求解方程组与解不等式(组):
(1)解方程组.
(2)解不等式组,并求出它的所有非负整数解之和.
20.(满分8分)
如图,已知,,,证明.
21.(满分12分)如图,现有一个转盘被平均分成6等份,分别标有3、4、5、6、7、9这6个数字,转动转盘,当转盘停止时,指针指向的数字即为转出的数字.
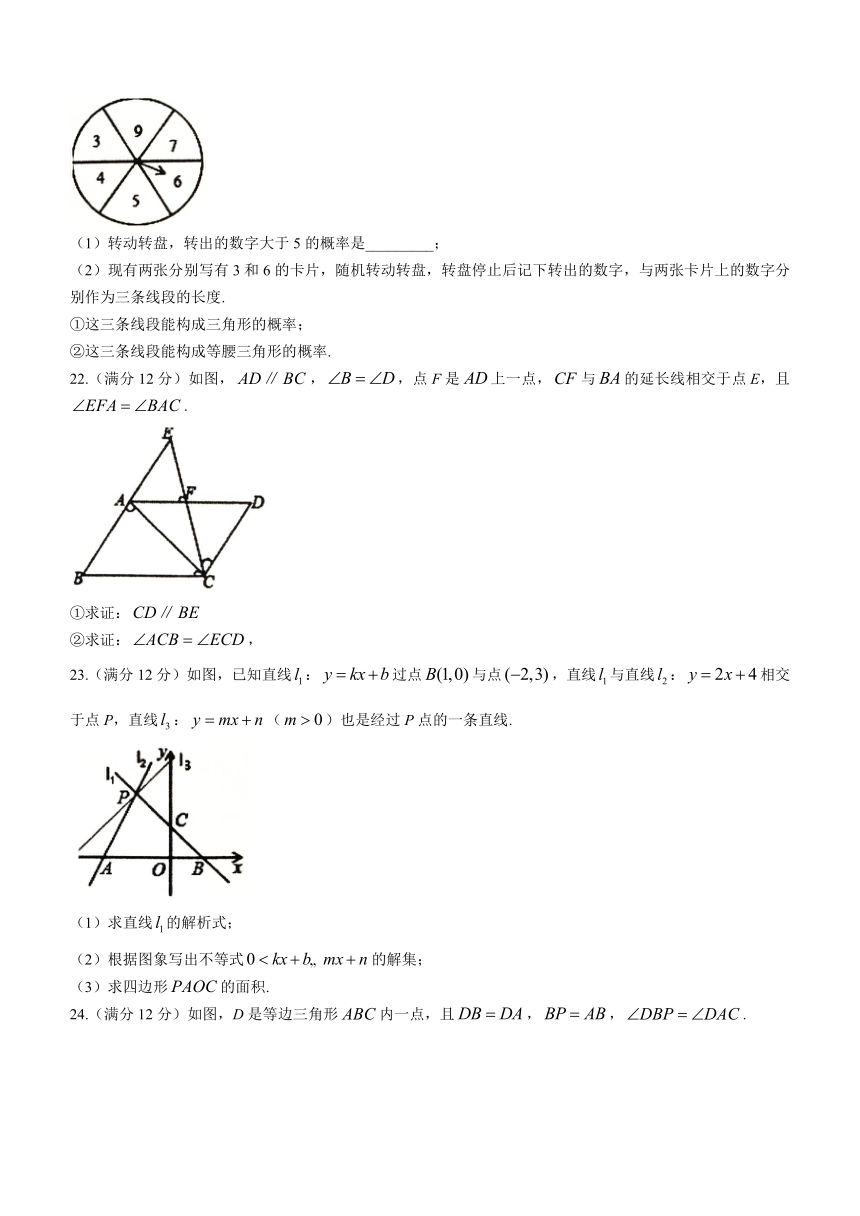
(1)转动转盘,转出的数字大于5的概率是_________;
(2)现有两张分别写有3和6的卡片,随机转动转盘,转盘停止后记下转出的数字,与两张卡片上的数字分别作为三条线段的长度.
①这三条线段能构成三角形的概率;
②这三条线段能构成等腰三角形的概率.
22.(满分12分)如图,,,点F是上一点,与的延长线相交于点E,且.
①求证:
②求证:,
23.(满分12分)如图,已知直线:过点与点,直线与直线:相交于点P,直线:()也是经过P点的一条直线.
(1)求直线的解析式;
(2)根据图象写出不等式的解集;
(3)求四边形的面积.
24.(满分12分)如图,D是等边三角形内一点,且,,.
①求证:
②求的度数
25.(满分12分)又是一年毕业季,学校外一超市推出甲、乙两种可以免费印制logo的毕业纪念品。该超市需要购进甲、乙两种纪念品共160件,其进价和售价如下表:(注:获利=售价-进价)
甲 乙
进价(元/件) 15 35
售价(元/件) 20 45
(1)若超市计划销售完这批纪念品后能获利1100元,问甲、乙两种纪念品应分别购进多少件?
(2)若超市计划投入资金不超过4290元,且销售完这批纪念品后获利不低于1260元,请问共有几种购货方案?哪种方案使得全部销售完这批纪念品后获利最大?获利最大是多少?
2021-2022学年下学期初二数学
期末练习题答案
(考试时间120分钟,满分150分)
本试题分Ⅰ、Ⅱ卷,第Ⅰ卷为选择题,48分;第Ⅱ卷为非选择题,102分。全卷满分150分。
第Ⅰ卷(选择题)
一、选择题(本大题共12小题,在每小题给出的四个选项中,只有一个是正确的,请把正确的选项选出来,每小题选对得4分,错选、不选或选出的答案超过一个,均记零分)
题号 1 2 3 4 5 6 7 8 9 10 11 12
答案 C B C C D B B A D B D D
第Ⅱ卷(非选择题,102分)
一、填空题(本大题共6小题,满分24分。只要求填写最后结果,每小题填对得4分)
13. 14.1 15. 16. 17.4.5 18.6.5
三、解答题(共7小题,满分78分.解答应写出必要的文字说明、证明过程或推演步骤)
19.(满分10分)
(1)原方程组去分母,去括号得:
.
①②得:.
∴.
代入②得:.
∴原方程组的解为:. 5
(2)解:,
∵解不等式①得:,
解不等式②得:,
∴不等式组的解集为, 3
∴不等式组的非负整数解为0,1,2,3;
∵,
∴原不等式组的所有非负整数解之和为6. 5
20.(满分8分)
解:∵,,
∴(三线合一),
∴(垂直的意义),2
∵,(三角形内角和定理),
∴, 4
又(已知),
∴(等式性质),
∵(邻补角的意义),
∴(等式性质), 6
∴(等量代换),
在与中,
,
∴,
∴(全等三角形的对应边相等). 8
21.(满分12分)
解:(1)转盘被平均分成6等份,转到每个数字的可能性相等,共有6种可能结果,大于5的结果有3种,
∴转出的数字大于5的概率是. 4
故答案为:;
(2)①转盘被平均分成6等份,转到每个数字的可能性相等,共有6种可能结果,能构成三角形的结果有4种,
∴这三条线段能构成三角形的概率是; 8
②转盘被平均分成6等份,转到每个数字的可能性相等,共有6种可能结果,能构成等腰三角形的结果有1种,
∴这三条线段能构成等腰三角形的概率是.
故答案为:. 12
22.(满分12分)
证明:∵,
∴
又∵
∴
∴ 5
∵,
∴,
∵
∴,
∵
∴,
即. 12
23.(满分12分)
解:(1)∵直线:过点与点,
∴,
解得.
∴直线的解析式为:
∵点P是直线:与直线:的交点
∴
解得. 5
∴不等式的解集. 8
(3)∵直线与y轴相交于点C,
∴C的坐标为,
又∵直线与x轴相交于点A,
∴A点的坐标为,则,
而,
∴. 12
24.(满分12分)
(1)解:∵是等边三角形,
∴,
∵
∴
又∵,.
∴ 3
∴
∴
即 6
(2)∵是等边三角形,
∴,.
在和中,
,
∴, 9
∴.
∵,
∴.
∵,
∴. 12
25.(满分12分)
解:(1)设甲种纪念品应购进x件,乙种纪念品应购进y件.
根据题意得:,
解得:. 4
答:甲种纪念品购进100件,乙种纪念品购进60件.5
(2)设甲种纪念品购进a件,则乙种纪念品购进件.
根据题意得:, 8
解得:.
∵a为非负整数,
∴a取66,67,689
∴相应取94,93,92. 10
设销售完这批纪念品获利为w
则
∴w随a增大而减小
∴当时,w最大,最大为1270元 12
初二数学练习题
(考试时间120分钟,满分150分)
本试题分Ⅰ、Ⅱ卷,第Ⅰ卷为选择题,48分;第Ⅱ卷为非选择题,102分。全卷满分150分。
第Ⅰ卷(选择题)
一、选择题(本大题共12小题,在每小题给出的四个选项中,只有一个是正确的,请把正确的选项选出来,每小题选对得4分,错选、不选或选出的答案超过一个,均记零分)
1.下列命题中,真命题是( )
A.两条直线被第三条直线所截,同位角相等
B.等腰三角形的高线、中线、角平分线互相重合
C.在同一平面内,过一点有且只有一条直线与已知直线垂直
D.若,则且
2.已知,则下列不等式中错误的是( )
A. B. C. D.
3.如图,已知交于点O,,,,则的大小为( )
A.10° B.15° C.25° D.30°
4.下列事件中属于不可能事件的是( )
A.数学测验中,小明数学成绩100分
B.任选13个人,至少有2个人的出生月份相同
C.任取两个正整数,其和小于1
D.乘公交车到十字路口,遇到红灯
5.一只苍蝇飞到如图所示的一面墙上,最终停在白色区域上的概率是( )
A. B. C. D.
6.如图,点E在的延长线上,下列条件中,
①;②;③;④.
能判断的有( )
A.①② B.①③ C.②④ D.③④
7.如图,在中,边,的垂直平分线交于点P,连结,,若,则( )
A.50° B.100° C.130° D.150°
8.已知,则等于( )
A.2 B. C.3 D.1
9.已知一次函数的图象如图所示,当时,y的取值范围是( )
A. B. C. D.
10.已知:如图,在中,是的平分线,E为上一点,且于点F.若,,则B的度数为( )
A.60° B.65° C.75° D.85°
11.《九章算术》中记载:“今有甲乙二人持钱,不知其数.甲得乙半而钱五十,乙得甲太半而亦钱五十.问甲、乙持钱各几何?”译文是:现有甲、乙二人各自带着钱,不知是多少,若甲得到乙的钱数的,则甲的钱数为50;若乙得到甲的钱数的,则乙的钱数也能为50.问:甲、乙各有多少钱?设甲持钱数为x,乙持钱数为y,则下列符合题意的方程组是( )
A. B. C. D.
12.如图,中,,于D,E在上,过E作于F,且,连接交于G.结论:
① ② ③ ④
以上结论正确的个数是( )
A.1 B.2 C.3 D.4
第Ⅱ卷(非选择题,102分)
二、填空题(本大题共6小题,满分24分。只要求填写最后结果,每小题填对得4分)
13.有5张无差别的卡片,上面分别标有-1,0,,,,从中随机抽取1张,则抽出的数是无理数的概率是_________.
14.已知a、b都是有理数,观察表中的运算,则_________.
a、b的运算
运算的结果 -4 10 m
15.已知直线与的交点为,则方程组的解为_________.
16.若关于x的不等式组有且只有两个整数解,则m的取值范围是___________.
17.如图,是的角平分线,,垂足为F,,和的面积分别为49和40,则的面积为___________.
18.如图,和都是等腰直角三角形,,D为边上一点,若,,则的长为__________.
三、解答题(共7小题,满分78分.解答应写出必要的文字说明、证明过程或推演步骤)
19.(满分10分)按要求解方程组与解不等式(组):
(1)解方程组.
(2)解不等式组,并求出它的所有非负整数解之和.
20.(满分8分)
如图,已知,,,证明.
21.(满分12分)如图,现有一个转盘被平均分成6等份,分别标有3、4、5、6、7、9这6个数字,转动转盘,当转盘停止时,指针指向的数字即为转出的数字.
(1)转动转盘,转出的数字大于5的概率是_________;
(2)现有两张分别写有3和6的卡片,随机转动转盘,转盘停止后记下转出的数字,与两张卡片上的数字分别作为三条线段的长度.
①这三条线段能构成三角形的概率;
②这三条线段能构成等腰三角形的概率.
22.(满分12分)如图,,,点F是上一点,与的延长线相交于点E,且.
①求证:
②求证:,
23.(满分12分)如图,已知直线:过点与点,直线与直线:相交于点P,直线:()也是经过P点的一条直线.
(1)求直线的解析式;
(2)根据图象写出不等式的解集;
(3)求四边形的面积.
24.(满分12分)如图,D是等边三角形内一点,且,,.
①求证:
②求的度数
25.(满分12分)又是一年毕业季,学校外一超市推出甲、乙两种可以免费印制logo的毕业纪念品。该超市需要购进甲、乙两种纪念品共160件,其进价和售价如下表:(注:获利=售价-进价)
甲 乙
进价(元/件) 15 35
售价(元/件) 20 45
(1)若超市计划销售完这批纪念品后能获利1100元,问甲、乙两种纪念品应分别购进多少件?
(2)若超市计划投入资金不超过4290元,且销售完这批纪念品后获利不低于1260元,请问共有几种购货方案?哪种方案使得全部销售完这批纪念品后获利最大?获利最大是多少?
2021-2022学年下学期初二数学
期末练习题答案
(考试时间120分钟,满分150分)
本试题分Ⅰ、Ⅱ卷,第Ⅰ卷为选择题,48分;第Ⅱ卷为非选择题,102分。全卷满分150分。
第Ⅰ卷(选择题)
一、选择题(本大题共12小题,在每小题给出的四个选项中,只有一个是正确的,请把正确的选项选出来,每小题选对得4分,错选、不选或选出的答案超过一个,均记零分)
题号 1 2 3 4 5 6 7 8 9 10 11 12
答案 C B C C D B B A D B D D
第Ⅱ卷(非选择题,102分)
一、填空题(本大题共6小题,满分24分。只要求填写最后结果,每小题填对得4分)
13. 14.1 15. 16. 17.4.5 18.6.5
三、解答题(共7小题,满分78分.解答应写出必要的文字说明、证明过程或推演步骤)
19.(满分10分)
(1)原方程组去分母,去括号得:
.
①②得:.
∴.
代入②得:.
∴原方程组的解为:. 5
(2)解:,
∵解不等式①得:,
解不等式②得:,
∴不等式组的解集为, 3
∴不等式组的非负整数解为0,1,2,3;
∵,
∴原不等式组的所有非负整数解之和为6. 5
20.(满分8分)
解:∵,,
∴(三线合一),
∴(垂直的意义),2
∵,(三角形内角和定理),
∴, 4
又(已知),
∴(等式性质),
∵(邻补角的意义),
∴(等式性质), 6
∴(等量代换),
在与中,
,
∴,
∴(全等三角形的对应边相等). 8
21.(满分12分)
解:(1)转盘被平均分成6等份,转到每个数字的可能性相等,共有6种可能结果,大于5的结果有3种,
∴转出的数字大于5的概率是. 4
故答案为:;
(2)①转盘被平均分成6等份,转到每个数字的可能性相等,共有6种可能结果,能构成三角形的结果有4种,
∴这三条线段能构成三角形的概率是; 8
②转盘被平均分成6等份,转到每个数字的可能性相等,共有6种可能结果,能构成等腰三角形的结果有1种,
∴这三条线段能构成等腰三角形的概率是.
故答案为:. 12
22.(满分12分)
证明:∵,
∴
又∵
∴
∴ 5
∵,
∴,
∵
∴,
∵
∴,
即. 12
23.(满分12分)
解:(1)∵直线:过点与点,
∴,
解得.
∴直线的解析式为:
∵点P是直线:与直线:的交点
∴
解得. 5
∴不等式的解集. 8
(3)∵直线与y轴相交于点C,
∴C的坐标为,
又∵直线与x轴相交于点A,
∴A点的坐标为,则,
而,
∴. 12
24.(满分12分)
(1)解:∵是等边三角形,
∴,
∵
∴
又∵,.
∴ 3
∴
∴
即 6
(2)∵是等边三角形,
∴,.
在和中,
,
∴, 9
∴.
∵,
∴.
∵,
∴. 12
25.(满分12分)
解:(1)设甲种纪念品应购进x件,乙种纪念品应购进y件.
根据题意得:,
解得:. 4
答:甲种纪念品购进100件,乙种纪念品购进60件.5
(2)设甲种纪念品购进a件,则乙种纪念品购进件.
根据题意得:, 8
解得:.
∵a为非负整数,
∴a取66,67,689
∴相应取94,93,92. 10
设销售完这批纪念品获利为w
则
∴w随a增大而减小
∴当时,w最大,最大为1270元 12
同课章节目录
