北师大版九年级下册 1.4 解直角三角形 课件(共25张PPT)
文档属性
| 名称 | 北师大版九年级下册 1.4 解直角三角形 课件(共25张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 447.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-07-07 16:49:39 | ||
图片预览


文档简介
(共25张PPT)
第1章 直角三角形的边角关系
1.4 解直角三角形
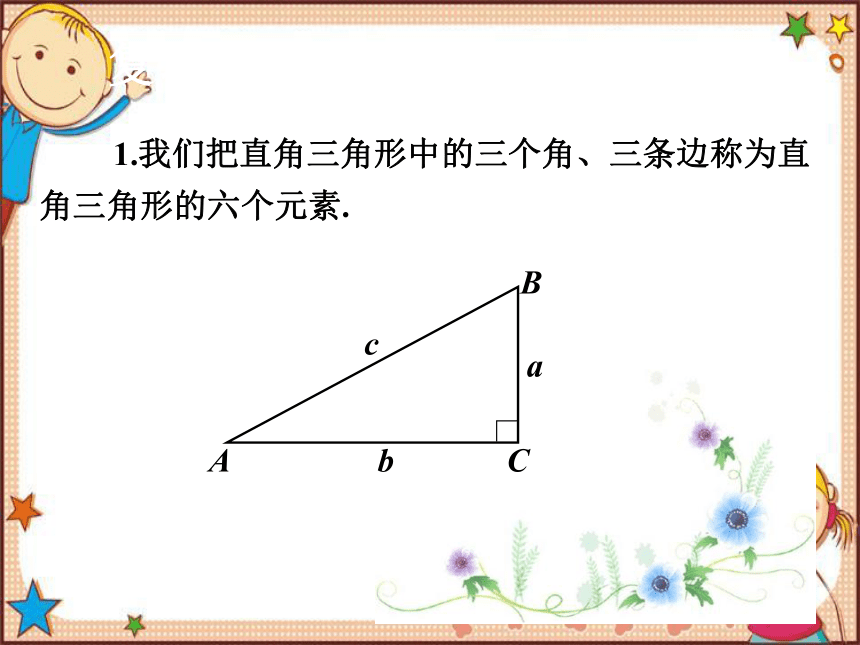
1.我们把直角三角形中的三个角、三条边称为直角三角形的六个元素.
复习回顾
A
B
C
a
b
c
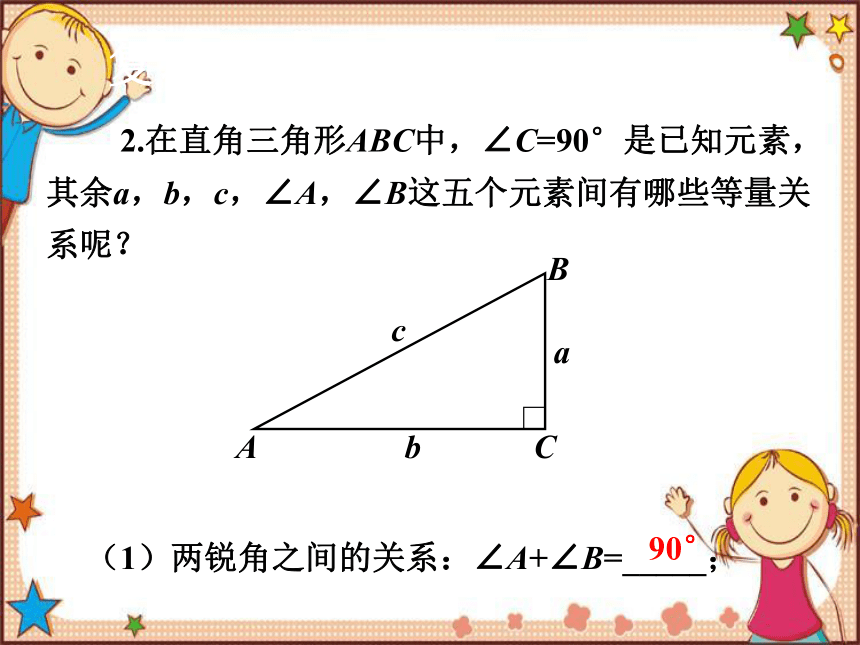
2.在直角三角形ABC中,∠C=90°是已知元素,其余a,b,c,∠A,∠B这五个元素间有哪些等量关系呢?
(1)两锐角之间的关系:∠A+∠B=_____;
复习回顾
A
B
C
a
b
c
90°
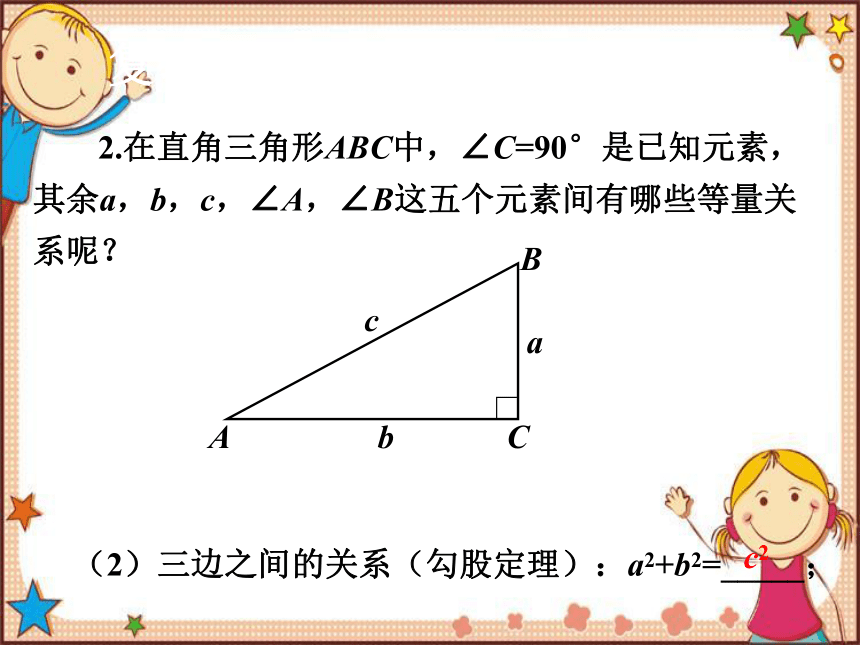
2.在直角三角形ABC中,∠C=90°是已知元素,其余a,b,c,∠A,∠B这五个元素间有哪些等量关系呢?
(2)三边之间的关系(勾股定理):a2+b2=_____;
复习回顾
A
B
C
a
b
c
c2
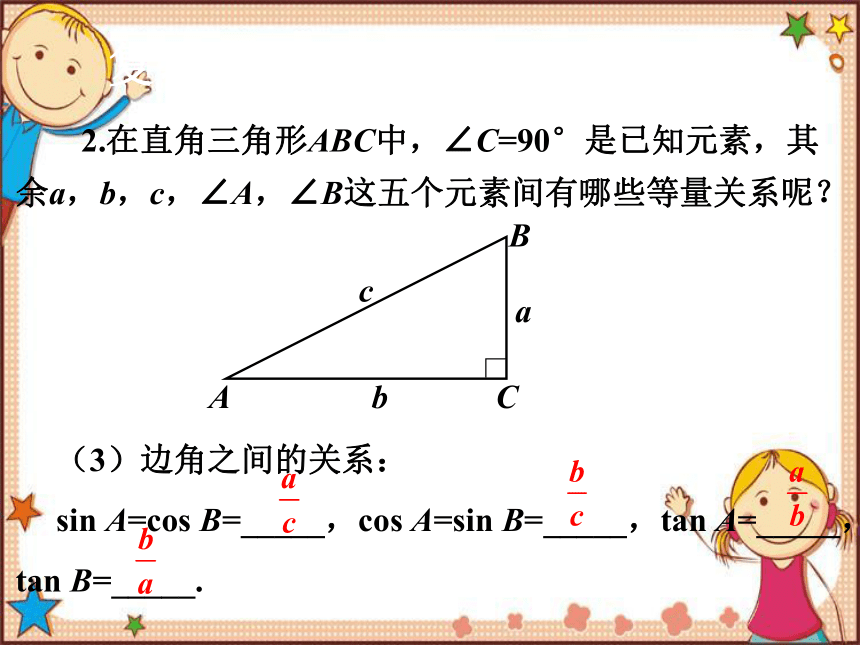
2.在直角三角形ABC中,∠C=90°是已知元素,其余a,b,c,∠A,∠B这五个元素间有哪些等量关系呢?
(3)边角之间的关系:
sin A=cos B=_____,cos A=sin B=_____,tan A=_____,tan B=_____.
复习回顾
A
B
C
a
b
c
解直角三角形的概念是:由直角三角形中的已知元素求出所有未知元素的过程.
讲授新课
解直角三角形的方法:利用直角三角形两锐角之间的关系、三边之间的关系、边角之间的关系解决问题.
讲授新课
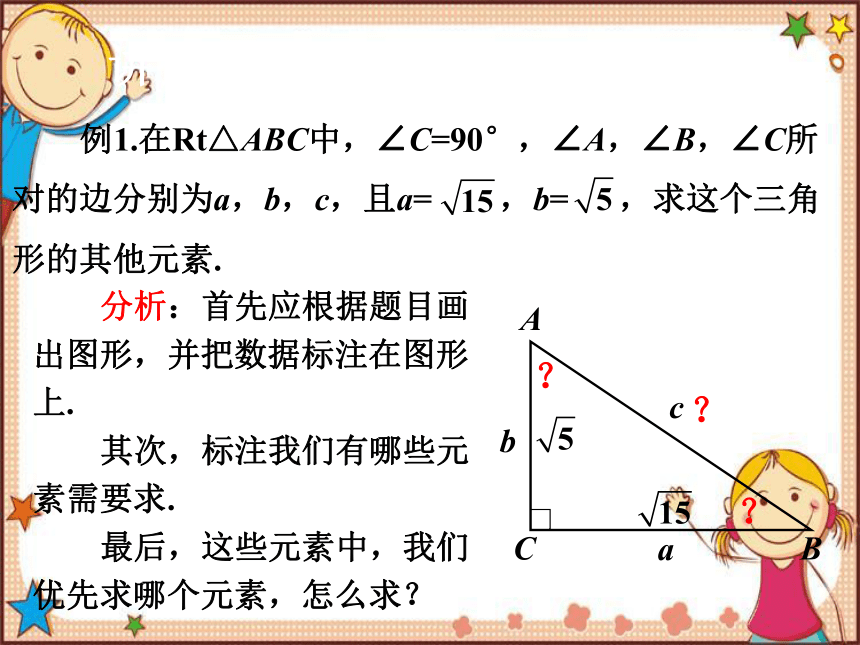
例1.在Rt△ABC中,∠C=90°,∠A,∠B,∠C所对的边分别为a,b,c,且a= ,b= ,求这个三角形的其他元素.
C
A
B
a
b
c
?
?
?
分析:首先应根据题目画出图形,并把数据标注在图形上.
其次,标注我们有哪些元素需要求.
最后,这些元素中,我们优先求哪个元素,怎么求?
讲授新课
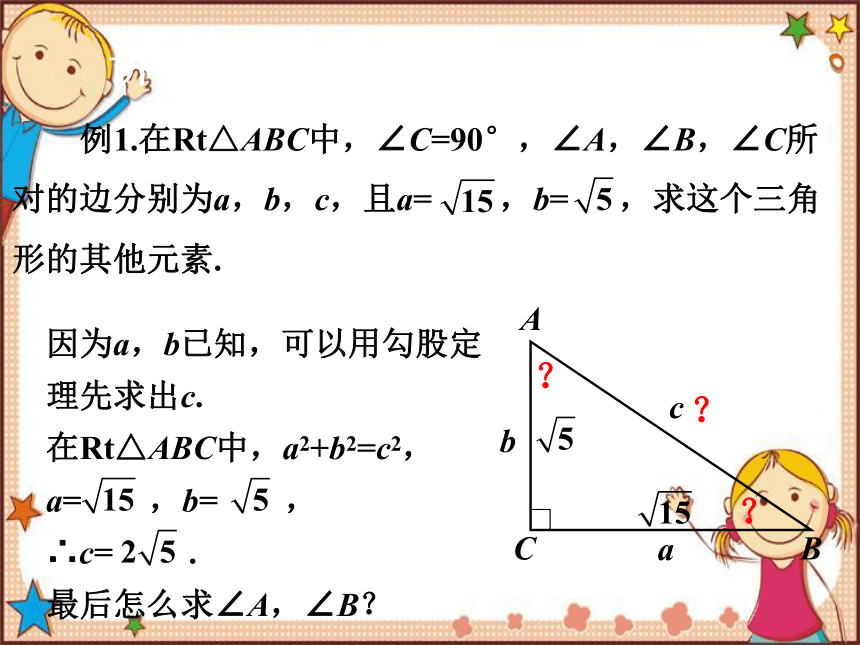
例1.在Rt△ABC中,∠C=90°,∠A,∠B,∠C所对的边分别为a,b,c,且a= ,b= ,求这个三角形的其他元素.
C
A
B
a
b
c
?
?
?
因为a,b已知,可以用勾股定理先求出c.
在Rt△ABC中,a2+b2=c2,a= ,b= ,
∴c= .
最后怎么求∠A,∠B?
讲授新课
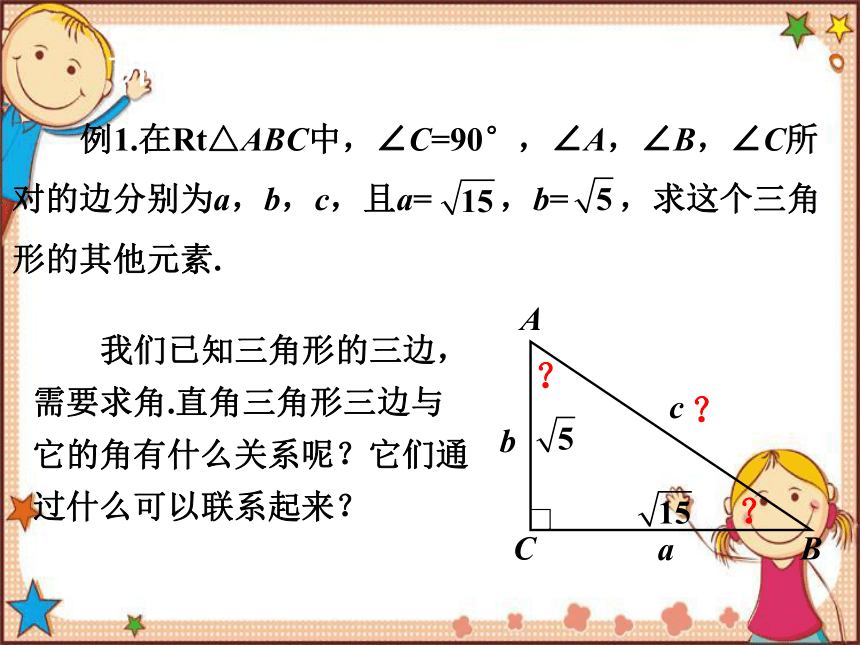
例1.在Rt△ABC中,∠C=90°,∠A,∠B,∠C所对的边分别为a,b,c,且a= ,b= ,求这个三角形的其他元素.
C
A
B
a
b
c
?
?
?
我们已知三角形的三边,需要求角.直角三角形三边与它的角有什么关系呢?它们通过什么可以联系起来?
讲授新课
例1.在Rt△ABC中,∠C=90°,∠A,∠B,∠C所对的边分别为a,b,c,且a= ,b= ,求这个三角形的其他元素.
C
A
B
a
b
c
?
?
?
在Rt△ABC中,
∴∠B= 30°,∴∠ A = 60°.
思考1:为什么选择 呢?还可以选择其他三角函数吗?试一试?
讲授新课
小结:
(1)选择比值分母中不含根式的三角函数.
(2)选择比值化简过程较为简单的三角函数.
C
A
B
a
b
c
?
?
?
思考2:上述例1中,我们已知两直角边,如果已知的是一直角边与斜边,解题过程有什么变化吗?请找出最优解题方式.
讲授新课
C
A
B
a
b
c
?
?
?
解:在Rt△ABC中,a2+b2=c2,a= ,c= ,
∴b= .
∴∠B= 30°,∴∠ A = 60°.
思考3:上述例1中,已知两边,我们能够解直角三角形,那么已知一边一角(除直角外的角)能解直角三角形吗?
讲授新课
例2.在Rt△ABC中,∠C=90°,∠A,∠B,∠C所对的边分别为a,b,c,且b=30,∠B=25°,求这个三角形的其他元素(边长精确到1).
讲授新课
C
A
B
a
b
c
30
?
?
?
25°
解:在Rt△ABC中, ∠C=90°, ∠B=25° ,∴ ∠A=65°.
思考4:例2中已知元素是一锐角与一直角边,如果已知的是一锐角与斜边,能解直角三角形吗?
讲授新课
C
A
B
a
b
c
71
?
?
?
25°
解:在Rt△ABC中, ∠C=90°, ∠B=25°,∴ ∠A=65°.
思考5:已知元素是两锐角,能解直角三角形吗?
讲授新课
小结:解直角三角形最少需除直角外的两个元素,且这两个元素中至少有一条边.
C
A
B
a
b
c
?
?
?
25°
65°
随堂练习
在Rt△ABC中, ∠C=90°, ∠A,∠B,∠C所对的边分别为a,b,c,根据下列条件求出直角三角形的其他元素(结果精确到1°):
巩固练习
(1)已知a=4,b=8;
(2)已知b=10, ∠B=60°;
(3)已知c=20, ∠A=60°.
随堂练习
在Rt△ABC中, ∠C=90°, ∠A,∠B,∠C所对的边分别为a,b,c,根据下列条件求出直角三角形的其他元素(结果精确到1°):
巩固练习
(1)已知a=4,b=8;
解:∠A≈27°, ∠B ≈ 63°,
c=
C
B
A
a
b
c
随堂练习
在Rt△ABC中, ∠C=90°, ∠A,∠B,∠C所对的边分别为a,b,c,根据下列条件求出直角三角形的其他元素(结果精确到1°):
巩固练习
(2)已知b=10, ∠B=60°;
C
B
A
a
b
c
解:∠A=30°,
a= ,c=
随堂练习
在Rt△ABC中, ∠C=90°, ∠A,∠B,∠C所对的边分别为a,b,c,根据下列条件求出直角三角形的其他元素(结果精确到1°):
巩固练习
(3)已知c=20, ∠A=60°.
C
B
A
a
b
c
解:∠B=30°, b=10,
a=
如何灵活应用各个关系式快速解直角三角形?
探究拓展
A
C
B
b
a
c
探究拓展
已知条件 解法
一边一角 已知斜边c和一个锐角A
已知一条直角边a和一个锐角A
两边 已知斜边c和一条直角边a
已知两条直角边a,b
小结:可以用以下口诀帮助记忆.
已知斜边求直边,正弦余弦很方便;
已知直边求直边,正切余切理当然;
已知两边求一边,勾股定理最方便;
已知两边求一角,函数关系要选好;
已知锐角求锐角,互余关系要记好;
已知直边求斜边,用除还需正余弦,
计算方法要选择,能用乘法不用除.
探究拓展
教材第17~18页习题1.5第1~4题.
布置作业
谢谢大家!
再见!
第1章 直角三角形的边角关系
1.4 解直角三角形
1.我们把直角三角形中的三个角、三条边称为直角三角形的六个元素.
复习回顾
A
B
C
a
b
c
2.在直角三角形ABC中,∠C=90°是已知元素,其余a,b,c,∠A,∠B这五个元素间有哪些等量关系呢?
(1)两锐角之间的关系:∠A+∠B=_____;
复习回顾
A
B
C
a
b
c
90°
2.在直角三角形ABC中,∠C=90°是已知元素,其余a,b,c,∠A,∠B这五个元素间有哪些等量关系呢?
(2)三边之间的关系(勾股定理):a2+b2=_____;
复习回顾
A
B
C
a
b
c
c2
2.在直角三角形ABC中,∠C=90°是已知元素,其余a,b,c,∠A,∠B这五个元素间有哪些等量关系呢?
(3)边角之间的关系:
sin A=cos B=_____,cos A=sin B=_____,tan A=_____,tan B=_____.
复习回顾
A
B
C
a
b
c
解直角三角形的概念是:由直角三角形中的已知元素求出所有未知元素的过程.
讲授新课
解直角三角形的方法:利用直角三角形两锐角之间的关系、三边之间的关系、边角之间的关系解决问题.
讲授新课
例1.在Rt△ABC中,∠C=90°,∠A,∠B,∠C所对的边分别为a,b,c,且a= ,b= ,求这个三角形的其他元素.
C
A
B
a
b
c
?
?
?
分析:首先应根据题目画出图形,并把数据标注在图形上.
其次,标注我们有哪些元素需要求.
最后,这些元素中,我们优先求哪个元素,怎么求?
讲授新课
例1.在Rt△ABC中,∠C=90°,∠A,∠B,∠C所对的边分别为a,b,c,且a= ,b= ,求这个三角形的其他元素.
C
A
B
a
b
c
?
?
?
因为a,b已知,可以用勾股定理先求出c.
在Rt△ABC中,a2+b2=c2,a= ,b= ,
∴c= .
最后怎么求∠A,∠B?
讲授新课
例1.在Rt△ABC中,∠C=90°,∠A,∠B,∠C所对的边分别为a,b,c,且a= ,b= ,求这个三角形的其他元素.
C
A
B
a
b
c
?
?
?
我们已知三角形的三边,需要求角.直角三角形三边与它的角有什么关系呢?它们通过什么可以联系起来?
讲授新课
例1.在Rt△ABC中,∠C=90°,∠A,∠B,∠C所对的边分别为a,b,c,且a= ,b= ,求这个三角形的其他元素.
C
A
B
a
b
c
?
?
?
在Rt△ABC中,
∴∠B= 30°,∴∠ A = 60°.
思考1:为什么选择 呢?还可以选择其他三角函数吗?试一试?
讲授新课
小结:
(1)选择比值分母中不含根式的三角函数.
(2)选择比值化简过程较为简单的三角函数.
C
A
B
a
b
c
?
?
?
思考2:上述例1中,我们已知两直角边,如果已知的是一直角边与斜边,解题过程有什么变化吗?请找出最优解题方式.
讲授新课
C
A
B
a
b
c
?
?
?
解:在Rt△ABC中,a2+b2=c2,a= ,c= ,
∴b= .
∴∠B= 30°,∴∠ A = 60°.
思考3:上述例1中,已知两边,我们能够解直角三角形,那么已知一边一角(除直角外的角)能解直角三角形吗?
讲授新课
例2.在Rt△ABC中,∠C=90°,∠A,∠B,∠C所对的边分别为a,b,c,且b=30,∠B=25°,求这个三角形的其他元素(边长精确到1).
讲授新课
C
A
B
a
b
c
30
?
?
?
25°
解:在Rt△ABC中, ∠C=90°, ∠B=25° ,∴ ∠A=65°.
思考4:例2中已知元素是一锐角与一直角边,如果已知的是一锐角与斜边,能解直角三角形吗?
讲授新课
C
A
B
a
b
c
71
?
?
?
25°
解:在Rt△ABC中, ∠C=90°, ∠B=25°,∴ ∠A=65°.
思考5:已知元素是两锐角,能解直角三角形吗?
讲授新课
小结:解直角三角形最少需除直角外的两个元素,且这两个元素中至少有一条边.
C
A
B
a
b
c
?
?
?
25°
65°
随堂练习
在Rt△ABC中, ∠C=90°, ∠A,∠B,∠C所对的边分别为a,b,c,根据下列条件求出直角三角形的其他元素(结果精确到1°):
巩固练习
(1)已知a=4,b=8;
(2)已知b=10, ∠B=60°;
(3)已知c=20, ∠A=60°.
随堂练习
在Rt△ABC中, ∠C=90°, ∠A,∠B,∠C所对的边分别为a,b,c,根据下列条件求出直角三角形的其他元素(结果精确到1°):
巩固练习
(1)已知a=4,b=8;
解:∠A≈27°, ∠B ≈ 63°,
c=
C
B
A
a
b
c
随堂练习
在Rt△ABC中, ∠C=90°, ∠A,∠B,∠C所对的边分别为a,b,c,根据下列条件求出直角三角形的其他元素(结果精确到1°):
巩固练习
(2)已知b=10, ∠B=60°;
C
B
A
a
b
c
解:∠A=30°,
a= ,c=
随堂练习
在Rt△ABC中, ∠C=90°, ∠A,∠B,∠C所对的边分别为a,b,c,根据下列条件求出直角三角形的其他元素(结果精确到1°):
巩固练习
(3)已知c=20, ∠A=60°.
C
B
A
a
b
c
解:∠B=30°, b=10,
a=
如何灵活应用各个关系式快速解直角三角形?
探究拓展
A
C
B
b
a
c
探究拓展
已知条件 解法
一边一角 已知斜边c和一个锐角A
已知一条直角边a和一个锐角A
两边 已知斜边c和一条直角边a
已知两条直角边a,b
小结:可以用以下口诀帮助记忆.
已知斜边求直边,正弦余弦很方便;
已知直边求直边,正切余切理当然;
已知两边求一边,勾股定理最方便;
已知两边求一角,函数关系要选好;
已知锐角求锐角,互余关系要记好;
已知直边求斜边,用除还需正余弦,
计算方法要选择,能用乘法不用除.
探究拓展
教材第17~18页习题1.5第1~4题.
布置作业
谢谢大家!
再见!
