13.1.2 线段的垂直平分线的性质(第二课时) 课件(共17张PPT)
文档属性
| 名称 | 13.1.2 线段的垂直平分线的性质(第二课时) 课件(共17张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 5.6MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-07-07 06:21:35 | ||
图片预览






文档简介
(共17张PPT)
第13.1.2线段的垂直平分线的性质
(第二课时)
人教版数学八年级上册
学习目标
1、掌握线段垂直平分线的画法.
2、能正确找出轴对称图形的对称轴.
3、熟练运用线段垂直平分线的性质和判定解决实际问题.
情境引入
同学们,还记得我们上节课学习的线段的垂直平分线的性质和判定吗?.
线段垂直平分线上的点与这条线段两个端点的距离相等.
线段的垂直平分线的性质:
与线段两个端点距离相等的点在这条线段的垂直平分线上.
线段的垂直平分线的判定:
情境引入
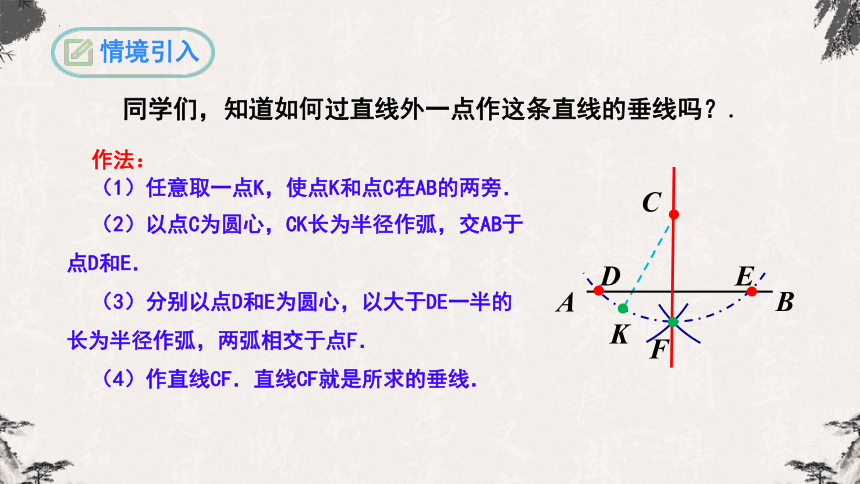
同学们,知道如何过直线外一点作这条直线的垂线吗?.
作法:
(1)任意取一点K,使点K和点C在AB的两旁.
(2)以点C为圆心,CK长为半径作弧,交AB于点D和E.
(3)分别以点D和E为圆心,以大于DE一半的长为半径作弧,两弧相交于点F.
(4)作直线CF.直线CF就是所求的垂线.
K
A
B
C
D
E
F
互动新授
思考:
直观上我们能感觉两个平面图形是成轴对称的,但是如何验证呢?在不折叠图形的情况下,你能准确地做出轴对称图形的对称轴吗?
如果两个图形成轴对称,其对称轴就是任何一对对应点所连线段的垂直平分线.
因此,只要能找到一对对应点,作出连接它们的线段的垂直平分线,就可以得到这两个图形的对称轴.
例2.如图,点A和点B关于某条直线成轴对称,你能试着作出这条直线吗?
分析:我们只要连接点A和点B,作出线段AB的垂直平分线,就可以得到点A和点B的对称轴,为此作出到点A、B距离相等的两点,即线段AB的垂直平分线上的两点,从而作出线段AB的垂直平分线.
A
B
典例精析
例2.如图,点A和点B关于某条直线成轴对称,你能试着作出这条直线吗?
典例精析
作法:如图所示:
(1)分别以点A和点B为圆心,大于 AB的长为半径作弧(想一想为什么),两弧线相交于C,D两点;
(2)作直线CD,即是所求作的直线.
A
B
根据上面例题,你能概括出作对称轴的步骤吗?
互动新授
作对称轴的步骤:
①找:找到轴对称图形或成轴对称的两个图形的任意一对对应点;
②连:连接这对对应点;
③作:做出对应点所连线段的垂直平分线.
注意:找对应点时,一般找图形的顶点或转折点,这样做出的图形更准确.
互动新授
对于如图所示的五角星,可以选择一对对应点A和A′,连接AA′,作出线段AA′的垂直平分线l,则l就是这个五角星的一条对称轴.
A
A′
l
类似的,请你尝试动手作出这个五角星的其他对称轴.
小试牛刀
1.作出下列图形的一条对称轴,和同学比较一下,你们作出的对称轴一样吗?
小试牛刀
2.如图,与图形 A 成轴对称的是哪个图形?画出它的对称轴.
A
B
C
D
课堂检测
1.如图,角是轴对称图形吗?如果是,它的对称轴是什么?
2.如图1-23,在△ABC中,AB = AC,∠A = 120°, AB的垂直平分线交BC于D,求证:CD =2BD.
证明:连结AD
∵D在AB垂直平分线上
∴BD=AD
∴∠B=∠BAD
∵∠BAC=120° AB=AC
∴∠B=∠C=30°
∴∠DAC=90°
在Rt△DAC中 ∵∠C=30° ∴DC=2AD即DC=2BD.
课堂检测
如图,若AC=12,BC=7,AB的垂直平分线交AB于E,交AC于D,求△BCD的周长.
∴BD=AD,
A
B
C
D
E
解:∵ED是线段AB的垂直平分线,
∵ △BCD的周长=BD+DC+BC
∴ △BCD的周长=AD+DC+BC
=AC+BC
=12+7=19.
拓展训练
课堂小结
1、线段垂直平分线的画法.
2、作轴对称图形对称轴的步骤
①找:找到轴对称图形或成轴对称的两个图形的任意一对对应点;
②连:连接这对对应点;
③作:做出对应点所连线段的垂直平分线.
3、运用线段垂直平分线的性质和判定解决实际问题.
1.如图1-21,△ABC中,∠A = 52°, 点O是AC、AB的垂直平分线的交点,则∠OCB = .
2.在△ABC中,AB = AC = 20cm, AB的垂直平分线交AC于点D,若△BCD的周长为32cm,则BC = .
38°
12cm
课后作业
谢谢聆听
第13.1.2线段的垂直平分线的性质
(第二课时)
人教版数学八年级上册
学习目标
1、掌握线段垂直平分线的画法.
2、能正确找出轴对称图形的对称轴.
3、熟练运用线段垂直平分线的性质和判定解决实际问题.
情境引入
同学们,还记得我们上节课学习的线段的垂直平分线的性质和判定吗?.
线段垂直平分线上的点与这条线段两个端点的距离相等.
线段的垂直平分线的性质:
与线段两个端点距离相等的点在这条线段的垂直平分线上.
线段的垂直平分线的判定:
情境引入
同学们,知道如何过直线外一点作这条直线的垂线吗?.
作法:
(1)任意取一点K,使点K和点C在AB的两旁.
(2)以点C为圆心,CK长为半径作弧,交AB于点D和E.
(3)分别以点D和E为圆心,以大于DE一半的长为半径作弧,两弧相交于点F.
(4)作直线CF.直线CF就是所求的垂线.
K
A
B
C
D
E
F
互动新授
思考:
直观上我们能感觉两个平面图形是成轴对称的,但是如何验证呢?在不折叠图形的情况下,你能准确地做出轴对称图形的对称轴吗?
如果两个图形成轴对称,其对称轴就是任何一对对应点所连线段的垂直平分线.
因此,只要能找到一对对应点,作出连接它们的线段的垂直平分线,就可以得到这两个图形的对称轴.
例2.如图,点A和点B关于某条直线成轴对称,你能试着作出这条直线吗?
分析:我们只要连接点A和点B,作出线段AB的垂直平分线,就可以得到点A和点B的对称轴,为此作出到点A、B距离相等的两点,即线段AB的垂直平分线上的两点,从而作出线段AB的垂直平分线.
A
B
典例精析
例2.如图,点A和点B关于某条直线成轴对称,你能试着作出这条直线吗?
典例精析
作法:如图所示:
(1)分别以点A和点B为圆心,大于 AB的长为半径作弧(想一想为什么),两弧线相交于C,D两点;
(2)作直线CD,即是所求作的直线.
A
B
根据上面例题,你能概括出作对称轴的步骤吗?
互动新授
作对称轴的步骤:
①找:找到轴对称图形或成轴对称的两个图形的任意一对对应点;
②连:连接这对对应点;
③作:做出对应点所连线段的垂直平分线.
注意:找对应点时,一般找图形的顶点或转折点,这样做出的图形更准确.
互动新授
对于如图所示的五角星,可以选择一对对应点A和A′,连接AA′,作出线段AA′的垂直平分线l,则l就是这个五角星的一条对称轴.
A
A′
l
类似的,请你尝试动手作出这个五角星的其他对称轴.
小试牛刀
1.作出下列图形的一条对称轴,和同学比较一下,你们作出的对称轴一样吗?
小试牛刀
2.如图,与图形 A 成轴对称的是哪个图形?画出它的对称轴.
A
B
C
D
课堂检测
1.如图,角是轴对称图形吗?如果是,它的对称轴是什么?
2.如图1-23,在△ABC中,AB = AC,∠A = 120°, AB的垂直平分线交BC于D,求证:CD =2BD.
证明:连结AD
∵D在AB垂直平分线上
∴BD=AD
∴∠B=∠BAD
∵∠BAC=120° AB=AC
∴∠B=∠C=30°
∴∠DAC=90°
在Rt△DAC中 ∵∠C=30° ∴DC=2AD即DC=2BD.
课堂检测
如图,若AC=12,BC=7,AB的垂直平分线交AB于E,交AC于D,求△BCD的周长.
∴BD=AD,
A
B
C
D
E
解:∵ED是线段AB的垂直平分线,
∵ △BCD的周长=BD+DC+BC
∴ △BCD的周长=AD+DC+BC
=AC+BC
=12+7=19.
拓展训练
课堂小结
1、线段垂直平分线的画法.
2、作轴对称图形对称轴的步骤
①找:找到轴对称图形或成轴对称的两个图形的任意一对对应点;
②连:连接这对对应点;
③作:做出对应点所连线段的垂直平分线.
3、运用线段垂直平分线的性质和判定解决实际问题.
1.如图1-21,△ABC中,∠A = 52°, 点O是AC、AB的垂直平分线的交点,则∠OCB = .
2.在△ABC中,AB = AC = 20cm, AB的垂直平分线交AC于点D,若△BCD的周长为32cm,则BC = .
38°
12cm
课后作业
谢谢聆听
