13.1.2 线段的垂直平分线的性质 课件 (共21张PPT)
文档属性
| 名称 | 13.1.2 线段的垂直平分线的性质 课件 (共21张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 5.6MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-07-07 06:22:47 | ||
图片预览





文档简介
(共21张PPT)
第13.1.2线段的垂直平分线的性质
(第一课时)
人教版数学八年级上册
学习目标
1、理解并掌握线段垂直平分线的性质和判定的内容.
2、探究线段垂直平分线的性质和判定的过程.
3、熟练运用线段垂直平分线的性质和判定解决实际问题.
情境引入
探究
如图,直线l垂直平分线段AB,P1,P2,P3,……是l上的点,分别量一量点P1,P2,P3,……到点A和点B的距离,你有什么发现?
可以发现,点P1,P2,P3,……到点A的距离与它们到点B的距离分别相等,如果把线段AB沿着直线l对折,线段P1A与P1B,线段P2A与P2B,线段P3A与P3B……都是重合的,因此它们也分别相等.
A
B
l
┐
P1
P2
P3
情境引入
探究
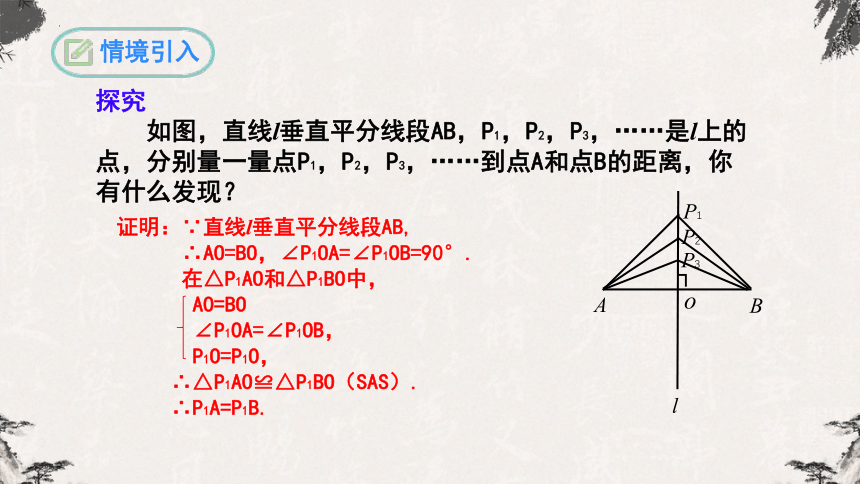
如图,直线l垂直平分线段AB,P1,P2,P3,……是l上的点,分别量一量点P1,P2,P3,……到点A和点B的距离,你有什么发现?
A
B
l
┐
P1
P2
P3
证明:∵直线l垂直平分线段AB,
∴AO=BO,∠P1OA=∠P1OB=90°.
在△P1AO和△P1BO中,
AO=BO
∠P1OA=∠P1OB,
P1O=P1O,
∴△P1AO≌△P1BO(SAS).
∴P1A=P1B.
o
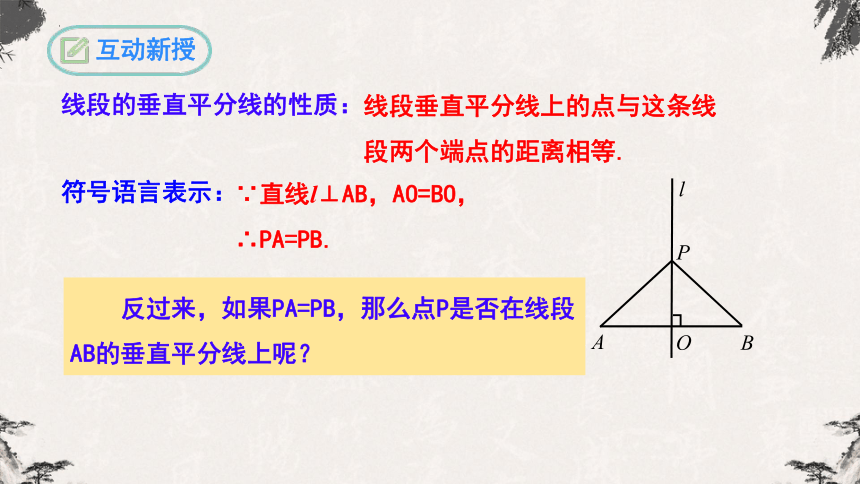
线段垂直平分线上的点与这条线段两个端点的距离相等.
∵直线l⊥AB,AO=BO,
∴PA=PB.
A
B
l
┐
O
P
符号语言表示:
互动新授
线段的垂直平分线的性质:
反过来,如果PA=PB,那么点P是否在线段AB的垂直平分线上呢?
互动新授
A
B
l
┐
O
P
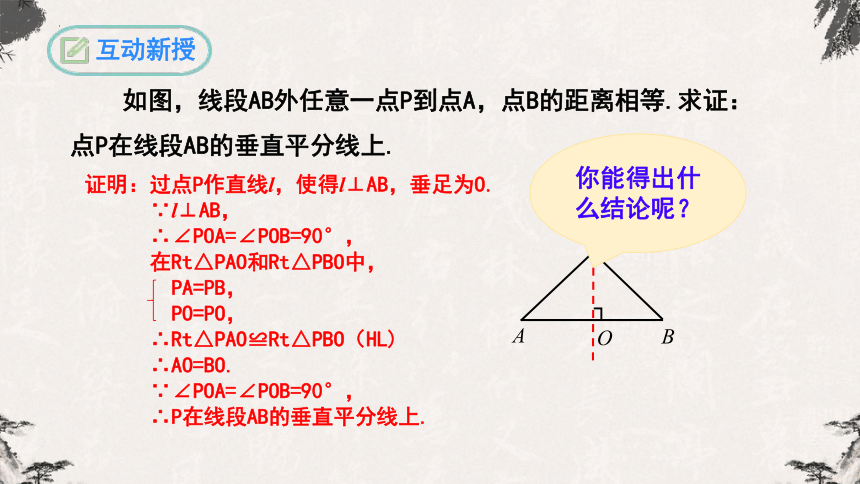
如图,线段AB外任意一点P到点A,点B的距离相等.求证:点P在线段AB的垂直平分线上.
证明:过点P作直线l,使得l⊥AB,垂足为O.
∵l⊥AB,
∴∠POA=∠POB=90°,
在Rt△PAO和Rt△PBO中,
PA=PB,
PO=PO,
∴Rt△PAO≌Rt△PBO(HL)
∴AO=BO.
∵∠POA=∠POB=90°,
∴P在线段AB的垂直平分线上.
你能得出什么结论呢?
互动新授
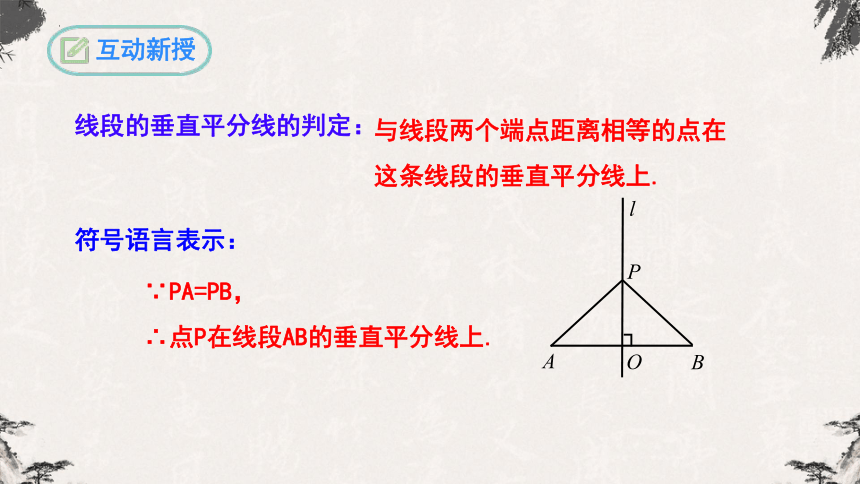
与线段两个端点距离相等的点在这条线段的垂直平分线上.
∵PA=PB,
∴点P在线段AB的垂直平分线上.
符号语言表示:
线段的垂直平分线的判定:
A
B
l
┐
O
P
总结归纳
1、从上面两个结论可以看出,在线段AB的垂直平分线l上的点与点A,B的距离都相等.
2、反过来,与A,B的距离相等的点都在l上,所以直线l可以看成与两点A,B的距离相等的所有点的集合.
A
B
l
┐
O
P
典例精析
例1.尺规作图,经过已知直线外一点作这条直线的垂线.
已知,直线AB和AB外一点C.求作:AB的垂线,使它经过点C.
A
B
B
.
典例精析
作法:
(1)任意取一点K,使点K和点C在AB的两旁.
(2)以点C为圆心,CK长为半径作弧,交AB于点D和E.
K
A
B
C
D
E
典例精析
(3)分别以点D和E为圆心,以大于DE一半的长为半径作弧,两弧相交于点F.
(4)作直线CF.直线CF就是所求的垂线.
K
A
B
C
D
E
F
思考:为什么直线CF就是所求作的垂线?
∵从作法的(2)(3)步可知CD=CE,DF=EF,
∴点C,F都在DE的垂直平分线上.
∴CF就是线段DE的垂直平分线.
∵点D,E在直线AB上,
∴CF就是所求直线AB的垂线.
A
B
C
D
E
F
典例精析
1、要作出线段的垂直平分线,必须找到两个与线段两个端点距离相等的点,才能确定已知线段的垂直平分线.
2、证明一条直线是线段的垂直平分线时,必须证明两个点在线段的垂直平分线上.
总结归纳
小试牛刀
1.已知线段AB和它的外面一点P,
(1)若PA=PB,
则点P在AB的 ;
(2)若点P在AB的 ,
则PA=PB.
垂直平分线上
垂直平分线上
2.下列说法:①若直线PE是线段AB的垂直平分线,则EA=EB,PA=PB;②若PA=PB,EA=EB,则直线PE垂直平分线段AB;③若PA=PB,则点P必是线段AB的垂直平分线上的点;④若EA=EB,则过点E的直线垂直平分线段AB.其中正确的个数有( )
A.1个 B.2个 C.3个 D.4个
3.如图,NM是线段AB的垂直平分线,下列说法正确的有:________.
①AB⊥MN,②AD=DB, ③MN⊥AB,
④MD=DN,⑤AB是MN的垂直平分线.
A
B
M
N
D
C
①②③
小试牛刀
6
第1题图
17cm
2.如图所示,在△ABC中,AC的垂直平分线交AC于E,交BC于D,
△ABD的周长为12cm,AC=5cm,则△ABC的周长是_________
第2题图
C
3.如图,等腰△ABC中,AB=AC,∠A=20°.线段AB的垂直平分线交AB于D,交AC于E,连接BE,则∠CBE等于( )
第3题图
A.20° B.70 ° C.60 ° D.50 °
1.如图,在△ABC中,ED垂直平分BC,CE=5,AE=1,则AB的长为____。
2.如图所示,在△ABC中,AC的垂直平分线交AC于E,交BC于D,
△ABD的周长为12cm,AC=5cm,则△ABC的周长是_________
第2题图
第3题图
A.20° B.70 ° C.60 ° D.50 °
课堂检测
课堂检测
4.如图,若AC=12,BC=7,AB的垂直平分线交AB于E,交AC于D,求△BCD的周长.
∴BD=AD,
A
B
C
D
E
解:∵ED是线段AB的垂直平分线,
∵ △BCD的周长=BD+DC+BC
∴ △BCD的周长=AD+DC+BC
=AC+BC
=12+7=19.
电信部门要S区修建一座电视信号发射塔,如图所示,按照设计要求,发射塔到两个城镇A,B的距离必须相等,到两条高速公路m和n的距离也必须相等,请你确定发射塔应修建在什么位置?在图上标出它的位置.
S
拓展训练
解:如图,应建在m,n夹角(锐角)的角平分线a和线段AB的垂直平分线b的交点P处.
S
a
b
P
课堂小结
线段垂直平分线上的点与这条线段两个端点的距离相等.
1、线段的垂直平分线的性质:
与线段两个端点距离相等的点在这条线段的垂直平分线上.
2、线段的垂直平分线的判定:
课后作业
如图,在△ABC中,AB=5cm,BC的垂直平分线分别交AB,BC于点D,E,△ACD的周长为8cm,求线段AC的长.
解:∵DE为线段BC的垂直平分线,
∴CD=BD.
∴△ACD的周长为AC+AD+CD
=AC+AD+BD
=AC+AB
=8cm.
∵AB=5cm,
∴AC=3cm.
B
C
E
D
A
谢谢聆听
第13.1.2线段的垂直平分线的性质
(第一课时)
人教版数学八年级上册
学习目标
1、理解并掌握线段垂直平分线的性质和判定的内容.
2、探究线段垂直平分线的性质和判定的过程.
3、熟练运用线段垂直平分线的性质和判定解决实际问题.
情境引入
探究
如图,直线l垂直平分线段AB,P1,P2,P3,……是l上的点,分别量一量点P1,P2,P3,……到点A和点B的距离,你有什么发现?
可以发现,点P1,P2,P3,……到点A的距离与它们到点B的距离分别相等,如果把线段AB沿着直线l对折,线段P1A与P1B,线段P2A与P2B,线段P3A与P3B……都是重合的,因此它们也分别相等.
A
B
l
┐
P1
P2
P3
情境引入
探究
如图,直线l垂直平分线段AB,P1,P2,P3,……是l上的点,分别量一量点P1,P2,P3,……到点A和点B的距离,你有什么发现?
A
B
l
┐
P1
P2
P3
证明:∵直线l垂直平分线段AB,
∴AO=BO,∠P1OA=∠P1OB=90°.
在△P1AO和△P1BO中,
AO=BO
∠P1OA=∠P1OB,
P1O=P1O,
∴△P1AO≌△P1BO(SAS).
∴P1A=P1B.
o
线段垂直平分线上的点与这条线段两个端点的距离相等.
∵直线l⊥AB,AO=BO,
∴PA=PB.
A
B
l
┐
O
P
符号语言表示:
互动新授
线段的垂直平分线的性质:
反过来,如果PA=PB,那么点P是否在线段AB的垂直平分线上呢?
互动新授
A
B
l
┐
O
P
如图,线段AB外任意一点P到点A,点B的距离相等.求证:点P在线段AB的垂直平分线上.
证明:过点P作直线l,使得l⊥AB,垂足为O.
∵l⊥AB,
∴∠POA=∠POB=90°,
在Rt△PAO和Rt△PBO中,
PA=PB,
PO=PO,
∴Rt△PAO≌Rt△PBO(HL)
∴AO=BO.
∵∠POA=∠POB=90°,
∴P在线段AB的垂直平分线上.
你能得出什么结论呢?
互动新授
与线段两个端点距离相等的点在这条线段的垂直平分线上.
∵PA=PB,
∴点P在线段AB的垂直平分线上.
符号语言表示:
线段的垂直平分线的判定:
A
B
l
┐
O
P
总结归纳
1、从上面两个结论可以看出,在线段AB的垂直平分线l上的点与点A,B的距离都相等.
2、反过来,与A,B的距离相等的点都在l上,所以直线l可以看成与两点A,B的距离相等的所有点的集合.
A
B
l
┐
O
P
典例精析
例1.尺规作图,经过已知直线外一点作这条直线的垂线.
已知,直线AB和AB外一点C.求作:AB的垂线,使它经过点C.
A
B
B
.
典例精析
作法:
(1)任意取一点K,使点K和点C在AB的两旁.
(2)以点C为圆心,CK长为半径作弧,交AB于点D和E.
K
A
B
C
D
E
典例精析
(3)分别以点D和E为圆心,以大于DE一半的长为半径作弧,两弧相交于点F.
(4)作直线CF.直线CF就是所求的垂线.
K
A
B
C
D
E
F
思考:为什么直线CF就是所求作的垂线?
∵从作法的(2)(3)步可知CD=CE,DF=EF,
∴点C,F都在DE的垂直平分线上.
∴CF就是线段DE的垂直平分线.
∵点D,E在直线AB上,
∴CF就是所求直线AB的垂线.
A
B
C
D
E
F
典例精析
1、要作出线段的垂直平分线,必须找到两个与线段两个端点距离相等的点,才能确定已知线段的垂直平分线.
2、证明一条直线是线段的垂直平分线时,必须证明两个点在线段的垂直平分线上.
总结归纳
小试牛刀
1.已知线段AB和它的外面一点P,
(1)若PA=PB,
则点P在AB的 ;
(2)若点P在AB的 ,
则PA=PB.
垂直平分线上
垂直平分线上
2.下列说法:①若直线PE是线段AB的垂直平分线,则EA=EB,PA=PB;②若PA=PB,EA=EB,则直线PE垂直平分线段AB;③若PA=PB,则点P必是线段AB的垂直平分线上的点;④若EA=EB,则过点E的直线垂直平分线段AB.其中正确的个数有( )
A.1个 B.2个 C.3个 D.4个
3.如图,NM是线段AB的垂直平分线,下列说法正确的有:________.
①AB⊥MN,②AD=DB, ③MN⊥AB,
④MD=DN,⑤AB是MN的垂直平分线.
A
B
M
N
D
C
①②③
小试牛刀
6
第1题图
17cm
2.如图所示,在△ABC中,AC的垂直平分线交AC于E,交BC于D,
△ABD的周长为12cm,AC=5cm,则△ABC的周长是_________
第2题图
C
3.如图,等腰△ABC中,AB=AC,∠A=20°.线段AB的垂直平分线交AB于D,交AC于E,连接BE,则∠CBE等于( )
第3题图
A.20° B.70 ° C.60 ° D.50 °
1.如图,在△ABC中,ED垂直平分BC,CE=5,AE=1,则AB的长为____。
2.如图所示,在△ABC中,AC的垂直平分线交AC于E,交BC于D,
△ABD的周长为12cm,AC=5cm,则△ABC的周长是_________
第2题图
第3题图
A.20° B.70 ° C.60 ° D.50 °
课堂检测
课堂检测
4.如图,若AC=12,BC=7,AB的垂直平分线交AB于E,交AC于D,求△BCD的周长.
∴BD=AD,
A
B
C
D
E
解:∵ED是线段AB的垂直平分线,
∵ △BCD的周长=BD+DC+BC
∴ △BCD的周长=AD+DC+BC
=AC+BC
=12+7=19.
电信部门要S区修建一座电视信号发射塔,如图所示,按照设计要求,发射塔到两个城镇A,B的距离必须相等,到两条高速公路m和n的距离也必须相等,请你确定发射塔应修建在什么位置?在图上标出它的位置.
S
拓展训练
解:如图,应建在m,n夹角(锐角)的角平分线a和线段AB的垂直平分线b的交点P处.
S
a
b
P
课堂小结
线段垂直平分线上的点与这条线段两个端点的距离相等.
1、线段的垂直平分线的性质:
与线段两个端点距离相等的点在这条线段的垂直平分线上.
2、线段的垂直平分线的判定:
课后作业
如图,在△ABC中,AB=5cm,BC的垂直平分线分别交AB,BC于点D,E,△ACD的周长为8cm,求线段AC的长.
解:∵DE为线段BC的垂直平分线,
∴CD=BD.
∴△ACD的周长为AC+AD+CD
=AC+AD+BD
=AC+AB
=8cm.
∵AB=5cm,
∴AC=3cm.
B
C
E
D
A
谢谢聆听
