北师大版九年级下册 3.4 圆周角和圆心角的关系(第2课时 ) 课件((共17张PPT))
文档属性
| 名称 | 北师大版九年级下册 3.4 圆周角和圆心角的关系(第2课时 ) 课件((共17张PPT)) |

|
|
| 格式 | pptx | ||
| 文件大小 | 586.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-07-07 00:00:00 | ||
图片预览


文档简介
(共17张PPT)
第3章 圆
3.4 圆周角和圆心角的关系
第2课时 圆周角定理的推论
创设情境,引入新课
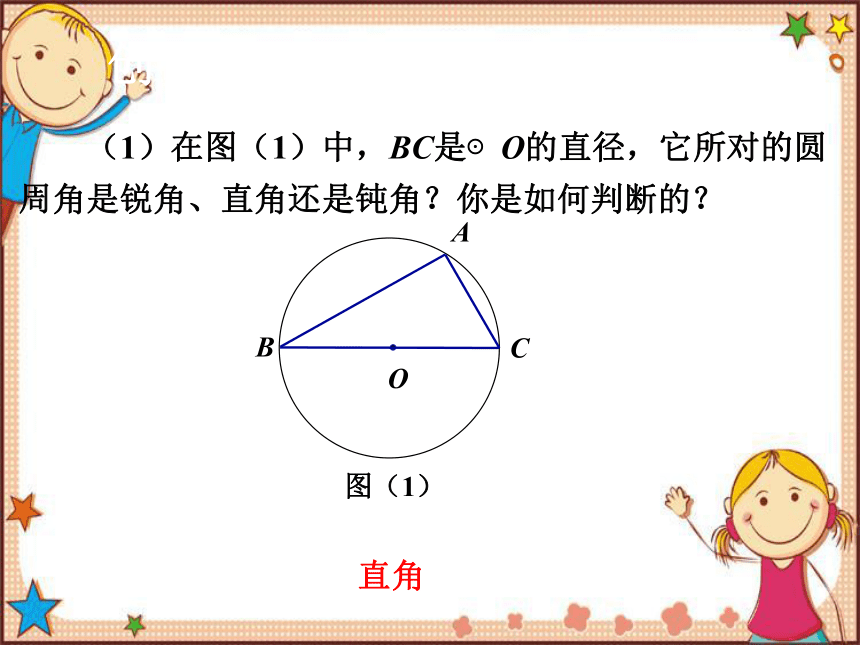
(1)在图(1)中,BC是⊙O的直径,它所对的圆周角是锐角、直角还是钝角?你是如何判断的?
直角
O
B
C
A
图(1)
创设情境,引入新课
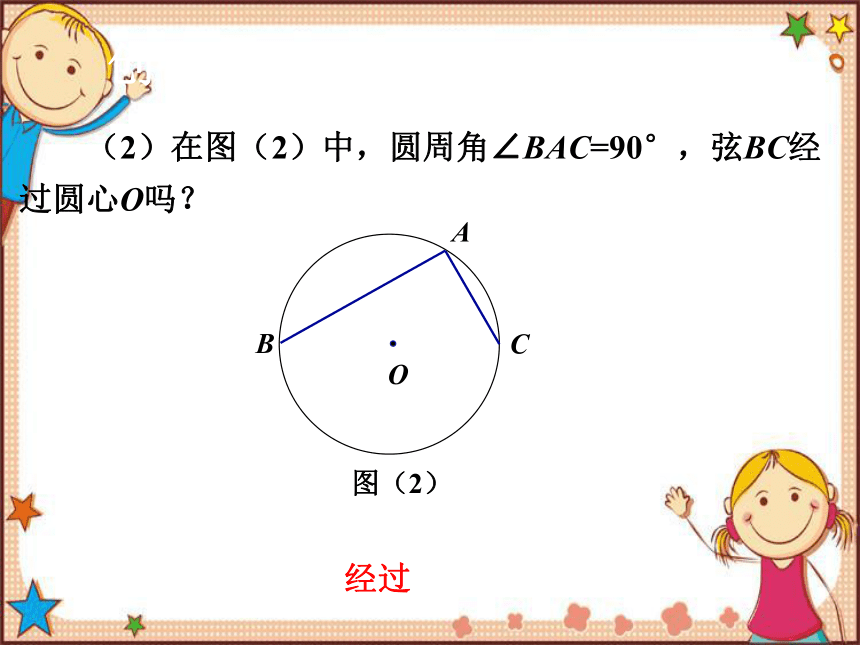
(2)在图(2)中,圆周角∠BAC=90°,弦BC经过圆心O吗?
经过
O
B
C
A
图(2)
创设情境,引入新课
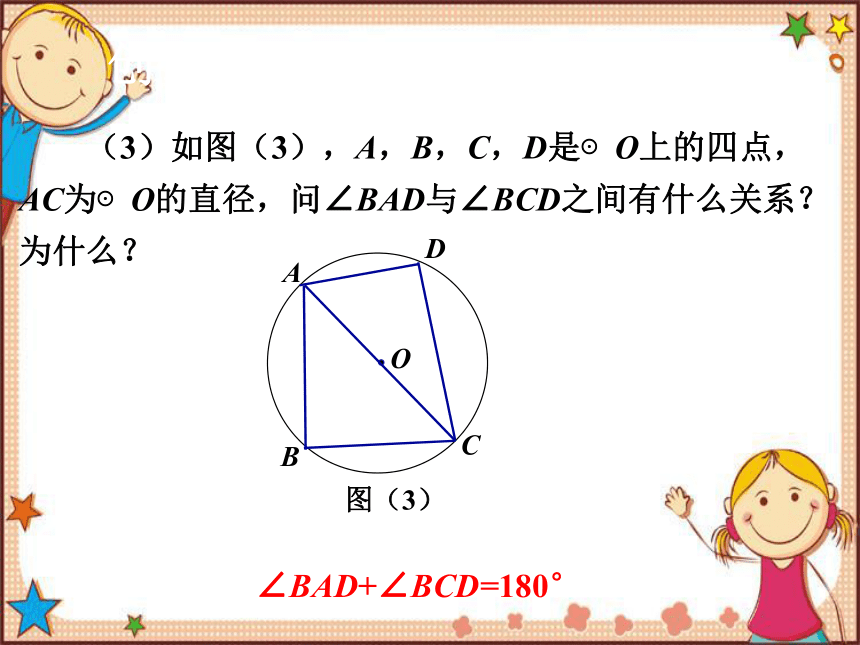
(3)如图(3),A,B,C,D是⊙O上的四点,AC为⊙O的直径,问∠BAD与∠BCD之间有什么关系?为什么?
∠BAD+∠BCD=180°
O
B
C
D
图(3)
A
创设情境,引入新课
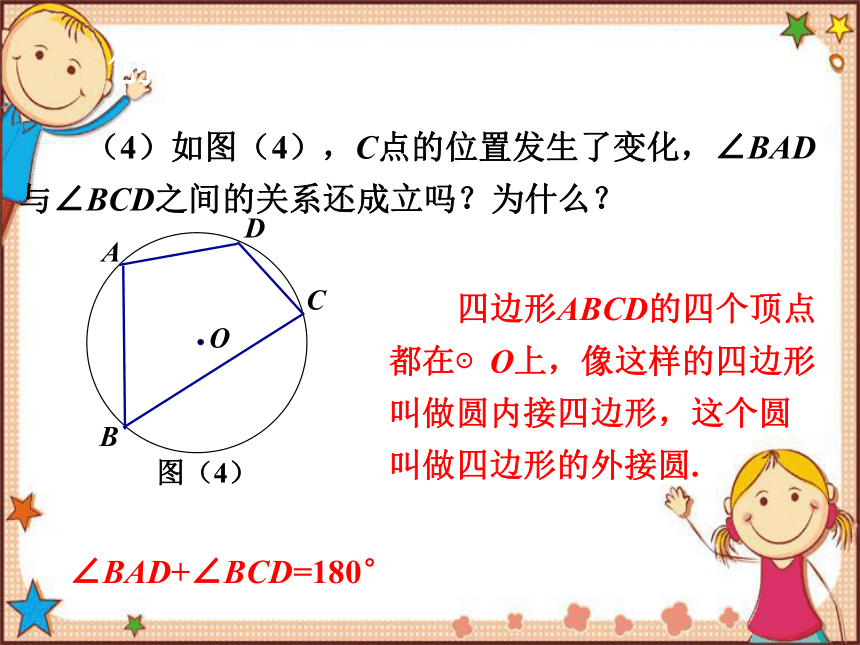
(4)如图(4),C点的位置发生了变化,∠BAD与∠BCD之间的关系还成立吗?为什么?
图(4)
四边形ABCD的四个顶点都在⊙O上,像这样的四边形叫做圆内接四边形,这个圆叫做四边形的外接圆.
O
B
C
D
A
∠BAD+∠BCD=180°
由以上的讨论我们可以得到:
圆内接四边形的性质1:
圆内接四边形的对角互补.
创设情境,引入新课
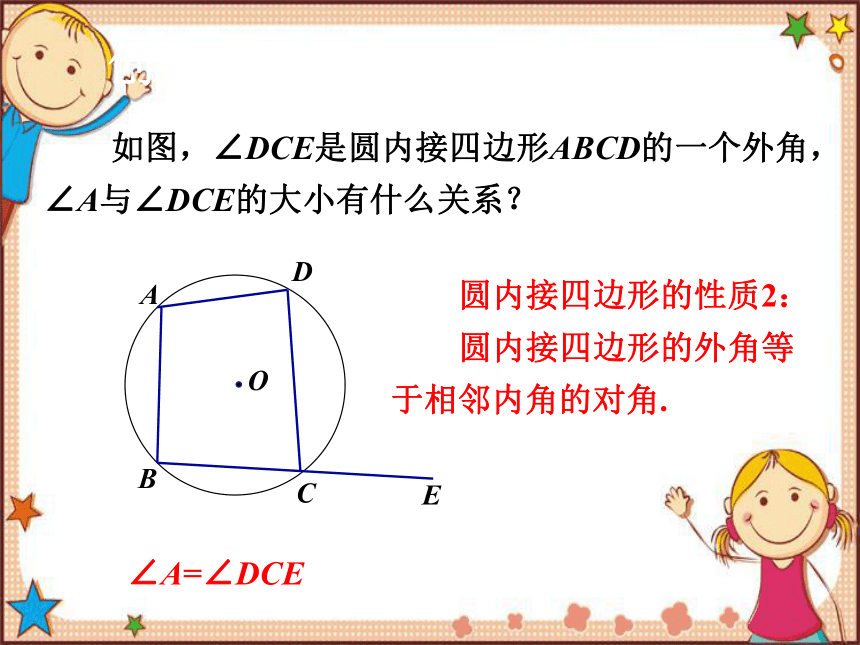
如图,∠DCE是圆内接四边形ABCD的一个外角,∠A与∠DCE的大小有什么关系?
O
B
C
D
A
E
∠A=∠DCE
圆内接四边形的性质2:
圆内接四边形的外角等于相邻内角的对角.
创设情境,引入新课
归纳小结:
(1)圆周角定理推论2:直径所对的圆周角是直角;90°的圆周角所对的弦是直径.
(2)圆内接四边形的性质1:圆内接四边形的对角互补.
(3)圆内接四边形的性质2:圆内接四边形的外角等于相邻内角的对角.
创设情境,引入新课
如图,∠ADB=90°;∠AED+∠B=180°,
∠BAE+∠BDE=180°;∠CED=∠B,∠CDE=∠BAE.
O
C
B
D
A
E
创设情境,引入新课
例 如图,点A,B,C,D在⊙O上,O在∠D的内部,四边形OABC为平行四边形,求∠OAD+∠OCD的度数.
O
B
C
D
A
解:∵∠AOC和∠D分别是弧ABC
所对的圆心角和圆周角,
∴∠AOC=2∠D.
∵四边形OABC是平行四边形, ∴∠B=∠AOC.
又∵圆内接四边形对角互补,即∠B+∠D=180°,
∴∠D=60°.
如图,连接OD,则OA=OD,OD=OC.
∴∠OAD=∠ODA , ∠OCD=∠ODC ,
∴∠OAD+∠OCD=∠ODA+∠ODC=60°.
创设情境,引入新课
随堂练习,巩固应用
如图,⊙O的直径AB=10 cm,C为⊙O上一点,∠B=30°,求AC的长.
O
B
A
C
AC=5 cm
随堂练习,巩固应用
小明想用直角尺检查某些工件是否恰好为半圆形.下面所示的四种弧形,你能判断哪个是半圆形吗?为什么?
(2)为半圆形
原因: 90°的圆周角所对的弦是直径.
随堂练习,巩固应用
在圆内接四边形ABCD中,对角∠A与∠C的度数之比是4 ∶ 5,求∠C的度数.
∠C=100°
随堂练习,巩固应用
如图,在⊙O中,∠BOD=80°,求∠A和∠C的度数.
∠A= 40°,∠C= 140°
O
B
A
C
D
1.直径所对的圆周角是直角;90°的圆周角所对的弦是直径.
2.圆内接四边形的对角互补.
3.圆内接四边形的外角等于相邻内角的对角.
课堂小结
教材第84页习题3.5第2,3题.
布置作业
谢谢大家!
再见!
第3章 圆
3.4 圆周角和圆心角的关系
第2课时 圆周角定理的推论
创设情境,引入新课
(1)在图(1)中,BC是⊙O的直径,它所对的圆周角是锐角、直角还是钝角?你是如何判断的?
直角
O
B
C
A
图(1)
创设情境,引入新课
(2)在图(2)中,圆周角∠BAC=90°,弦BC经过圆心O吗?
经过
O
B
C
A
图(2)
创设情境,引入新课
(3)如图(3),A,B,C,D是⊙O上的四点,AC为⊙O的直径,问∠BAD与∠BCD之间有什么关系?为什么?
∠BAD+∠BCD=180°
O
B
C
D
图(3)
A
创设情境,引入新课
(4)如图(4),C点的位置发生了变化,∠BAD与∠BCD之间的关系还成立吗?为什么?
图(4)
四边形ABCD的四个顶点都在⊙O上,像这样的四边形叫做圆内接四边形,这个圆叫做四边形的外接圆.
O
B
C
D
A
∠BAD+∠BCD=180°
由以上的讨论我们可以得到:
圆内接四边形的性质1:
圆内接四边形的对角互补.
创设情境,引入新课
如图,∠DCE是圆内接四边形ABCD的一个外角,∠A与∠DCE的大小有什么关系?
O
B
C
D
A
E
∠A=∠DCE
圆内接四边形的性质2:
圆内接四边形的外角等于相邻内角的对角.
创设情境,引入新课
归纳小结:
(1)圆周角定理推论2:直径所对的圆周角是直角;90°的圆周角所对的弦是直径.
(2)圆内接四边形的性质1:圆内接四边形的对角互补.
(3)圆内接四边形的性质2:圆内接四边形的外角等于相邻内角的对角.
创设情境,引入新课
如图,∠ADB=90°;∠AED+∠B=180°,
∠BAE+∠BDE=180°;∠CED=∠B,∠CDE=∠BAE.
O
C
B
D
A
E
创设情境,引入新课
例 如图,点A,B,C,D在⊙O上,O在∠D的内部,四边形OABC为平行四边形,求∠OAD+∠OCD的度数.
O
B
C
D
A
解:∵∠AOC和∠D分别是弧ABC
所对的圆心角和圆周角,
∴∠AOC=2∠D.
∵四边形OABC是平行四边形, ∴∠B=∠AOC.
又∵圆内接四边形对角互补,即∠B+∠D=180°,
∴∠D=60°.
如图,连接OD,则OA=OD,OD=OC.
∴∠OAD=∠ODA , ∠OCD=∠ODC ,
∴∠OAD+∠OCD=∠ODA+∠ODC=60°.
创设情境,引入新课
随堂练习,巩固应用
如图,⊙O的直径AB=10 cm,C为⊙O上一点,∠B=30°,求AC的长.
O
B
A
C
AC=5 cm
随堂练习,巩固应用
小明想用直角尺检查某些工件是否恰好为半圆形.下面所示的四种弧形,你能判断哪个是半圆形吗?为什么?
(2)为半圆形
原因: 90°的圆周角所对的弦是直径.
随堂练习,巩固应用
在圆内接四边形ABCD中,对角∠A与∠C的度数之比是4 ∶ 5,求∠C的度数.
∠C=100°
随堂练习,巩固应用
如图,在⊙O中,∠BOD=80°,求∠A和∠C的度数.
∠A= 40°,∠C= 140°
O
B
A
C
D
1.直径所对的圆周角是直角;90°的圆周角所对的弦是直径.
2.圆内接四边形的对角互补.
3.圆内接四边形的外角等于相邻内角的对角.
课堂小结
教材第84页习题3.5第2,3题.
布置作业
谢谢大家!
再见!
