北师大版数学九年级下册 3.8 圆内接正多边形 课件(共19张PPT)
文档属性
| 名称 | 北师大版数学九年级下册 3.8 圆内接正多边形 课件(共19张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 430.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-07-07 18:13:44 | ||
图片预览



文档简介
(共19张PPT)
第3章 圆
3.8 圆内接正多边形
情境引入
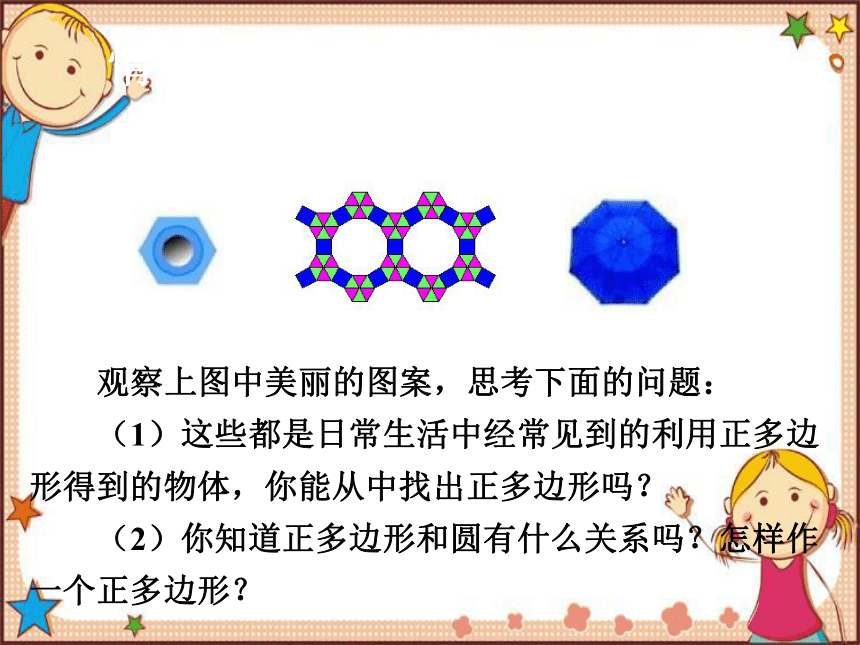
观察上图中美丽的图案,思考下面的问题:
(1)这些都是日常生活中经常见到的利用正多边形得到的物体,你能从中找出正多边形吗?
(2)你知道正多边形和圆有什么关系吗?怎样作一个正多边形?
O
自主探究
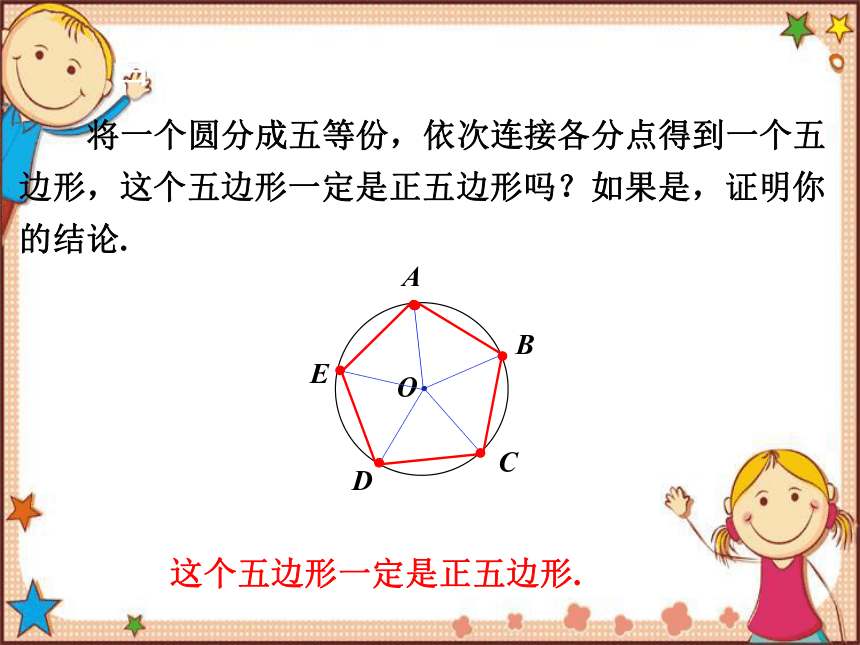
将一个圆分成五等份,依次连接各分点得到一个五边形,这个五边形一定是正五边形吗?如果是,证明你的结论.
这个五边形一定是正五边形.
A
B
C
D
E
自主探究
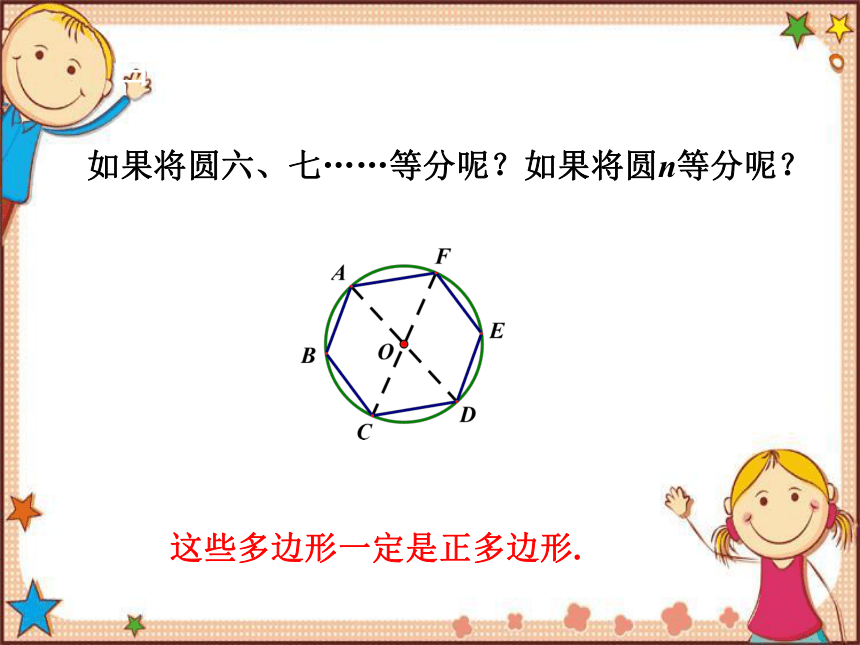
如果将圆六、七……等分呢?如果将圆n等分呢?
这些多边形一定是正多边形.
自主探究
小结:将一个圆分成n等份(n≥3),依次连接各分点得到一个正n边形,这个n边形叫做圆内接正n边形.
自主探究
以圆内接正六边形为例证明,如图所示的圆,我们把⊙O分成相等的六段弧,依次连接各分点得到六边形ABCDEF,下面证明它是正六边形.
自主探究
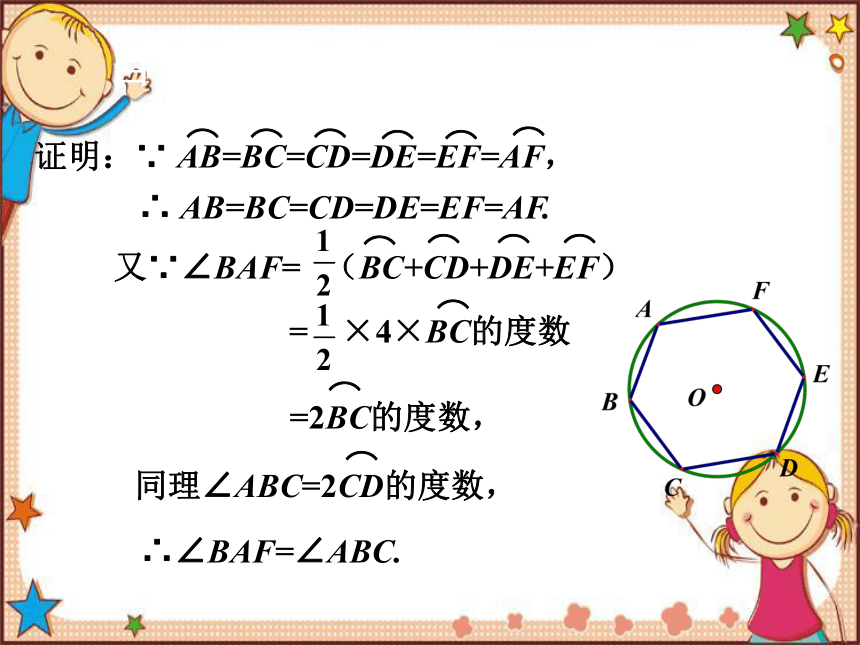
证明:∵ AB=BC=CD=DE=EF=AF,
︵
︵
︵
︵
︵
︵
∴ AB=BC=CD=DE=EF=AF.
又∵∠BAF= (BC+CD+DE+EF)
= ×4×BC的度数
同理∠ABC=2CD的度数,
︵
︵
︵
︵
=2BC的度数,
︵
︵
︵
∴∠BAF=∠ABC.
自主探究
又∵六边形ABCDEF的顶点都在⊙O上,
∴ 六边形ABCDEF是⊙O内接正六边形, ⊙O是正六边形ABCDEF的外接圆.
同理可证:∠ABC=∠BCD=∠CDE=∠DEF=∠AFE=∠BAF.
自主探究
正多边形的有关概念:
正多边形外接圆的圆心叫做正多边形的中心;
正多边形外接圆的半径叫做正多边形的半径;
正多边形每一边所对的圆心角叫做正多边形的中心角;
中心到正多边形的一边的
距离叫做正多边形的边心距.
自主探究
中心、半径、中心角、边心距之间的关系:
a
R
r
O
A
B
C
自主探究
正多边形的性质:
① 正多边形的一个内角等于 ;
② 中心角: ;
③正多边形中心角的度数等于外角的度数.
自主探究
例1. 在圆内接正六边形ABCDEF中,半径OC=4, OG⊥BC,垂足为G,求这个正六边形的中心角、边长和边心距.
解:连接OD.
∵六边形ABCDEF为正六边形,
∴△COD为等边三角形.
∴CD=OC=4.
在Rt△COG中,OC=4,
∴正六边形ABCDEF的中心角为60°,边长为4,边心距为
G
自主探究
生活中经常遇到正多边形,怎么画正多边形呢?
以正六边形为例:
方法一:首先画一个圆,然后对圆六等分,顺次连接各点得正六边形;
方法二:正六边形的边长和圆的半径相等,可以在圆上顺次截取等于半径的弦.
正三角形、正十二边形怎么画?
自主探究
例2.一位同学在作圆的内接正五边形时,先做了如下几个步骤:
①作⊙O的两条相互垂直的直径,再作OA的垂直平分线交OA于点M,如图;
②以M为圆心,BM长为半径作圆弧,交CA于点D,连接BD,如图.若⊙O的半径为1,则由以上作图得到的关于正五边形边长BD的等式是 ( )
O
A
C
B
M
D
C
自主探究
解:如图,连接BM,根据题意得:
OB=OA=1,AD⊥OB,BM=DM.
∵OA的垂直平分线交OA于点M,
O
A
C
B
M
D
巩固练习
随堂练习
分别求出半径为6 cm的圆内接正三角形的边长和边心距.
O
P
A
B
C
学完这节课,你有哪些收获?
在解决有关正多边形和圆的计算问题时,通常是正多边形的边、表示边心距的线段、半径构成直角三角形,运用垂径定理和勾股定理解决.
总结提高
作业:
教材第99页习题3.10第1,2,3题.
总结提高
谢谢大家!
再见!
第3章 圆
3.8 圆内接正多边形
情境引入
观察上图中美丽的图案,思考下面的问题:
(1)这些都是日常生活中经常见到的利用正多边形得到的物体,你能从中找出正多边形吗?
(2)你知道正多边形和圆有什么关系吗?怎样作一个正多边形?
O
自主探究
将一个圆分成五等份,依次连接各分点得到一个五边形,这个五边形一定是正五边形吗?如果是,证明你的结论.
这个五边形一定是正五边形.
A
B
C
D
E
自主探究
如果将圆六、七……等分呢?如果将圆n等分呢?
这些多边形一定是正多边形.
自主探究
小结:将一个圆分成n等份(n≥3),依次连接各分点得到一个正n边形,这个n边形叫做圆内接正n边形.
自主探究
以圆内接正六边形为例证明,如图所示的圆,我们把⊙O分成相等的六段弧,依次连接各分点得到六边形ABCDEF,下面证明它是正六边形.
自主探究
证明:∵ AB=BC=CD=DE=EF=AF,
︵
︵
︵
︵
︵
︵
∴ AB=BC=CD=DE=EF=AF.
又∵∠BAF= (BC+CD+DE+EF)
= ×4×BC的度数
同理∠ABC=2CD的度数,
︵
︵
︵
︵
=2BC的度数,
︵
︵
︵
∴∠BAF=∠ABC.
自主探究
又∵六边形ABCDEF的顶点都在⊙O上,
∴ 六边形ABCDEF是⊙O内接正六边形, ⊙O是正六边形ABCDEF的外接圆.
同理可证:∠ABC=∠BCD=∠CDE=∠DEF=∠AFE=∠BAF.
自主探究
正多边形的有关概念:
正多边形外接圆的圆心叫做正多边形的中心;
正多边形外接圆的半径叫做正多边形的半径;
正多边形每一边所对的圆心角叫做正多边形的中心角;
中心到正多边形的一边的
距离叫做正多边形的边心距.
自主探究
中心、半径、中心角、边心距之间的关系:
a
R
r
O
A
B
C
自主探究
正多边形的性质:
① 正多边形的一个内角等于 ;
② 中心角: ;
③正多边形中心角的度数等于外角的度数.
自主探究
例1. 在圆内接正六边形ABCDEF中,半径OC=4, OG⊥BC,垂足为G,求这个正六边形的中心角、边长和边心距.
解:连接OD.
∵六边形ABCDEF为正六边形,
∴△COD为等边三角形.
∴CD=OC=4.
在Rt△COG中,OC=4,
∴正六边形ABCDEF的中心角为60°,边长为4,边心距为
G
自主探究
生活中经常遇到正多边形,怎么画正多边形呢?
以正六边形为例:
方法一:首先画一个圆,然后对圆六等分,顺次连接各点得正六边形;
方法二:正六边形的边长和圆的半径相等,可以在圆上顺次截取等于半径的弦.
正三角形、正十二边形怎么画?
自主探究
例2.一位同学在作圆的内接正五边形时,先做了如下几个步骤:
①作⊙O的两条相互垂直的直径,再作OA的垂直平分线交OA于点M,如图;
②以M为圆心,BM长为半径作圆弧,交CA于点D,连接BD,如图.若⊙O的半径为1,则由以上作图得到的关于正五边形边长BD的等式是 ( )
O
A
C
B
M
D
C
自主探究
解:如图,连接BM,根据题意得:
OB=OA=1,AD⊥OB,BM=DM.
∵OA的垂直平分线交OA于点M,
O
A
C
B
M
D
巩固练习
随堂练习
分别求出半径为6 cm的圆内接正三角形的边长和边心距.
O
P
A
B
C
学完这节课,你有哪些收获?
在解决有关正多边形和圆的计算问题时,通常是正多边形的边、表示边心距的线段、半径构成直角三角形,运用垂径定理和勾股定理解决.
总结提高
作业:
教材第99页习题3.10第1,2,3题.
总结提高
谢谢大家!
再见!
