北师大版数学八年级下册 6.4 多边形的内角和与外角和 课件(共25张PPT)
文档属性
| 名称 | 北师大版数学八年级下册 6.4 多边形的内角和与外角和 课件(共25张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 193.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-07-07 18:14:31 | ||
图片预览






文档简介
(共25张PPT)
第6章 平行四边形
6.4 多边形的内角和与外角和
引入新课
三角形内角和定理的内容是什么?
定理:三角形的内角和为180°.
还记得我们是怎么验证这一结论的吗?
方法一:通过具体的测量,可知三角形的内角和为180°.
引入新课
三角形内角和定理的内容是什么?
定理:三角形的内角和为180°.
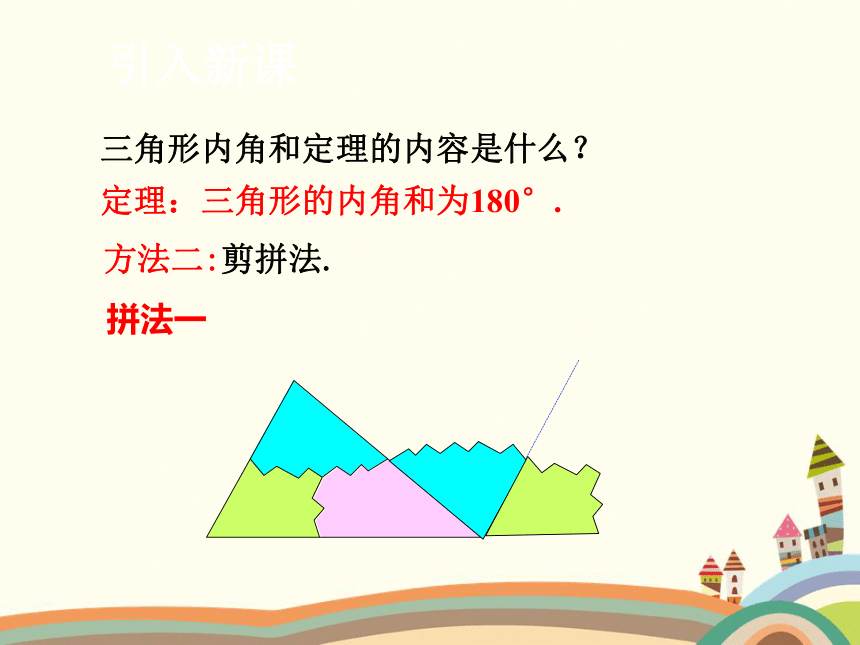
方法二:剪拼法.
拼法一
引入新课
三角形内角和定理的内容是什么?
定理:三角形的内角和为180°.
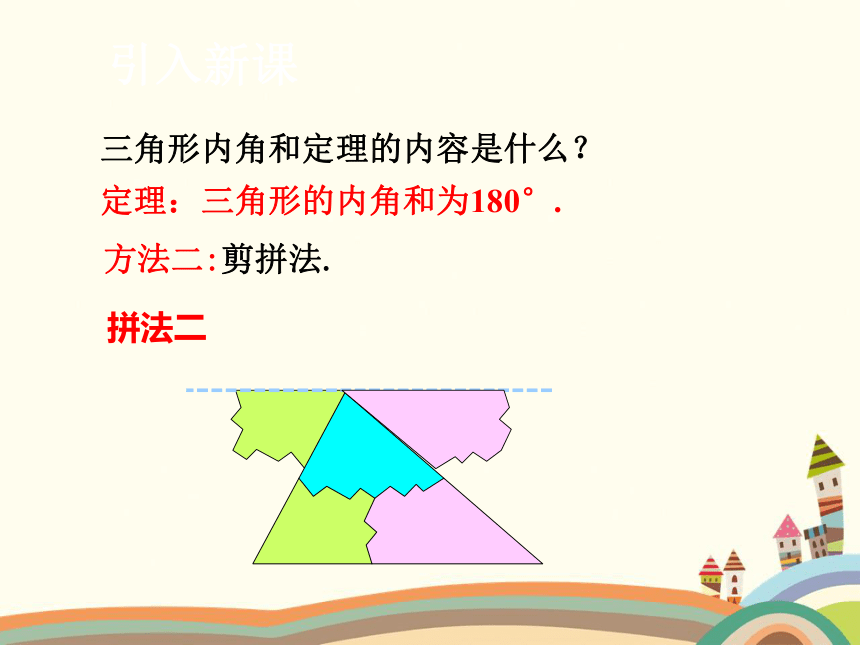
方法二:剪拼法.
拼法二
引入新课
四边形内角和等于多少?
动手验证一下吧!
任意画一个四边形,通过测量这个四边形各个内角的度数,可计算出四边形内角和约为360°.
引入新课
五边形内角和等于多少?
动手验证一下吧!
任意画一个五边形,通过测量这个五边形各个内角的度数,可计算出五边形内角和约为540°.
引导学生观察、猜想n(n≥3)边形内角和
n=3时,三边形内角和为180°=1× 180°.
n=4时,四边形内角和为360°=2× 180°.
n=5时,五边形内角和为540°=3× 180°.
想一想:六边形、七边形、十边形、n边形的内角和分别是多少?
小组讨论,找一找规律吧!
引导学生观察、猜想n(n≥3)边形内角和
n=3时,三边形内角和为180°=1× 180°.
n=4时,四边形内角和为360°=2× 180°.
n=5时,五边形内角和为540°=3× 180°.
想一想:六边形、七边形、十边形、n边形的内角和分别是多少?
猜想:
n (n≥3)边形内角和等于(n-2)·180°.
引导学生证明
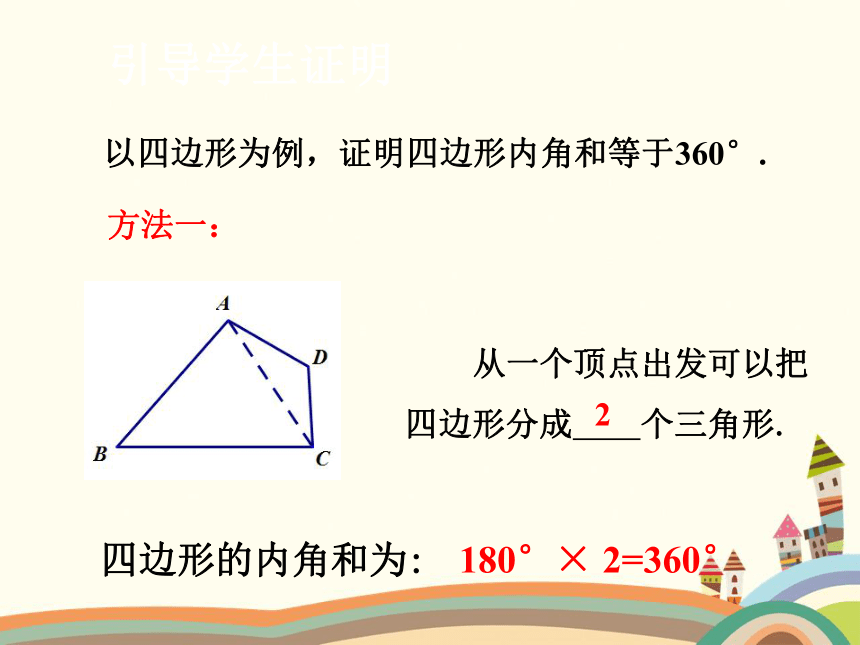
以四边形为例,证明四边形内角和等于360°.
方法一:
从一个顶点出发可以把四边形分成 个三角形.
2
四边形的内角和为:
180°× 2=360°
引导学生证明
以四边形为例,证明四边形内角和等于360°.
方法二:
四边形的内角和为:
从一边上任意一点可以把四边形分成 个三角形.
3
180°×3-180°=360°
引导学生证明
以四边形为例,证明四边形内角和等于360°.
方法三:
四边形的内角和为:
从四边形内一点出发可以把四边形分成 个三角形.
4
180°×4-360°=360°
引导学生证明
以四边形为例,证明四边形内角和等于360°.
方法四:
四边形的内角和为:
从四边形外任意一点出发可以把四边形分成 个三角形.
3
180° × 3-180°=360°
引导学生证明
方法一:
从一个顶点出发可以把n边形分成 个三角形.
n -2
n边形的内角和为:
(n-2)·180°
类比四边形内角和的证明过程,证明n边形内角和等于(n -2)·180°.
引导学生证明
方法二:
n边形的内角和为:
(n -1)·180°-180°=(n -2)·180°
类比四边形内角和的证明过程,证明n边形内角和等于(n -2)·180°.
从一边上任意一点可以把n边形分成 个三角形.
n-1
从n边形内一点出发可以把n边形分成 个三角形.
引导学生证明
方法三:
n边形的内角和为:
n ·180°-360°=(n-2)·180°
类比四边形内角和的证明过程,证明n边形内角和等于(n-2)·180°.
n
从n边形外任意一点出发可以把n边形分成 个三角形.
引导学生证明
方法四:
n边形的内角和为:
类比四边形内角和的证明过程,证明n边形内角和等于(n-2)·180°.
n-1
(n -1)·180°-180°=(n -2)·180°
引导学生证明
类比四边形内角和的证明过程,证明n边形内角和等于(n-2)·180°.
多边形的内角和仅与边数有关,与多边形的大小、形状无关.
给出多边形外角的定义,并画图说明
多边形的外角是如何定义的?
思考:n(n≥3)边形外角和等于多少?
多边形的边与它的邻边的延长线组成的角叫做多边形的外角.
n边形外角和为
n·180°- (n-2)·180°=360°.
给出多边形外角的定义,并画图说明
n(n≥3)边形外角和等于多少?
任意多边形的外角和等于360°.
说明:多边形外角和为一定值,与边数无关.
想一想:内角和与外角和相等的多边形是几边形?
解:由 (n-2)·180°=360°,得n =4.
故内角和与外角和相等的多边形是四边形.
练习
1.六角螺母的一个面是六边形,它的六个内角相等,则一个内角的度数为多少?
解:设它的一个内角的度数为x°,
则 (6-2) ×180°=6 x ,得x =120.
故它的一个内角的度数为120°.
2.一个多边形的每一个外角都等于72°,这个多边形是_____边形,它的每一个内角是_____度.
五
108
练习
3.四边形的四个内角可以都是锐角吗?可以都是钝角吗?可以都是直角吗?为什么?
解:四边形的四个内角不可以都是锐角,若都是锐角,即都小于90°,那么四个内角的和就小于360°;
四边形的四个内角不可以都是钝角,若都是钝角,即都大于90°,那么四个内角的和就大于360°;
四边形的四个内角可以都是直角,若都是直角,即都等于90°,那么四个内角的和就恰好等于360°,满足四边形的内角和定理.
练习
4.已知一个多边形,它的内角和等于外角和的2倍,求这个多边形的边数.
解:设这个多边形的边数为n,
则 (n-2)·180°=360°×2,得n =6.
故这个多边形的边数为6.
1. n边形内角和等于(n-2)·180°.
2.任意多边形的外角和都等于360°.
3.本节课用到了类比、转化、从特殊到一般及归纳等方法,利用了方程思想解决多边形内角和、外角和的有关计算.
总结
布置作业
必做题:教材习题6.7和习题6.8.
选做题:1.在多边形的内角中,锐角的个数不能多于( )个.
A.2 B.3 C.4 D.5
2.一个凸多边形除了一个内角外,其余各内角之和为2 570°,则这个角等于多少度?
谢谢大家!
再见!
第6章 平行四边形
6.4 多边形的内角和与外角和
引入新课
三角形内角和定理的内容是什么?
定理:三角形的内角和为180°.
还记得我们是怎么验证这一结论的吗?
方法一:通过具体的测量,可知三角形的内角和为180°.
引入新课
三角形内角和定理的内容是什么?
定理:三角形的内角和为180°.
方法二:剪拼法.
拼法一
引入新课
三角形内角和定理的内容是什么?
定理:三角形的内角和为180°.
方法二:剪拼法.
拼法二
引入新课
四边形内角和等于多少?
动手验证一下吧!
任意画一个四边形,通过测量这个四边形各个内角的度数,可计算出四边形内角和约为360°.
引入新课
五边形内角和等于多少?
动手验证一下吧!
任意画一个五边形,通过测量这个五边形各个内角的度数,可计算出五边形内角和约为540°.
引导学生观察、猜想n(n≥3)边形内角和
n=3时,三边形内角和为180°=1× 180°.
n=4时,四边形内角和为360°=2× 180°.
n=5时,五边形内角和为540°=3× 180°.
想一想:六边形、七边形、十边形、n边形的内角和分别是多少?
小组讨论,找一找规律吧!
引导学生观察、猜想n(n≥3)边形内角和
n=3时,三边形内角和为180°=1× 180°.
n=4时,四边形内角和为360°=2× 180°.
n=5时,五边形内角和为540°=3× 180°.
想一想:六边形、七边形、十边形、n边形的内角和分别是多少?
猜想:
n (n≥3)边形内角和等于(n-2)·180°.
引导学生证明
以四边形为例,证明四边形内角和等于360°.
方法一:
从一个顶点出发可以把四边形分成 个三角形.
2
四边形的内角和为:
180°× 2=360°
引导学生证明
以四边形为例,证明四边形内角和等于360°.
方法二:
四边形的内角和为:
从一边上任意一点可以把四边形分成 个三角形.
3
180°×3-180°=360°
引导学生证明
以四边形为例,证明四边形内角和等于360°.
方法三:
四边形的内角和为:
从四边形内一点出发可以把四边形分成 个三角形.
4
180°×4-360°=360°
引导学生证明
以四边形为例,证明四边形内角和等于360°.
方法四:
四边形的内角和为:
从四边形外任意一点出发可以把四边形分成 个三角形.
3
180° × 3-180°=360°
引导学生证明
方法一:
从一个顶点出发可以把n边形分成 个三角形.
n -2
n边形的内角和为:
(n-2)·180°
类比四边形内角和的证明过程,证明n边形内角和等于(n -2)·180°.
引导学生证明
方法二:
n边形的内角和为:
(n -1)·180°-180°=(n -2)·180°
类比四边形内角和的证明过程,证明n边形内角和等于(n -2)·180°.
从一边上任意一点可以把n边形分成 个三角形.
n-1
从n边形内一点出发可以把n边形分成 个三角形.
引导学生证明
方法三:
n边形的内角和为:
n ·180°-360°=(n-2)·180°
类比四边形内角和的证明过程,证明n边形内角和等于(n-2)·180°.
n
从n边形外任意一点出发可以把n边形分成 个三角形.
引导学生证明
方法四:
n边形的内角和为:
类比四边形内角和的证明过程,证明n边形内角和等于(n-2)·180°.
n-1
(n -1)·180°-180°=(n -2)·180°
引导学生证明
类比四边形内角和的证明过程,证明n边形内角和等于(n-2)·180°.
多边形的内角和仅与边数有关,与多边形的大小、形状无关.
给出多边形外角的定义,并画图说明
多边形的外角是如何定义的?
思考:n(n≥3)边形外角和等于多少?
多边形的边与它的邻边的延长线组成的角叫做多边形的外角.
n边形外角和为
n·180°- (n-2)·180°=360°.
给出多边形外角的定义,并画图说明
n(n≥3)边形外角和等于多少?
任意多边形的外角和等于360°.
说明:多边形外角和为一定值,与边数无关.
想一想:内角和与外角和相等的多边形是几边形?
解:由 (n-2)·180°=360°,得n =4.
故内角和与外角和相等的多边形是四边形.
练习
1.六角螺母的一个面是六边形,它的六个内角相等,则一个内角的度数为多少?
解:设它的一个内角的度数为x°,
则 (6-2) ×180°=6 x ,得x =120.
故它的一个内角的度数为120°.
2.一个多边形的每一个外角都等于72°,这个多边形是_____边形,它的每一个内角是_____度.
五
108
练习
3.四边形的四个内角可以都是锐角吗?可以都是钝角吗?可以都是直角吗?为什么?
解:四边形的四个内角不可以都是锐角,若都是锐角,即都小于90°,那么四个内角的和就小于360°;
四边形的四个内角不可以都是钝角,若都是钝角,即都大于90°,那么四个内角的和就大于360°;
四边形的四个内角可以都是直角,若都是直角,即都等于90°,那么四个内角的和就恰好等于360°,满足四边形的内角和定理.
练习
4.已知一个多边形,它的内角和等于外角和的2倍,求这个多边形的边数.
解:设这个多边形的边数为n,
则 (n-2)·180°=360°×2,得n =6.
故这个多边形的边数为6.
1. n边形内角和等于(n-2)·180°.
2.任意多边形的外角和都等于360°.
3.本节课用到了类比、转化、从特殊到一般及归纳等方法,利用了方程思想解决多边形内角和、外角和的有关计算.
总结
布置作业
必做题:教材习题6.7和习题6.8.
选做题:1.在多边形的内角中,锐角的个数不能多于( )个.
A.2 B.3 C.4 D.5
2.一个凸多边形除了一个内角外,其余各内角之和为2 570°,则这个角等于多少度?
谢谢大家!
再见!
同课章节目录
- 第一章 三角形的证明
- 1 等腰三角形
- 2 直角三角形
- 3 线段的垂直平分线
- 4 角平分线
- 第二章 一元一次不等式和一元一次不等式组
- 1 不等关系
- 2 不等式的基本性质
- 3 不等式的解集
- 4 一元一次不等式
- 5 一元一次不等式与一次函数
- 6 一元一次不等式组
- 第三章 图形的平移与旋转
- 1 图形的平移
- 2 图形的旋转
- 3 中心对称
- 4 简单的图案设计
- 第四章 因式分解
- 1 因式分解
- 2 提公因式法
- 3 公式法
- 第五章 分式与分式方程
- 1 认识分式
- 2 分式的乘除法
- 3 分式的加减法
- 4 分式方程
- 第六章 平行四边形
- 1 平行四边形的性质
- 2 平行四边形的判定
- 3 三角形的中位线
- 4 多边形的内角与外角和
