§2.2 匀变速直线运动的速度与时间的关系教学设计
文档属性
| 名称 | §2.2 匀变速直线运动的速度与时间的关系教学设计 |  | |
| 格式 | zip | ||
| 文件大小 | 113.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 物理 | ||
| 更新时间 | 2013-06-24 21:51:41 | ||
图片预览

文档简介
课题:§2.2 匀变速直线运动的速度与时间的关系教学设计
授课人:刘立军
课型:新授课
授课班级:高一(05)(08)(12)班
授课时间:2013年10月14日
三维目标
知识与技能:
掌握匀变速直线运动的概念,知道匀变速直线运动的v-t图象的特点,会根据图象分析解决问题;
掌握匀变速匀速直线运动的速度与时间关系的描述式,能进行有关的运算。
过程与方法:
通过探究匀变速直线运动速度的表达式,经历由特殊到一般的过程,体会科学的研究方法;
通过类比寻找规律得出匀变速直线运动的概念,并用数学语言描述物理规律,给出各符号的具体含义。
情感态度与价值观:
通过数学描述式的导出过程,培养用科学的语言表达物理规律的意识,激发学生探索与创新的欲望;
通过v-t图象的理解及应用,培养学生透过现象看本质,用不同方法(语言)描述同一规律的科学意识。
教学重点
匀变速直线运动的定义;
匀变速直线运动的速度的数学描述式和导出。
教学难点
匀变速直线运动相关图象的理解;
灵活运用匀变速直线运动速度的数学表达式解决实际问题。
课时安排:一课时
教学准备:作图工具 小黑板
教学方法:讨论法 讲授法
教学过程
新课引入:
同学们,我一不小心就很荣幸地发现了一个天大的秘密,什么秘密呢?我发现所有的语言都是对某一特定客观事实的描述,语言可以不同,事实在只有一个。比如说:茶杯,数学的语言研究描述半径R,高H,体积了什么的;画家哗、哗、两笔画出来了;音乐的语言呢,谈一谈,唱一唱,跳一跳就描述出来了。这就是所谓的高科技,就是科学,你可以迷恋它,但不可以迷信它,它也许真的只是一个传说。
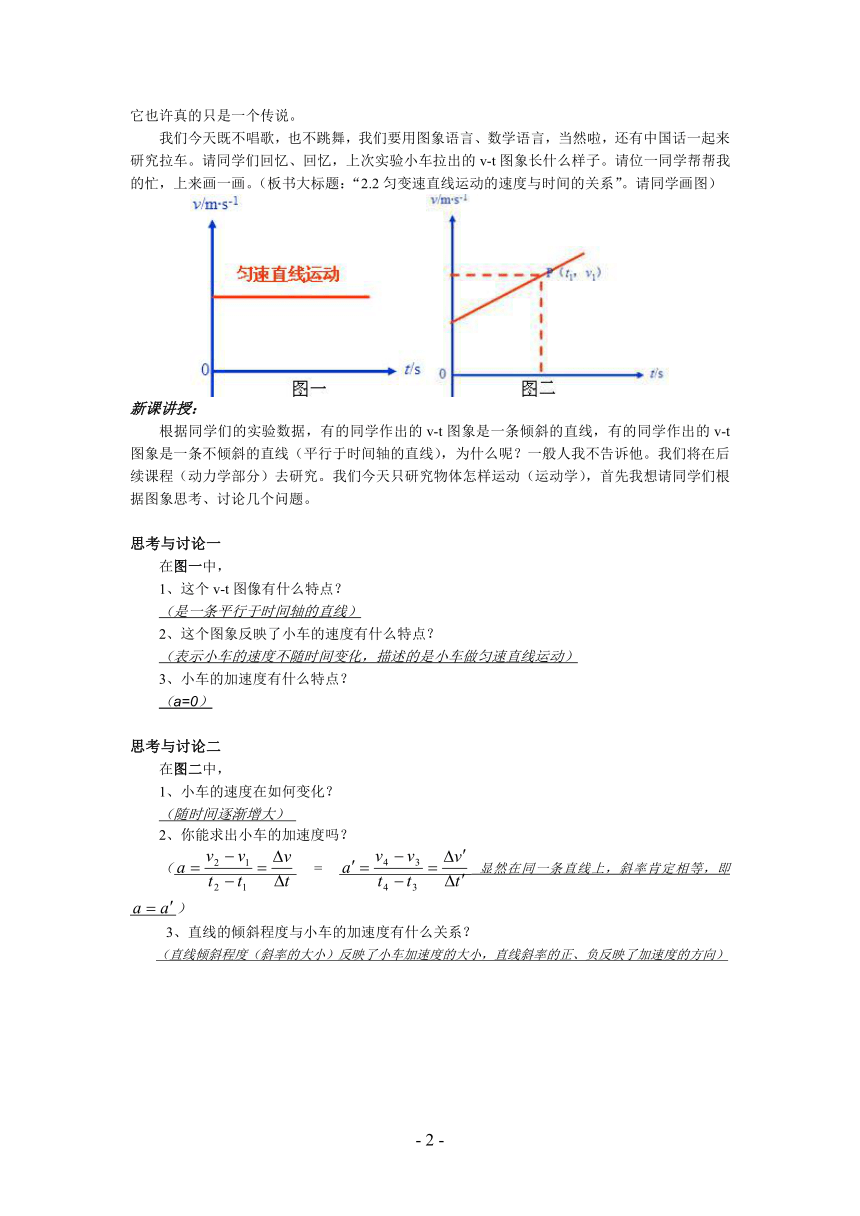
我们今天既不唱歌,也不跳舞,我们要用图象语言、数学语言,当然啦,还有中国话一起来研究拉车。请同学们回忆、回忆,上次实验小车拉出的v-t图象长什么样子。请位一同学帮帮我的忙,上来画一画。(板书大标题:“2.2匀变速直线运动的速度与时间的关系”。请同学画图)
新课讲授:
根据同学们的实验数据,有的同学作出的v-t图象是一条倾斜的直线,有的同学作出的v-t图象是一条不倾斜的直线(平行于时间轴的直线),为什么呢?一般人我不告诉他。我们将在后续课程(动力学部分)去研究。我们今天只研究物体怎样运动(运动学),首先我想请同学们根据图象思考、讨论几个问题。
思考与讨论一
在图一中,
1、这个v-t图像有什么特点?
(是一条平行于时间轴的直线)
2、这个图象反映了小车的速度有什么特点?
(表示小车的速度不随时间变化,描述的是小车做匀速直线运动)
3、小车的加速度有什么特点?
(a=0)
思考与讨论二
在图二中,
1、小车的速度在如何变化?
(随时间逐渐增大)
2、你能求出小车的加速度吗?
( = 显然在同一条直线上,斜率肯定相等,即)
3、直线的倾斜程度与小车的加速度有什么关系?
(直线倾斜程度(斜率的大小)反映了小车加速度的大小,直线斜率的正、负反映了加速度的方向)
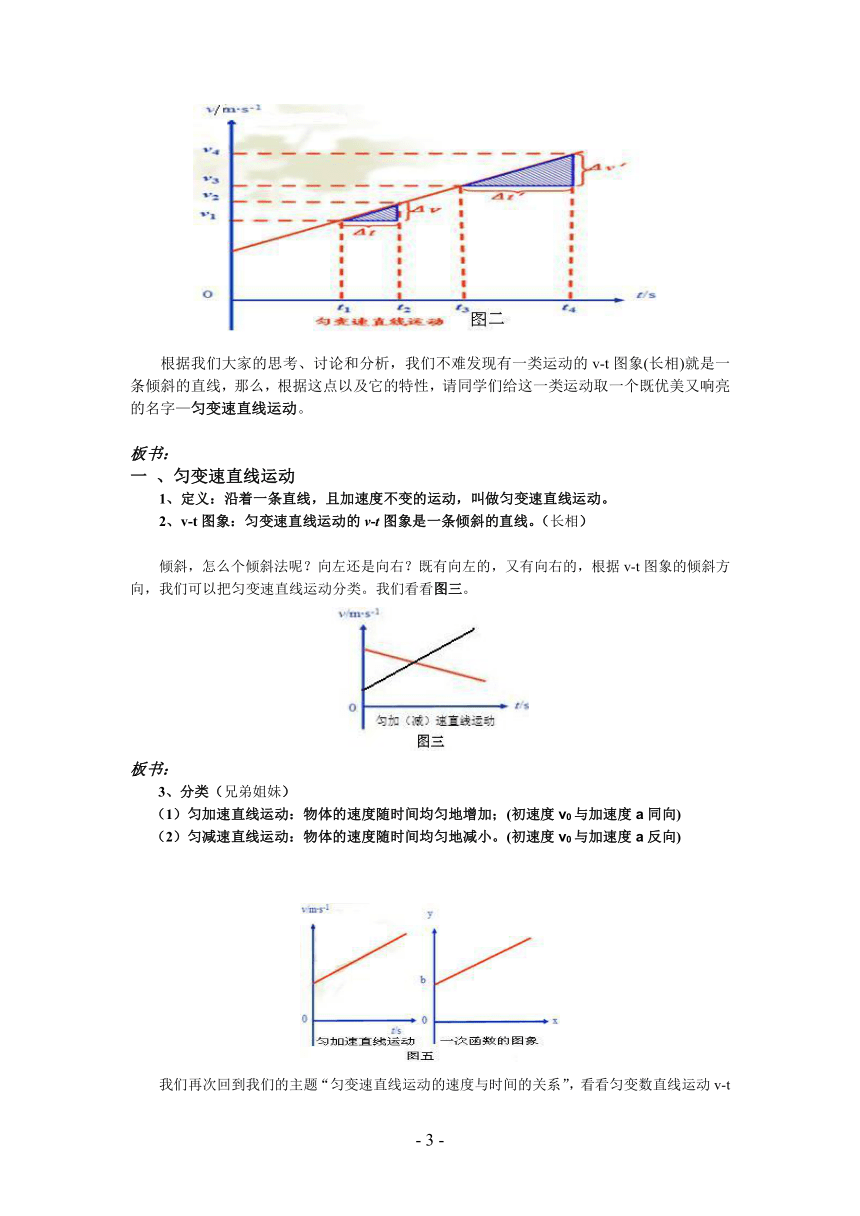
根据我们大家的思考、讨论和分析,我们不难发现有一类运动的v-t图象(长相)就是一条倾斜的直线,那么,根据这点以及它的特性,请同学们给这一类运动取一个既优美又响亮的名字—匀变速直线运动。
板书:
一 、匀变速直线运动
1、定义:沿着一条直线,且加速度不变的运动,叫做匀变速直线运动。
2、v-t图象:匀变速直线运动的v-t图象是一条倾斜的直线。(长相)
倾斜,怎么个倾斜法呢?向左还是向右?既有向左的,又有向右的,根据v-t图象的倾斜方向,我们可以把匀变速直线运动分类。我们看看图三。
板书:
3、分类(兄弟姐妹)
(1)匀加速直线运动:物体的速度随时间均匀地增加;(初速度v0与加速度a同向)
(2)匀减速直线运动:物体的速度随时间均匀地减小。(初速度v0与加速度a反向)
我们再次回到我们的主题“匀变速直线运动的速度与时间的关系”,看看匀变数直线运动v-t图象的样子,请同学们思考下面的问题。
思考与讨论三
1、匀变速直线运动的v-t图象与我们在数学里学的什么图象类似?它们之间有联系吗?
(匀变速直线运动的v-t图象与我们在数学里学一次函数的图象类似,有一定的联系,我们赋予了一次函数的坐标轴特定的物理含义)
2、你能不能将图中所示的一次函数的一般表达式写出来?
(,k值与图象有什么关系?b表示什么?k描写了直线的倾斜程度(斜率),b表示截距)
3、你能否类比一次函数的表达式,猜想一下图五中左图所示的速度与时间的关系式吗?
( 的话,同学们,看清楚了,见证历史的时刻到了,党和国家的命运就交给你们了,则)
板书:
二、速度与时间的关系式
1、表达式:(遥控器)
结合一次函数的图象和表达式,我们可以猜出描述匀变速直线运动的速度与时间的关系式为:,它表达了什么呢?我们一起来回顾一下第一章第五节加速度的定义,,如果我们规定物体运动开始时刻为计时起点(即0时刻),它有此时的速度为:(),物体走啊走,走到哪儿呢?走到丁字口,什么时刻呢?到了时刻,速度变为多少呢? 时刻速度为(也可用表示),那么,时间变化量为:;速度的变化量为:。可有:
这样我们也可以得到,这就是匀变速直线运动的速度与时间的关系式。
2、理解
这个表达式有什么意义、反映了什么呢?请同学们阅读教材P35的第一段,“可以这样理解:由于加速度在数值上等于单位时间内速度的变化量,所以就是整个运动过程中速度的变化量;再加上运动开始时物体的速度,就得到时刻物体的速度。”
换句话说:式中,表示物体做匀变速直线运动的初速度,表示加速度,表示运动过程对应的时间,描述物体的末速度,描写物体速度的变化量。用图象语言可描写为图六。
我们对作一个小小的讨论。
3、讨论(时间不够可以省略):
(1)当时,,物体做初速度为的匀变速直线运动。(两种情况:>,<)
(2)当时,物体做匀速直线运动。
(3)当,时,物体静止。
4、注意(时间不够可选择强调)
(1)适用于匀变速直线运动。
(2)运用此关系式处理问题需先明确研究过程。
(3)V、V0、都是矢量,方向不一定相同, 在直线运动中,如果选定了该直线的一个方向为正方向,则凡与规定正方向相同的矢量在公式中取正值,凡与规定正方向相反的矢量在公式中取负值。因此,应先规定正方向。(一般以V0的方向为正方向,则对于匀加速直线运动,加速度取正值;对于匀减速直线运动,加速度取负值。)
(4)统一国际单位制。
好啦!同学们,搞清楚了上面这些之后,我们一起来实践实践,解决一些实际问题。
板书:
三、 速度表达式的简单应用
例1:汽车以40km/h的速度匀速行驶,现以0.6m/s2的加速度加速,10s后的速度能达到多少?
解:选取初速度方向为x轴正方向建立直线坐标系。
初速度v0=40km/h=11m/s,加速度a=0.6m/s2,时间t=10s,10s后的速度为v,则:
v=v0+at
=11m/s+0.6m/s2×10s
=17m/s=61km/h
例题2:某汽车在紧急刹车时加速度的大小是6m/s2,如果必须在2s内停下来,汽车的行驶速度最高不能超过多少?
解:选取初速度方向为正方向建立直线坐标系。
加速度a= -6m/s2,时间t=2s,2s末的速度v=0,根据v=v0+at我们有初速度,则:
v0=v-at
=0-(-0.6m/s2)×2s
=12m/s
=43km/h
同学们,我们今天都在和图象交流、对话,接下来,请同学们看到P35的“说一说”,思考和讨论以下问题:
思考与讨论四(如果时间紧迫可以略讲,引导学生看教材)
1、如图图四是一个物体运动的v-t图象,它的速度怎样变化?
(随时间逐渐增加)
2、在相等的时间间隔内(),速度的变化量(与)总是相等吗?
(不相等, 不变,越来越小,也越来越小)
3、物体在做匀变速直线运动吗?
(物体做加速度逐渐减小的加速直线运动)
显然,这个图象长得不像我们所说的匀变速直线运动的样子,它描述的是物体做加速度逐渐减小的加速直线运动,不是我们刚才所说的匀变速直线运动。所以,从图象研究运动情况是:长相决定命运;如果从运动情况来探究图象则为:命运决定长相。
有的同学也许会问:它怎么就是“物体做加速度逐渐减小的加速直线运动“呢?图象上明明就是弯的嘛!应该是做加速度逐渐减小的曲线运动才对。同学们,请注意!看看它的坐标是什么?速度和时间,它描述的速度v与时间t的关系,不是物体运动的轨迹。所以这就提醒我们,看问题不要光看外表,要透过现象去探究本质。(看人也一样)。
课堂小结
1、匀变速直线运动
沿着一条直线,且加速度不变的运动叫做匀变速直线运动。匀变速直线运动的v-t图象是一条倾斜的直线。
2、匀变速直线运动的速度与时间的关系
图像描述:匀变速直线运动的v-t图象是一条倾斜的直线。速度随时间均匀变化。
公式表述:v=v0+at
3、在运用速度公式解题时要注意公式的矢量性
布置作业
1、课本P36《问题与练习》T2、T4(作业本上交);
2、三维设计对应的内容;
3、报纸对应的内容。
今天的故事就讲到这里,欲知后事如何,且听下回分解,下课,同学们再见!
板书设计
一 、匀变速直线运动
1、定义:沿着一条直线,且加速度不变的运动,叫做匀变速直线运动。
2、v-t图象:匀变速直线运动的v-t图象是一条倾斜的直线。
3、分类
(1)匀加速直线运动:物体的速度随时间均匀地增加;(初速度v0与加速度a同向)
(2)匀减速直线运动:物体的速度随时间均匀地减小。(初速度v0与加速度a反向)
二、速度与时间的关系式
1、表达式:
2、理解
3、讨论(时间不够可以省略):
4、注意(强调)
三、 速度表达式的简单应用
课后反思与修改
授课人:刘立军
课型:新授课
授课班级:高一(05)(08)(12)班
授课时间:2013年10月14日
三维目标
知识与技能:
掌握匀变速直线运动的概念,知道匀变速直线运动的v-t图象的特点,会根据图象分析解决问题;
掌握匀变速匀速直线运动的速度与时间关系的描述式,能进行有关的运算。
过程与方法:
通过探究匀变速直线运动速度的表达式,经历由特殊到一般的过程,体会科学的研究方法;
通过类比寻找规律得出匀变速直线运动的概念,并用数学语言描述物理规律,给出各符号的具体含义。
情感态度与价值观:
通过数学描述式的导出过程,培养用科学的语言表达物理规律的意识,激发学生探索与创新的欲望;
通过v-t图象的理解及应用,培养学生透过现象看本质,用不同方法(语言)描述同一规律的科学意识。
教学重点
匀变速直线运动的定义;
匀变速直线运动的速度的数学描述式和导出。
教学难点
匀变速直线运动相关图象的理解;
灵活运用匀变速直线运动速度的数学表达式解决实际问题。
课时安排:一课时
教学准备:作图工具 小黑板
教学方法:讨论法 讲授法
教学过程
新课引入:
同学们,我一不小心就很荣幸地发现了一个天大的秘密,什么秘密呢?我发现所有的语言都是对某一特定客观事实的描述,语言可以不同,事实在只有一个。比如说:茶杯,数学的语言研究描述半径R,高H,体积了什么的;画家哗、哗、两笔画出来了;音乐的语言呢,谈一谈,唱一唱,跳一跳就描述出来了。这就是所谓的高科技,就是科学,你可以迷恋它,但不可以迷信它,它也许真的只是一个传说。
我们今天既不唱歌,也不跳舞,我们要用图象语言、数学语言,当然啦,还有中国话一起来研究拉车。请同学们回忆、回忆,上次实验小车拉出的v-t图象长什么样子。请位一同学帮帮我的忙,上来画一画。(板书大标题:“2.2匀变速直线运动的速度与时间的关系”。请同学画图)
新课讲授:
根据同学们的实验数据,有的同学作出的v-t图象是一条倾斜的直线,有的同学作出的v-t图象是一条不倾斜的直线(平行于时间轴的直线),为什么呢?一般人我不告诉他。我们将在后续课程(动力学部分)去研究。我们今天只研究物体怎样运动(运动学),首先我想请同学们根据图象思考、讨论几个问题。
思考与讨论一
在图一中,
1、这个v-t图像有什么特点?
(是一条平行于时间轴的直线)
2、这个图象反映了小车的速度有什么特点?
(表示小车的速度不随时间变化,描述的是小车做匀速直线运动)
3、小车的加速度有什么特点?
(a=0)
思考与讨论二
在图二中,
1、小车的速度在如何变化?
(随时间逐渐增大)
2、你能求出小车的加速度吗?
( = 显然在同一条直线上,斜率肯定相等,即)
3、直线的倾斜程度与小车的加速度有什么关系?
(直线倾斜程度(斜率的大小)反映了小车加速度的大小,直线斜率的正、负反映了加速度的方向)
根据我们大家的思考、讨论和分析,我们不难发现有一类运动的v-t图象(长相)就是一条倾斜的直线,那么,根据这点以及它的特性,请同学们给这一类运动取一个既优美又响亮的名字—匀变速直线运动。
板书:
一 、匀变速直线运动
1、定义:沿着一条直线,且加速度不变的运动,叫做匀变速直线运动。
2、v-t图象:匀变速直线运动的v-t图象是一条倾斜的直线。(长相)
倾斜,怎么个倾斜法呢?向左还是向右?既有向左的,又有向右的,根据v-t图象的倾斜方向,我们可以把匀变速直线运动分类。我们看看图三。
板书:
3、分类(兄弟姐妹)
(1)匀加速直线运动:物体的速度随时间均匀地增加;(初速度v0与加速度a同向)
(2)匀减速直线运动:物体的速度随时间均匀地减小。(初速度v0与加速度a反向)
我们再次回到我们的主题“匀变速直线运动的速度与时间的关系”,看看匀变数直线运动v-t图象的样子,请同学们思考下面的问题。
思考与讨论三
1、匀变速直线运动的v-t图象与我们在数学里学的什么图象类似?它们之间有联系吗?
(匀变速直线运动的v-t图象与我们在数学里学一次函数的图象类似,有一定的联系,我们赋予了一次函数的坐标轴特定的物理含义)
2、你能不能将图中所示的一次函数的一般表达式写出来?
(,k值与图象有什么关系?b表示什么?k描写了直线的倾斜程度(斜率),b表示截距)
3、你能否类比一次函数的表达式,猜想一下图五中左图所示的速度与时间的关系式吗?
( 的话,同学们,看清楚了,见证历史的时刻到了,党和国家的命运就交给你们了,则)
板书:
二、速度与时间的关系式
1、表达式:(遥控器)
结合一次函数的图象和表达式,我们可以猜出描述匀变速直线运动的速度与时间的关系式为:,它表达了什么呢?我们一起来回顾一下第一章第五节加速度的定义,,如果我们规定物体运动开始时刻为计时起点(即0时刻),它有此时的速度为:(),物体走啊走,走到哪儿呢?走到丁字口,什么时刻呢?到了时刻,速度变为多少呢? 时刻速度为(也可用表示),那么,时间变化量为:;速度的变化量为:。可有:
这样我们也可以得到,这就是匀变速直线运动的速度与时间的关系式。
2、理解
这个表达式有什么意义、反映了什么呢?请同学们阅读教材P35的第一段,“可以这样理解:由于加速度在数值上等于单位时间内速度的变化量,所以就是整个运动过程中速度的变化量;再加上运动开始时物体的速度,就得到时刻物体的速度。”
换句话说:式中,表示物体做匀变速直线运动的初速度,表示加速度,表示运动过程对应的时间,描述物体的末速度,描写物体速度的变化量。用图象语言可描写为图六。
我们对作一个小小的讨论。
3、讨论(时间不够可以省略):
(1)当时,,物体做初速度为的匀变速直线运动。(两种情况:>,<)
(2)当时,物体做匀速直线运动。
(3)当,时,物体静止。
4、注意(时间不够可选择强调)
(1)适用于匀变速直线运动。
(2)运用此关系式处理问题需先明确研究过程。
(3)V、V0、都是矢量,方向不一定相同, 在直线运动中,如果选定了该直线的一个方向为正方向,则凡与规定正方向相同的矢量在公式中取正值,凡与规定正方向相反的矢量在公式中取负值。因此,应先规定正方向。(一般以V0的方向为正方向,则对于匀加速直线运动,加速度取正值;对于匀减速直线运动,加速度取负值。)
(4)统一国际单位制。
好啦!同学们,搞清楚了上面这些之后,我们一起来实践实践,解决一些实际问题。
板书:
三、 速度表达式的简单应用
例1:汽车以40km/h的速度匀速行驶,现以0.6m/s2的加速度加速,10s后的速度能达到多少?
解:选取初速度方向为x轴正方向建立直线坐标系。
初速度v0=40km/h=11m/s,加速度a=0.6m/s2,时间t=10s,10s后的速度为v,则:
v=v0+at
=11m/s+0.6m/s2×10s
=17m/s=61km/h
例题2:某汽车在紧急刹车时加速度的大小是6m/s2,如果必须在2s内停下来,汽车的行驶速度最高不能超过多少?
解:选取初速度方向为正方向建立直线坐标系。
加速度a= -6m/s2,时间t=2s,2s末的速度v=0,根据v=v0+at我们有初速度,则:
v0=v-at
=0-(-0.6m/s2)×2s
=12m/s
=43km/h
同学们,我们今天都在和图象交流、对话,接下来,请同学们看到P35的“说一说”,思考和讨论以下问题:
思考与讨论四(如果时间紧迫可以略讲,引导学生看教材)
1、如图图四是一个物体运动的v-t图象,它的速度怎样变化?
(随时间逐渐增加)
2、在相等的时间间隔内(),速度的变化量(与)总是相等吗?
(不相等, 不变,越来越小,也越来越小)
3、物体在做匀变速直线运动吗?
(物体做加速度逐渐减小的加速直线运动)
显然,这个图象长得不像我们所说的匀变速直线运动的样子,它描述的是物体做加速度逐渐减小的加速直线运动,不是我们刚才所说的匀变速直线运动。所以,从图象研究运动情况是:长相决定命运;如果从运动情况来探究图象则为:命运决定长相。
有的同学也许会问:它怎么就是“物体做加速度逐渐减小的加速直线运动“呢?图象上明明就是弯的嘛!应该是做加速度逐渐减小的曲线运动才对。同学们,请注意!看看它的坐标是什么?速度和时间,它描述的速度v与时间t的关系,不是物体运动的轨迹。所以这就提醒我们,看问题不要光看外表,要透过现象去探究本质。(看人也一样)。
课堂小结
1、匀变速直线运动
沿着一条直线,且加速度不变的运动叫做匀变速直线运动。匀变速直线运动的v-t图象是一条倾斜的直线。
2、匀变速直线运动的速度与时间的关系
图像描述:匀变速直线运动的v-t图象是一条倾斜的直线。速度随时间均匀变化。
公式表述:v=v0+at
3、在运用速度公式解题时要注意公式的矢量性
布置作业
1、课本P36《问题与练习》T2、T4(作业本上交);
2、三维设计对应的内容;
3、报纸对应的内容。
今天的故事就讲到这里,欲知后事如何,且听下回分解,下课,同学们再见!
板书设计
一 、匀变速直线运动
1、定义:沿着一条直线,且加速度不变的运动,叫做匀变速直线运动。
2、v-t图象:匀变速直线运动的v-t图象是一条倾斜的直线。
3、分类
(1)匀加速直线运动:物体的速度随时间均匀地增加;(初速度v0与加速度a同向)
(2)匀减速直线运动:物体的速度随时间均匀地减小。(初速度v0与加速度a反向)
二、速度与时间的关系式
1、表达式:
2、理解
3、讨论(时间不够可以省略):
4、注意(强调)
三、 速度表达式的简单应用
课后反思与修改
同课章节目录
- 第一章 运动的描述
- 绪论
- 1 质点 参考系和坐标系
- 2 时间和位移
- 3 运动快慢的描述──速度
- 4 实验:用打点计时器测速度
- 5 速度变化快慢的描述──加速度
- 第二章 匀变速直线运动的研究
- 1 实验:探究小车速度随时间变化的规律
- 2 匀变速直线运动的速度与时间的关系
- 3 匀变速直线运动的位移与时间的关系
- 4 匀变速直线运动的位移与速度的关系
- 5 自由落体运动
- 6 伽利略对自由落体运动的研究
- 第三章 相互作用
- 1 重力 基本相互作用
- 2 弹力
- 3 摩擦力
- 4 力的合成
- 5 力的分解
- 第四章 牛顿运动定律
- 1 牛顿第一定律
- 2 实验:探究加速度与力、质量的关系
- 3 牛顿第二定律
- 4 力学单位制
- 5 牛顿第三定律
- 6 用牛顿定律解决问题(一)
- 7 用牛顿定律解决问题(二)
