山东省东营市垦利区2021-2022学年六年级下学期期末数学试题(word版含答案)
文档属性
| 名称 | 山东省东营市垦利区2021-2022学年六年级下学期期末数学试题(word版含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 801.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 鲁教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-07-07 20:28:44 | ||
图片预览



文档简介
2021—2022学年第二学期期末质量检测
六年级数学试题
(考试时间:120分钟 分值:120分)
注意事项:
1. 本试题分第Ⅰ卷和第Ⅱ卷两部分,第Ⅰ卷为选择题,30分;第Ⅱ卷为非选择题,90分;全卷共6页.
2. 数学试题答题卡共4页.答题前,考生务必将自己的姓名、准考证号、座号等填写在试题和答题卡上,考试结束后上交答题卡.
3. 第Ⅰ卷每题选出答案后,都必须用2B铅笔把答题卡上对应题目的答案标号【ABCD】涂黑.第Ⅱ卷按要求用0.5mm碳素笔答在答题卡的相应位置上.
第Ⅰ卷(选择题 共30分)
一、选择题(本题共10小题,共30分,在每小题给出的四个选项中,只有一项是正确的,请把正确的选项选出来.每小题选对得3分,不选或选出的答案超过一个均记零分.)
1. 下列统计图能够显示数据变化趋势的是( )
A. 条形图 B. 扇形图 C. 折线图 D. 直方图
2. 如图,木工师傅过木板上的,两点,弹出一条笔直的墨线,这种操作所蕴含的数学原理是( )
A. 过一点有无数条直线 B. 两点确定一条直线
C. 两点之间线段最短 D. 线段是直线的一部分
3. 下列运算正确的是( )
A. B.
C. D.
4. 如图,海上有两艘军舰和,由测得的方向是( )
A. 北偏西 B. 北偏西 C. 南偏东 D. 南偏东
5. 已知,,,那么,,的大小关系为( )
A. B. C. D.
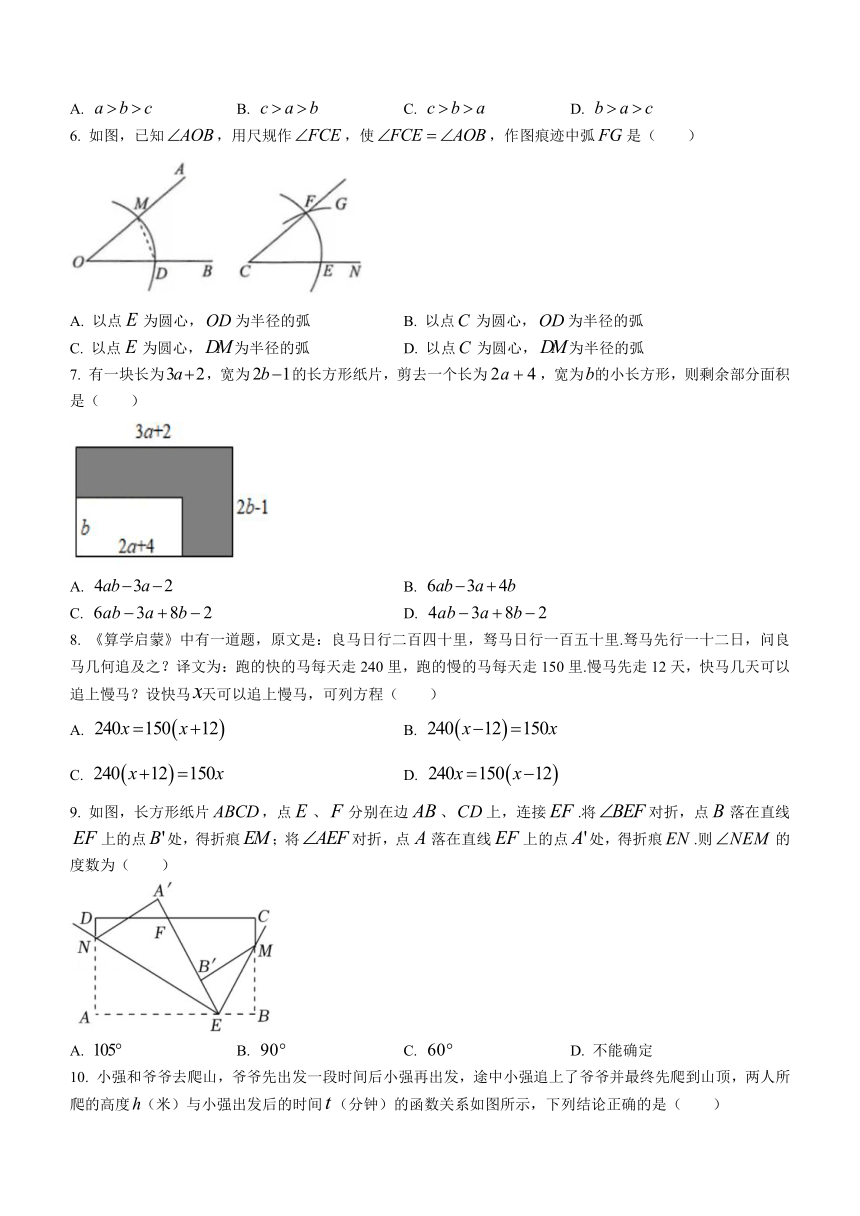
6. 如图,已知,用尺规作,使,作图痕迹中弧是( )
A. 以点为圆心,为半径的弧 B. 以点为圆心,为半径的弧
C. 以点为圆心,为半径的弧 D. 以点为圆心,为半径的弧
7. 有一块长为,宽为的长方形纸片,剪去一个长为,宽为的小长方形,则剩余部分面积是( )
A. B.
C. D.
8. 《算学启蒙》中有一道题,原文是:良马日行二百四十里,驽马日行一百五十里.驽马先行一十二日,问良马几何追及之?译文为:跑的快的马每天走240里,跑的慢的马每天走150里.慢马先走12天,快马几天可以追上慢马?设快马天可以追上慢马,可列方程( )
A. B.
C. D.
9. 如图,长方形纸片,点、分别在边、上,连接.将对折,点落在直线上的点处,得折痕;将对折,点落在直线上的点处,得折痕.则的度数为( )
A. B. C. D. 不能确定
10. 小强和爷爷去爬山,爷爷先出发一段时间后小强再出发,途中小强追上了爷爷并最终先爬到山顶,两人所爬的高度(米)与小强出发后的时间(分钟)的函数关系如图所示,下列结论正确的是( )
A. 表示的是爷爷爬山的情况,表示的是小强爬山的情况
B. 小强爬山的速度是爷爷的2倍
C. 爷爷比小强先出发20分钟
D. 山的高度是480米
第Ⅱ卷(非选择题 共90分)
二、填空题(本大题共8小题,其中11-14题每小题3分,15-18题每小题4分,共28分.只要求填写最后结果.)
11. 人体中某种细胞的形状可近似看成圆形,其直径约为,将0.00000216用科学记数法表示为_________.
12. 若,,则_________.
13. 如图是小新在询问了父母后绘制的去年全家的开支情况的扇形统计图,如果他家去年总开支为6万元,那么用于教育的支出为_________万元.
14. 如图,直线,相交于点,于点,,则的度数为_________.
15. 一根弹簧长,它所挂的物体质量不能超过,并且所挂的物体每增加弹簧就伸长,则挂上物体后弹簧的长度与所挂物体的质量()之间的表达式为_________.
16. 如图,,,,则的度数为_________.
17. 如图①,在长方形中,动点从点出发,以相同的速度,沿方向运动到点处停止.设点运动的路程为,的面积为,如果变量与之间的关系如图②所示,则长方形的面积为_________.
18. 在锐角内部,画出1条射线,可以画出3个锐角;画出2条不同的射线,可以画出6个锐角;画出3条不同的射线,可以画出10个锐角…照此规律,画9条不同的射线,可以画出_________个锐角.
三、解答题(本大题共7小题,满分62分,解答要写出必要的文字说明、证明过程或演算步骤)
19.(本题满分10分,(1)题4分,(2)题6分)
(1)计算:①;
②.
(2)化简求值:①,其中,;
②,其中,.
20.(本题满分7分)
光线在不同介质中的传播速度不同,从一种介质射向另一种介质时会发生折射.如图所示,水面与水杯下沿平行,光线从水中射向空气时发生折射,光线变成,点在射线上,已知,,求的度数.
21.(本题满分8分)
为进一步推广大课间活动,某中学对已开设的篮球、立定跳远、跑步、跳绳,四种活动项目的学生喜欢情况进行调查,随机抽取了部分学生,并将调查结果绘制成图1,图2的统计图,请结合图中的信息解答下列问题.
(1)学校共抽取了多少名学生进行调查;
(2)通过计算把条形统计图补充完整;
(3)若该校共有800名学生,请你估计喜欢立定跳远和跳绳活动项目的学生共有多少名?
22.(本题满分8分)
如图表示玲玲骑自行车离家()与时间(时)之间的关系.她9时离开家,15时回到家,请根据图象回答下列问题:
(1)玲玲在_________时到达离家最远的地方,最远离家_________;
(2)她第一次休息时,离家_________,休息了_________;
(3)从11时到12时,她骑车前进了多少?
(4)她骑车返回时的平均速度是多少?
23.(本题满分8分)
阅读例题的解答过程,并解答下列各题.
例:用简便方法计算.
解:
①
②
.
(1)例题求解过程中,第②步变形的依据是_________;
(2)用简便方法计算;
(3)用简便方法计算.
24.(本题满分10分)
如图所示,点在线段上,点,分别为,的中点.
(1)若,,求线段,的长;
(2)若点在线段的延长线上,且满足,点,分别是线段,的中点,请画出图形,并用的式子表示的长度.
25.(本题满分11分)
盲盒近来火爆,这种不确定的“盲抽”模式受到了大家的喜爱,某玩具商店计划采购文具盲盒和Molly盲盒,计划采购两种盲盒共125盒,这两种盲盒的进价、售价如下表:
类型 进价(元/盒) 售价(元/盒)
文具盲盒 16 20
Molly盲盒 36 52
(1)若采购共用去4000元,则两种盲盒各采购了多少盒?
(2)在(1)的条件下全部售完这125盒,那么玩具商店获利多少元?
(3)销售完这125个盲盒的总利润能否恰好为1600元?若能,请说出采购方案;若不能,说明理由.
六年级数学试题参考答案及评分标准
评卷说明:
1.选择题和填空题中的每小题,只有满分和零分两个评分档,不给中间分.
2.解答题中的每小题的解答中所对应的分数,是指考生正确解答到该步骤所应得的累计分数.本答案对每小题只给出一种解法,对考生的其他解法,请参照评分标准相应评分.
3.如果考生在解答的中间过程出现计算错误,但并没有改变试题的实质和难度,其后续部分酌情给分,但最多不超过正确解答分数的一半;若出现严重的逻辑错误,后续部分就不再给分.
一、选择题:本大题共10小题,共30分.每小题选对得3分,选错、不选或选出的答案超过一个均记零分.
题号 1 2 3 4 5 6 7 8 9 10
答案 C B C D D C A A B B
二、填空题:本大题共8小题,其中11-14题每小题3分,15-18题每小题4分,共28分.只要求填写最后结果.
11. 12. 2 13. 2 14.
15. 16. 17. 15 18. 55
三、解答题:本大题共7小题,共62分.解答要写出必要的文字说明、证明过程或演算步骤.
19.(本题满分10分)
解:(1)①原式;
②原式.
(2)①解:原式,
当,时,
原式.
②解:原式
,
当,时,
原式.
20.(本题满分7分)
解:∵,
∴,
∵,
∴,
∴的度数为.
21.(本题满分8分)
解:(1)根据题意得:(名).
答:学校共抽取了150名学生进行调查;
(2)本项调查中喜欢“跑步”的学生人数是:(名),
补全条形图如下:
(3)(名),
答:估计全校喜欢立定跳远和跳绳活动项目的学生共有400名.
22.(本题满分8分)
解:(1)12,30;
(2)17.5,0.5;
(3)
答:她骑车前进了.
(4)
答:她返回时的平均速度是.
23.(本题满分8分)
(1)平方差公式;
(2)解:
;
(3)解:
.
24.(本题满分10分)
解:(1)∵点是的中点,,
∴,
∵,
∴,
又∵点为的中点,
∴,
∴.
(2)如图所示:
∵点是的中点,
∴,
∵点为的中点,
∴,
∴.
25.(本题满分11分)
解:(1)设文具店分别采购文具盲盒盒,Molly盲盒盒,
由题意得,
解得,
(盒),
答:文具店采购了文具盲盒25盒,Molly盲盒100盒.
(2)(元),
答:销售完这125盒盲盒,文具店共获利1700元.
(3)设文具店分别采购文具盲盒盒,Molly盲盒盒,
由题意得,
解得,
∵为整数,∴不合题意,
答:销售完这125个盲盒的总利润不可能恰好为1600元.
六年级数学试题
(考试时间:120分钟 分值:120分)
注意事项:
1. 本试题分第Ⅰ卷和第Ⅱ卷两部分,第Ⅰ卷为选择题,30分;第Ⅱ卷为非选择题,90分;全卷共6页.
2. 数学试题答题卡共4页.答题前,考生务必将自己的姓名、准考证号、座号等填写在试题和答题卡上,考试结束后上交答题卡.
3. 第Ⅰ卷每题选出答案后,都必须用2B铅笔把答题卡上对应题目的答案标号【ABCD】涂黑.第Ⅱ卷按要求用0.5mm碳素笔答在答题卡的相应位置上.
第Ⅰ卷(选择题 共30分)
一、选择题(本题共10小题,共30分,在每小题给出的四个选项中,只有一项是正确的,请把正确的选项选出来.每小题选对得3分,不选或选出的答案超过一个均记零分.)
1. 下列统计图能够显示数据变化趋势的是( )
A. 条形图 B. 扇形图 C. 折线图 D. 直方图
2. 如图,木工师傅过木板上的,两点,弹出一条笔直的墨线,这种操作所蕴含的数学原理是( )
A. 过一点有无数条直线 B. 两点确定一条直线
C. 两点之间线段最短 D. 线段是直线的一部分
3. 下列运算正确的是( )
A. B.
C. D.
4. 如图,海上有两艘军舰和,由测得的方向是( )
A. 北偏西 B. 北偏西 C. 南偏东 D. 南偏东
5. 已知,,,那么,,的大小关系为( )
A. B. C. D.
6. 如图,已知,用尺规作,使,作图痕迹中弧是( )
A. 以点为圆心,为半径的弧 B. 以点为圆心,为半径的弧
C. 以点为圆心,为半径的弧 D. 以点为圆心,为半径的弧
7. 有一块长为,宽为的长方形纸片,剪去一个长为,宽为的小长方形,则剩余部分面积是( )
A. B.
C. D.
8. 《算学启蒙》中有一道题,原文是:良马日行二百四十里,驽马日行一百五十里.驽马先行一十二日,问良马几何追及之?译文为:跑的快的马每天走240里,跑的慢的马每天走150里.慢马先走12天,快马几天可以追上慢马?设快马天可以追上慢马,可列方程( )
A. B.
C. D.
9. 如图,长方形纸片,点、分别在边、上,连接.将对折,点落在直线上的点处,得折痕;将对折,点落在直线上的点处,得折痕.则的度数为( )
A. B. C. D. 不能确定
10. 小强和爷爷去爬山,爷爷先出发一段时间后小强再出发,途中小强追上了爷爷并最终先爬到山顶,两人所爬的高度(米)与小强出发后的时间(分钟)的函数关系如图所示,下列结论正确的是( )
A. 表示的是爷爷爬山的情况,表示的是小强爬山的情况
B. 小强爬山的速度是爷爷的2倍
C. 爷爷比小强先出发20分钟
D. 山的高度是480米
第Ⅱ卷(非选择题 共90分)
二、填空题(本大题共8小题,其中11-14题每小题3分,15-18题每小题4分,共28分.只要求填写最后结果.)
11. 人体中某种细胞的形状可近似看成圆形,其直径约为,将0.00000216用科学记数法表示为_________.
12. 若,,则_________.
13. 如图是小新在询问了父母后绘制的去年全家的开支情况的扇形统计图,如果他家去年总开支为6万元,那么用于教育的支出为_________万元.
14. 如图,直线,相交于点,于点,,则的度数为_________.
15. 一根弹簧长,它所挂的物体质量不能超过,并且所挂的物体每增加弹簧就伸长,则挂上物体后弹簧的长度与所挂物体的质量()之间的表达式为_________.
16. 如图,,,,则的度数为_________.
17. 如图①,在长方形中,动点从点出发,以相同的速度,沿方向运动到点处停止.设点运动的路程为,的面积为,如果变量与之间的关系如图②所示,则长方形的面积为_________.
18. 在锐角内部,画出1条射线,可以画出3个锐角;画出2条不同的射线,可以画出6个锐角;画出3条不同的射线,可以画出10个锐角…照此规律,画9条不同的射线,可以画出_________个锐角.
三、解答题(本大题共7小题,满分62分,解答要写出必要的文字说明、证明过程或演算步骤)
19.(本题满分10分,(1)题4分,(2)题6分)
(1)计算:①;
②.
(2)化简求值:①,其中,;
②,其中,.
20.(本题满分7分)
光线在不同介质中的传播速度不同,从一种介质射向另一种介质时会发生折射.如图所示,水面与水杯下沿平行,光线从水中射向空气时发生折射,光线变成,点在射线上,已知,,求的度数.
21.(本题满分8分)
为进一步推广大课间活动,某中学对已开设的篮球、立定跳远、跑步、跳绳,四种活动项目的学生喜欢情况进行调查,随机抽取了部分学生,并将调查结果绘制成图1,图2的统计图,请结合图中的信息解答下列问题.
(1)学校共抽取了多少名学生进行调查;
(2)通过计算把条形统计图补充完整;
(3)若该校共有800名学生,请你估计喜欢立定跳远和跳绳活动项目的学生共有多少名?
22.(本题满分8分)
如图表示玲玲骑自行车离家()与时间(时)之间的关系.她9时离开家,15时回到家,请根据图象回答下列问题:
(1)玲玲在_________时到达离家最远的地方,最远离家_________;
(2)她第一次休息时,离家_________,休息了_________;
(3)从11时到12时,她骑车前进了多少?
(4)她骑车返回时的平均速度是多少?
23.(本题满分8分)
阅读例题的解答过程,并解答下列各题.
例:用简便方法计算.
解:
①
②
.
(1)例题求解过程中,第②步变形的依据是_________;
(2)用简便方法计算;
(3)用简便方法计算.
24.(本题满分10分)
如图所示,点在线段上,点,分别为,的中点.
(1)若,,求线段,的长;
(2)若点在线段的延长线上,且满足,点,分别是线段,的中点,请画出图形,并用的式子表示的长度.
25.(本题满分11分)
盲盒近来火爆,这种不确定的“盲抽”模式受到了大家的喜爱,某玩具商店计划采购文具盲盒和Molly盲盒,计划采购两种盲盒共125盒,这两种盲盒的进价、售价如下表:
类型 进价(元/盒) 售价(元/盒)
文具盲盒 16 20
Molly盲盒 36 52
(1)若采购共用去4000元,则两种盲盒各采购了多少盒?
(2)在(1)的条件下全部售完这125盒,那么玩具商店获利多少元?
(3)销售完这125个盲盒的总利润能否恰好为1600元?若能,请说出采购方案;若不能,说明理由.
六年级数学试题参考答案及评分标准
评卷说明:
1.选择题和填空题中的每小题,只有满分和零分两个评分档,不给中间分.
2.解答题中的每小题的解答中所对应的分数,是指考生正确解答到该步骤所应得的累计分数.本答案对每小题只给出一种解法,对考生的其他解法,请参照评分标准相应评分.
3.如果考生在解答的中间过程出现计算错误,但并没有改变试题的实质和难度,其后续部分酌情给分,但最多不超过正确解答分数的一半;若出现严重的逻辑错误,后续部分就不再给分.
一、选择题:本大题共10小题,共30分.每小题选对得3分,选错、不选或选出的答案超过一个均记零分.
题号 1 2 3 4 5 6 7 8 9 10
答案 C B C D D C A A B B
二、填空题:本大题共8小题,其中11-14题每小题3分,15-18题每小题4分,共28分.只要求填写最后结果.
11. 12. 2 13. 2 14.
15. 16. 17. 15 18. 55
三、解答题:本大题共7小题,共62分.解答要写出必要的文字说明、证明过程或演算步骤.
19.(本题满分10分)
解:(1)①原式;
②原式.
(2)①解:原式,
当,时,
原式.
②解:原式
,
当,时,
原式.
20.(本题满分7分)
解:∵,
∴,
∵,
∴,
∴的度数为.
21.(本题满分8分)
解:(1)根据题意得:(名).
答:学校共抽取了150名学生进行调查;
(2)本项调查中喜欢“跑步”的学生人数是:(名),
补全条形图如下:
(3)(名),
答:估计全校喜欢立定跳远和跳绳活动项目的学生共有400名.
22.(本题满分8分)
解:(1)12,30;
(2)17.5,0.5;
(3)
答:她骑车前进了.
(4)
答:她返回时的平均速度是.
23.(本题满分8分)
(1)平方差公式;
(2)解:
;
(3)解:
.
24.(本题满分10分)
解:(1)∵点是的中点,,
∴,
∵,
∴,
又∵点为的中点,
∴,
∴.
(2)如图所示:
∵点是的中点,
∴,
∵点为的中点,
∴,
∴.
25.(本题满分11分)
解:(1)设文具店分别采购文具盲盒盒,Molly盲盒盒,
由题意得,
解得,
(盒),
答:文具店采购了文具盲盒25盒,Molly盲盒100盒.
(2)(元),
答:销售完这125盒盲盒,文具店共获利1700元.
(3)设文具店分别采购文具盲盒盒,Molly盲盒盒,
由题意得,
解得,
∵为整数,∴不合题意,
答:销售完这125个盲盒的总利润不可能恰好为1600元.
同课章节目录
