2022--2023学年沪教版九年级数学上册 24.5 相似三角形性质一 课件(共14张PPT)
文档属性
| 名称 | 2022--2023学年沪教版九年级数学上册 24.5 相似三角形性质一 课件(共14张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 162.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-07-07 18:32:48 | ||
图片预览





文档简介
(共14张PPT)
相似三角形的性质一
1)相似三角形的判定方法:
预备定理
AA定理.
SAS定理.
SSS定理.
HL定理.
相似的传递性
2)相似三角形的基本性质:
对应角相等,对应边成比例.
知识点回顾
3)全等三角形的性质:
对应角相等;
对应边相等;
③ 对应高线、中线、角平分线分别相等;
④ 周长、面积相等.
要点 :全等三角形的对应元素分别相等.
探究
已知结论:
相似 三角形的对应角相等.
相似三角形的对应边成比例.
相似三角形的对应角平分线之比等于?
相似三角形的对应中线之比等于?
相似三角形的对应高之比等于?
相似三角形的周长之比等于?
相似三角形的面积之比等于?
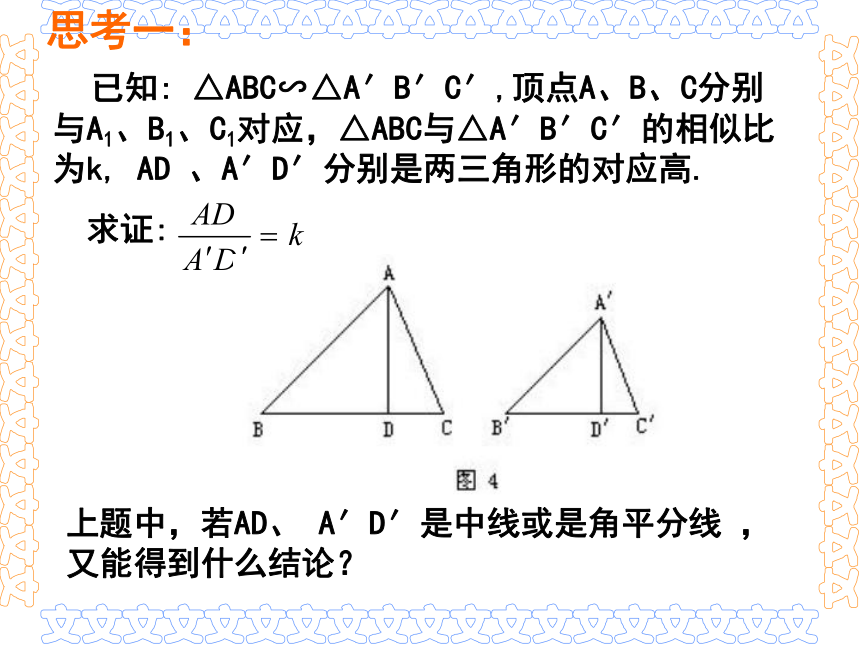
已知: △ABC∽△A′B′C′,顶点A、B、C分别与A1、B1、C1对应,△ABC与△A′B′C′的相似比为k, AD 、A′D′分别是两三角形的对应高.
求证:
上题中,若AD、 A′D′是中线或是角平分线 ,又能得到什么结论?
思考一:
性质定理一:相似三角形对应高的比、对应中线的比、对应角平分线的比都等于相似比.
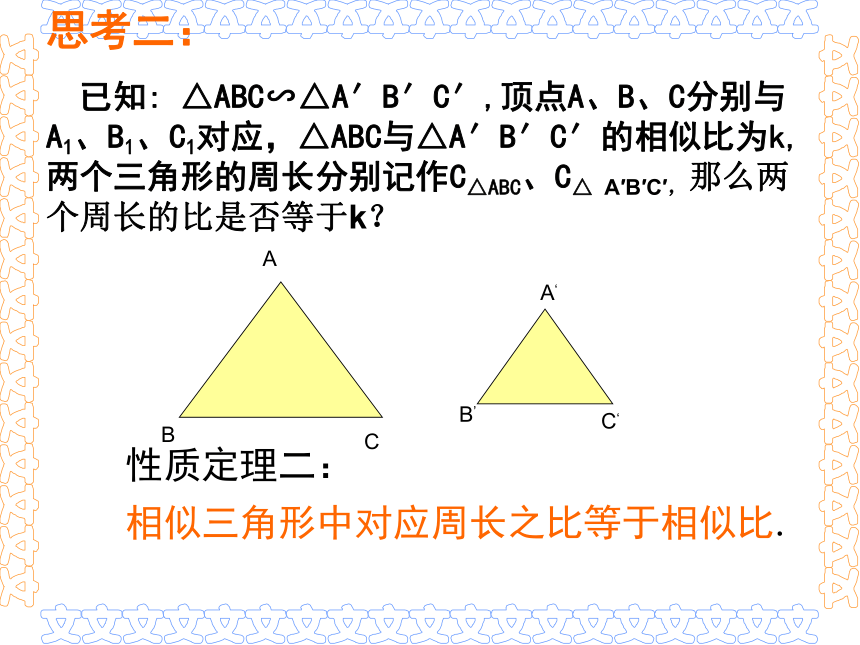
已知: △ABC∽△A′B′C′,顶点A、B、C分别与A1、B1、C1对应,△ABC与△A′B′C′的相似比为k, 两个三角形的周长分别记作C△ABC、C△ A′B′C′,那么两个周长的比是否等于k?
A
B
C
A‘
B’
C‘
性质定理二:
相似三角形中对应周长之比等于相似比.
思考二:
性质定理二:
相似三角形中对应周长之比等于相似比.
性质定理:
相似三角形中对应线段(高、角平分线、中线)及周长之比等于相似比.
性质定理一:相似三角形对应高的比、对应中线的比、对应角平分线的比都等于相似比.
已知: △ABC∽△A′B′C′,顶点A、B、C分别与A1、B1、C1对应,△ABC与△A′B′C′的相似比为k, 两个三角形的周长分别记作S△ABC、S△ A′B′C′,那么两个三角形的面积的比是否等于k?
思考三:
性质定理三:
相似三角形的面积比等于相似比的平方.
(1) 已知两相似三角形对应角平分线的比
是1∶4.求对应高的比及面积的比.
(2) 已知两相似三角形的面积比是2∶3,
求对应中线的比和周长的比.
(3) 已知:△ABC∽△A′B′C′,它们的周长分别为60cm
和72cm,AB=15cm,B′C′=24cm,
求BC,AC,A′B′, A′C′.
(4) 若 (2)中△ABC与△A′B′C′面积相差为55,
求△ABC与△A′B′C′的面积.
性质应用:
例1:在△ABC中,DE∥BC,DE和AB相交于点D,和AC相交于E,已知△ABC的面积为25、△ADE的面积为9,BC=4,求DE.
例2 △ABC与△A′B′C′中 ,AD、BE是△ABC
的两条高,A′D ′ 、B′E ′是 △A′B′C′
的两条高,且
求证:
例3 如图,C为△FDA中FA上的点,
且∠FDC=∠A.
求证:
相似三角形的性质一
1)相似三角形的判定方法:
预备定理
AA定理.
SAS定理.
SSS定理.
HL定理.
相似的传递性
2)相似三角形的基本性质:
对应角相等,对应边成比例.
知识点回顾
3)全等三角形的性质:
对应角相等;
对应边相等;
③ 对应高线、中线、角平分线分别相等;
④ 周长、面积相等.
要点 :全等三角形的对应元素分别相等.
探究
已知结论:
相似 三角形的对应角相等.
相似三角形的对应边成比例.
相似三角形的对应角平分线之比等于?
相似三角形的对应中线之比等于?
相似三角形的对应高之比等于?
相似三角形的周长之比等于?
相似三角形的面积之比等于?
已知: △ABC∽△A′B′C′,顶点A、B、C分别与A1、B1、C1对应,△ABC与△A′B′C′的相似比为k, AD 、A′D′分别是两三角形的对应高.
求证:
上题中,若AD、 A′D′是中线或是角平分线 ,又能得到什么结论?
思考一:
性质定理一:相似三角形对应高的比、对应中线的比、对应角平分线的比都等于相似比.
已知: △ABC∽△A′B′C′,顶点A、B、C分别与A1、B1、C1对应,△ABC与△A′B′C′的相似比为k, 两个三角形的周长分别记作C△ABC、C△ A′B′C′,那么两个周长的比是否等于k?
A
B
C
A‘
B’
C‘
性质定理二:
相似三角形中对应周长之比等于相似比.
思考二:
性质定理二:
相似三角形中对应周长之比等于相似比.
性质定理:
相似三角形中对应线段(高、角平分线、中线)及周长之比等于相似比.
性质定理一:相似三角形对应高的比、对应中线的比、对应角平分线的比都等于相似比.
已知: △ABC∽△A′B′C′,顶点A、B、C分别与A1、B1、C1对应,△ABC与△A′B′C′的相似比为k, 两个三角形的周长分别记作S△ABC、S△ A′B′C′,那么两个三角形的面积的比是否等于k?
思考三:
性质定理三:
相似三角形的面积比等于相似比的平方.
(1) 已知两相似三角形对应角平分线的比
是1∶4.求对应高的比及面积的比.
(2) 已知两相似三角形的面积比是2∶3,
求对应中线的比和周长的比.
(3) 已知:△ABC∽△A′B′C′,它们的周长分别为60cm
和72cm,AB=15cm,B′C′=24cm,
求BC,AC,A′B′, A′C′.
(4) 若 (2)中△ABC与△A′B′C′面积相差为55,
求△ABC与△A′B′C′的面积.
性质应用:
例1:在△ABC中,DE∥BC,DE和AB相交于点D,和AC相交于E,已知△ABC的面积为25、△ADE的面积为9,BC=4,求DE.
例2 △ABC与△A′B′C′中 ,AD、BE是△ABC
的两条高,A′D ′ 、B′E ′是 △A′B′C′
的两条高,且
求证:
例3 如图,C为△FDA中FA上的点,
且∠FDC=∠A.
求证:
