13[1].1.2平方根公开课第二课时
文档属性
| 名称 | 13[1].1.2平方根公开课第二课时 |  | |
| 格式 | zip | ||
| 文件大小 | 519.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 数学 | ||
| 更新时间 | 2013-06-25 22:29:40 | ||
图片预览






文档简介
课件28张PPT。13.1平方根(2)知识回顾:什么是算术平方根?怎样表示?如果一个正数x的平方等于a,那么这个正数x叫做a的算术平方根.0的算术平方根是0.a的算术平方根表示为:负数没有算术平方根.复习1、 的算术平方根是( )
A 4 B ±16
C 16 D ±42、 的算术平方根是( )
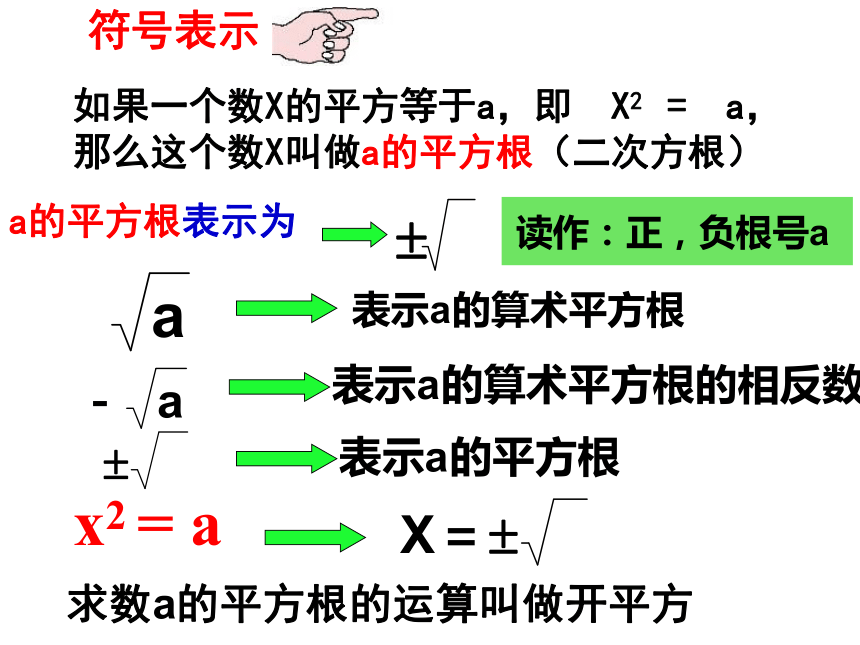
A B C D 3、面积为9的正方形的边长是 。5、如果 ,那么x = 。4、如果 ,那么x = 。AC362或3±0.8±3±4±1±6±7+1-1+4-4+6-6+7-7-+ 一般的,如果一个数的平方等于 a ,那么这个数叫作 a 的 平方根 或 二次方根 即 如果 X2 = a,那么x 叫作 a 的平方根。 求一个数a的平方根的运算叫作开平方。例如 3和-3的平方等于9,简记为±3是9的平方根被开方数a≥0如果一个数X的平方等于a,即 X2 = a,
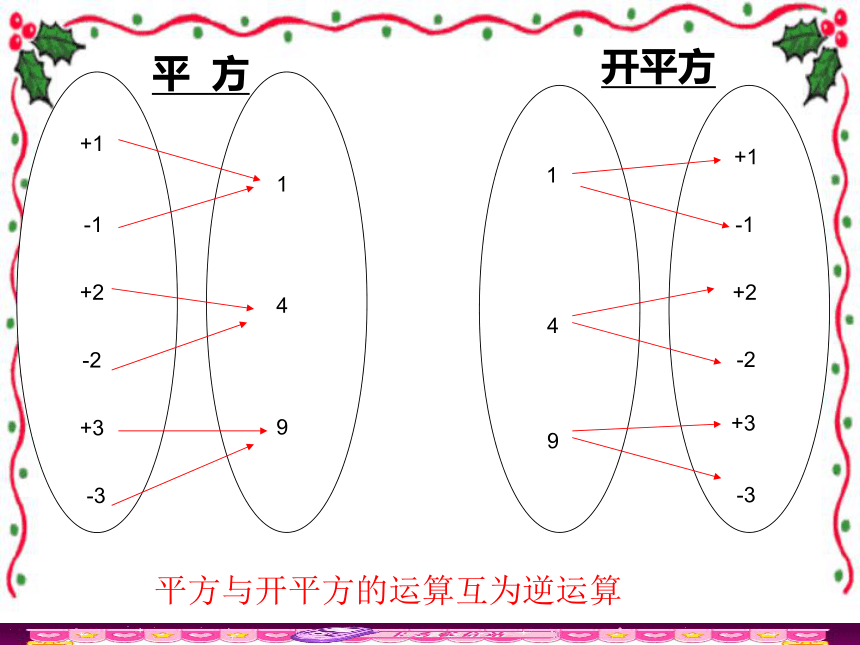
那么这个数X叫做a的平方根(二次方根)a的平方根表示为x2 = a符号表示求数a的平方根的运算叫做开平方+1-1+2-2+3-3149941-3+3-2+2-1+1平 方开平方平方与开平方的运算互为逆运算得出:( )2 = 9
( )2 =
( )2 = 0
( )2 =-4
3 2 = ( )
(-3 )2= ( )
( )2= ( )
( )2 =( )
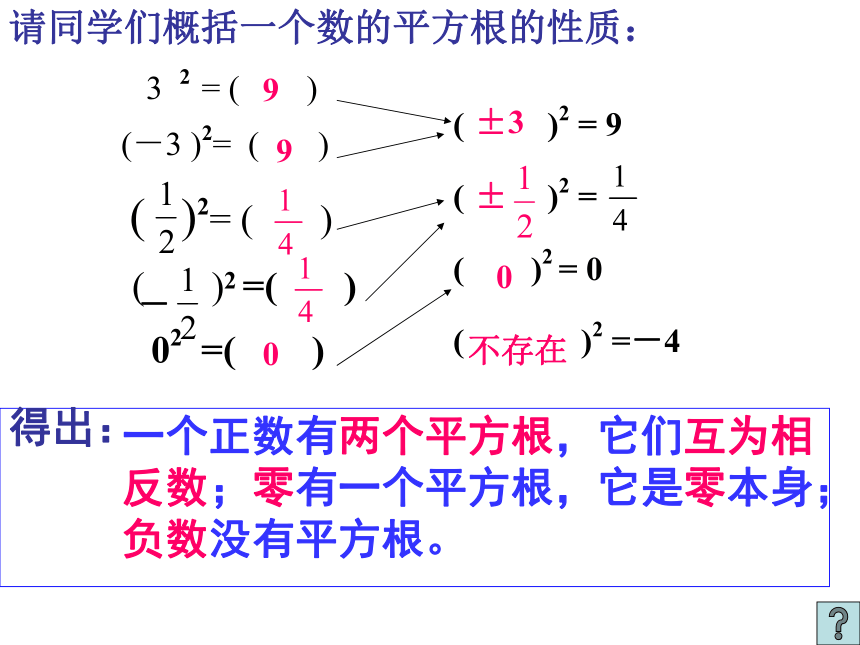
02 =( )990±3-±0不存在请同学们概括一个数的平方根的性质:一个正数有两个平方根,它们互为相
反数;零有一个平方根,它是零本身;
负数没有平方根。
正数有2个平方根,它们互为相反数;
0的平方根是0;
负数没有平方根。a的一个平方根是3,则另一个平方根是 ,a= 。-393a-22和2a-3是m的两个平方根,
试求m的值。2.计算下列各式的值:1.如果一个正数的平方根是a-1和a+3,则a=____那么这个正数是___4-1开平方:
求一个数a(a≥0)的平方根的运算,叫做开平
方,开平方运算是已知指数和幂,求底数。是不是所有的数都能进行开平方运算?不是,只有正数和零才能进行开平方运算。 由于平方与开平方互为逆运算,因此可以通过
平方运算来求一个数的平方根,也可以通过平方运
算来检验一个数是不是另一个数的平方根。
1、检验下面各题中前面的数是不是后面的数的平方根。
(1)±12 , 144 (2)±0.2 , 0.04
(3)102 ,104 (4)14 ,256
2、选择题 (1) 0.01的平方根是 ( )
(A)0.1 (B)±0.1 (C)0.0001 (D)±0.0001
(2)∵ (0.3)2 = 0.09 ∴ ( )
(A)0.09 是 0.3的平方根. (B)0.09是0.3的3倍.
(C)0.3 是0.09 的平方根. (D)0.3不是0.09的平方根.
是是是不是BC练习2:
1. 判断下列说法是否正确:
(1)-9的平方根是-3; ( )
(2)49的平方根是7 ; ( )
(3)(-2)2的平方根是±2 ;( )
(4)7是(-7)2的 算术平方根 ; ( )
(5)-1 是 1的平方根; ( )
(6)7的平方根是±49. ( )
(7)若X2 = 16 则X = 4 ( )
(8) 的平方根是±14 ( )××√√√×××判断下列说法是否正确:
(1)5是25的算术平方根
(2)5/6是25/36的一个平方根
(3)(-4)2的平方根是-4
(4)0的平方根与算术平方根都是0√×√√2. 问:3 有没有平方根 ? 若有 ,怎样表示?没有,说明为什么 ? 例1 求下列各数的平方根:(1) 100;(3) 0.25(4) (-2005)2(5)11(5)11的平方根是解: (1)∵(±10)2=100,∴100的平方根是±10, (3)∵(±0.5)2=0.25,
∴0.25的平方根是±0.5, (4)∵(±2005)2=(-2005)2,
∴(-2005)2的平方根是±2005,即1.一个正数有两个平方根,这两个平方根互为相反数。 2.零的平方根是零。3.负数没有平方根. 归纳:±1.20±±数a的平方根与数a的算术平方根有什么不同呢?数a的算术平方根就是a的正的平方根一、判断下列说法是否正确.1. 的平方根是±16. ( ) 2. 一定是正数. ( )3. a2的算术平方根是a. ( )4.若 ,则a=-5. ( )5. . ( )6. -6是(-6)2的平方根. ( )7.若x2=36,则x= ( ) 8.如果两个数平方后相等,那么它们的也相等×××××√√×思考:±63±21 下列说法中不正确的个数有 ( )
①0.25的平方根是0.5
②-0.5的平方 根是-0.25
③只有正数才有平方根
④0的平方根是0A. 1个 B. 2个. C. 3个 D. 4个C2. 下列各式哪些有意义,哪些没有意义?
(1)- (2)
(3) (4)1. 已知 有意义,则x一定是 ( )
A.正数 B.负数 C.非负数 D. 非正数2.求下列各式的值D=25=-=±补充练习;±2-13256≥0-5互为相反数3、填空±5550.6-114。填空
小结:我们学习了哪些内容,你能回答吗?1.平方根的概念:一个数的平方等于a,这个数叫做a的平方根.2.平方根的性质:一个正数的平方根有两个,它们互为相反数.0的平方根还是0.负数没有平方根.3.平方根的表示法:4.算术平方根的概念:正数a的正的平方根叫做a的算术平方根例4. 求使 有意义x的取值范围.例5.已知a、b满足等式 +︱b+5︱=0, 求a2-12b的算术平方根.再见
A 4 B ±16
C 16 D ±42、 的算术平方根是( )
A B C D 3、面积为9的正方形的边长是 。5、如果 ,那么x = 。4、如果 ,那么x = 。AC362或3±0.8±3±4±1±6±7+1-1+4-4+6-6+7-7-+ 一般的,如果一个数的平方等于 a ,那么这个数叫作 a 的 平方根 或 二次方根 即 如果 X2 = a,那么x 叫作 a 的平方根。 求一个数a的平方根的运算叫作开平方。例如 3和-3的平方等于9,简记为±3是9的平方根被开方数a≥0如果一个数X的平方等于a,即 X2 = a,
那么这个数X叫做a的平方根(二次方根)a的平方根表示为x2 = a符号表示求数a的平方根的运算叫做开平方+1-1+2-2+3-3149941-3+3-2+2-1+1平 方开平方平方与开平方的运算互为逆运算得出:( )2 = 9
( )2 =
( )2 = 0
( )2 =-4
3 2 = ( )
(-3 )2= ( )
( )2= ( )
( )2 =( )
02 =( )990±3-±0不存在请同学们概括一个数的平方根的性质:一个正数有两个平方根,它们互为相
反数;零有一个平方根,它是零本身;
负数没有平方根。
正数有2个平方根,它们互为相反数;
0的平方根是0;
负数没有平方根。a的一个平方根是3,则另一个平方根是 ,a= 。-393a-22和2a-3是m的两个平方根,
试求m的值。2.计算下列各式的值:1.如果一个正数的平方根是a-1和a+3,则a=____那么这个正数是___4-1开平方:
求一个数a(a≥0)的平方根的运算,叫做开平
方,开平方运算是已知指数和幂,求底数。是不是所有的数都能进行开平方运算?不是,只有正数和零才能进行开平方运算。 由于平方与开平方互为逆运算,因此可以通过
平方运算来求一个数的平方根,也可以通过平方运
算来检验一个数是不是另一个数的平方根。
1、检验下面各题中前面的数是不是后面的数的平方根。
(1)±12 , 144 (2)±0.2 , 0.04
(3)102 ,104 (4)14 ,256
2、选择题 (1) 0.01的平方根是 ( )
(A)0.1 (B)±0.1 (C)0.0001 (D)±0.0001
(2)∵ (0.3)2 = 0.09 ∴ ( )
(A)0.09 是 0.3的平方根. (B)0.09是0.3的3倍.
(C)0.3 是0.09 的平方根. (D)0.3不是0.09的平方根.
是是是不是BC练习2:
1. 判断下列说法是否正确:
(1)-9的平方根是-3; ( )
(2)49的平方根是7 ; ( )
(3)(-2)2的平方根是±2 ;( )
(4)7是(-7)2的 算术平方根 ; ( )
(5)-1 是 1的平方根; ( )
(6)7的平方根是±49. ( )
(7)若X2 = 16 则X = 4 ( )
(8) 的平方根是±14 ( )××√√√×××判断下列说法是否正确:
(1)5是25的算术平方根
(2)5/6是25/36的一个平方根
(3)(-4)2的平方根是-4
(4)0的平方根与算术平方根都是0√×√√2. 问:3 有没有平方根 ? 若有 ,怎样表示?没有,说明为什么 ? 例1 求下列各数的平方根:(1) 100;(3) 0.25(4) (-2005)2(5)11(5)11的平方根是解: (1)∵(±10)2=100,∴100的平方根是±10, (3)∵(±0.5)2=0.25,
∴0.25的平方根是±0.5, (4)∵(±2005)2=(-2005)2,
∴(-2005)2的平方根是±2005,即1.一个正数有两个平方根,这两个平方根互为相反数。 2.零的平方根是零。3.负数没有平方根. 归纳:±1.20±±数a的平方根与数a的算术平方根有什么不同呢?数a的算术平方根就是a的正的平方根一、判断下列说法是否正确.1. 的平方根是±16. ( ) 2. 一定是正数. ( )3. a2的算术平方根是a. ( )4.若 ,则a=-5. ( )5. . ( )6. -6是(-6)2的平方根. ( )7.若x2=36,则x= ( ) 8.如果两个数平方后相等,那么它们的也相等×××××√√×思考:±63±21 下列说法中不正确的个数有 ( )
①0.25的平方根是0.5
②-0.5的平方 根是-0.25
③只有正数才有平方根
④0的平方根是0A. 1个 B. 2个. C. 3个 D. 4个C2. 下列各式哪些有意义,哪些没有意义?
(1)- (2)
(3) (4)1. 已知 有意义,则x一定是 ( )
A.正数 B.负数 C.非负数 D. 非正数2.求下列各式的值D=25=-=±补充练习;±2-13256≥0-5互为相反数3、填空±5550.6-114。填空
小结:我们学习了哪些内容,你能回答吗?1.平方根的概念:一个数的平方等于a,这个数叫做a的平方根.2.平方根的性质:一个正数的平方根有两个,它们互为相反数.0的平方根还是0.负数没有平方根.3.平方根的表示法:4.算术平方根的概念:正数a的正的平方根叫做a的算术平方根例4. 求使 有意义x的取值范围.例5.已知a、b满足等式 +︱b+5︱=0, 求a2-12b的算术平方根.再见
