2022-2023学年人教版2019物理必修1 第三章 5 第2课时 多力平衡问题(学案+课时练 word版含解析)
文档属性
| 名称 | 2022-2023学年人教版2019物理必修1 第三章 5 第2课时 多力平衡问题(学案+课时练 word版含解析) |

|
|
| 格式 | docx | ||
| 文件大小 | 839.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(2019) | ||
| 科目 | 物理 | ||
| 更新时间 | 2022-07-07 16:34:50 | ||
图片预览



文档简介
第2课时 多力平衡问题
[学习目标] 1.知道在多力平衡中建立坐标系的原则.2.会用正交分解法分析平衡问题.
1.当物体受到不在同一条直线上的多个共点力时,一般要采用正交分解法.
2.用正交分解法解决平衡问题的一般步骤.
(1)对物体受力分析.
(2)建立坐标系:使尽可能多的力落在x、y轴上,这样需要分解的力比较少,计算方便.
(3)根据共点力平衡的条件列方程:Fx=0,Fy=0.
例1 如图,一质量m=6 kg的物块,置于水平地面上,物块与地面间的动摩擦因数μ=,为了使物块沿水平地面做匀速直线运动,现用一与水平方向夹角为37°的力斜向上拉物块,求此拉力的大小.(已知sin 37°=0.6,cos 37°=0.8,g取10 m/s2)
答案 20 N
解析 物块做匀速直线运动,受力分析如图,则
水平方向:FTcos 37°=Ff
竖直方向:FN=mg-FTsin 37°
且Ff=μFN
代入数据解得FT=20 N.
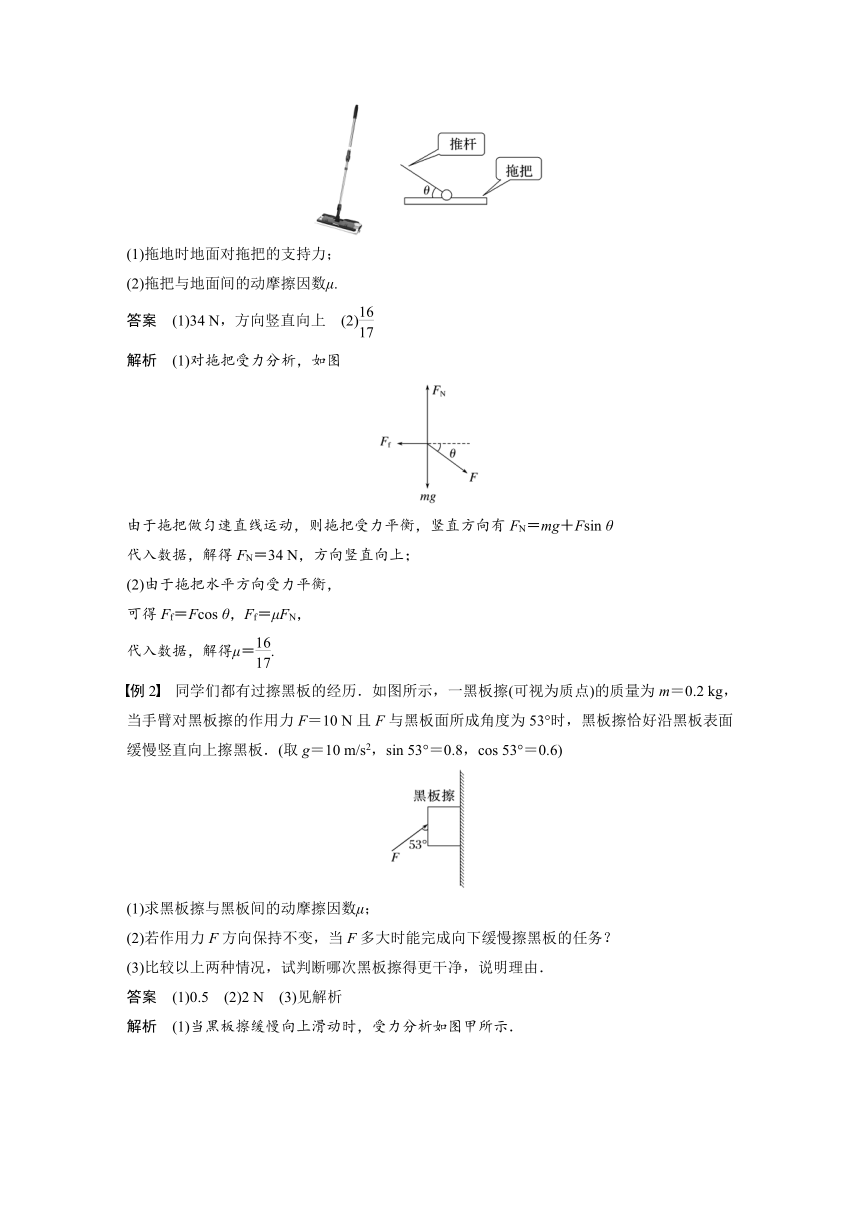
针对训练 (2021·北京北师大二附中高一期末)小王同学在家卫生大扫除时用拖把拖地,依靠拖把对地面的摩擦力来清扫污渍.如图所示,他沿推杆方向对拖把施加40 N的推力,且推杆与水平方向的夹角θ=37°时,刚好可以匀速推动拖把.已知拖把质量为1 kg,g取10 m/s2,sin 37°=0.6,cos 37°=0.8,求:
(1)拖地时地面对拖把的支持力;
(2)拖把与地面间的动摩擦因数μ.
答案 (1)34 N,方向竖直向上 (2)
解析 (1)对拖把受力分析,如图
由于拖把做匀速直线运动,则拖把受力平衡,竖直方向有FN=mg+Fsin θ
代入数据,解得FN=34 N,方向竖直向上;
(2)由于拖把水平方向受力平衡,
可得Ff=Fcos θ,Ff=μFN,
代入数据,解得μ=.
例2 同学们都有过擦黑板的经历.如图所示,一黑板擦(可视为质点)的质量为m=0.2 kg,当手臂对黑板擦的作用力F=10 N且F与黑板面所成角度为53°时,黑板擦恰好沿黑板表面缓慢竖直向上擦黑板.(取g=10 m/s2,sin 53°=0.8,cos 53°=0.6)
(1)求黑板擦与黑板间的动摩擦因数μ;
(2)若作用力F方向保持不变,当F多大时能完成向下缓慢擦黑板的任务?
(3)比较以上两种情况,试判断哪次黑板擦得更干净,说明理由.
答案 (1)0.5 (2)2 N (3)见解析
解析 (1)当黑板擦缓慢向上滑动时,受力分析如图甲所示.
根据共点力的平衡条件可知
水平方向:FN=Fsin 53°
竖直方向:Fcos 53°=Ff+mg
又因为:Ff=μFN,
联立解得μ=0.5
(2)在黑板擦缓慢向下擦的过程中,以黑板擦为研究对象进行受力分析,如图乙所示
同理可知,水平方向:FN′=F′sin 53°
竖直方向:F′cos 53°+Ff′=mg
又因为:Ff′=μFN′
解得F′=2 N
(3)由(1)(2)可知,缓慢向上移动时摩擦力比缓慢向下移动时摩擦力更大,擦得更干净.
例3 如图,在倾角为37°的固定斜面上,一质量为10 kg的物块恰好沿斜面匀速下滑,重力加速度g=10 m/s2,sin 37°=0.6,cos 37°=0.8,求:
(1)物块与斜面间的动摩擦因数μ;
(2)若用平行于斜面向上的力拉着物块沿斜面匀速上滑,求拉力F的大小.
答案 (1)0.75 (2)120 N
解析 (1)对物块受力分析,由平衡条件知
Ff=mgsin 37°,FN=mgcos 37°,Ff=μFN
联立解得μ=tan 37°=0.75
(2)F=mgsin 37°+Ff′.Ff′=μmgcos 37°
解得F=120 N.
例4 如图所示,质量为m=4 kg的物体在水平恒力F=26 N的作用下静止于斜面上,斜面的倾角θ=37°,求:(sin 37°=0.6,cos 37°=0.8,g=10 m/s2)
(1)物体受到斜面的支持力大小;
(2)物体受到的摩擦力大小.
答案 (1)47.6 N (2)3.2 N
解析 (1)对物体受力分析如图,正交分解各力有:
G1=mgsin θ=24 N
G2=mgcos θ=32 N
F1=Fcos θ=20.8 N
F2=Fsin θ=15.6 N
则斜面对物体的支持力大小:
FN=G2+F2=47.6 N
(2)因为G1>F1,故物体受到的摩擦力方向沿斜面向上,
故摩擦力大小为:Ff=G1-F1=3.2 N.
1.如图所示,某工人正在修理草坪,推力F与水平方向成α角,割草机沿水平方向做匀速直线运动,则割草机所受阻力的大小为( )
A.Fsin α B.Fcos α
C. D.
答案 B
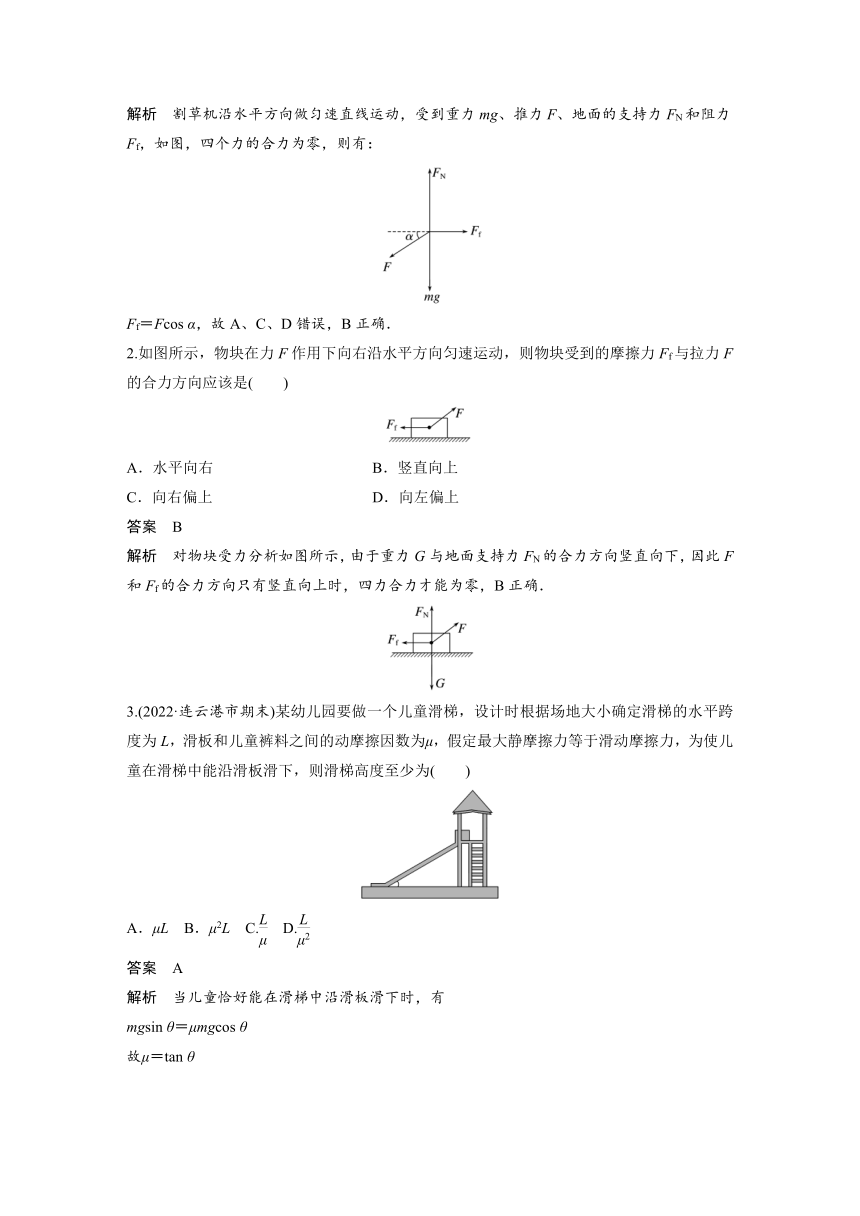
解析 割草机沿水平方向做匀速直线运动,受到重力mg、推力F、地面的支持力FN和阻力Ff,如图,四个力的合力为零,则有:
Ff=Fcos α,故A、C、D错误,B正确.
2.如图所示,物块在力F作用下向右沿水平方向匀速运动,则物块受到的摩擦力Ff与拉力F的合力方向应该是( )
A.水平向右 B.竖直向上
C.向右偏上 D.向左偏上
答案 B
解析 对物块受力分析如图所示,由于重力G与地面支持力FN的合力方向竖直向下,因此F和Ff的合力方向只有竖直向上时,四力合力才能为零,B正确.
3.(2022·连云港市期末)某幼儿园要做一个儿童滑梯,设计时根据场地大小确定滑梯的水平跨度为L,滑板和儿童裤料之间的动摩擦因数为μ,假定最大静摩擦力等于滑动摩擦力,为使儿童在滑梯中能沿滑板滑下,则滑梯高度至少为( )
A.μL B.μ2L C. D.
答案 A
解析 当儿童恰好能在滑梯中沿滑板滑下时,有
mgsin θ=μmgcos θ
故μ=tan θ
由几何关系可得tan θ=
解得H=μL,故选A.
4.(2021·淮安市六校高一上第二次学情调查)如图所示,质量为m的物体静止在水平地面上,它与地面间的动摩擦因数为μ.现将大小为F、与水平方向夹角为α的恒力作用在物体上,物体仍保持静止.重力加速度为g,则( )
A.物体所受支持力的大小为mg
B.物体所受支持力的大小为Fsin α
C.物体所受摩擦力的大小为Fcos α
D.物体所受摩擦力的大小为μmg
答案 C
5.(2022·江苏连云港高一期末)如图所示,一个质量为m的箱子,在平行于斜面的拉力F作用下,沿倾角为θ的斜面匀速上滑.已知箱子与斜面间的动摩擦因数为μ,重力加速度为g,则F的大小为( )
A.mgsin θ B.Mmgcos θ
C.mgsin θ+μmgcos θ D.mgsin θ-μmgcos θ
答案 C
解析 箱子向上匀速运动,则受力平衡,对箱子受力分析,沿斜面方向F=mgsin θ+μFN
垂直斜面方向FN=mgcos θ
解得F=mgsin θ+μmgcos θ,故选C.
6.(2021·江苏高邮高一期中)如图甲所示为冰壶运动,属于冬奥会比赛项目.现对运动员推动冰壶滑行过程建立如图乙所示模型:冰壶质量m=14.8 kg,运动员施加的推力F=20 N,方向与水平方向夹角θ=37°,g取10 m/s2,sin 37°=0.6:
(1)求推力F沿水平方向的分力的大小;
(2)若冰壶在推力F作用下做匀速直线运动,求冰壶与冰面间的动摩擦因数μ.
答案 (1)16 N (2)0.1
解析 (1)对冰壶受力分析知,F的水平分力为
Fx=Fcos 37°=16 N
(2)根据平衡条件有Ff=Fcos 37°
FN=Fsin 37°+mg,Ff=μFN
解得μ=0.1.
7.如图所示,建筑装修中,工人用质量为m的磨石对斜壁进行打磨,当对磨石施加竖直向上大小为F的推力时,磨石恰好沿斜壁向上匀速运动,已知磨石与斜壁之间的动摩擦因数为μ,重力加速度为g,则磨石受到的摩擦力是( )
A.(F-mg)sin θ B.μ(F-mg)sin θ
C.μ(F-mg)cos θ D.μ(F-mg)
答案 B
解析 对磨石进行受力分析,如图所示,由平衡条件得,沿斜壁方向:Fcos θ-mgcos θ=Ff,选项A错误;垂直于斜壁方向:FN=Fsin θ-mgsin θ,故摩擦力Ff=μFN=μ(F-mg)sin θ,选项B正确,C、D错误.
8.(2021·盐城市响水中学高一期末)如图所示,质量分别为mA=1 kg、mB=0.2 kg的物块A、B,通过一根绕过光滑定滑轮的轻质细绳相连,处于静止状态,细绳与水平面的夹角α=53°.已知sin 53°=0.8,cos 53°=0.6,g=10 m/s2,则:
(1)细绳的拉力F为多大.(已知同一根细绳上拉力大小处处相等)
(2)水平面对物块A的支持力为多大.
(3)物块A受到的摩擦力Ff为多大.
答案 (1)2 N (2)8.4 N (3)1.2 N
解析 (1)以B为研究对象,物块B受到重力和细绳拉力,根据平衡条件可得
F=mBg=0.2×10 N=2 N
(2)水平面对物块A的支持力FN=mAg-Fsin α=8.4 N
(3)物块A处于平衡状态,其受到的摩擦力为
Ff=Fcos 53°=2×0.6 N=1.2 N
9.如图所示,质量为m的木块在与水平方向成α角的推力F(大小未知)作用下,沿竖直墙壁向上匀速运动.已知木块与墙壁间的动摩擦因数为μ,重力加速度为g.
(1)求推力F的大小;
(2)若将推力的方向改为竖直向上推动木块,且木块仍做匀速直线运动,则推力F′为多大.
答案 (1) (2)mg
解析 (1)以木块为研究对象,木块受到重力、支持力、推力和摩擦力作用,受力情况如图所示.
水平方向:FN=Fcos α,
竖直方向:Fsin α=mg+Ff,
又因为:Ff=μFN,
联立各式解得:F=.
(2)若将推力的方向改为竖直向上推动木块做匀速直线运动,木块只受重力和推力,根据平衡条件可得:F′=mg.
10.(2022·江苏淮安高一期末)如图所示,整个装置处于静止状态,滑轮D固定在斜面C上,连接物块A的轻绳OD段水平、DA段与斜面平行,已知物块A的质量mA=1.2 kg,物块B的质量mB=1.6 kg,轻绳OE与竖直方向的夹角以及斜面的倾角均为37°,滑轮的摩擦不计.已知物块A与斜面间的滑动摩擦力等于最大静摩擦力,重力加速度g=10 m/s2,sin 37°=0.6,cos 37°=0.8.
(1)求轻绳DA对物块A的拉力大小;
(2)求斜面C对物块A的支持力大小;
(3)若此时物块A和斜面间的摩擦力刚好达到最大静摩擦力,求物块A和斜面间的动摩擦因数.
答案 (1)12 N (2)9.6 N (3)0.5
解析 (1)对O点受力分析,水平轻绳对O点的拉力F=mBgtan 37°=12 N
即轻绳DA对A的拉力大小F=12 N
(2)对物块A,C对A的支持力
FN=mAgcos 37°=9.6 N
(3)对物块A,沿斜面方向有
F-mAgsin 37°-Ff=0
因摩擦力为最大静摩擦力,则Ff=μFN
解得μ=0.5.
11.质量m=1 kg的物块恰好能沿倾角为37°的固定斜面匀速下滑,现给物块施加与斜面成37°斜向上的拉力F,使物块沿斜面匀速上滑,如图所示.已知最大静摩擦力等于滑动摩擦力(g取10 m/s2,sin 37°=0.6,cos 37°=0.8),
(1)求拉力F的大小;
(2)若给物块施加平行于斜面向上、大小为10 N的拉力F′,求物块受到的摩擦力.
答案 (1)9.6 N (2)4 N,方向沿斜面向下
解析 (1)物块恰好沿斜面匀速下滑
物块沿斜面方向受力平衡,有
mgsin 37°=μmgcos 37°,
得:μ=0.75
物块沿斜面匀速上滑时,物块的受力情况如图甲所示
在x方向:Fcos 37°=Ff+mgsin 37°
在y方向:FN+Fsin 37°=mgcos 37°
Ff=μFN
联立解得F=9.6 N
(2)因为F′>mgsin 37°,故物块受到沿斜面向下的摩擦力,如图乙所示,
对物块受力分析
物块所受最大静摩擦力为Ffm=μmgcos 37°
因Ff′=F′-mgsin 37°<μmgcos 37°
故物块处于静止状态,
物块受到的摩擦力Ff′=F′-mgsin 37°=4 N,方向沿斜面向下.
[学习目标] 1.知道在多力平衡中建立坐标系的原则.2.会用正交分解法分析平衡问题.
1.当物体受到不在同一条直线上的多个共点力时,一般要采用正交分解法.
2.用正交分解法解决平衡问题的一般步骤.
(1)对物体受力分析.
(2)建立坐标系:使尽可能多的力落在x、y轴上,这样需要分解的力比较少,计算方便.
(3)根据共点力平衡的条件列方程:Fx=0,Fy=0.
例1 如图,一质量m=6 kg的物块,置于水平地面上,物块与地面间的动摩擦因数μ=,为了使物块沿水平地面做匀速直线运动,现用一与水平方向夹角为37°的力斜向上拉物块,求此拉力的大小.(已知sin 37°=0.6,cos 37°=0.8,g取10 m/s2)
答案 20 N
解析 物块做匀速直线运动,受力分析如图,则
水平方向:FTcos 37°=Ff
竖直方向:FN=mg-FTsin 37°
且Ff=μFN
代入数据解得FT=20 N.
针对训练 (2021·北京北师大二附中高一期末)小王同学在家卫生大扫除时用拖把拖地,依靠拖把对地面的摩擦力来清扫污渍.如图所示,他沿推杆方向对拖把施加40 N的推力,且推杆与水平方向的夹角θ=37°时,刚好可以匀速推动拖把.已知拖把质量为1 kg,g取10 m/s2,sin 37°=0.6,cos 37°=0.8,求:
(1)拖地时地面对拖把的支持力;
(2)拖把与地面间的动摩擦因数μ.
答案 (1)34 N,方向竖直向上 (2)
解析 (1)对拖把受力分析,如图
由于拖把做匀速直线运动,则拖把受力平衡,竖直方向有FN=mg+Fsin θ
代入数据,解得FN=34 N,方向竖直向上;
(2)由于拖把水平方向受力平衡,
可得Ff=Fcos θ,Ff=μFN,
代入数据,解得μ=.
例2 同学们都有过擦黑板的经历.如图所示,一黑板擦(可视为质点)的质量为m=0.2 kg,当手臂对黑板擦的作用力F=10 N且F与黑板面所成角度为53°时,黑板擦恰好沿黑板表面缓慢竖直向上擦黑板.(取g=10 m/s2,sin 53°=0.8,cos 53°=0.6)
(1)求黑板擦与黑板间的动摩擦因数μ;
(2)若作用力F方向保持不变,当F多大时能完成向下缓慢擦黑板的任务?
(3)比较以上两种情况,试判断哪次黑板擦得更干净,说明理由.
答案 (1)0.5 (2)2 N (3)见解析
解析 (1)当黑板擦缓慢向上滑动时,受力分析如图甲所示.
根据共点力的平衡条件可知
水平方向:FN=Fsin 53°
竖直方向:Fcos 53°=Ff+mg
又因为:Ff=μFN,
联立解得μ=0.5
(2)在黑板擦缓慢向下擦的过程中,以黑板擦为研究对象进行受力分析,如图乙所示
同理可知,水平方向:FN′=F′sin 53°
竖直方向:F′cos 53°+Ff′=mg
又因为:Ff′=μFN′
解得F′=2 N
(3)由(1)(2)可知,缓慢向上移动时摩擦力比缓慢向下移动时摩擦力更大,擦得更干净.
例3 如图,在倾角为37°的固定斜面上,一质量为10 kg的物块恰好沿斜面匀速下滑,重力加速度g=10 m/s2,sin 37°=0.6,cos 37°=0.8,求:
(1)物块与斜面间的动摩擦因数μ;
(2)若用平行于斜面向上的力拉着物块沿斜面匀速上滑,求拉力F的大小.
答案 (1)0.75 (2)120 N
解析 (1)对物块受力分析,由平衡条件知
Ff=mgsin 37°,FN=mgcos 37°,Ff=μFN
联立解得μ=tan 37°=0.75
(2)F=mgsin 37°+Ff′.Ff′=μmgcos 37°
解得F=120 N.
例4 如图所示,质量为m=4 kg的物体在水平恒力F=26 N的作用下静止于斜面上,斜面的倾角θ=37°,求:(sin 37°=0.6,cos 37°=0.8,g=10 m/s2)
(1)物体受到斜面的支持力大小;
(2)物体受到的摩擦力大小.
答案 (1)47.6 N (2)3.2 N
解析 (1)对物体受力分析如图,正交分解各力有:
G1=mgsin θ=24 N
G2=mgcos θ=32 N
F1=Fcos θ=20.8 N
F2=Fsin θ=15.6 N
则斜面对物体的支持力大小:
FN=G2+F2=47.6 N
(2)因为G1>F1,故物体受到的摩擦力方向沿斜面向上,
故摩擦力大小为:Ff=G1-F1=3.2 N.
1.如图所示,某工人正在修理草坪,推力F与水平方向成α角,割草机沿水平方向做匀速直线运动,则割草机所受阻力的大小为( )
A.Fsin α B.Fcos α
C. D.
答案 B
解析 割草机沿水平方向做匀速直线运动,受到重力mg、推力F、地面的支持力FN和阻力Ff,如图,四个力的合力为零,则有:
Ff=Fcos α,故A、C、D错误,B正确.
2.如图所示,物块在力F作用下向右沿水平方向匀速运动,则物块受到的摩擦力Ff与拉力F的合力方向应该是( )
A.水平向右 B.竖直向上
C.向右偏上 D.向左偏上
答案 B
解析 对物块受力分析如图所示,由于重力G与地面支持力FN的合力方向竖直向下,因此F和Ff的合力方向只有竖直向上时,四力合力才能为零,B正确.
3.(2022·连云港市期末)某幼儿园要做一个儿童滑梯,设计时根据场地大小确定滑梯的水平跨度为L,滑板和儿童裤料之间的动摩擦因数为μ,假定最大静摩擦力等于滑动摩擦力,为使儿童在滑梯中能沿滑板滑下,则滑梯高度至少为( )
A.μL B.μ2L C. D.
答案 A
解析 当儿童恰好能在滑梯中沿滑板滑下时,有
mgsin θ=μmgcos θ
故μ=tan θ
由几何关系可得tan θ=
解得H=μL,故选A.
4.(2021·淮安市六校高一上第二次学情调查)如图所示,质量为m的物体静止在水平地面上,它与地面间的动摩擦因数为μ.现将大小为F、与水平方向夹角为α的恒力作用在物体上,物体仍保持静止.重力加速度为g,则( )
A.物体所受支持力的大小为mg
B.物体所受支持力的大小为Fsin α
C.物体所受摩擦力的大小为Fcos α
D.物体所受摩擦力的大小为μmg
答案 C
5.(2022·江苏连云港高一期末)如图所示,一个质量为m的箱子,在平行于斜面的拉力F作用下,沿倾角为θ的斜面匀速上滑.已知箱子与斜面间的动摩擦因数为μ,重力加速度为g,则F的大小为( )
A.mgsin θ B.Mmgcos θ
C.mgsin θ+μmgcos θ D.mgsin θ-μmgcos θ
答案 C
解析 箱子向上匀速运动,则受力平衡,对箱子受力分析,沿斜面方向F=mgsin θ+μFN
垂直斜面方向FN=mgcos θ
解得F=mgsin θ+μmgcos θ,故选C.
6.(2021·江苏高邮高一期中)如图甲所示为冰壶运动,属于冬奥会比赛项目.现对运动员推动冰壶滑行过程建立如图乙所示模型:冰壶质量m=14.8 kg,运动员施加的推力F=20 N,方向与水平方向夹角θ=37°,g取10 m/s2,sin 37°=0.6:
(1)求推力F沿水平方向的分力的大小;
(2)若冰壶在推力F作用下做匀速直线运动,求冰壶与冰面间的动摩擦因数μ.
答案 (1)16 N (2)0.1
解析 (1)对冰壶受力分析知,F的水平分力为
Fx=Fcos 37°=16 N
(2)根据平衡条件有Ff=Fcos 37°
FN=Fsin 37°+mg,Ff=μFN
解得μ=0.1.
7.如图所示,建筑装修中,工人用质量为m的磨石对斜壁进行打磨,当对磨石施加竖直向上大小为F的推力时,磨石恰好沿斜壁向上匀速运动,已知磨石与斜壁之间的动摩擦因数为μ,重力加速度为g,则磨石受到的摩擦力是( )
A.(F-mg)sin θ B.μ(F-mg)sin θ
C.μ(F-mg)cos θ D.μ(F-mg)
答案 B
解析 对磨石进行受力分析,如图所示,由平衡条件得,沿斜壁方向:Fcos θ-mgcos θ=Ff,选项A错误;垂直于斜壁方向:FN=Fsin θ-mgsin θ,故摩擦力Ff=μFN=μ(F-mg)sin θ,选项B正确,C、D错误.
8.(2021·盐城市响水中学高一期末)如图所示,质量分别为mA=1 kg、mB=0.2 kg的物块A、B,通过一根绕过光滑定滑轮的轻质细绳相连,处于静止状态,细绳与水平面的夹角α=53°.已知sin 53°=0.8,cos 53°=0.6,g=10 m/s2,则:
(1)细绳的拉力F为多大.(已知同一根细绳上拉力大小处处相等)
(2)水平面对物块A的支持力为多大.
(3)物块A受到的摩擦力Ff为多大.
答案 (1)2 N (2)8.4 N (3)1.2 N
解析 (1)以B为研究对象,物块B受到重力和细绳拉力,根据平衡条件可得
F=mBg=0.2×10 N=2 N
(2)水平面对物块A的支持力FN=mAg-Fsin α=8.4 N
(3)物块A处于平衡状态,其受到的摩擦力为
Ff=Fcos 53°=2×0.6 N=1.2 N
9.如图所示,质量为m的木块在与水平方向成α角的推力F(大小未知)作用下,沿竖直墙壁向上匀速运动.已知木块与墙壁间的动摩擦因数为μ,重力加速度为g.
(1)求推力F的大小;
(2)若将推力的方向改为竖直向上推动木块,且木块仍做匀速直线运动,则推力F′为多大.
答案 (1) (2)mg
解析 (1)以木块为研究对象,木块受到重力、支持力、推力和摩擦力作用,受力情况如图所示.
水平方向:FN=Fcos α,
竖直方向:Fsin α=mg+Ff,
又因为:Ff=μFN,
联立各式解得:F=.
(2)若将推力的方向改为竖直向上推动木块做匀速直线运动,木块只受重力和推力,根据平衡条件可得:F′=mg.
10.(2022·江苏淮安高一期末)如图所示,整个装置处于静止状态,滑轮D固定在斜面C上,连接物块A的轻绳OD段水平、DA段与斜面平行,已知物块A的质量mA=1.2 kg,物块B的质量mB=1.6 kg,轻绳OE与竖直方向的夹角以及斜面的倾角均为37°,滑轮的摩擦不计.已知物块A与斜面间的滑动摩擦力等于最大静摩擦力,重力加速度g=10 m/s2,sin 37°=0.6,cos 37°=0.8.
(1)求轻绳DA对物块A的拉力大小;
(2)求斜面C对物块A的支持力大小;
(3)若此时物块A和斜面间的摩擦力刚好达到最大静摩擦力,求物块A和斜面间的动摩擦因数.
答案 (1)12 N (2)9.6 N (3)0.5
解析 (1)对O点受力分析,水平轻绳对O点的拉力F=mBgtan 37°=12 N
即轻绳DA对A的拉力大小F=12 N
(2)对物块A,C对A的支持力
FN=mAgcos 37°=9.6 N
(3)对物块A,沿斜面方向有
F-mAgsin 37°-Ff=0
因摩擦力为最大静摩擦力,则Ff=μFN
解得μ=0.5.
11.质量m=1 kg的物块恰好能沿倾角为37°的固定斜面匀速下滑,现给物块施加与斜面成37°斜向上的拉力F,使物块沿斜面匀速上滑,如图所示.已知最大静摩擦力等于滑动摩擦力(g取10 m/s2,sin 37°=0.6,cos 37°=0.8),
(1)求拉力F的大小;
(2)若给物块施加平行于斜面向上、大小为10 N的拉力F′,求物块受到的摩擦力.
答案 (1)9.6 N (2)4 N,方向沿斜面向下
解析 (1)物块恰好沿斜面匀速下滑
物块沿斜面方向受力平衡,有
mgsin 37°=μmgcos 37°,
得:μ=0.75
物块沿斜面匀速上滑时,物块的受力情况如图甲所示
在x方向:Fcos 37°=Ff+mgsin 37°
在y方向:FN+Fsin 37°=mgcos 37°
Ff=μFN
联立解得F=9.6 N
(2)因为F′>mgsin 37°,故物块受到沿斜面向下的摩擦力,如图乙所示,
对物块受力分析
物块所受最大静摩擦力为Ffm=μmgcos 37°
因Ff′=F′-mgsin 37°<μmgcos 37°
故物块处于静止状态,
物块受到的摩擦力Ff′=F′-mgsin 37°=4 N,方向沿斜面向下.
