2022-2023学年人教版2019物理必修1 第四章 专题强化 传送带模型( word版含解析)
文档属性
| 名称 | 2022-2023学年人教版2019物理必修1 第四章 专题强化 传送带模型( word版含解析) |  | |
| 格式 | docx | ||
| 文件大小 | 717.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(2019) | ||
| 科目 | 物理 | ||
| 更新时间 | 2022-07-07 16:38:25 | ||
图片预览




文档简介
传送带模型
[学习目标] 1.会对传送带上的物体进行受力分析,掌握传送带模型的一般分析方法.2.能正确解答传送带上的物体的运动问题.
1.传送带的基本类型
传送带运输是利用货物和传送带之间的摩擦力将货物运送到其他地方,有水平传送带和倾斜传送带两种基本模型.
2.传送带模型分析流程
3.注意
求解的关键在于根据物体和传送带之间的相对运动情况,确定摩擦力的大小和方向.当物体的速度与传送带的速度相等时,物体所受的摩擦力有可能发生突变,速度相等前后对摩擦力的分析是解题的关键.
一、水平传送带模型
例1 如图所示,传送带保持以v=1 m/s的速度顺时针转动.现将一定质量的煤块(可视为质点)从离传送带左端很近的A点轻轻地放上去,设煤块与传送带间的动摩擦因数μ=0.1,A、B间的距离L=2.5 m,g取10 m/s2,求:
(1)煤块从A点运动到B点所经历的时间;
(2)煤块在传送带上留下痕迹的长度.
答案 (1)3 s (2)0.5 m
解析 (1)对煤块,根据题意得a==μg=1 m/s2,当速度达到1 m/s时,所用的时间t1== s=1 s,通过的位移x1==0.5 m<2.5 m.在剩余位移x2=L-x1=2.5 m-0.5 m=2 m中,因为煤块与传送带间无摩擦力,所以煤块以1 m/s的速度随传送带做匀速运动,所用时间t2==2 s
因此煤块从A点运动到B点所经历的时间
t=t1+t2=3 s
(2)煤块在传送带上留下的痕迹为二者的相对位移,发生在二者相对运动的过程
在前1 s时间内,传送带的位移
x1′=vt1=1 m
煤块相对地面运动的位移x2′=at12=0.5 m
故煤块相对传送带的位移Δx=x1′-x2′=0.5 m.
例2 如图所示,绷紧的水平传送带足够长,始终以恒定速率v1=2 m/s沿顺时针方向运行.初速度为v2=4 m/s的小物块从与传送带等高的光滑水平地面上的A处滑上传送带,小物块与传送带之间的动摩擦因数为μ=0.2,g=10 m/s2,若从小物块滑上传送带开始计时,求:
(1)小物块在传送带上滑行的最远距离;
(2)小物块从A处出发再回到A处所用的时间.
答案 (1)4 m (2)4.5 s
解析 (1)小物块滑上传送带后开始做匀减速运动,设小物块的质量为m,
由牛顿第二定律得:μmg=ma
得a=μg=2 m/s2
因小物块在传送带上滑行至最远距离时速度为0,
由速度与位移公式得x==4 m,
由速度与时间公式得t1==2 s
(2)小物块速度减为0后,再向右做匀加速运动,
加速度为a′=μg=2 m/s2
设小物块与传送带共速所需时间为t2,
由速度与时间公式得t2==1 s
t2时间内小物块向右运动的距离
x1==1 m
最后小物块做匀速直线运动,位移x2=x-x1=3 m
匀速运动时间t3==1.5 s
所以小物块从A处出发再回到A处所用的时间t总=t1+t2+t3=4.5 s.
二、倾斜传送带模型
例3 某飞机场利用如图所示的传送带将地面上的货物运送到飞机上,传送带与地面的夹角θ=30°,传送带两端A、B的距离L=10 m,传送带以v=5 m/s的恒定速度匀速向上运动.在传送带底端A轻放上一质量m=5 kg的货物(可视为质点),货物与传送带间的动摩擦因数
μ=.求货物从A端运送到B端所需的时间.(g取10 m/s2)
答案 3 s
解析 以货物为研究对象,由牛顿第二定律得
μmgcos 30°-mgsin 30°=ma
解得a=2.5 m/s2
货物匀加速运动时间t1==2 s
货物匀加速运动位移x1=at12=5 m
又μ>tan θ
然后货物做匀速运动,运动位移
x2=L-x1=5 m
匀速运动时间t2==1 s
货物从A端运送到B端所需的时间
t=t1+t2=3 s.
例4 如图所示,倾角为37°,长为l=16 m的传送带,转动速度为v=10 m/s.在传送带顶端A处无初速度地释放一个质量为m=0.5 kg的物体(可视为质点).已知物体与传送带间的动摩擦因数μ=0.5,sin 37°=0.6,cos 37°=0.8,g取10 m/s2.求:
(1)传送带顺时针转动时,物体从顶端A滑到底端B的时间;
(2)传送带逆时针转动时,物体从顶端A滑到底端B的时间.
答案 (1)4 s (2)2 s
解析 (1)传送带顺时针转动时,物体相对传送带向下运动,则物体所受滑动摩擦力方向沿传送带向上,物体沿传送带向下做匀加速运动,根据牛顿第二定律有:
mg(sin 37°-μcos 37°)=ma
则a=gsin 37°-μgcos 37°=2 m/s2,
根据l=at2得t=4 s.
(2)传送带逆时针转动,当物体下滑速度小于传送带转动速度时,物体相对传送带向上运动,则物体所受滑动摩擦力方向沿传送带向下,设物体的加速度为a1,由牛顿第二定律得,
mgsin 37°+μmgcos 37°=ma1
则有a1=10 m/s2
设当物体运动速度等于传送带速度时经历的时间为t1,位移为x1,则有
t1== s=1 s,x1=a1t12=5 m<l=16 m
当物体运动速度等于传送带速度的瞬间,因为mgsin 37°>μmgcos 37°,则此后物体相对传送带向下运动,受到传送带向上的滑动摩擦力——摩擦力发生突变.设当物体下滑速度大于传送带转动速度时物体的加速度为a2,则a2==2 m/s2
x2=l-x1=11 m
又因为x2=vt2+a2t22,则有10t2+t22=11,
解得:t2=1 s(t2=-11 s舍去)
所以t总=t1+t2=2 s.
1.水平传送带常见类型及滑块运动情况
类型 滑块运动情况
(1)可能一直加速 (2)可能先加速后匀速
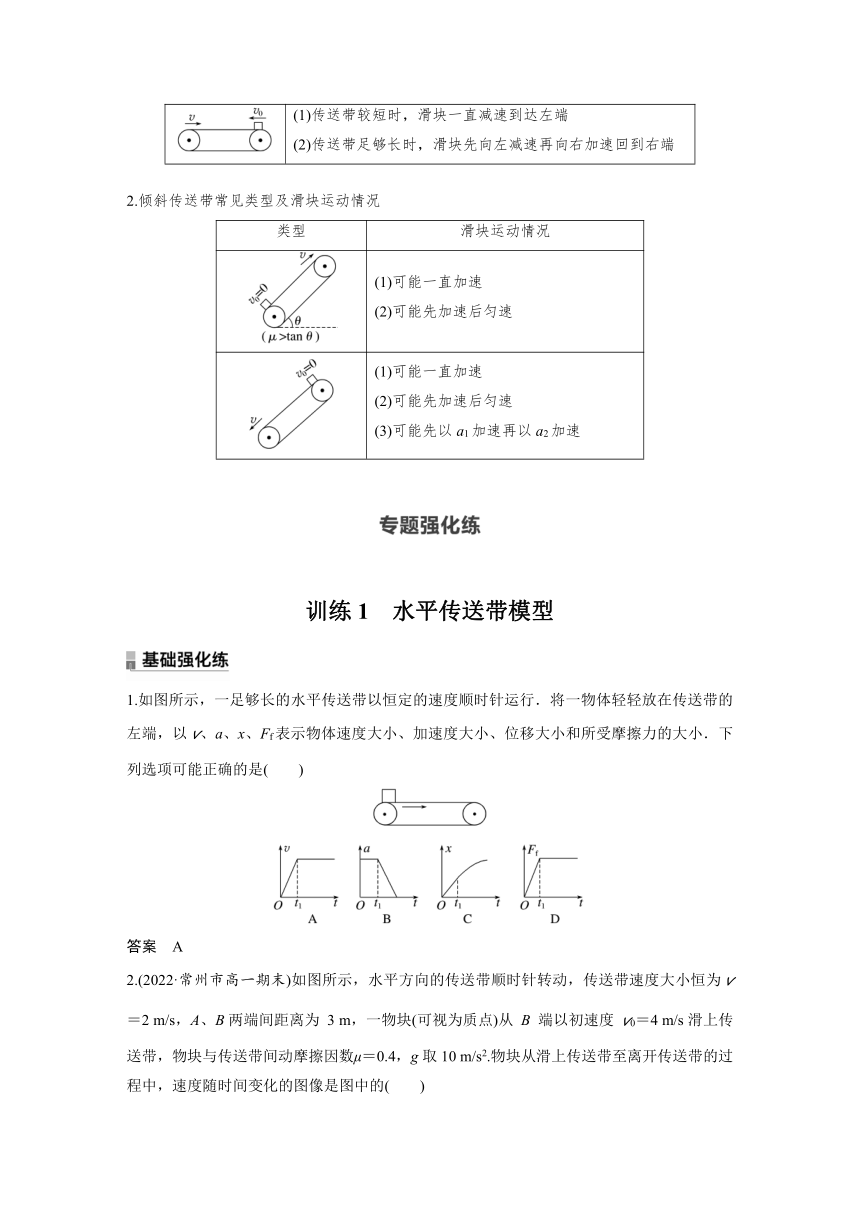
(1)v0>v时,可能一直减速,也可能先减速再匀速 (2)v0=v时,一直匀速 (3)v0(1)传送带较短时,滑块一直减速到达左端 (2)传送带足够长时,滑块先向左减速再向右加速回到右端
2.倾斜传送带常见类型及滑块运动情况
类型 滑块运动情况
(1)可能一直加速 (2)可能先加速后匀速
(1)可能一直加速 (2)可能先加速后匀速 (3)可能先以a1加速再以a2加速
训练1 水平传送带模型
1.如图所示,一足够长的水平传送带以恒定的速度顺时针运行.将一物体轻轻放在传送带的左端,以v、a、x、Ff表示物体速度大小、加速度大小、位移大小和所受摩擦力的大小.下列选项可能正确的是( )
答案 A
2.(2022·常州市高一期末)如图所示,水平方向的传送带顺时针转动,传送带速度大小恒为v=2 m/s,A、B两端间距离为 3 m,一物块(可视为质点)从 B 端以初速度 v0=4 m/s滑上传送带,物块与传送带间动摩擦因数μ=0.4,g取10 m/s2.物块从滑上传送带至离开传送带的过程中,速度随时间变化的图像是图中的( )
答案 B
3.(2022·如皋高一期末)如图所示,一火车站的传送带以0.8 m/s的速度顺时针匀速转动,传送带上表面A、B两端间的距离为2 m.旅客将行李(可视为质点)无初速度地放在A端,行李与传送带间的动摩擦因数为0.4,重力加速度g取10 m/s2,则行李从A端运动到B端的时间为( )
A.2.4 s B.2.5 s C.2.6 s D.2.8 s
答案 C
解析 开始时,行李受向右的滑动摩擦力,
根据牛顿第二定律μmg=ma
解得a=4 m/s2,设行李做匀加速运动的时间为t1,行李加速运动的末速度为v=0.8 m/s,
根据v=at1,
代入数据解得t1=0.2 s
匀加速运动的位移大小为x=t1=0.08 m
则匀速运动的时间为t2== s=2.4 s
可得行李从A端运动到B端的时间为t=t1+t2=2.6 s,故选C.
4.(2021·湖南师大附中高一上期末)如图所示,水平传送带以不变的速度v=10 m/s向右运动,将工件(可视为质点)轻轻放在传送带的左端,由于摩擦力的作用,工件做匀加速运动,经过时间t=2 s,速度达到v;再经过时间t′=4 s,工件到达传送带的右端,g取10 m/s2,求:
(1)工件在水平传送带上滑动时的加速度的大小;
(2)工件与水平传送带间的动摩擦因数;
(3)水平传送带的长度.
答案 (1)5 m/s2 (2)0.5 (3)50 m
解析 (1)工件的加速度大小a=
解得a=5 m/s2.
(2)设工件的质量为m,由牛顿第二定律得:
μmg=ma
解得动摩擦因数μ=0.5.
(3)工件匀加速运动通过的距离x1=t=10 m
工件匀速运动通过的距离x2=vt′=40 m
水平传送带长度也就是工件从左端到达右端通过的距离x=x1+x2
联立解得x=50 m.
5.(2022·钦州高一期末)如图甲,水平传送带逆时针匀速转动,一小物块以某一速度从最左端滑上传送带,取向右为正方向,从小物块滑上传送带开始计时,小物块的v-t图像(以地面为参考系)如图乙所示,g取10 m/s2,则( )
A.传送带的速度大小为2.0 m/s
B.小物块与传送带间的动摩擦因数为0.2
C.小物块相对传送带滑动的总时间为4.5 s
D.小物块相对传送带滑动的总距离为4.5 m
答案 D
解析 3.0~4.0 s物块的速度与传送带速度相等,则传送带的速度大小为1 m/s,A错误;0~2.0 s时间内物块加速度大小为a==1.0 m/s2,根据牛顿第二定律得μmg=ma,得μ=0.1,B错误;由题图乙可知,小物块相对传送带滑动的总时间为3.0 s,C错误;由于v-t图像的“面积”表示位移,0~2.0 s,小物块与传送带相向运动,2.0~3.0 s,小物块与传送带同向运动,故小物块相对传送带滑动的距离为Δx= m+ m=4.5 m,D正确.
6.如图所示为一水平传送带装置示意图.紧绷的传送带始终以恒定的速率v=1 m/s运行,一质量为m=4 kg的物体无初速度地放在A处,传送带对物体的滑动摩擦力使物体开始做匀加速直线运动,随后物体又以与传送带相等的速率做匀速直线运动.设物体与传送带之间的动摩擦因数μ=0.1,A、B间的距离L=2 m,g取10 m/s2.
(1)求物体刚开始运动时所受滑动摩擦力的大小与加速度的大小;
(2)求物体由A运动到B的时间;
(3)如果提高传送带的运行速率,物体就能被较快地传送到B处,求使物体从A处传送到B处的最短时间和传送带对应的最小运行速率.
答案 (1)4 N 1 m/s2 (2)2.5 s (3)2 s 2 m/s
解析 (1)滑动摩擦力Ff1=μmg=0.1×4×10 N=4 N,
加速度a==1 m/s2.
(2)物体匀加速运动的时间t1==1 s,
物体匀加速运动的位移x1==0.5 m.
物体匀速运动的时间t2==1.5 s
则物体由A运动到B的时间t=t1+t2=2.5 s.
(3)物体一直做匀加速运动时物体从A处传送到B处的时间最短,加速度仍为a=1 m/s2,当物体到达B处时,有vmin2=2aL,vmin== m/s=2 m/s,
所以传送带的最小运行速率为2 m/s.
设物体最短运行时间为tmin,则vmin=atmin,
得tmin== s=2 s.
7.如图,一平直的传送带以速率v=2 m/s顺时针匀速运行,在A处把物体轻轻地放到传送带上,经过6 s,物体到达B处,A、B相距L=10 m,重力加速度g=10 m/s2.则:
(1)物体在传送带上匀加速运动的时间是多少?
(2)物体与传送带之间的动摩擦因数为多少?
(3)若物体是煤块,求物体在传送带上的划痕长度.
答案 (1)2 s (2)0.1 (3)2 m
解析 (1)由题意可知,物体从A到B先做匀加速直线运动,后与传送带达到相同速度,匀速运动到B端,
设物体做匀加速运动的时间为t
所以t+v(6 s-t)=L
代入数据解得:t=2 s
(2)在匀加速运动过程中,根据牛顿第二定律可知μmg=ma
根据速度与时间的关系式得:v=at
联立解得:μ=0.1
(3)在物体匀加速运动过程中,传送带上表面相对于地面的位移x=vt=4 m
物体相对于地面的位移x′=at2=2 m
所以物体在传送带上的划痕长度Δx=x-x′=2 m.
训练2 倾斜传送带模型
1.(2022·南京高一期末)传送带被广泛地应用于机场和火车站,如图所示为倾斜传送带装置示意图,传送带足够长,木箱M在静止的传送带上以速度v匀速下滑,某时刻传送带突然顺时针以速度v1启动,则传送带启动后( )
A.木箱M开始加速上滑 B.木箱M开始减速下滑
C.木箱M继续匀速下滑 D.木箱M开始匀速上滑
答案 C
解析 木箱M在静止的传送带上以速度v匀速下滑,受力平衡,说明滑动摩擦力沿传送带向上,大小等于重力沿传送带向下的分力;传送带启动后,木箱相对传送带下滑,受沿传送带向上的滑动摩擦力,大小不变,大小仍然等于重力沿传送带向下的分力,所以木箱继续匀速下滑,故选C.
2.如图所示,足够长的传送带与水平面夹角为θ,以速度v0匀速向下运动,在传送带的上端轻轻放上一个质量为m的小木块,小木块与传送带间的动摩擦因数μ<tan θ,则下列图中能客观地反映小木块的速度随时间变化关系的是( )
答案 D
解析 开始时小木块相对传送带向后运动,滑动摩擦力沿传送带向下,则小木块的加速度为a1=gsin θ+μgcos θ
则第一阶段木块沿传送带向下做匀加速直线运动,因传送带足够长,则木块和传送带能够共速,共速时,因μ<tan θ,木块将继续加速,加速度为a2=gsin θ-μgcos θ,综上所述,木块先以a1做匀加速直线运动,后以a2做匀加速直线运动,故A、B、C错误,D正确.
3.如图,倾角θ=37°、足够长的传送带以恒定速率顺时针运行,现将一质量m=2 kg的小物体轻放在传送带的A端,小物体与传送带间的动摩擦因数μ=0.8,取g=10 m/s2,sin 37°=0.6,cos 37°=0.8,则在上升过程中的小物体( )
A.加速度恒定
B.先加速运动后匀速运动
C.所受的摩擦力方向发生变化
D.所受的摩擦力大小始终为12 N
答案 B
解析 开始时物体受到沿传送带向上的滑动摩擦力,因Ff=μmgcos 37°=12.8 N>mgsin 37°=12 N,则物体沿传送带向上加速运动,由于传送带足够长,当物体的速度与传送带的速度相等时,因μmgcos 37°>mgsin 37°,则之后物体相对传送带静止,随传送带一起匀速向上运动,物体所受静摩擦力大小为12 N,方向沿传送带向上,则选项B正确,A、C、D错误.
4.(2021·泰州中学、南菁高中高一上联考)倾斜传送带以恒定的速率沿逆时针方向运行,如图甲所示.在t=0时,将一小煤块轻放在传送带上A点处,1.5 s时小煤块从B点离开传送带.小煤块速度随时间变化的图像如图乙所示,设沿传送带向下的方向为运动的正方向,取重力加速度g=10 m/s2,不计小煤块与传送带摩擦过程中损失的质量,求:
(1)0~0.5 s内和0.5~1.5 s内小煤块的加速度大小;
(2)小煤块与传送带之间的动摩擦因数;
(3)在0~1.5 s时间内小煤块在传送带上留下的痕迹长度.
答案 见解析
解析 (1)由v-t图像得:0~0.5 s内小煤块的加速度大小a1==10 m/s2
0.5~1.5 s内小煤块的加速度大小
a2==2 m/s2
(2)对小煤块,由牛顿第二定律得:
0~0.5 s内:mgsin θ+μmgcos θ=ma1
0.5~1.5 s内:mgsin θ-μmgcos θ=ma2
联立解得μ=0.5
(3)由v-t图像知,传送带的速度为v1=5 m/s
0~0.5 s内:传送带多运动
Δx1=v1t1-v1t1=1.25 m
0.5~1.5 s内:
小煤块多运动Δx2=(v1+v2)t2-v1t2=1 m
痕迹覆盖,所以0~1.5 s时间内小煤块在传送带上留下的痕迹长度为1.25 m.
5.如图所示,传送带与水平面夹角θ=37°,两轮间距离即A、B两点间长度L=16 m,传送带以v=3 m/s的恒定速率顺时针转动.现有质量m=0.5 kg的物块以初速率v0=1 m/s由底端A处冲上传送带,已知物块与传送带之间的动摩擦因数μ=0.8,重力加速度g取10 m/s2,sin 37°=0.6,cos 37°=0.8.求:
(1)从物块冲上传送带开始计时,经6 s时物块的速度大小.
(2)物块从A运动到B所用的时间.
答案 (1)3 m/s (2)7 s
解析 (1)对物块受力分析如图所示,
由牛顿第二定律得:
μmgcos θ-mgsin θ=ma,
得a=0.4 m/s2
物块运动到与传送带相对静止所用时间
t1==5 s
物块运动的位移x1=t1=t1=10 m因μ>tan θ,所以5 s后物块随传送带一起匀速运动,故6 s时物块的速度为3 m/s
(2)物块匀速运动的位移x2=L-x1=6 m,匀速运动时间t2==2 s
物块从A运动到B所用的时间t=t1+t2=7 s.
6.如图甲所示,倾斜传送带倾角θ=37°,两端A、B间距离为L=4 m,传送带以4 m/s的速度顺时针转动.一质量为1 kg的小滑块从传送带顶端B点由静止释放,沿传送带下滑,到A时用时2 s,g取10 m/s2,sin 37°=0.6,cos 37°=0.8.
(1)求小滑块与传送带间的动摩擦因数;
(2)若该小滑块在传送带的底端A,现用一沿传送带向上的大小为6 N的恒定拉力F拉滑块,使其由静止沿传送带向上运动,当速度与传送带速度相等时,求滑块的位移大小.
(3)在第二问的条件下,求滑块从A运动到B的时间.
答案 见解析
解析 (1)当传送带顺时针转动时,对小滑块由牛顿第二定律可知:mgsin θ-μmgcos θ=ma,
根据位移公式,有L=at2
联立解得:μ=0.5.
(2)传送带的速度为v=4 m/s,当拉力F对滑块作用后,滑块开始做匀加速运动,由牛顿第二定律可得:F+μmgcos θ-mgsin θ=ma1
解得:a1=4 m/s2.
滑块加速到与传送带速度相等的过程,滑块的位移大小为x1== m=2 m,
时间为t1==1 s.
(3)滑块加速到与传送带速度相等之后,
由于F=mgsin θ,
滑块所受摩擦力突变为0,滑块与传送带相对静止,一起匀速运动t2==0.5 s
故tAB=t1+t2=1.5 s.
[学习目标] 1.会对传送带上的物体进行受力分析,掌握传送带模型的一般分析方法.2.能正确解答传送带上的物体的运动问题.
1.传送带的基本类型
传送带运输是利用货物和传送带之间的摩擦力将货物运送到其他地方,有水平传送带和倾斜传送带两种基本模型.
2.传送带模型分析流程
3.注意
求解的关键在于根据物体和传送带之间的相对运动情况,确定摩擦力的大小和方向.当物体的速度与传送带的速度相等时,物体所受的摩擦力有可能发生突变,速度相等前后对摩擦力的分析是解题的关键.
一、水平传送带模型
例1 如图所示,传送带保持以v=1 m/s的速度顺时针转动.现将一定质量的煤块(可视为质点)从离传送带左端很近的A点轻轻地放上去,设煤块与传送带间的动摩擦因数μ=0.1,A、B间的距离L=2.5 m,g取10 m/s2,求:
(1)煤块从A点运动到B点所经历的时间;
(2)煤块在传送带上留下痕迹的长度.
答案 (1)3 s (2)0.5 m
解析 (1)对煤块,根据题意得a==μg=1 m/s2,当速度达到1 m/s时,所用的时间t1== s=1 s,通过的位移x1==0.5 m<2.5 m.在剩余位移x2=L-x1=2.5 m-0.5 m=2 m中,因为煤块与传送带间无摩擦力,所以煤块以1 m/s的速度随传送带做匀速运动,所用时间t2==2 s
因此煤块从A点运动到B点所经历的时间
t=t1+t2=3 s
(2)煤块在传送带上留下的痕迹为二者的相对位移,发生在二者相对运动的过程
在前1 s时间内,传送带的位移
x1′=vt1=1 m
煤块相对地面运动的位移x2′=at12=0.5 m
故煤块相对传送带的位移Δx=x1′-x2′=0.5 m.
例2 如图所示,绷紧的水平传送带足够长,始终以恒定速率v1=2 m/s沿顺时针方向运行.初速度为v2=4 m/s的小物块从与传送带等高的光滑水平地面上的A处滑上传送带,小物块与传送带之间的动摩擦因数为μ=0.2,g=10 m/s2,若从小物块滑上传送带开始计时,求:
(1)小物块在传送带上滑行的最远距离;
(2)小物块从A处出发再回到A处所用的时间.
答案 (1)4 m (2)4.5 s
解析 (1)小物块滑上传送带后开始做匀减速运动,设小物块的质量为m,
由牛顿第二定律得:μmg=ma
得a=μg=2 m/s2
因小物块在传送带上滑行至最远距离时速度为0,
由速度与位移公式得x==4 m,
由速度与时间公式得t1==2 s
(2)小物块速度减为0后,再向右做匀加速运动,
加速度为a′=μg=2 m/s2
设小物块与传送带共速所需时间为t2,
由速度与时间公式得t2==1 s
t2时间内小物块向右运动的距离
x1==1 m
最后小物块做匀速直线运动,位移x2=x-x1=3 m
匀速运动时间t3==1.5 s
所以小物块从A处出发再回到A处所用的时间t总=t1+t2+t3=4.5 s.
二、倾斜传送带模型
例3 某飞机场利用如图所示的传送带将地面上的货物运送到飞机上,传送带与地面的夹角θ=30°,传送带两端A、B的距离L=10 m,传送带以v=5 m/s的恒定速度匀速向上运动.在传送带底端A轻放上一质量m=5 kg的货物(可视为质点),货物与传送带间的动摩擦因数
μ=.求货物从A端运送到B端所需的时间.(g取10 m/s2)
答案 3 s
解析 以货物为研究对象,由牛顿第二定律得
μmgcos 30°-mgsin 30°=ma
解得a=2.5 m/s2
货物匀加速运动时间t1==2 s
货物匀加速运动位移x1=at12=5 m
又μ>tan θ
然后货物做匀速运动,运动位移
x2=L-x1=5 m
匀速运动时间t2==1 s
货物从A端运送到B端所需的时间
t=t1+t2=3 s.
例4 如图所示,倾角为37°,长为l=16 m的传送带,转动速度为v=10 m/s.在传送带顶端A处无初速度地释放一个质量为m=0.5 kg的物体(可视为质点).已知物体与传送带间的动摩擦因数μ=0.5,sin 37°=0.6,cos 37°=0.8,g取10 m/s2.求:
(1)传送带顺时针转动时,物体从顶端A滑到底端B的时间;
(2)传送带逆时针转动时,物体从顶端A滑到底端B的时间.
答案 (1)4 s (2)2 s
解析 (1)传送带顺时针转动时,物体相对传送带向下运动,则物体所受滑动摩擦力方向沿传送带向上,物体沿传送带向下做匀加速运动,根据牛顿第二定律有:
mg(sin 37°-μcos 37°)=ma
则a=gsin 37°-μgcos 37°=2 m/s2,
根据l=at2得t=4 s.
(2)传送带逆时针转动,当物体下滑速度小于传送带转动速度时,物体相对传送带向上运动,则物体所受滑动摩擦力方向沿传送带向下,设物体的加速度为a1,由牛顿第二定律得,
mgsin 37°+μmgcos 37°=ma1
则有a1=10 m/s2
设当物体运动速度等于传送带速度时经历的时间为t1,位移为x1,则有
t1== s=1 s,x1=a1t12=5 m<l=16 m
当物体运动速度等于传送带速度的瞬间,因为mgsin 37°>μmgcos 37°,则此后物体相对传送带向下运动,受到传送带向上的滑动摩擦力——摩擦力发生突变.设当物体下滑速度大于传送带转动速度时物体的加速度为a2,则a2==2 m/s2
x2=l-x1=11 m
又因为x2=vt2+a2t22,则有10t2+t22=11,
解得:t2=1 s(t2=-11 s舍去)
所以t总=t1+t2=2 s.
1.水平传送带常见类型及滑块运动情况
类型 滑块运动情况
(1)可能一直加速 (2)可能先加速后匀速
(1)v0>v时,可能一直减速,也可能先减速再匀速 (2)v0=v时,一直匀速 (3)v0
2.倾斜传送带常见类型及滑块运动情况
类型 滑块运动情况
(1)可能一直加速 (2)可能先加速后匀速
(1)可能一直加速 (2)可能先加速后匀速 (3)可能先以a1加速再以a2加速
训练1 水平传送带模型
1.如图所示,一足够长的水平传送带以恒定的速度顺时针运行.将一物体轻轻放在传送带的左端,以v、a、x、Ff表示物体速度大小、加速度大小、位移大小和所受摩擦力的大小.下列选项可能正确的是( )
答案 A
2.(2022·常州市高一期末)如图所示,水平方向的传送带顺时针转动,传送带速度大小恒为v=2 m/s,A、B两端间距离为 3 m,一物块(可视为质点)从 B 端以初速度 v0=4 m/s滑上传送带,物块与传送带间动摩擦因数μ=0.4,g取10 m/s2.物块从滑上传送带至离开传送带的过程中,速度随时间变化的图像是图中的( )
答案 B
3.(2022·如皋高一期末)如图所示,一火车站的传送带以0.8 m/s的速度顺时针匀速转动,传送带上表面A、B两端间的距离为2 m.旅客将行李(可视为质点)无初速度地放在A端,行李与传送带间的动摩擦因数为0.4,重力加速度g取10 m/s2,则行李从A端运动到B端的时间为( )
A.2.4 s B.2.5 s C.2.6 s D.2.8 s
答案 C
解析 开始时,行李受向右的滑动摩擦力,
根据牛顿第二定律μmg=ma
解得a=4 m/s2,设行李做匀加速运动的时间为t1,行李加速运动的末速度为v=0.8 m/s,
根据v=at1,
代入数据解得t1=0.2 s
匀加速运动的位移大小为x=t1=0.08 m
则匀速运动的时间为t2== s=2.4 s
可得行李从A端运动到B端的时间为t=t1+t2=2.6 s,故选C.
4.(2021·湖南师大附中高一上期末)如图所示,水平传送带以不变的速度v=10 m/s向右运动,将工件(可视为质点)轻轻放在传送带的左端,由于摩擦力的作用,工件做匀加速运动,经过时间t=2 s,速度达到v;再经过时间t′=4 s,工件到达传送带的右端,g取10 m/s2,求:
(1)工件在水平传送带上滑动时的加速度的大小;
(2)工件与水平传送带间的动摩擦因数;
(3)水平传送带的长度.
答案 (1)5 m/s2 (2)0.5 (3)50 m
解析 (1)工件的加速度大小a=
解得a=5 m/s2.
(2)设工件的质量为m,由牛顿第二定律得:
μmg=ma
解得动摩擦因数μ=0.5.
(3)工件匀加速运动通过的距离x1=t=10 m
工件匀速运动通过的距离x2=vt′=40 m
水平传送带长度也就是工件从左端到达右端通过的距离x=x1+x2
联立解得x=50 m.
5.(2022·钦州高一期末)如图甲,水平传送带逆时针匀速转动,一小物块以某一速度从最左端滑上传送带,取向右为正方向,从小物块滑上传送带开始计时,小物块的v-t图像(以地面为参考系)如图乙所示,g取10 m/s2,则( )
A.传送带的速度大小为2.0 m/s
B.小物块与传送带间的动摩擦因数为0.2
C.小物块相对传送带滑动的总时间为4.5 s
D.小物块相对传送带滑动的总距离为4.5 m
答案 D
解析 3.0~4.0 s物块的速度与传送带速度相等,则传送带的速度大小为1 m/s,A错误;0~2.0 s时间内物块加速度大小为a==1.0 m/s2,根据牛顿第二定律得μmg=ma,得μ=0.1,B错误;由题图乙可知,小物块相对传送带滑动的总时间为3.0 s,C错误;由于v-t图像的“面积”表示位移,0~2.0 s,小物块与传送带相向运动,2.0~3.0 s,小物块与传送带同向运动,故小物块相对传送带滑动的距离为Δx= m+ m=4.5 m,D正确.
6.如图所示为一水平传送带装置示意图.紧绷的传送带始终以恒定的速率v=1 m/s运行,一质量为m=4 kg的物体无初速度地放在A处,传送带对物体的滑动摩擦力使物体开始做匀加速直线运动,随后物体又以与传送带相等的速率做匀速直线运动.设物体与传送带之间的动摩擦因数μ=0.1,A、B间的距离L=2 m,g取10 m/s2.
(1)求物体刚开始运动时所受滑动摩擦力的大小与加速度的大小;
(2)求物体由A运动到B的时间;
(3)如果提高传送带的运行速率,物体就能被较快地传送到B处,求使物体从A处传送到B处的最短时间和传送带对应的最小运行速率.
答案 (1)4 N 1 m/s2 (2)2.5 s (3)2 s 2 m/s
解析 (1)滑动摩擦力Ff1=μmg=0.1×4×10 N=4 N,
加速度a==1 m/s2.
(2)物体匀加速运动的时间t1==1 s,
物体匀加速运动的位移x1==0.5 m.
物体匀速运动的时间t2==1.5 s
则物体由A运动到B的时间t=t1+t2=2.5 s.
(3)物体一直做匀加速运动时物体从A处传送到B处的时间最短,加速度仍为a=1 m/s2,当物体到达B处时,有vmin2=2aL,vmin== m/s=2 m/s,
所以传送带的最小运行速率为2 m/s.
设物体最短运行时间为tmin,则vmin=atmin,
得tmin== s=2 s.
7.如图,一平直的传送带以速率v=2 m/s顺时针匀速运行,在A处把物体轻轻地放到传送带上,经过6 s,物体到达B处,A、B相距L=10 m,重力加速度g=10 m/s2.则:
(1)物体在传送带上匀加速运动的时间是多少?
(2)物体与传送带之间的动摩擦因数为多少?
(3)若物体是煤块,求物体在传送带上的划痕长度.
答案 (1)2 s (2)0.1 (3)2 m
解析 (1)由题意可知,物体从A到B先做匀加速直线运动,后与传送带达到相同速度,匀速运动到B端,
设物体做匀加速运动的时间为t
所以t+v(6 s-t)=L
代入数据解得:t=2 s
(2)在匀加速运动过程中,根据牛顿第二定律可知μmg=ma
根据速度与时间的关系式得:v=at
联立解得:μ=0.1
(3)在物体匀加速运动过程中,传送带上表面相对于地面的位移x=vt=4 m
物体相对于地面的位移x′=at2=2 m
所以物体在传送带上的划痕长度Δx=x-x′=2 m.
训练2 倾斜传送带模型
1.(2022·南京高一期末)传送带被广泛地应用于机场和火车站,如图所示为倾斜传送带装置示意图,传送带足够长,木箱M在静止的传送带上以速度v匀速下滑,某时刻传送带突然顺时针以速度v1启动,则传送带启动后( )
A.木箱M开始加速上滑 B.木箱M开始减速下滑
C.木箱M继续匀速下滑 D.木箱M开始匀速上滑
答案 C
解析 木箱M在静止的传送带上以速度v匀速下滑,受力平衡,说明滑动摩擦力沿传送带向上,大小等于重力沿传送带向下的分力;传送带启动后,木箱相对传送带下滑,受沿传送带向上的滑动摩擦力,大小不变,大小仍然等于重力沿传送带向下的分力,所以木箱继续匀速下滑,故选C.
2.如图所示,足够长的传送带与水平面夹角为θ,以速度v0匀速向下运动,在传送带的上端轻轻放上一个质量为m的小木块,小木块与传送带间的动摩擦因数μ<tan θ,则下列图中能客观地反映小木块的速度随时间变化关系的是( )
答案 D
解析 开始时小木块相对传送带向后运动,滑动摩擦力沿传送带向下,则小木块的加速度为a1=gsin θ+μgcos θ
则第一阶段木块沿传送带向下做匀加速直线运动,因传送带足够长,则木块和传送带能够共速,共速时,因μ<tan θ,木块将继续加速,加速度为a2=gsin θ-μgcos θ,综上所述,木块先以a1做匀加速直线运动,后以a2做匀加速直线运动,故A、B、C错误,D正确.
3.如图,倾角θ=37°、足够长的传送带以恒定速率顺时针运行,现将一质量m=2 kg的小物体轻放在传送带的A端,小物体与传送带间的动摩擦因数μ=0.8,取g=10 m/s2,sin 37°=0.6,cos 37°=0.8,则在上升过程中的小物体( )
A.加速度恒定
B.先加速运动后匀速运动
C.所受的摩擦力方向发生变化
D.所受的摩擦力大小始终为12 N
答案 B
解析 开始时物体受到沿传送带向上的滑动摩擦力,因Ff=μmgcos 37°=12.8 N>mgsin 37°=12 N,则物体沿传送带向上加速运动,由于传送带足够长,当物体的速度与传送带的速度相等时,因μmgcos 37°>mgsin 37°,则之后物体相对传送带静止,随传送带一起匀速向上运动,物体所受静摩擦力大小为12 N,方向沿传送带向上,则选项B正确,A、C、D错误.
4.(2021·泰州中学、南菁高中高一上联考)倾斜传送带以恒定的速率沿逆时针方向运行,如图甲所示.在t=0时,将一小煤块轻放在传送带上A点处,1.5 s时小煤块从B点离开传送带.小煤块速度随时间变化的图像如图乙所示,设沿传送带向下的方向为运动的正方向,取重力加速度g=10 m/s2,不计小煤块与传送带摩擦过程中损失的质量,求:
(1)0~0.5 s内和0.5~1.5 s内小煤块的加速度大小;
(2)小煤块与传送带之间的动摩擦因数;
(3)在0~1.5 s时间内小煤块在传送带上留下的痕迹长度.
答案 见解析
解析 (1)由v-t图像得:0~0.5 s内小煤块的加速度大小a1==10 m/s2
0.5~1.5 s内小煤块的加速度大小
a2==2 m/s2
(2)对小煤块,由牛顿第二定律得:
0~0.5 s内:mgsin θ+μmgcos θ=ma1
0.5~1.5 s内:mgsin θ-μmgcos θ=ma2
联立解得μ=0.5
(3)由v-t图像知,传送带的速度为v1=5 m/s
0~0.5 s内:传送带多运动
Δx1=v1t1-v1t1=1.25 m
0.5~1.5 s内:
小煤块多运动Δx2=(v1+v2)t2-v1t2=1 m
痕迹覆盖,所以0~1.5 s时间内小煤块在传送带上留下的痕迹长度为1.25 m.
5.如图所示,传送带与水平面夹角θ=37°,两轮间距离即A、B两点间长度L=16 m,传送带以v=3 m/s的恒定速率顺时针转动.现有质量m=0.5 kg的物块以初速率v0=1 m/s由底端A处冲上传送带,已知物块与传送带之间的动摩擦因数μ=0.8,重力加速度g取10 m/s2,sin 37°=0.6,cos 37°=0.8.求:
(1)从物块冲上传送带开始计时,经6 s时物块的速度大小.
(2)物块从A运动到B所用的时间.
答案 (1)3 m/s (2)7 s
解析 (1)对物块受力分析如图所示,
由牛顿第二定律得:
μmgcos θ-mgsin θ=ma,
得a=0.4 m/s2
物块运动到与传送带相对静止所用时间
t1==5 s
物块运动的位移x1=t1=t1=10 m
(2)物块匀速运动的位移x2=L-x1=6 m,匀速运动时间t2==2 s
物块从A运动到B所用的时间t=t1+t2=7 s.
6.如图甲所示,倾斜传送带倾角θ=37°,两端A、B间距离为L=4 m,传送带以4 m/s的速度顺时针转动.一质量为1 kg的小滑块从传送带顶端B点由静止释放,沿传送带下滑,到A时用时2 s,g取10 m/s2,sin 37°=0.6,cos 37°=0.8.
(1)求小滑块与传送带间的动摩擦因数;
(2)若该小滑块在传送带的底端A,现用一沿传送带向上的大小为6 N的恒定拉力F拉滑块,使其由静止沿传送带向上运动,当速度与传送带速度相等时,求滑块的位移大小.
(3)在第二问的条件下,求滑块从A运动到B的时间.
答案 见解析
解析 (1)当传送带顺时针转动时,对小滑块由牛顿第二定律可知:mgsin θ-μmgcos θ=ma,
根据位移公式,有L=at2
联立解得:μ=0.5.
(2)传送带的速度为v=4 m/s,当拉力F对滑块作用后,滑块开始做匀加速运动,由牛顿第二定律可得:F+μmgcos θ-mgsin θ=ma1
解得:a1=4 m/s2.
滑块加速到与传送带速度相等的过程,滑块的位移大小为x1== m=2 m,
时间为t1==1 s.
(3)滑块加速到与传送带速度相等之后,
由于F=mgsin θ,
滑块所受摩擦力突变为0,滑块与传送带相对静止,一起匀速运动t2==0.5 s
故tAB=t1+t2=1.5 s.
