2022-2023学年人教版2019物理必修1 第四章 专题强化 实验:验证牛顿第二定律( word版含解析)
文档属性
| 名称 | 2022-2023学年人教版2019物理必修1 第四章 专题强化 实验:验证牛顿第二定律( word版含解析) |  | |
| 格式 | docx | ||
| 文件大小 | 747.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(2019) | ||
| 科目 | 物理 | ||
| 更新时间 | 2022-07-07 16:42:26 | ||
图片预览




文档简介
实验:验证牛顿第二定律
[学习目标] 1.进一步理解探究加速度与力、质量的关系的实验方法.2.会利用牛顿第二定律分析实验数据和实验误差.
在“验证牛顿第二定律”实验中需注意以下几个方面:
1.补偿阻力:适当垫高木板的右端,使小车的重力沿斜面方向的分力正好平衡小车和纸带受到的阻力,在补偿阻力时,不要把悬挂槽码的细绳系在小车上,让小车拉着打点的纸带匀速运动.
2.不重复补偿阻力.
3.实验条件:小车的质量m远大于槽码的质量m′.
4.一先一后一按:改变拉力和小车质量后,每次开始时小车应尽量靠近打点计时器,并应先接通电源,后释放小车,且应在小车到达定滑轮前按住小车.
5.作图像时,要使尽可能多的点在所作直线上,不在直线上的点应尽可能对称分布在所作直线两侧.
6.作图时两坐标轴标度比例要适当.各量需采用国际单位.
例1 某同学用如图所示的实验装置验证牛顿第二定律,请回答下列有关此实验的问题:
(1)该同学在实验前准备了图中所示的实验装置及下列辅助器材:
A.交变电源、导线 B.天平(含配套砝码)
C.秒表 D.刻度尺
E.细线、砂和小砂桶
其中不必要的器材是 (填代号)
(2)打点计时器在小车拖动的纸带上打下一系列点迹,以此记录小车的运动情况,其中一部分纸带上的点迹情况如图甲所示,已知打点计时器打点的时间间隔为0.02 s,测得A点到B、C点的距离分别为x1=5.99 cm、x2=13.59 cm,则在打下点迹B时,小车运动的速度vB= m/s;小车做匀加速直线运动的加速度a= m/s2.(结果均保留三位有效数字)
(3)在验证“质量一定,加速度a与合外力F的关系”时,某学生根据实验数据作出了如图乙所示的a-F图像,其中图线不过原点的原因是 ;图线在末端弯曲的原因是 .
答案 (1)C (2)0.680 1.61 (3)补偿阻力过度 砂和小砂桶的总质量m不远小于小车和砝码的总质量M
解析 (1)由于打点计时器就是一个计时装置,所以不需要秒表.
(2)由题图甲知T=0.1 s,匀变速直线运动的平均速度等于中间时刻的瞬时速度,
vB=≈0.680 m/s,
由Δx=aT2知,(x2-x1)-x1=aT2,
解得a=,
代入数据解得a=1.61 m/s2.
(3)由题图乙知,当F=0时,a≠0,说明重力的分力产生了加速度,所以图线不过原点的原因是补偿阻力过度;以小车、砂和小砂桶整体为研究对象得:mg=(M+m)a,以小车为研究对象得F=Ma,
联立解得F=g=mg,
当M m时F≈mg,
在图线中,F越大,mg越大,就越不满足M m的条件,所以图线在末端弯曲.
例2 (2022·徐州高一期末)某实验小组用图甲所示的装置进行“探究加速度与力、质量的关系”的实验,装置中的力传感器可以把细绳拉力F的大小记录下来.
(1)在实验开始前把木板右侧垫高,以补偿小车在运动时受到的阻力.下列在补偿阻力时做法正确的是 (填选项前的字母).
A.小车前端不挂细绳和槽码
B.小车前端需要挂上细绳和槽码
C.小车尾部不需要安装纸带
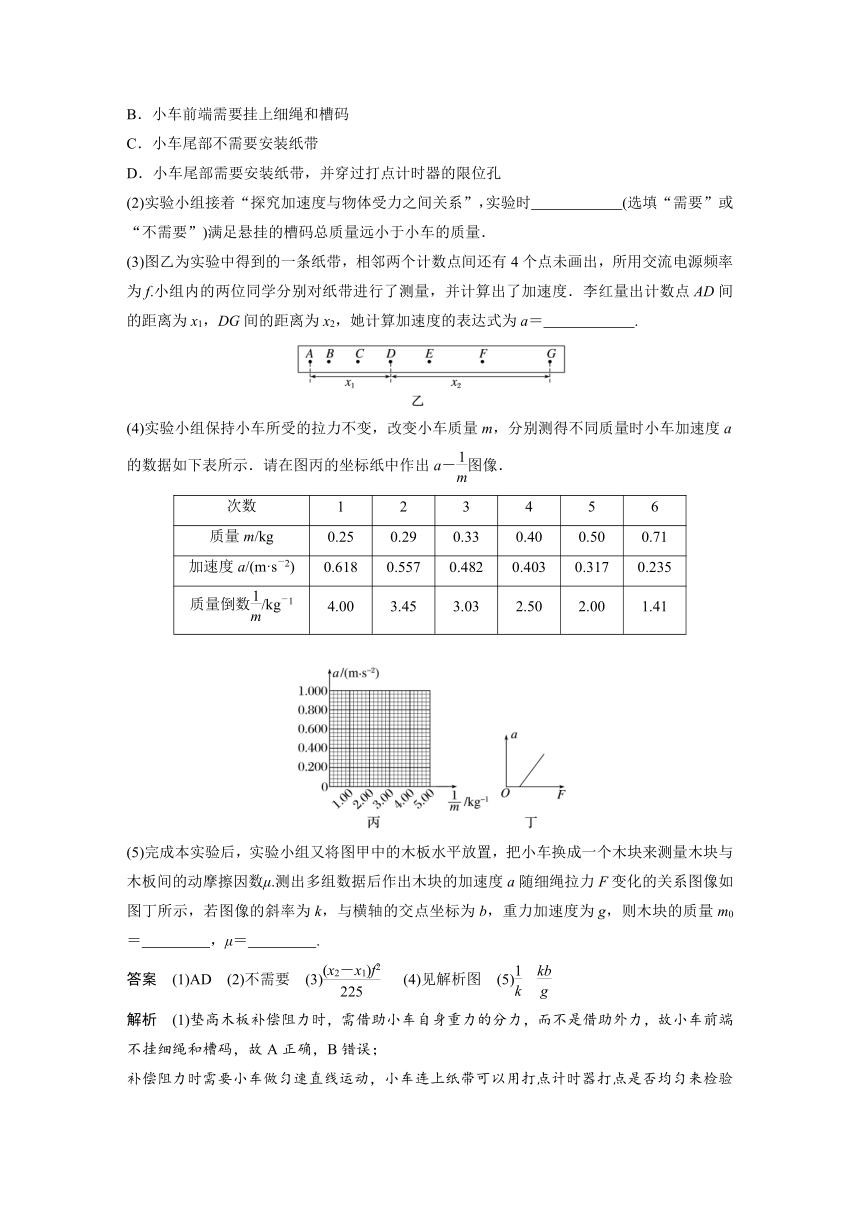
D.小车尾部需要安装纸带,并穿过打点计时器的限位孔
(2)实验小组接着“探究加速度与物体受力之间关系”,实验时 (选填“需要”或“不需要”)满足悬挂的槽码总质量远小于小车的质量.
(3)图乙为实验中得到的一条纸带,相邻两个计数点间还有4个点未画出,所用交流电源频率为f.小组内的两位同学分别对纸带进行了测量,并计算出了加速度.李红量出计数点AD间的距离为x1,DG间的距离为x2,她计算加速度的表达式为a= .
(4)实验小组保持小车所受的拉力不变,改变小车质量m,分别测得不同质量时小车加速度a的数据如下表所示.请在图丙的坐标纸中作出a-图像.
次数 1 2 3 4 5 6
质量m/kg 0.25 0.29 0.33 0.40 0.50 0.71
加速度a/(m·s-2) 0.618 0.557 0.482 0.403 0.317 0.235
质量倒数/kg-1 4.00 3.45 3.03 2.50 2.00 1.41
(5)完成本实验后,实验小组又将图甲中的木板水平放置,把小车换成一个木块来测量木块与木板间的动摩擦因数μ.测出多组数据后作出木块的加速度a随细绳拉力F变化的关系图像如图丁所示,若图像的斜率为k,与横轴的交点坐标为b,重力加速度为g,则木块的质量m0= ,μ= .
答案 (1)AD (2)不需要 (3) (4)见解析图 (5)
解析 (1)垫高木板补偿阻力时,需借助小车自身重力的分力,而不是借助外力,故小车前端不挂细绳和槽码,故A正确,B错误;
补偿阻力时需要小车做匀速直线运动,小车连上纸带可以用打点计时器打点是否均匀来检验是否匀速,同时还能补偿纸带的摩擦力,故小车尾部需要安装纸带,并穿过打点计时器的限位孔,故C错误,D正确.
(2)装置中的力传感器可以测出细绳拉力F的大小,即能测出小车所受的合力,不需要用悬挂的槽码的重力近似代替合力,故不需要满足悬挂的槽码总质量远小于小车的质量.
(3)相邻两个计数点间还有4个点未画出,则计数点的间隔为t=5T=
计数点AD间的距离x1和DG间的距离x2为连续两段位移,由匀变速直线运动的规律可得x2-x1=a(3t)2,
解得a=.
(4)根据表格数据在坐标纸中作出a-图像如图
(5)木块在木板上做匀加速直线运动时,由牛顿第二定律有F-μm0g=m0a
整理可得a=·F-μg
则k=,
可得m0=
a-F图像与横轴的交点坐标为b,即有
0=k·b-μg
解得μ=.
1.在做“探究加速度与力、质量的关系”的实验中,保持小车和砝码的总质量不变,测得小车的加速度a和拉力F的数据如表所示.
F/N 0.20 0.30 0.40 0.50 0.60
a/(m·s-2) 0.11 0.19 0.29 0.40 0.51
(1)根据表中的数据在如图所示的坐标系中作出a-F图像.
(2)图像斜率的物理意义是 .
(3)小车和砝码的总质量为 kg.
(4)图线(或延长线)在F轴上的截距的物理意义是 .
答案 (1)见解析图 (2)小车和砝码总质量的倒数 (3)1 (4)小车受到的阻力为0.1 N
解析 (1)根据所给数据在所给坐标系中准确描点,作出的a-F图像如图所示.
(2)根据a=及(1)中图像可以判断图像斜率表示小车和砝码总质量的倒数.
(3)由==1 kg-1可得M=1 kg.
(4)由a-F图像可知,当力F=0.1 N时,小车开始运动,说明小车受到的阻力为0.1 N.
2.(2022·南京市高一期末)甲、乙两位同学合作完成实验“探究加速度与力、质量的关系”,实验过程中使用如图(a)所示的实验装置,小车及车中砝码总质量为M,托盘和盘中砝码的总质量为m,重力加速度为g,所使用的交流电源频率为50 Hz.
(1)为了使小车所受的拉力近似等于托盘和砝码的总重力,实验时,托盘和盘中砝码的总质量m应满足的条件是 ;
(2)甲同学直接把长木板放在水平桌面上进行实验,完成实验后,用图像法处理数据并且作了小车的a-F图像,如图所示,则甲同学作的图像应该是下图中的 ;
(3)乙同学修正了甲同学实验中存在的问题,并按照正确的步骤完成了实验.如图(b)是乙同学实验中打出的一条纸带,O点是纸带上打出的第一个点,A、B、C、D、E、F、G是计数点,相邻两个计数点间还有4个点未标出,OA间有部分纸带没有画出来,测量出各计数点到O点的距离并标在纸带上,由图中数据可得小车的加速度大小是 m/s2,当打点计时器打D点时,小车的速度大小是 m/s.(以上结果均保留两位有效数字)
(4)为了探究加速度与小车(含车上砝码)的总质量M的关系,两位同学通过正确操作完成六组实验,得到六条纸带,表格中记录的是每组实验中纸带的加速度a以及该组实验中的M、,请在图(c)中作出小车的a-图像.
第一组 第二组 第三组 第四组 第五组 第六组
a/(m·s-2) 2.04 1.63 1.16 0.83 0.51 0.34
M/kg 0.20 0.25 0.35 0.50 0.80 1.20
/kg-1 5.00 4.00 2.86 2.00 1.25 0.83
答案 (1)m M (2)A (3)0.80 0.58 (4)见解析图
解析 (1)若要绳中拉力与托盘和砝码盘的总重力近似相等,需满足m M.
(2)由题图可知,实验时未补偿阻力,绳中拉力大于小车的最大静摩擦力时,小车才能运动.故选A.
(3)由逐差法得a=,vD=
代入数据解得a≈0.80 m/s2,vD≈0.58 m/s
(4)由表中数据可得a-图像如图
3.某实验小组利用图a所示的装置探究加速度与力、质量的关系.
(1)下列做法正确的是 .(填字母代号)
A.调节滑轮的高度,使牵引木块的细绳与长木板保持平行
B.在调节木板倾斜度来补偿木块受到的阻力时,将装有砝码的砝码桶通过定滑轮拴在木块上
C.实验时,先放开木块再接通打点计时器的电源
D.通过增减木块上的砝码改变质量时,不需要重新调节木板倾斜度
(2)为使砝码桶及桶内砝码的总重力在数值上近似等于木块运动时受到的拉力,应满足的条件是砝码桶及桶内砝码的总质量 木块和木块上砝码的总质量.(选填“远大于”“远小于”或“近似等于”)
(3)甲、乙两同学在同一实验室,各取一套图a所示的装置放在水平桌面上,木块上均不放砝码,在没有补偿阻力的情况下,研究加速度a与拉力F的关系,分别得到图b中甲、乙两条直线.设甲、乙两同学用的木块质量分别为m甲、m乙,用的木块与木板间的动摩擦因数分别为μ甲、μ乙,由图可知,m甲 m乙,μ甲 μ乙.(选填“大于”“小于”或“等于”)
答案 (1)AD (2)远小于 (3)小于 大于
解析 (1)实验中细绳要保持与长木板平行,A项正确;补偿阻力时不能将装有砝码的砝码桶通过定滑轮拴在木块上,B项错误;实验时应先接通打点计时器的电源再放开木块,C项错误;通过增减木块上的砝码改变质量时不需要重新补偿阻力,D项正确.
(2)由整体法和隔离法得到细绳中的拉力F=Ma=M=mg,可知,当砝码桶及桶内砝码的总质量m远小于木块和木块上砝码的总质量M时,可得F≈mg.
(3)没有补偿阻力,则F-μmg=ma,a=-μg,a-F图像的斜率大的木块的质量小,纵轴截距绝对值大的动摩擦因数大,因此m甲<m乙,μ甲>μ乙.
4.在“探究加速度与力、质量的关系”的实验中,某同学使用了如图甲所示的装置,木板放在水平桌面上,打点计时器打点频率为50 Hz.
(1)实验中得到如图乙所示的一段纸带,每五个点取一个计数点,测得AB=7.65 cm,BC=
10.17 cm,则实验测出小车的加速度大小为 m/s2.
(2)若直接按题甲所示装置进行实验,以沙和沙桶的总重力产生的拉力F为横轴,通过纸带数据得到的加速度a为纵轴,以下画出的a-F图像合理的是 .
(3)实验中,沙和沙桶的总重力 (填“大于”“小于”或“等于”)绳子对小车的拉力,为了让沙和沙桶的总重力大小更接近绳子对小车的拉力,应让沙和沙桶的总质量 (填“远大于”或“远小于”)小车的质量.
(4)若第(2)问中四个图像中的图线(B、C图线中的直线部分)的斜率为k,则小车的质量M= .
答案 (1)2.52 (2)C (3)大于 远小于 (4)
解析 (1)相邻两计数点间的时间间隔T=0.1 s
小车的加速度大小为
a== m/s2=2.52 m/s2.
(2)若直接按题图甲所示装置进行实验,没有补偿阻力,则当力F达到某一值时小车才有加速度,可知画出的a-F图像合理的是C.
(3)实验中,我们认为绳子对小车的拉力的大小等于沙和沙桶(其总质量为m)的总重力的大小,而实际上绳子的拉力FT=mg-ma,故绳子对小车的拉力小于沙和沙桶的总重力.为了让沙和沙桶的总重力大小更接近绳子对小车的拉力大小,应让沙和沙桶的总质量远小于小车的质量.
(4)由牛顿第二定律得a==·F,
则斜率k=,小车的质量M=.
5.(2021·长治市第二中学高一开学考试)为了探究质量一定时加速度与力的关系,一同学设计了如图所示的实验装置.其中M为带滑轮的小车的质量,m为砂和砂桶的质量.(滑轮质量不计)
(1)实验时,一定要进行的操作是 .
A.用天平测出砂和砂桶的质量
B.将带滑轮的长木板右端垫高,以补偿阻力
C.小车靠近打点计时器,先接通打点计时器的电源,再释放小车,打出一条纸带,同时记录弹簧测力计的示数
D.改变砂和砂桶的质量,打出几条纸带
E.为减小误差,实验中一定要保证砂和砂桶的质量m远小于小车的质量M
(2)该同学在实验中得到如图所示的一条纸带(两计数点间还有两个点没有画出),已知打点计时器采用的是频率为50 Hz的交流电,根据纸带可求出小车的加速度为 m/s2(结果保留两位有效数字).
(3)以弹簧测力计的示数F为横轴,加速度为纵轴,画出的a-F图像是一条直线,如图所示,图线与横轴的夹角为θ,求得图线的斜率为k,则小车的质量为 .
A.2tan θ B. C.k D.
答案 (1)BCD (2)1.3 (3)D
解析 (1)本题拉力可以由弹簧测力计测出,不需要用天平测出砂和砂桶的质量,也就不需要使砂和砂桶的质量远小于车的质量,故A、E错误;该题用弹簧测力计测出拉力,从而表示小车受到的合外力,应将带滑轮的长木板右端垫高,以补偿阻力,故B正确;小车靠近打点计时器,使用打点计时器时,都是先接通电源,待打点稳定后再释放纸带,该实验探究加速度与力的关系,要记录弹簧测力计的示数,故C正确;改变砂和砂桶的质量,即改变拉力的大小,打出几条纸带,研究加速度随F变化的关系,故D正确.
(2)由于两计数点间还有两个点没有画出,相邻计数点之间的时间间隔T=0.06 s,
根据逐差法Δx=aT2
可得小车加速度a=
= m/s2
≈1.3 m/s2
(3)由牛顿第二定律得2F=Ma
解得a=F,
a-F图像的斜率为k=
可得小车质量为M=,
故A、B、C错误,D正确.
[学习目标] 1.进一步理解探究加速度与力、质量的关系的实验方法.2.会利用牛顿第二定律分析实验数据和实验误差.
在“验证牛顿第二定律”实验中需注意以下几个方面:
1.补偿阻力:适当垫高木板的右端,使小车的重力沿斜面方向的分力正好平衡小车和纸带受到的阻力,在补偿阻力时,不要把悬挂槽码的细绳系在小车上,让小车拉着打点的纸带匀速运动.
2.不重复补偿阻力.
3.实验条件:小车的质量m远大于槽码的质量m′.
4.一先一后一按:改变拉力和小车质量后,每次开始时小车应尽量靠近打点计时器,并应先接通电源,后释放小车,且应在小车到达定滑轮前按住小车.
5.作图像时,要使尽可能多的点在所作直线上,不在直线上的点应尽可能对称分布在所作直线两侧.
6.作图时两坐标轴标度比例要适当.各量需采用国际单位.
例1 某同学用如图所示的实验装置验证牛顿第二定律,请回答下列有关此实验的问题:
(1)该同学在实验前准备了图中所示的实验装置及下列辅助器材:
A.交变电源、导线 B.天平(含配套砝码)
C.秒表 D.刻度尺
E.细线、砂和小砂桶
其中不必要的器材是 (填代号)
(2)打点计时器在小车拖动的纸带上打下一系列点迹,以此记录小车的运动情况,其中一部分纸带上的点迹情况如图甲所示,已知打点计时器打点的时间间隔为0.02 s,测得A点到B、C点的距离分别为x1=5.99 cm、x2=13.59 cm,则在打下点迹B时,小车运动的速度vB= m/s;小车做匀加速直线运动的加速度a= m/s2.(结果均保留三位有效数字)
(3)在验证“质量一定,加速度a与合外力F的关系”时,某学生根据实验数据作出了如图乙所示的a-F图像,其中图线不过原点的原因是 ;图线在末端弯曲的原因是 .
答案 (1)C (2)0.680 1.61 (3)补偿阻力过度 砂和小砂桶的总质量m不远小于小车和砝码的总质量M
解析 (1)由于打点计时器就是一个计时装置,所以不需要秒表.
(2)由题图甲知T=0.1 s,匀变速直线运动的平均速度等于中间时刻的瞬时速度,
vB=≈0.680 m/s,
由Δx=aT2知,(x2-x1)-x1=aT2,
解得a=,
代入数据解得a=1.61 m/s2.
(3)由题图乙知,当F=0时,a≠0,说明重力的分力产生了加速度,所以图线不过原点的原因是补偿阻力过度;以小车、砂和小砂桶整体为研究对象得:mg=(M+m)a,以小车为研究对象得F=Ma,
联立解得F=g=mg,
当M m时F≈mg,
在图线中,F越大,mg越大,就越不满足M m的条件,所以图线在末端弯曲.
例2 (2022·徐州高一期末)某实验小组用图甲所示的装置进行“探究加速度与力、质量的关系”的实验,装置中的力传感器可以把细绳拉力F的大小记录下来.
(1)在实验开始前把木板右侧垫高,以补偿小车在运动时受到的阻力.下列在补偿阻力时做法正确的是 (填选项前的字母).
A.小车前端不挂细绳和槽码
B.小车前端需要挂上细绳和槽码
C.小车尾部不需要安装纸带
D.小车尾部需要安装纸带,并穿过打点计时器的限位孔
(2)实验小组接着“探究加速度与物体受力之间关系”,实验时 (选填“需要”或“不需要”)满足悬挂的槽码总质量远小于小车的质量.
(3)图乙为实验中得到的一条纸带,相邻两个计数点间还有4个点未画出,所用交流电源频率为f.小组内的两位同学分别对纸带进行了测量,并计算出了加速度.李红量出计数点AD间的距离为x1,DG间的距离为x2,她计算加速度的表达式为a= .
(4)实验小组保持小车所受的拉力不变,改变小车质量m,分别测得不同质量时小车加速度a的数据如下表所示.请在图丙的坐标纸中作出a-图像.
次数 1 2 3 4 5 6
质量m/kg 0.25 0.29 0.33 0.40 0.50 0.71
加速度a/(m·s-2) 0.618 0.557 0.482 0.403 0.317 0.235
质量倒数/kg-1 4.00 3.45 3.03 2.50 2.00 1.41
(5)完成本实验后,实验小组又将图甲中的木板水平放置,把小车换成一个木块来测量木块与木板间的动摩擦因数μ.测出多组数据后作出木块的加速度a随细绳拉力F变化的关系图像如图丁所示,若图像的斜率为k,与横轴的交点坐标为b,重力加速度为g,则木块的质量m0= ,μ= .
答案 (1)AD (2)不需要 (3) (4)见解析图 (5)
解析 (1)垫高木板补偿阻力时,需借助小车自身重力的分力,而不是借助外力,故小车前端不挂细绳和槽码,故A正确,B错误;
补偿阻力时需要小车做匀速直线运动,小车连上纸带可以用打点计时器打点是否均匀来检验是否匀速,同时还能补偿纸带的摩擦力,故小车尾部需要安装纸带,并穿过打点计时器的限位孔,故C错误,D正确.
(2)装置中的力传感器可以测出细绳拉力F的大小,即能测出小车所受的合力,不需要用悬挂的槽码的重力近似代替合力,故不需要满足悬挂的槽码总质量远小于小车的质量.
(3)相邻两个计数点间还有4个点未画出,则计数点的间隔为t=5T=
计数点AD间的距离x1和DG间的距离x2为连续两段位移,由匀变速直线运动的规律可得x2-x1=a(3t)2,
解得a=.
(4)根据表格数据在坐标纸中作出a-图像如图
(5)木块在木板上做匀加速直线运动时,由牛顿第二定律有F-μm0g=m0a
整理可得a=·F-μg
则k=,
可得m0=
a-F图像与横轴的交点坐标为b,即有
0=k·b-μg
解得μ=.
1.在做“探究加速度与力、质量的关系”的实验中,保持小车和砝码的总质量不变,测得小车的加速度a和拉力F的数据如表所示.
F/N 0.20 0.30 0.40 0.50 0.60
a/(m·s-2) 0.11 0.19 0.29 0.40 0.51
(1)根据表中的数据在如图所示的坐标系中作出a-F图像.
(2)图像斜率的物理意义是 .
(3)小车和砝码的总质量为 kg.
(4)图线(或延长线)在F轴上的截距的物理意义是 .
答案 (1)见解析图 (2)小车和砝码总质量的倒数 (3)1 (4)小车受到的阻力为0.1 N
解析 (1)根据所给数据在所给坐标系中准确描点,作出的a-F图像如图所示.
(2)根据a=及(1)中图像可以判断图像斜率表示小车和砝码总质量的倒数.
(3)由==1 kg-1可得M=1 kg.
(4)由a-F图像可知,当力F=0.1 N时,小车开始运动,说明小车受到的阻力为0.1 N.
2.(2022·南京市高一期末)甲、乙两位同学合作完成实验“探究加速度与力、质量的关系”,实验过程中使用如图(a)所示的实验装置,小车及车中砝码总质量为M,托盘和盘中砝码的总质量为m,重力加速度为g,所使用的交流电源频率为50 Hz.
(1)为了使小车所受的拉力近似等于托盘和砝码的总重力,实验时,托盘和盘中砝码的总质量m应满足的条件是 ;
(2)甲同学直接把长木板放在水平桌面上进行实验,完成实验后,用图像法处理数据并且作了小车的a-F图像,如图所示,则甲同学作的图像应该是下图中的 ;
(3)乙同学修正了甲同学实验中存在的问题,并按照正确的步骤完成了实验.如图(b)是乙同学实验中打出的一条纸带,O点是纸带上打出的第一个点,A、B、C、D、E、F、G是计数点,相邻两个计数点间还有4个点未标出,OA间有部分纸带没有画出来,测量出各计数点到O点的距离并标在纸带上,由图中数据可得小车的加速度大小是 m/s2,当打点计时器打D点时,小车的速度大小是 m/s.(以上结果均保留两位有效数字)
(4)为了探究加速度与小车(含车上砝码)的总质量M的关系,两位同学通过正确操作完成六组实验,得到六条纸带,表格中记录的是每组实验中纸带的加速度a以及该组实验中的M、,请在图(c)中作出小车的a-图像.
第一组 第二组 第三组 第四组 第五组 第六组
a/(m·s-2) 2.04 1.63 1.16 0.83 0.51 0.34
M/kg 0.20 0.25 0.35 0.50 0.80 1.20
/kg-1 5.00 4.00 2.86 2.00 1.25 0.83
答案 (1)m M (2)A (3)0.80 0.58 (4)见解析图
解析 (1)若要绳中拉力与托盘和砝码盘的总重力近似相等,需满足m M.
(2)由题图可知,实验时未补偿阻力,绳中拉力大于小车的最大静摩擦力时,小车才能运动.故选A.
(3)由逐差法得a=,vD=
代入数据解得a≈0.80 m/s2,vD≈0.58 m/s
(4)由表中数据可得a-图像如图
3.某实验小组利用图a所示的装置探究加速度与力、质量的关系.
(1)下列做法正确的是 .(填字母代号)
A.调节滑轮的高度,使牵引木块的细绳与长木板保持平行
B.在调节木板倾斜度来补偿木块受到的阻力时,将装有砝码的砝码桶通过定滑轮拴在木块上
C.实验时,先放开木块再接通打点计时器的电源
D.通过增减木块上的砝码改变质量时,不需要重新调节木板倾斜度
(2)为使砝码桶及桶内砝码的总重力在数值上近似等于木块运动时受到的拉力,应满足的条件是砝码桶及桶内砝码的总质量 木块和木块上砝码的总质量.(选填“远大于”“远小于”或“近似等于”)
(3)甲、乙两同学在同一实验室,各取一套图a所示的装置放在水平桌面上,木块上均不放砝码,在没有补偿阻力的情况下,研究加速度a与拉力F的关系,分别得到图b中甲、乙两条直线.设甲、乙两同学用的木块质量分别为m甲、m乙,用的木块与木板间的动摩擦因数分别为μ甲、μ乙,由图可知,m甲 m乙,μ甲 μ乙.(选填“大于”“小于”或“等于”)
答案 (1)AD (2)远小于 (3)小于 大于
解析 (1)实验中细绳要保持与长木板平行,A项正确;补偿阻力时不能将装有砝码的砝码桶通过定滑轮拴在木块上,B项错误;实验时应先接通打点计时器的电源再放开木块,C项错误;通过增减木块上的砝码改变质量时不需要重新补偿阻力,D项正确.
(2)由整体法和隔离法得到细绳中的拉力F=Ma=M=mg,可知,当砝码桶及桶内砝码的总质量m远小于木块和木块上砝码的总质量M时,可得F≈mg.
(3)没有补偿阻力,则F-μmg=ma,a=-μg,a-F图像的斜率大的木块的质量小,纵轴截距绝对值大的动摩擦因数大,因此m甲<m乙,μ甲>μ乙.
4.在“探究加速度与力、质量的关系”的实验中,某同学使用了如图甲所示的装置,木板放在水平桌面上,打点计时器打点频率为50 Hz.
(1)实验中得到如图乙所示的一段纸带,每五个点取一个计数点,测得AB=7.65 cm,BC=
10.17 cm,则实验测出小车的加速度大小为 m/s2.
(2)若直接按题甲所示装置进行实验,以沙和沙桶的总重力产生的拉力F为横轴,通过纸带数据得到的加速度a为纵轴,以下画出的a-F图像合理的是 .
(3)实验中,沙和沙桶的总重力 (填“大于”“小于”或“等于”)绳子对小车的拉力,为了让沙和沙桶的总重力大小更接近绳子对小车的拉力,应让沙和沙桶的总质量 (填“远大于”或“远小于”)小车的质量.
(4)若第(2)问中四个图像中的图线(B、C图线中的直线部分)的斜率为k,则小车的质量M= .
答案 (1)2.52 (2)C (3)大于 远小于 (4)
解析 (1)相邻两计数点间的时间间隔T=0.1 s
小车的加速度大小为
a== m/s2=2.52 m/s2.
(2)若直接按题图甲所示装置进行实验,没有补偿阻力,则当力F达到某一值时小车才有加速度,可知画出的a-F图像合理的是C.
(3)实验中,我们认为绳子对小车的拉力的大小等于沙和沙桶(其总质量为m)的总重力的大小,而实际上绳子的拉力FT=mg-ma,故绳子对小车的拉力小于沙和沙桶的总重力.为了让沙和沙桶的总重力大小更接近绳子对小车的拉力大小,应让沙和沙桶的总质量远小于小车的质量.
(4)由牛顿第二定律得a==·F,
则斜率k=,小车的质量M=.
5.(2021·长治市第二中学高一开学考试)为了探究质量一定时加速度与力的关系,一同学设计了如图所示的实验装置.其中M为带滑轮的小车的质量,m为砂和砂桶的质量.(滑轮质量不计)
(1)实验时,一定要进行的操作是 .
A.用天平测出砂和砂桶的质量
B.将带滑轮的长木板右端垫高,以补偿阻力
C.小车靠近打点计时器,先接通打点计时器的电源,再释放小车,打出一条纸带,同时记录弹簧测力计的示数
D.改变砂和砂桶的质量,打出几条纸带
E.为减小误差,实验中一定要保证砂和砂桶的质量m远小于小车的质量M
(2)该同学在实验中得到如图所示的一条纸带(两计数点间还有两个点没有画出),已知打点计时器采用的是频率为50 Hz的交流电,根据纸带可求出小车的加速度为 m/s2(结果保留两位有效数字).
(3)以弹簧测力计的示数F为横轴,加速度为纵轴,画出的a-F图像是一条直线,如图所示,图线与横轴的夹角为θ,求得图线的斜率为k,则小车的质量为 .
A.2tan θ B. C.k D.
答案 (1)BCD (2)1.3 (3)D
解析 (1)本题拉力可以由弹簧测力计测出,不需要用天平测出砂和砂桶的质量,也就不需要使砂和砂桶的质量远小于车的质量,故A、E错误;该题用弹簧测力计测出拉力,从而表示小车受到的合外力,应将带滑轮的长木板右端垫高,以补偿阻力,故B正确;小车靠近打点计时器,使用打点计时器时,都是先接通电源,待打点稳定后再释放纸带,该实验探究加速度与力的关系,要记录弹簧测力计的示数,故C正确;改变砂和砂桶的质量,即改变拉力的大小,打出几条纸带,研究加速度随F变化的关系,故D正确.
(2)由于两计数点间还有两个点没有画出,相邻计数点之间的时间间隔T=0.06 s,
根据逐差法Δx=aT2
可得小车加速度a=
= m/s2
≈1.3 m/s2
(3)由牛顿第二定律得2F=Ma
解得a=F,
a-F图像的斜率为k=
可得小车质量为M=,
故A、B、C错误,D正确.
