苏科版七年级上册数学 4.3.6用柱状示意图解决问题 教案(表格式)
文档属性
| 名称 | 苏科版七年级上册数学 4.3.6用柱状示意图解决问题 教案(表格式) |

|
|
| 格式 | doc | ||
| 文件大小 | 64.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-07-07 00:00:00 | ||
图片预览

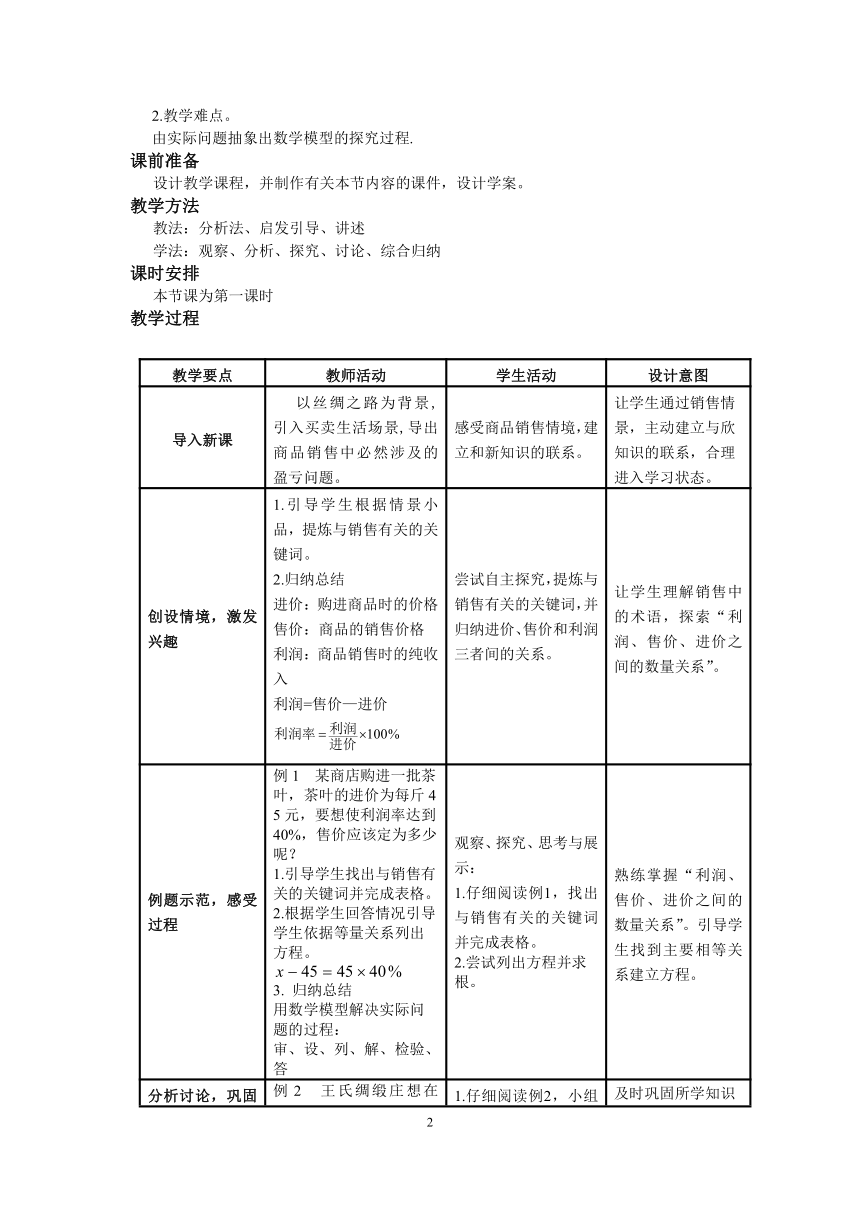
文档简介
第四章 一元一次方程
用柱状示意图解决问题
教材分析
本节内容是在前面两节已经讨论过由实际问题建立一元一次方程和解一元一次方程的一般步骤的基础上,进一步以探究的形式讨论如何用一元一次方程解决实际问题。本节选择了具有一定综合性的问题(销售中的盈亏),设置了探究点,引导学生利用方程为工具进行具有一定深度的思考,具有承上启下的作用,把全章所强调的以方程为工具把实际问题模型化的思想提到新的高度。安排这节的目的在于:一方面通过更加贴近实际生活的问题,进一步突出方程这种数学模型的应用具有广泛性和有效性;另一方面使学生能在更加贴近实际生活的问题情境中运用所学数学知识,激发学生学习数学的兴趣,使学生在分析问题和解决问题能力、创新精神和实践意识在更高层次上得到提高。为以后几节列方程解生活中的实际问题的应用埋下伏笔。更为我们以后类比学习用二元一次方程、二元一次方程组、一元二次方程解决实际问题打好基础,既是前面所学知识的延伸,又是后面要学习的内容的重要预备知识。因此,这一节课无论在知识上,还是对学生能力的培养上,都有着十分重要的作用。
学情分析
在日常生活中,学生对进价、售价、利润、利润率、盈亏等这些知识积累了一定的生活经验,但对这些量之间存在的数量关系认识得不够清楚,解决问题的逻辑思维不够清晰。本节内容是生活中的常见现象,学生可以利用现有知识和生活经验,在教师的适当点拔、引导下,得出盈亏问题中的数量关系,刻画模型,解决问题。另外,七年级学生天真活泼、对新生事物很感兴趣、具有强烈的好奇心,为此我精心设计好教学环节,搭建平台,突出重点,突破难点,体验数学模型的探究过程。
教学目标
结合本节课的具体内容和学生的实际情况,我确定本节课的教学目标为:
1.知识与技能
(1)通过活动一让学生理解销售中的术语,探索“利润、售价、进价之间的数量关系”。
(2)熟练掌握“利润、售价、进价之间的数量关系”。知道三个量中知二推一。
(3)根据利润、进价、售价之间的数量关系建立一元一次方程的数学模型并解决销售中的盈亏问题.
2.过程与方法
(1)通过活动二,让学生体会用方程去解决实际问题的思想,提高分析问题、解决问题的能力;
(2)利用探究题激发学生的学习潜能,促使他们在自主探索与合作交流的过程中真正理解和掌握基本数学知识、技能、数学思想方法,获得广泛的数学行动经验,提高解决问题的能力,学会学习.
3.情感、态度与价值观
(1)通过对打折销售问题的探索, 让学生体验生活中数学的应用与价值,感受数学来源于生活,感受数学与人类生活的密切联系,激发学生学数学,用数学的兴趣;
(2)培养学生勤于思考、乐于探究、敢于发表自己观点的学习习惯,从实际问题中体验数学的价值.
教学重点和难点
1.教学重点。
通过解决销售中的盈亏问题,体验建立方程模型解决问题的一般过程.
2.教学难点。
由实际问题抽象出数学模型的探究过程.
课前准备
设计教学课程,并制作有关本节内容的课件,设计学案。
教学方法
教法:分析法、启发引导、讲述
学法:观察、分析、探究、讨论、综合归纳
课时安排
本节课为第一课时
教学过程
教学要点 教师活动 学生活动 设计意图
导入新课 以丝绸之路为背景,引入买卖生活场景,导出商品销售中必然涉及的盈亏问题。 感受商品销售情境,建立和新知识的联系。 让学生通过销售情景,主动建立与欣知识的联系,合理进入学习状态。
创设情境,激发兴趣 1.引导学生根据情景小品,提炼与销售有关的关键词。2.归纳总结进价:购进商品时的价格售价:商品的销售价格利润:商品销售时的纯收入利润=售价—进价 尝试自主探究,提炼与销售有关的关键词,并归纳进价、售价和利润三者间的关系。 让学生理解销售中的术语,探索“利润、售价、进价之间的数量关系”。
例题示范,感受过程 例1 某商店购进一批茶叶,茶叶的进价为每斤45元,要想使利润率达到40%,售价应该定为多少呢?1.引导学生找出与销售有关的关键词并完成表格。2.根据学生回答情况引导学生依据等量关系列出方程。3. 归纳总结用数学模型解决实际问题的过程:审、设、列、解、检验、答 观察、探究、思考与展示:1.仔细阅读例1,找出与销售有关的关键词并完成表格。2.尝试列出方程并求根。 熟练掌握“利润、售价、进价之间的数量关系”。引导学生找到主要相等关系建立方程。
分析讨论,巩固应用 例2 王氏绸缎庄想在“元旦节”搞优惠活动.老板先把每匹绸缎的售价提高75元标价,再在牌子上写“大酬宾,八折优惠”,结果每匹绸缎获利40元,若每匹绸缎的进价为140元,则每匹绸缎打折后确实便宜了吗?1.引导学生并完成柱状图。2.根据柱状图引导学生依据等量关系列出方程。3.引导学生回答问题“每匹绸缎打折后确实便宜了吗?”。4.对折扣(8折)进行深入讲解,让学生理解四个量的关系及应用。 1.仔细阅读例2,小组讨论,找到题目中的关键词,并完成柱状图。2.尝试列出方程并求根。3.巩固提升,根据方程的根完成实际问题。 及时巩固所学知识通过创设真实情景,让学生进一步感受把实际问题抽象成数学问题的过程,从而培养学生分析问题和解决问题的能力.
合作交流,探究方法 例3已知A、B两件服装的成本共500元,服装店老板分别以30%和20%的利润定价后进行销售,该服装店共获利130元.(1) A、B两件服装的成本各是多少元?(2)若A服装的定价为500,则这件服装可打几折销售?1.老师请学生板演,然后请其他同学对黑板上的内容发表自己的观点,老师点评。 1.学生独立思考,完成问题。2.对黑板上其他同学的过程和结论发表自己的观点。 讨论、交流,使学生学会合作并能与他人交流思维的过程和结果,同时在参与中独立思考。对数学问题的讨论,敢于发表自己的观点,并尊重与理解他人的见解,能从交流中获益.
联想探究,拓展思维 组织学生根据方程,变出符合方程的实际问题。 畅所欲言 渗透数学建模思想,培养运用一元一次方程分析和解决实际问题的能力。
归纳总结,反思提高 整合知识点:1本节课你知道了那些与销售有关的量? 2你是如何梳理题目中的有关量并找到等量关系的? 在教师的引导下整合知识点 小结用一元一次方程解决实际问题的一般步骤,提高归纳概括能力和语言表达能力.明确数学思想方法。
推荐作业,巩固提高 必做题:分别以7,28,50%或者300,15,50%编一道关于打折销售的应用题.选做题:请同学们在生活中再收集一些有关打折销售的的问题,用一元一次方程解决实际问题. 巩固提高
板书设计:
课后反思:
一元一次方程
——销售中的盈亏
利润=售价—进价 例2
例3
2
用柱状示意图解决问题
教材分析
本节内容是在前面两节已经讨论过由实际问题建立一元一次方程和解一元一次方程的一般步骤的基础上,进一步以探究的形式讨论如何用一元一次方程解决实际问题。本节选择了具有一定综合性的问题(销售中的盈亏),设置了探究点,引导学生利用方程为工具进行具有一定深度的思考,具有承上启下的作用,把全章所强调的以方程为工具把实际问题模型化的思想提到新的高度。安排这节的目的在于:一方面通过更加贴近实际生活的问题,进一步突出方程这种数学模型的应用具有广泛性和有效性;另一方面使学生能在更加贴近实际生活的问题情境中运用所学数学知识,激发学生学习数学的兴趣,使学生在分析问题和解决问题能力、创新精神和实践意识在更高层次上得到提高。为以后几节列方程解生活中的实际问题的应用埋下伏笔。更为我们以后类比学习用二元一次方程、二元一次方程组、一元二次方程解决实际问题打好基础,既是前面所学知识的延伸,又是后面要学习的内容的重要预备知识。因此,这一节课无论在知识上,还是对学生能力的培养上,都有着十分重要的作用。
学情分析
在日常生活中,学生对进价、售价、利润、利润率、盈亏等这些知识积累了一定的生活经验,但对这些量之间存在的数量关系认识得不够清楚,解决问题的逻辑思维不够清晰。本节内容是生活中的常见现象,学生可以利用现有知识和生活经验,在教师的适当点拔、引导下,得出盈亏问题中的数量关系,刻画模型,解决问题。另外,七年级学生天真活泼、对新生事物很感兴趣、具有强烈的好奇心,为此我精心设计好教学环节,搭建平台,突出重点,突破难点,体验数学模型的探究过程。
教学目标
结合本节课的具体内容和学生的实际情况,我确定本节课的教学目标为:
1.知识与技能
(1)通过活动一让学生理解销售中的术语,探索“利润、售价、进价之间的数量关系”。
(2)熟练掌握“利润、售价、进价之间的数量关系”。知道三个量中知二推一。
(3)根据利润、进价、售价之间的数量关系建立一元一次方程的数学模型并解决销售中的盈亏问题.
2.过程与方法
(1)通过活动二,让学生体会用方程去解决实际问题的思想,提高分析问题、解决问题的能力;
(2)利用探究题激发学生的学习潜能,促使他们在自主探索与合作交流的过程中真正理解和掌握基本数学知识、技能、数学思想方法,获得广泛的数学行动经验,提高解决问题的能力,学会学习.
3.情感、态度与价值观
(1)通过对打折销售问题的探索, 让学生体验生活中数学的应用与价值,感受数学来源于生活,感受数学与人类生活的密切联系,激发学生学数学,用数学的兴趣;
(2)培养学生勤于思考、乐于探究、敢于发表自己观点的学习习惯,从实际问题中体验数学的价值.
教学重点和难点
1.教学重点。
通过解决销售中的盈亏问题,体验建立方程模型解决问题的一般过程.
2.教学难点。
由实际问题抽象出数学模型的探究过程.
课前准备
设计教学课程,并制作有关本节内容的课件,设计学案。
教学方法
教法:分析法、启发引导、讲述
学法:观察、分析、探究、讨论、综合归纳
课时安排
本节课为第一课时
教学过程
教学要点 教师活动 学生活动 设计意图
导入新课 以丝绸之路为背景,引入买卖生活场景,导出商品销售中必然涉及的盈亏问题。 感受商品销售情境,建立和新知识的联系。 让学生通过销售情景,主动建立与欣知识的联系,合理进入学习状态。
创设情境,激发兴趣 1.引导学生根据情景小品,提炼与销售有关的关键词。2.归纳总结进价:购进商品时的价格售价:商品的销售价格利润:商品销售时的纯收入利润=售价—进价 尝试自主探究,提炼与销售有关的关键词,并归纳进价、售价和利润三者间的关系。 让学生理解销售中的术语,探索“利润、售价、进价之间的数量关系”。
例题示范,感受过程 例1 某商店购进一批茶叶,茶叶的进价为每斤45元,要想使利润率达到40%,售价应该定为多少呢?1.引导学生找出与销售有关的关键词并完成表格。2.根据学生回答情况引导学生依据等量关系列出方程。3. 归纳总结用数学模型解决实际问题的过程:审、设、列、解、检验、答 观察、探究、思考与展示:1.仔细阅读例1,找出与销售有关的关键词并完成表格。2.尝试列出方程并求根。 熟练掌握“利润、售价、进价之间的数量关系”。引导学生找到主要相等关系建立方程。
分析讨论,巩固应用 例2 王氏绸缎庄想在“元旦节”搞优惠活动.老板先把每匹绸缎的售价提高75元标价,再在牌子上写“大酬宾,八折优惠”,结果每匹绸缎获利40元,若每匹绸缎的进价为140元,则每匹绸缎打折后确实便宜了吗?1.引导学生并完成柱状图。2.根据柱状图引导学生依据等量关系列出方程。3.引导学生回答问题“每匹绸缎打折后确实便宜了吗?”。4.对折扣(8折)进行深入讲解,让学生理解四个量的关系及应用。 1.仔细阅读例2,小组讨论,找到题目中的关键词,并完成柱状图。2.尝试列出方程并求根。3.巩固提升,根据方程的根完成实际问题。 及时巩固所学知识通过创设真实情景,让学生进一步感受把实际问题抽象成数学问题的过程,从而培养学生分析问题和解决问题的能力.
合作交流,探究方法 例3已知A、B两件服装的成本共500元,服装店老板分别以30%和20%的利润定价后进行销售,该服装店共获利130元.(1) A、B两件服装的成本各是多少元?(2)若A服装的定价为500,则这件服装可打几折销售?1.老师请学生板演,然后请其他同学对黑板上的内容发表自己的观点,老师点评。 1.学生独立思考,完成问题。2.对黑板上其他同学的过程和结论发表自己的观点。 讨论、交流,使学生学会合作并能与他人交流思维的过程和结果,同时在参与中独立思考。对数学问题的讨论,敢于发表自己的观点,并尊重与理解他人的见解,能从交流中获益.
联想探究,拓展思维 组织学生根据方程,变出符合方程的实际问题。 畅所欲言 渗透数学建模思想,培养运用一元一次方程分析和解决实际问题的能力。
归纳总结,反思提高 整合知识点:1本节课你知道了那些与销售有关的量? 2你是如何梳理题目中的有关量并找到等量关系的? 在教师的引导下整合知识点 小结用一元一次方程解决实际问题的一般步骤,提高归纳概括能力和语言表达能力.明确数学思想方法。
推荐作业,巩固提高 必做题:分别以7,28,50%或者300,15,50%编一道关于打折销售的应用题.选做题:请同学们在生活中再收集一些有关打折销售的的问题,用一元一次方程解决实际问题. 巩固提高
板书设计:
课后反思:
一元一次方程
——销售中的盈亏
利润=售价—进价 例2
例3
2
同课章节目录
- 第1章 我们与数学同行
- 1.1 生活 数学
- 1.2 活动 思考
- 第2章 有理数
- 2.1 正数与负数
- 2.2 有理数与无理数
- 2.3 数轴
- 2.4 绝对值与相反数
- 2.5 有理数的加法与减法
- 2.6 有理数的乘法与除法
- 2.7 有理数的乘方
- 2.8 有理数的混合运算
- 第3章 代数式
- 3.1 字母表示数
- 3.2 代数式
- 3.3 代数式的值
- 3.4 合并同类项
- 3.5 去括号
- 3.6 整式的加减
- 第4章 一元一次方程
- 4.1 从问题到方程
- 4.2 解一元一次方程
- 4.3 用一元一次方程解决问题
- 第5章 走进图形世界
- 5.1 丰富的图形世界
- 5.2 图形的运动
- 5.3 展开与折叠
- 5.4 主视图、左视图、俯视图
- 第6章 平面图形的认识(一)
- 6.1 线段 射线 直线
- 6.2 角
- 6.3 余角 补角 对顶角
- 6.4 平行
- 6.5 垂直
