青岛版五四制四年级数学下册因数与倍数总复习课件
文档属性
| 名称 | 青岛版五四制四年级数学下册因数与倍数总复习课件 |  | |
| 格式 | zip | ||
| 文件大小 | 815.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 青岛版(五四制) | ||
| 科目 | 数学 | ||
| 更新时间 | 2013-06-26 17:49:33 | ||
图片预览








文档简介
课件29张PPT。因数和倍数
整理和复习3×6=183和6是18的因数,18是3的倍数,也是6的倍数。a×b=c (a,b,c都是不为0的自然数)a和b是c的因数,
c是a的倍数,也是b的倍数。在4、9 和 24 中,
( )是( )的倍数,
( )是( )的因数,
( )和( )只有公因数1。2494244418÷6=3( )和( ) 是( )的因数,( )是( )的倍数3×6=18( )×( )= 36(2 )×(18 )= 36(3 )×(12 )= 36 (4 )×(9 )= 36(6 )×(6 )= 3613636的因数有:
1,2,3,4,6,9,12,18,36。36的倍数有:72,108,···36,一个数的最小倍数和最大因数相等36的因数有:1,2,3,4,6,9,12,18,36。3636 一个数,既是28的倍数,又是28的因数,这个数是( )。28两个数的( )的个数是无限的。
A 最大公因数 B 公因数
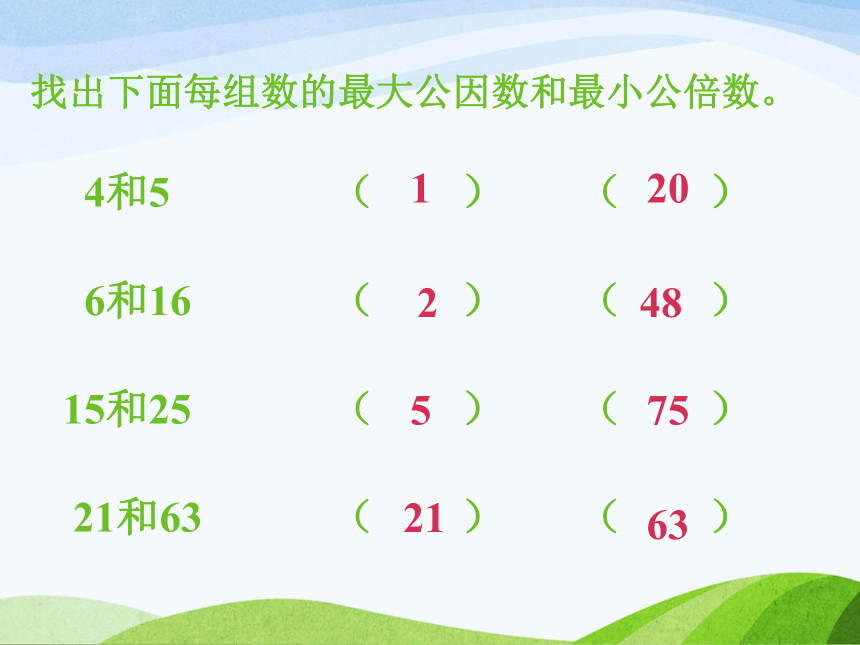
C 公倍数 D 最小公倍数C找出下面每组数的最大公因数和最小公倍数。
4和5 ( ) ( )
6和16 ( ) ( )
15和25 ( ) ( )
21和63 ( ) ( )1632175524820a和b是非零自然数,
若 a÷b = 5, 则a和b的最大公因数是
( ), 最小公倍数是( );baa = 5ba和b是非零自然数,
若a和b的公因数只有1, 则a和b的最大公因数是( ), 最小公倍数是( )。1ab在 1,2,15,48,60,13,39 中,
(1)质数有:
(2)合数有:
(3) 奇数有:
(4)偶数有:15,48,60 ,391, 15,13, 392,48,602,13在1,2,15,48,60,13,39中,
(1)2的倍数有:
(2) 3的倍数有:
(3) 5的倍数有:
(4)是2的倍数又是5的倍数有:
(5)有因数2,3,5 的有:2,48,6015,48,60, 3915,606060填 一填(1) 最小的自然数是( )。(2) 最小的质数是( ) , 最小的合数是( )。24(3)10以内的最大奇数是( )。9(4)5的最小倍数是( )。 50判断并说出理由。
1.所有的质数都是奇数。 ( )
2.所有的奇数都是质数。 ( )
3.所有的合数都是偶数。 ( )
4.所有的偶数都是合数。 ( )
5.自然数中除了奇数就是偶数。( )
××××√ 6. 自然数中除了质数就是合数。( )
7. 12是倍数,3是因数。 ( )
8. 1是奇数而不是质数。 ( )
9. 2是偶数也是质数。 ( )××√√要使这个数能被 3 整除,□里可以填 1 2 □0369 0、3、6、9
2.要使这个数能被 5 整除,□里可以填 1 2 □050、53.要使这个数能被 2、3整除,□里可以填 1 2 □060、64.要使这个数能被 2、5整除,□里可以填 1 2 □05.要使这个数能被 3、5整除,□里可以填 1 2 □06.要使这个数能被 2、3、5整除,□里可以填 1 2 □0填空:
1-20各数中,最大的质数是( ),最小的合数是( )。填素数:21=( )+( )=( )× ( )=( )-( )20以内,最小的素数与最大的合数的和是( ),
积是( )。
一个三位数,既是2的倍数又是3的倍数,又有因数5,这样
的数最小是( ),最大是( )。一个五位数,最高位是最小的奇数,百位上是最小的合数,
个位是最小的素数,其他位是0,这个数是( )。1941923723 22240120 99010402 判断:
1、一个数的倍数一定比它的因数大。( )
2、2的倍数一定是合数。( )
3、所有奇数都是质数。( )
4、所有偶数都是合数。( )
5、质数只能被1和它本身整除。( )
6、一个合数,肯定有3个或3个以上的因数。( )
7、是奇数又是合数且最小的是15。( )
(1)一个数的倍数都比它的因数大。 ( ) (2)4.2÷0.6=7,我们说4.2是0.6的倍数。 ( ) (3)24÷6=4,我们说24是倍数,6是因数。 ( ) (4)是互质数的两个数一定是质数。 ( ) (5)两个质数相乘的积一定是合数。 ( ) (6)如果一个自然数是6的倍数,那么它一定是2的倍数。
( )猜年龄:
提示1:我的年龄数是个奇数;
提示2:我的年龄数减去1就是5的倍数。
提示3:我的年龄数只有两个因数。电话号码可能是多少?A: 2的倍数; B:最小的自然数;C: 10 以内最大的奇数;D: 它的质因数是 3 个 2 ;E: 加上 1 就是最小的合数; F: 2 和 3 的最小公倍数;G: 最大的因数是 5 。2098365 2、4、6、8 0 9 8 3 6 5猜电话号码:
第一位数字既不是质数也不是合数;
第二位数字是所有自然数的因数;
第三位数字是3的倍数而且是10以内最大的倍数。数学日记
日期:_____ 姓名:_______
今天的数学课的课题: ____________
所涉及的重要数学概念: _____________
理解的最好的地方: __________________
不明白或还需要进步理解的地方: ________
所学的内容能否应用在日常生活中,举例说明: _______
整理和复习3×6=183和6是18的因数,18是3的倍数,也是6的倍数。a×b=c (a,b,c都是不为0的自然数)a和b是c的因数,
c是a的倍数,也是b的倍数。在4、9 和 24 中,
( )是( )的倍数,
( )是( )的因数,
( )和( )只有公因数1。2494244418÷6=3( )和( ) 是( )的因数,( )是( )的倍数3×6=18( )×( )= 36(2 )×(18 )= 36(3 )×(12 )= 36 (4 )×(9 )= 36(6 )×(6 )= 3613636的因数有:
1,2,3,4,6,9,12,18,36。36的倍数有:72,108,···36,一个数的最小倍数和最大因数相等36的因数有:1,2,3,4,6,9,12,18,36。3636 一个数,既是28的倍数,又是28的因数,这个数是( )。28两个数的( )的个数是无限的。
A 最大公因数 B 公因数
C 公倍数 D 最小公倍数C找出下面每组数的最大公因数和最小公倍数。
4和5 ( ) ( )
6和16 ( ) ( )
15和25 ( ) ( )
21和63 ( ) ( )1632175524820a和b是非零自然数,
若 a÷b = 5, 则a和b的最大公因数是
( ), 最小公倍数是( );baa = 5ba和b是非零自然数,
若a和b的公因数只有1, 则a和b的最大公因数是( ), 最小公倍数是( )。1ab在 1,2,15,48,60,13,39 中,
(1)质数有:
(2)合数有:
(3) 奇数有:
(4)偶数有:15,48,60 ,391, 15,13, 392,48,602,13在1,2,15,48,60,13,39中,
(1)2的倍数有:
(2) 3的倍数有:
(3) 5的倍数有:
(4)是2的倍数又是5的倍数有:
(5)有因数2,3,5 的有:2,48,6015,48,60, 3915,606060填 一填(1) 最小的自然数是( )。(2) 最小的质数是( ) , 最小的合数是( )。24(3)10以内的最大奇数是( )。9(4)5的最小倍数是( )。 50判断并说出理由。
1.所有的质数都是奇数。 ( )
2.所有的奇数都是质数。 ( )
3.所有的合数都是偶数。 ( )
4.所有的偶数都是合数。 ( )
5.自然数中除了奇数就是偶数。( )
××××√ 6. 自然数中除了质数就是合数。( )
7. 12是倍数,3是因数。 ( )
8. 1是奇数而不是质数。 ( )
9. 2是偶数也是质数。 ( )××√√要使这个数能被 3 整除,□里可以填 1 2 □0369 0、3、6、9
2.要使这个数能被 5 整除,□里可以填 1 2 □050、53.要使这个数能被 2、3整除,□里可以填 1 2 □060、64.要使这个数能被 2、5整除,□里可以填 1 2 □05.要使这个数能被 3、5整除,□里可以填 1 2 □06.要使这个数能被 2、3、5整除,□里可以填 1 2 □0填空:
1-20各数中,最大的质数是( ),最小的合数是( )。填素数:21=( )+( )=( )× ( )=( )-( )20以内,最小的素数与最大的合数的和是( ),
积是( )。
一个三位数,既是2的倍数又是3的倍数,又有因数5,这样
的数最小是( ),最大是( )。一个五位数,最高位是最小的奇数,百位上是最小的合数,
个位是最小的素数,其他位是0,这个数是( )。1941923723 22240120 99010402 判断:
1、一个数的倍数一定比它的因数大。( )
2、2的倍数一定是合数。( )
3、所有奇数都是质数。( )
4、所有偶数都是合数。( )
5、质数只能被1和它本身整除。( )
6、一个合数,肯定有3个或3个以上的因数。( )
7、是奇数又是合数且最小的是15。( )
(1)一个数的倍数都比它的因数大。 ( ) (2)4.2÷0.6=7,我们说4.2是0.6的倍数。 ( ) (3)24÷6=4,我们说24是倍数,6是因数。 ( ) (4)是互质数的两个数一定是质数。 ( ) (5)两个质数相乘的积一定是合数。 ( ) (6)如果一个自然数是6的倍数,那么它一定是2的倍数。
( )猜年龄:
提示1:我的年龄数是个奇数;
提示2:我的年龄数减去1就是5的倍数。
提示3:我的年龄数只有两个因数。电话号码可能是多少?A: 2的倍数; B:最小的自然数;C: 10 以内最大的奇数;D: 它的质因数是 3 个 2 ;E: 加上 1 就是最小的合数; F: 2 和 3 的最小公倍数;G: 最大的因数是 5 。2098365 2、4、6、8 0 9 8 3 6 5猜电话号码:
第一位数字既不是质数也不是合数;
第二位数字是所有自然数的因数;
第三位数字是3的倍数而且是10以内最大的倍数。数学日记
日期:_____ 姓名:_______
今天的数学课的课题: ____________
所涉及的重要数学概念: _____________
理解的最好的地方: __________________
不明白或还需要进步理解的地方: ________
所学的内容能否应用在日常生活中,举例说明: _______
