人教版九年级下册 反比例函数的图象和性质的应用(第2课时 ) 课件(共25张PPT)
文档属性
| 名称 | 人教版九年级下册 反比例函数的图象和性质的应用(第2课时 ) 课件(共25张PPT) |

|
|
| 格式 | ppt | ||
| 文件大小 | 819.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-07-08 05:59:57 | ||
图片预览




文档简介
(共25张PPT)
第26章 反比例函数
26.1 反比例函数
26.1.2 反比例函数的图象和性质
第2课时 反比例函数的图象和性质的应用
温故引新
问题1:反比例函数的解析式有哪几种 反比例函数有哪些性质
2.当k>0时,在每个象限内y随x的增大而减小;
当k<0时,在每个象限内y随x的增大而增大.
反比例函数解析式有三种:
解:
反比例函数的性质有:
1.它的图象是关于原点中心对称的双曲线.
问题2:已知点(2,-6)在反比例函数的图象上,点(-2,6) 是否也在此图象上?点(-6,2)和(6,-2)呢?
解:点(-2,6), (-6,2)和(6,-2)都
在这个反比例函数图像上.
温故引新
温故引新
阅读教材第7页例3,思考:
(1)确定一个反比例函数的解析式需要什么条件?
已知函数图象上的一个点的坐标即可
(2)如何判断一个点是否在反比例函数的图象上?
看该点的坐标是否满足反比例函数的解析式
例题评析
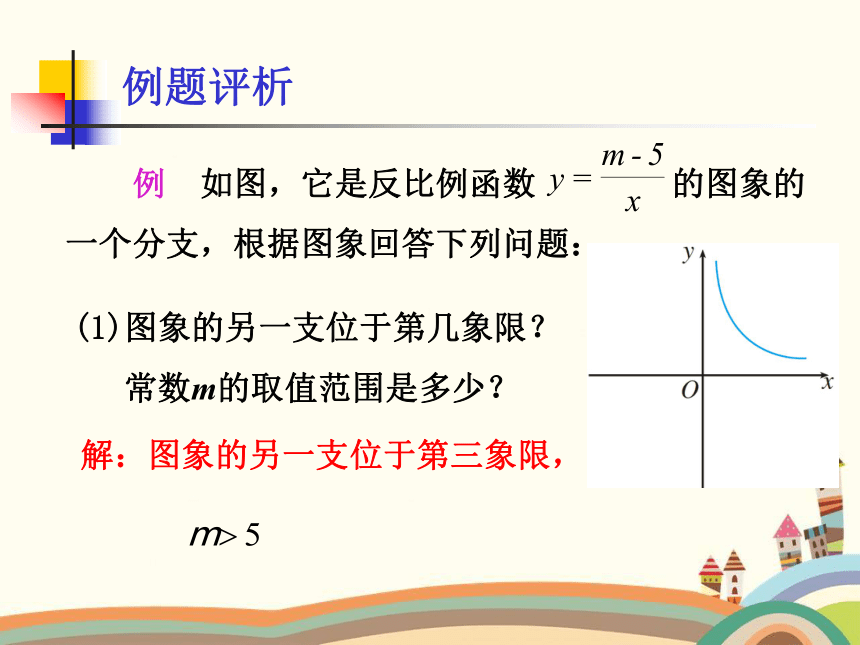
例 如图,它是反比例函数 的图象的一个分支,根据图象回答下列问题:
(1)图象的另一支位于第几象限?
常数m的取值范围是多少?
解:图象的另一支位于第三象限,
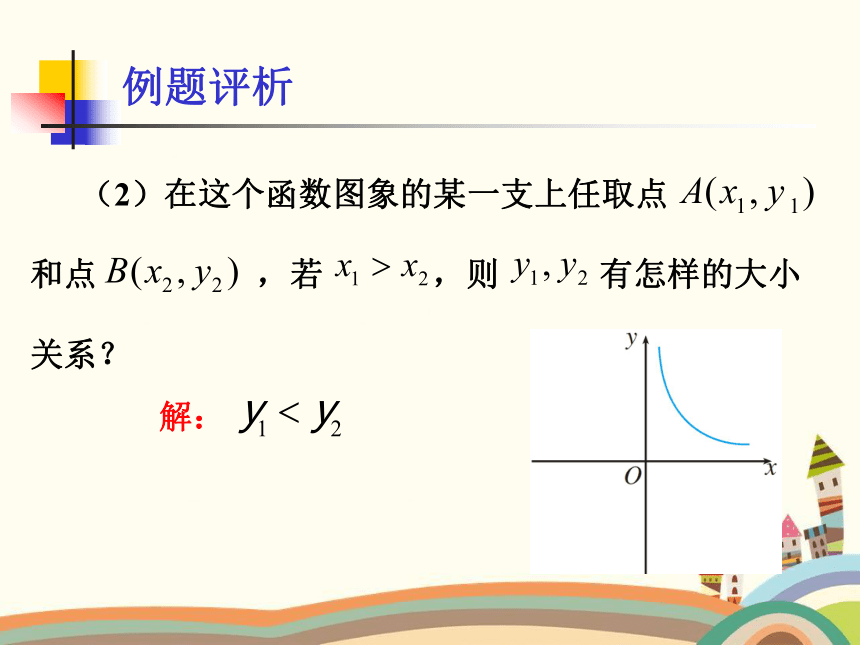
(2)在这个函数图象的某一支上任取点
和点 ,若 ,则 有怎样的大小关系?
解:
例题评析
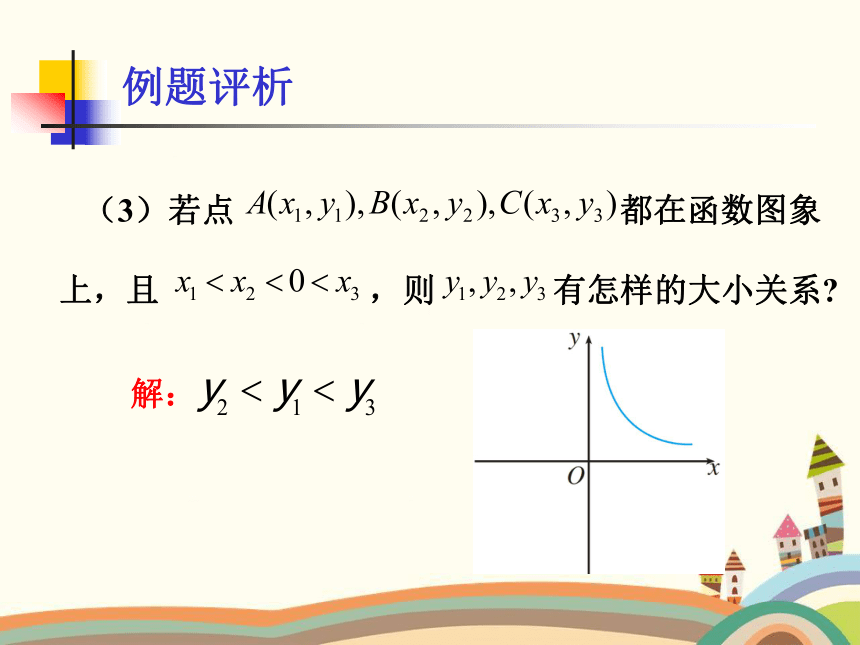
(3)若点 都在函数图象上,且 ,则 有怎样的大小关系
解:
例题评析
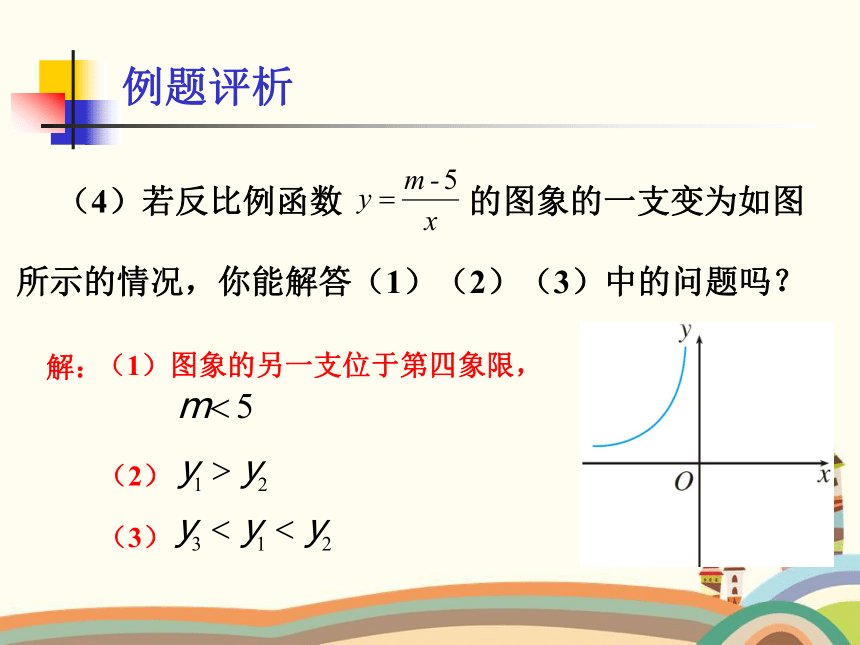
(4)若反比例函数 的图象的一支变为如图所示的情况,你能解答(1)(2)(3)中的问题吗?
(2)
(3)
(1)图象的另一支位于第四象限,
解:
例题评析
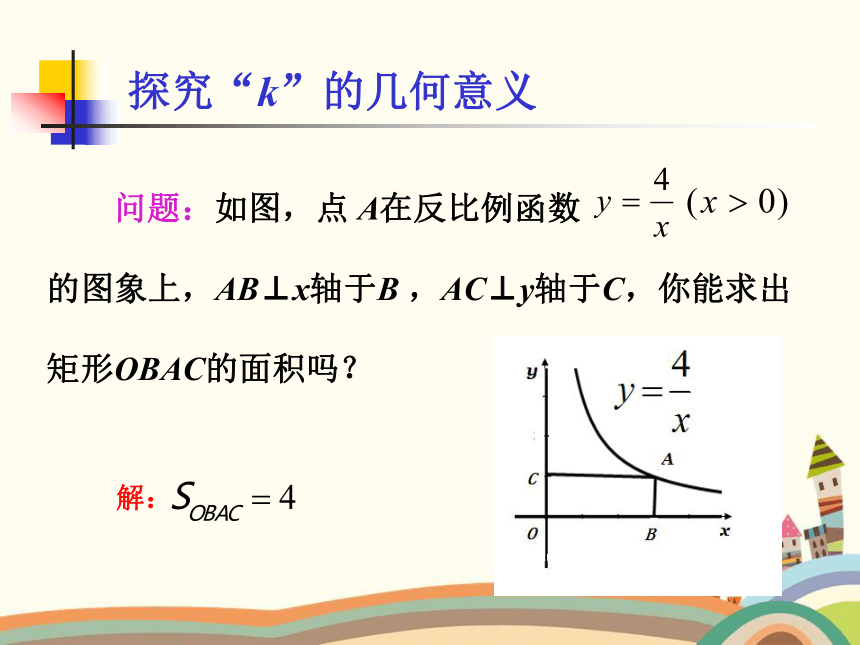
探究“k”的几何意义
问题:如图,点 A在反比例函数 的图象上,AB⊥x轴于B ,AC⊥y轴于C,你能求出矩形OBAC的面积吗?
解:
变式1:如图,点 A在反比例函数 的图象上,AB⊥ x 轴于B ,AC⊥ y轴于C,若A在图象上运动,矩形OBAC面积会变化吗?
不变
解:
探究“k”的几何意义
变式2:若点A在 的图象上呢?
不变
解:
探究“k”的几何意义
变式3:如图,若点A是 的图象上任意一点呢?
解:
探究“k”的几何意义
课堂练习
1.写出函数解析式表示下列关系,并指出它们各是什么函数:
(1)体积是常数V时,圆柱的底面积S与高h 的关系;
(2)柳树乡共有耕地S(单位:hm2),该乡人均耕地面积y(单位:hm2/人)与全乡人口x的关系.
课堂练习
2.下列函数中是反比例函数的是( ).
A.
B.
C.
D.
D
1.已知反比例函数 ,(1)若它的图象在每个象限内,y随自变量x的增大而减小,则实数k的取值范围是 ;(2)若图象经过点(-2,3),则k = .
课堂练习
补充:
2.已知反比例函数 在第一象限的图象如下图,点A在其图象上,点B为x轴正半轴上一点,连接AO,BA,且AO=AB,则 .
课堂练习
6
3.已知反比例函数 图象的一部分如图所示, 直线l⊥x轴于点B,交函数图象于点A,C是y轴上任意一点,S△ABC=1.5,则k的值为 .
课堂练习
-3
4.如图,正比例函数 y1=x 的图象与反比例函数 (k≠ 0)的图象相交于A、B两点,点A的纵坐标为2.
(1)求反比例函数的解析式;
(2)求出点B的坐标,并根据
函数图象,写出当 时,
自变量x的取值范围.
课堂练习
(1) ,(2)B(-2,- 2), x>2或 - 22
5.已知三点(-1,y1)、(2,y2)、(3,y3),
若这三点在函数 的图象上,则y1 、 y2 、y3的大小关系如何?若三点均在函数 的图象上,则y1 、 y2 、 y3的大小关系又如何?(用“>”连接)
答案: y2> y3 > y1; y1> y3 > y2 .
课堂练习
1. k的符号、函数图象所在象限、函数的增减性,三者之间有互推关系,在应用增减性时,尤其注意点是否在同一象限内.
2.面积不变性:从反比例函数 的图象上任一点向两坐标轴作垂线,这一点与两垂足、原点所构成的矩形面积恒为 ,这一点与一垂足、原点所构成的三角形面积恒为 .
课堂小结
布置作业
1.基础题:
教材第9页习题26.1第5、9题.
2.拓展题:
函数 、 和
的图象如图所示,下列命题哪些是正确的?
①如果 ,那么 ;
②如果 ,那么 ;
③如果 ,那么 ;
④如果 ,那么 .
布置作业
第26章 反比例函数
26.1 反比例函数
26.1.2 反比例函数的图象和性质
第2课时 反比例函数的图象和性质的应用
温故引新
问题1:反比例函数的解析式有哪几种 反比例函数有哪些性质
2.当k>0时,在每个象限内y随x的增大而减小;
当k<0时,在每个象限内y随x的增大而增大.
反比例函数解析式有三种:
解:
反比例函数的性质有:
1.它的图象是关于原点中心对称的双曲线.
问题2:已知点(2,-6)在反比例函数的图象上,点(-2,6) 是否也在此图象上?点(-6,2)和(6,-2)呢?
解:点(-2,6), (-6,2)和(6,-2)都
在这个反比例函数图像上.
温故引新
温故引新
阅读教材第7页例3,思考:
(1)确定一个反比例函数的解析式需要什么条件?
已知函数图象上的一个点的坐标即可
(2)如何判断一个点是否在反比例函数的图象上?
看该点的坐标是否满足反比例函数的解析式
例题评析
例 如图,它是反比例函数 的图象的一个分支,根据图象回答下列问题:
(1)图象的另一支位于第几象限?
常数m的取值范围是多少?
解:图象的另一支位于第三象限,
(2)在这个函数图象的某一支上任取点
和点 ,若 ,则 有怎样的大小关系?
解:
例题评析
(3)若点 都在函数图象上,且 ,则 有怎样的大小关系
解:
例题评析
(4)若反比例函数 的图象的一支变为如图所示的情况,你能解答(1)(2)(3)中的问题吗?
(2)
(3)
(1)图象的另一支位于第四象限,
解:
例题评析
探究“k”的几何意义
问题:如图,点 A在反比例函数 的图象上,AB⊥x轴于B ,AC⊥y轴于C,你能求出矩形OBAC的面积吗?
解:
变式1:如图,点 A在反比例函数 的图象上,AB⊥ x 轴于B ,AC⊥ y轴于C,若A在图象上运动,矩形OBAC面积会变化吗?
不变
解:
探究“k”的几何意义
变式2:若点A在 的图象上呢?
不变
解:
探究“k”的几何意义
变式3:如图,若点A是 的图象上任意一点呢?
解:
探究“k”的几何意义
课堂练习
1.写出函数解析式表示下列关系,并指出它们各是什么函数:
(1)体积是常数V时,圆柱的底面积S与高h 的关系;
(2)柳树乡共有耕地S(单位:hm2),该乡人均耕地面积y(单位:hm2/人)与全乡人口x的关系.
课堂练习
2.下列函数中是反比例函数的是( ).
A.
B.
C.
D.
D
1.已知反比例函数 ,(1)若它的图象在每个象限内,y随自变量x的增大而减小,则实数k的取值范围是 ;(2)若图象经过点(-2,3),则k = .
课堂练习
补充:
2.已知反比例函数 在第一象限的图象如下图,点A在其图象上,点B为x轴正半轴上一点,连接AO,BA,且AO=AB,则 .
课堂练习
6
3.已知反比例函数 图象的一部分如图所示, 直线l⊥x轴于点B,交函数图象于点A,C是y轴上任意一点,S△ABC=1.5,则k的值为 .
课堂练习
-3
4.如图,正比例函数 y1=x 的图象与反比例函数 (k≠ 0)的图象相交于A、B两点,点A的纵坐标为2.
(1)求反比例函数的解析式;
(2)求出点B的坐标,并根据
函数图象,写出当 时,
自变量x的取值范围.
课堂练习
(1) ,(2)B(-2,- 2), x>2或 - 2
5.已知三点(-1,y1)、(2,y2)、(3,y3),
若这三点在函数 的图象上,则y1 、 y2 、y3的大小关系如何?若三点均在函数 的图象上,则y1 、 y2 、 y3的大小关系又如何?(用“>”连接)
答案: y2> y3 > y1; y1> y3 > y2 .
课堂练习
1. k的符号、函数图象所在象限、函数的增减性,三者之间有互推关系,在应用增减性时,尤其注意点是否在同一象限内.
2.面积不变性:从反比例函数 的图象上任一点向两坐标轴作垂线,这一点与两垂足、原点所构成的矩形面积恒为 ,这一点与一垂足、原点所构成的三角形面积恒为 .
课堂小结
布置作业
1.基础题:
教材第9页习题26.1第5、9题.
2.拓展题:
函数 、 和
的图象如图所示,下列命题哪些是正确的?
①如果 ,那么 ;
②如果 ,那么 ;
③如果 ,那么 ;
④如果 ,那么 .
布置作业
