正比例和反比例练习课(课件)- 六年级下册数学 青岛版(共16张PPT)
文档属性
| 名称 | 正比例和反比例练习课(课件)- 六年级下册数学 青岛版(共16张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 938.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 青岛版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-07-08 07:10:12 | ||
图片预览






文档简介
(共16张PPT)
正比例和反比例
练习课
什么是正比例关系 什么是反比例关系
分别怎样用字母表示
(1)购买同一种商品的数量和总价如下表:
(2)用同样的钱购买不同的商品的单价和数量如下表:
数量(千克) 1 3 5 7
总价(元) 5 15 25 35
单 价(元) 2 5 10 25
数 量(千克) 50 20 10 4
1.结合意义判断每个表中的两种量成什么关系?
数量变化,总价也随着变化,单价不变,总价和数量的比值一定,总价和数量成正比例关系。
单价变化,数量也随着变化,总价不变,单价和数量的乘积一定,单价和数量成反比例关系。
你能把每种方案的页数补充完整吗
总字数(一定)
=
每页字数×页数
2.一篇文章有12000字,编辑设计了以下几种排版方案。
每页字数 200 300 400 500 600
页 数 60
每页字数与页数成反比例
相同点 不同点
正比例
反比例
1、两种相关联的量;
2、一种量变化,另一种量也随着变化;
3、一种定量
变化趋势
定量
关系式
图像
比值一定
乘积一定
相同
相反
比较正、反比例的异同
3、判断下列各题中的两种量是不是成比例,成什么比例?并说明理由。
(1)天数一定,生产零件的总个数与每天生产零件的个数。
生产零件的总个数
每天生产零件的个数
天数(一定)
=
(4)一个人的年龄和体重。
(5)正方形的边长与周长。
正方形周长
边长
4(一定)
=
(6)圆的直径一定,圆的周长和圆周率。
(2)煤的总量一定,每天的烧煤量与烧的天数
成反比例 每天的烧煤量×烧的天数=煤的总量(一定)
(3)学校计划植500棵树,已植的棵树与未植的棵树
不成比例 已植的棵树+未植的棵树=总棵树(一定)
不成比例 不是相关联的量
成正比例
成正比例
不成比例 圆周率不是变化的量
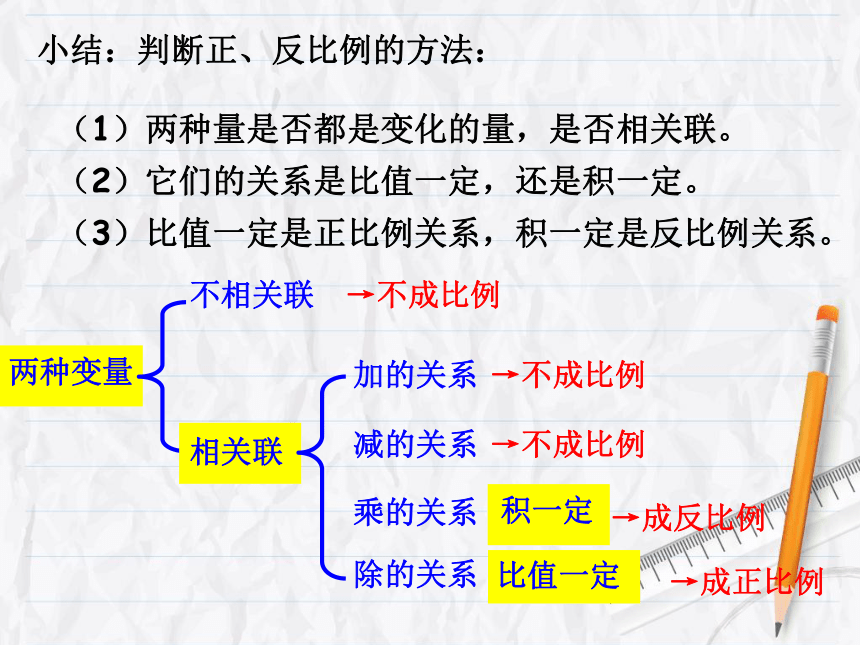
两种变量
不相关联
相关联
加的关系
减的关系
乘的关系
除的关系
→不成比例
→不成比例
→不成比例
积一定
比值一定
→成反比例
→成正比例
小结:判断正、反比例的方法:
(1)两种量是否都是变化的量,是否相关联。
(2)它们的关系是比值一定,还是积一定。
(3)比值一定是正比例关系,积一定是反比例关系。
3、三角形面积一定,底和高成反比例 ( )
5、圆的面积和半径成正比例 ( )
1、长方形的周长一定,长和宽成反比例 ( )
2、长方形的面积一定,长和宽成正比例 ( )
6、圆的周长和半径不成比例 ( )
4、正方形的面积和边长成正比例 ( )
7、如果x与y成反比例,则3x与y成反比例( )
8、铺地面积一定时,方砖边长和所需块数成反比例 ( )
快速判断
×
√
√
×
×
×
√
×
如果 y = 3x,那么x和y成( )比例
如果 ,那么x和y成( )比例
正
反
4、你能根据下面的等式,判断正、反比例吗?
(1)3 a = 2 b,a和b成什么比例?
(2) ,x和y成什么比例?
比值一定,a和b成正比例
x y=2×3=6
乘积一定,x和y成反
比例
4、你能根据下面的等式,判断正、反比例吗?
当 A ÷ B = C 时,
如果B一定,那么A和C成( )比例。
如果A一定,那么B和C成( )比例。
正
B C = A(一定)
反
被除数
除数
商
4、你能根据下面的算式变形,判断正、反比例吗?
5、长方体的体积(V)、底面积(S)和高(h)这三种量
(1)当( )一定时,( )和( )成正比例。
(3)当( )一定时,( )和( )成反比例。
底面积(S)
高(h)
长方体的体积(V)
(2)当( )一定时,( )和( )成正比例。
底面积(S)
高(h)
长方体的体积(V)
长方体的体积(V)
高(h)
底面积(S)
下图是生产某种啤酒时,生产啤酒的总量与所需大麦芽吨数的关系。
1.从图中你可以发现什么?
2.根据上图说一说,7吨大麦芽能生产多少吨啤酒?
3.估计一下,要生产95吨啤酒需要多少吨大麦芽?
70吨
9.5吨
啤酒的总量与所需大麦芽吨数成正比例关系。
你知道吗?生产天数0100200300400500600吨/天102030405060反比例关系也可以用图像表示。如前面研究的每天生产啤酒的吨数和生产天数的关系可以表示为右图。 相同点 不同点
正比例
反比例
1、两种相关联的量;
2、一种量变化,另一种量也随着变化;
3、一种定量
变化趋势
定量
关系式
图像
比值一定
乘积一定
相同
相反
正比例和反比例
练习课
什么是正比例关系 什么是反比例关系
分别怎样用字母表示
(1)购买同一种商品的数量和总价如下表:
(2)用同样的钱购买不同的商品的单价和数量如下表:
数量(千克) 1 3 5 7
总价(元) 5 15 25 35
单 价(元) 2 5 10 25
数 量(千克) 50 20 10 4
1.结合意义判断每个表中的两种量成什么关系?
数量变化,总价也随着变化,单价不变,总价和数量的比值一定,总价和数量成正比例关系。
单价变化,数量也随着变化,总价不变,单价和数量的乘积一定,单价和数量成反比例关系。
你能把每种方案的页数补充完整吗
总字数(一定)
=
每页字数×页数
2.一篇文章有12000字,编辑设计了以下几种排版方案。
每页字数 200 300 400 500 600
页 数 60
每页字数与页数成反比例
相同点 不同点
正比例
反比例
1、两种相关联的量;
2、一种量变化,另一种量也随着变化;
3、一种定量
变化趋势
定量
关系式
图像
比值一定
乘积一定
相同
相反
比较正、反比例的异同
3、判断下列各题中的两种量是不是成比例,成什么比例?并说明理由。
(1)天数一定,生产零件的总个数与每天生产零件的个数。
生产零件的总个数
每天生产零件的个数
天数(一定)
=
(4)一个人的年龄和体重。
(5)正方形的边长与周长。
正方形周长
边长
4(一定)
=
(6)圆的直径一定,圆的周长和圆周率。
(2)煤的总量一定,每天的烧煤量与烧的天数
成反比例 每天的烧煤量×烧的天数=煤的总量(一定)
(3)学校计划植500棵树,已植的棵树与未植的棵树
不成比例 已植的棵树+未植的棵树=总棵树(一定)
不成比例 不是相关联的量
成正比例
成正比例
不成比例 圆周率不是变化的量
两种变量
不相关联
相关联
加的关系
减的关系
乘的关系
除的关系
→不成比例
→不成比例
→不成比例
积一定
比值一定
→成反比例
→成正比例
小结:判断正、反比例的方法:
(1)两种量是否都是变化的量,是否相关联。
(2)它们的关系是比值一定,还是积一定。
(3)比值一定是正比例关系,积一定是反比例关系。
3、三角形面积一定,底和高成反比例 ( )
5、圆的面积和半径成正比例 ( )
1、长方形的周长一定,长和宽成反比例 ( )
2、长方形的面积一定,长和宽成正比例 ( )
6、圆的周长和半径不成比例 ( )
4、正方形的面积和边长成正比例 ( )
7、如果x与y成反比例,则3x与y成反比例( )
8、铺地面积一定时,方砖边长和所需块数成反比例 ( )
快速判断
×
√
√
×
×
×
√
×
如果 y = 3x,那么x和y成( )比例
如果 ,那么x和y成( )比例
正
反
4、你能根据下面的等式,判断正、反比例吗?
(1)3 a = 2 b,a和b成什么比例?
(2) ,x和y成什么比例?
比值一定,a和b成正比例
x y=2×3=6
乘积一定,x和y成反
比例
4、你能根据下面的等式,判断正、反比例吗?
当 A ÷ B = C 时,
如果B一定,那么A和C成( )比例。
如果A一定,那么B和C成( )比例。
正
B C = A(一定)
反
被除数
除数
商
4、你能根据下面的算式变形,判断正、反比例吗?
5、长方体的体积(V)、底面积(S)和高(h)这三种量
(1)当( )一定时,( )和( )成正比例。
(3)当( )一定时,( )和( )成反比例。
底面积(S)
高(h)
长方体的体积(V)
(2)当( )一定时,( )和( )成正比例。
底面积(S)
高(h)
长方体的体积(V)
长方体的体积(V)
高(h)
底面积(S)
下图是生产某种啤酒时,生产啤酒的总量与所需大麦芽吨数的关系。
1.从图中你可以发现什么?
2.根据上图说一说,7吨大麦芽能生产多少吨啤酒?
3.估计一下,要生产95吨啤酒需要多少吨大麦芽?
70吨
9.5吨
啤酒的总量与所需大麦芽吨数成正比例关系。
你知道吗?生产天数0100200300400500600吨/天102030405060反比例关系也可以用图像表示。如前面研究的每天生产啤酒的吨数和生产天数的关系可以表示为右图。 相同点 不同点
正比例
反比例
1、两种相关联的量;
2、一种量变化,另一种量也随着变化;
3、一种定量
变化趋势
定量
关系式
图像
比值一定
乘积一定
相同
相反
