人教版八年级上册12.2 三角形全等的判定课件(共22张PPT)
文档属性
| 名称 | 人教版八年级上册12.2 三角形全等的判定课件(共22张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 605.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-07-08 00:00:00 | ||
图片预览


文档简介
(共22张PPT)
12.2 三角形全等的判定2
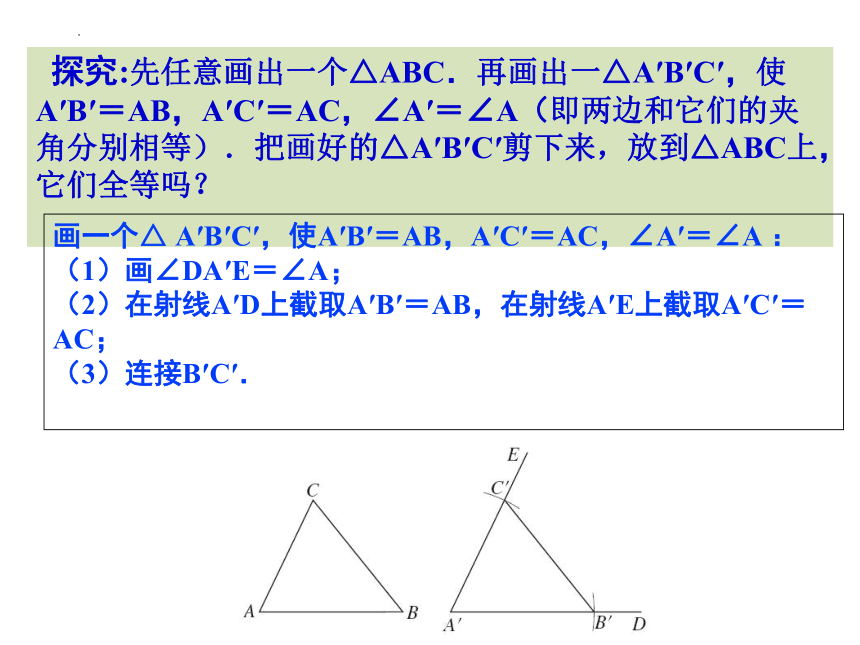
探究:先任意画出一个△ABC.再画出一△A′B′C′,使A′B′=AB,A′C′=AC,∠A′=∠A(即两边和它们的夹角分别相等).把画好的△A′B′C′剪下来,放到△ABC上,它们全等吗?
画一个△ A′B′C′,使A′B′=AB,A′C′=AC,∠A′=∠A :
(1)画∠DA′E=∠A;
(2)在射线A′D上截取A′B′=AB,在射线A′E上截取A′C′=AC;
(3)连接B′C′.
上图给出了画△A′B′C′的方法.你是这样画的吗?探究 3 的结果反映了什么规律?
由探究 3 可以得到以下基本事实,用它可以判定两个三角形全等:
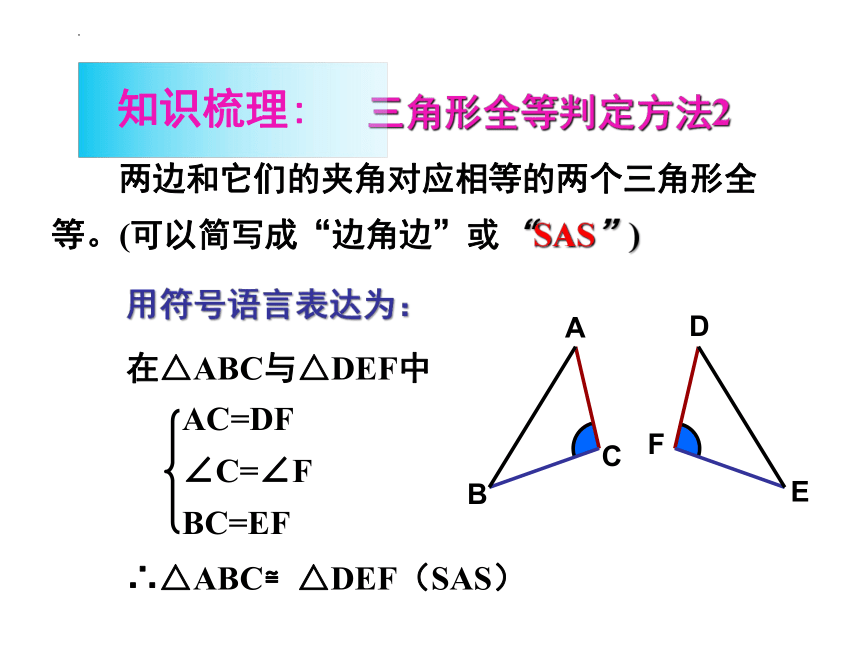
两边和它们的夹角分别相等的两个三角形全等(可以简写成“边角边”或“SAS”).
也就是说,三角形的两条边的长度和它们的夹角的大小确定了,这个三角形的形状、大小就确定了.
三角形全等判定方法2
用符号语言表达为:
在△ABC与△DEF中
∴△ABC≌△DEF(SAS)
两边和它们的夹角对应相等的两个三角形全等。(可以简写成“边角边”或“SAS”)
知识梳理:
F
E
D
C
B
A
AC=DF
∠C=∠F
BC=EF
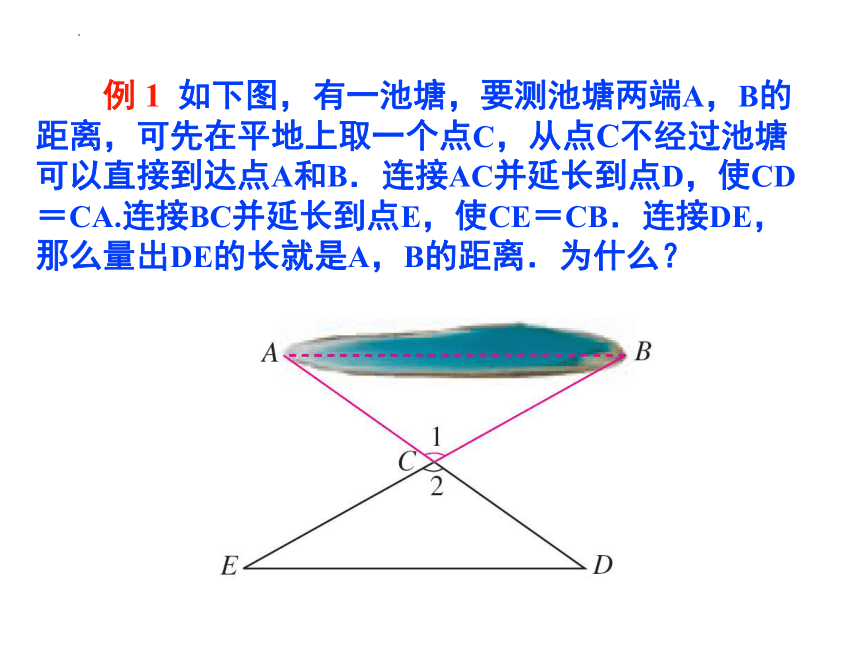
例 1 如下图,有一池塘,要测池塘两端A,B的距离,可先在平地上取一个点C,从点C不经过池塘可以直接到达点A和B.连接AC并延长到点D,使CD=CA.连接BC并延长到点E,使CE=CB.连接DE,那么量出DE的长就是A,B的距离.为什么?
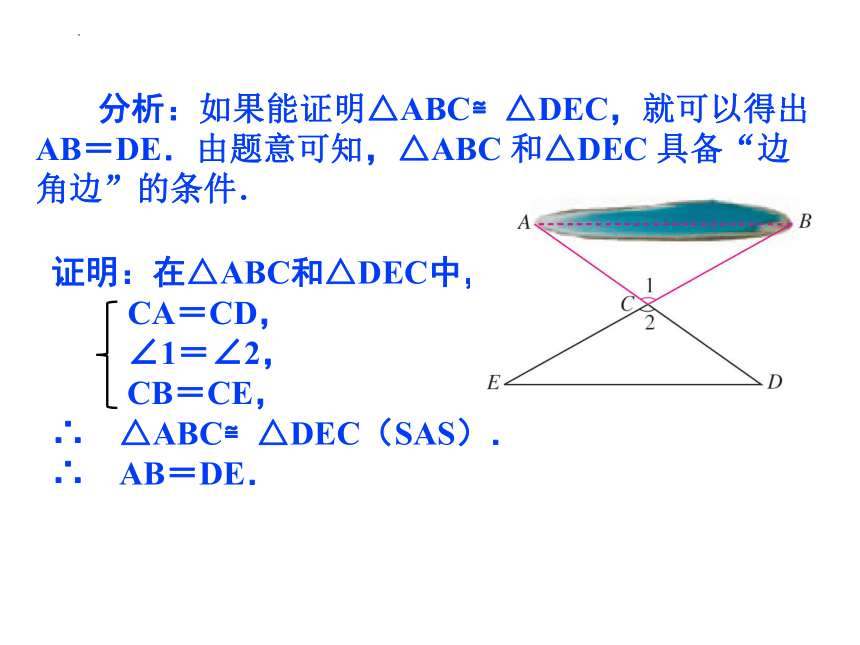
分析:如果能证明△ABC≌△DEC,就可以得出AB=DE.由题意可知,△ABC 和△DEC 具备“边角边”的条件.
证明:在△ABC和△DEC中,
CA=CD,
∠1=∠2,
CB=CE,
∴ △ABC≌△DEC(SAS).
∴ AB=DE.
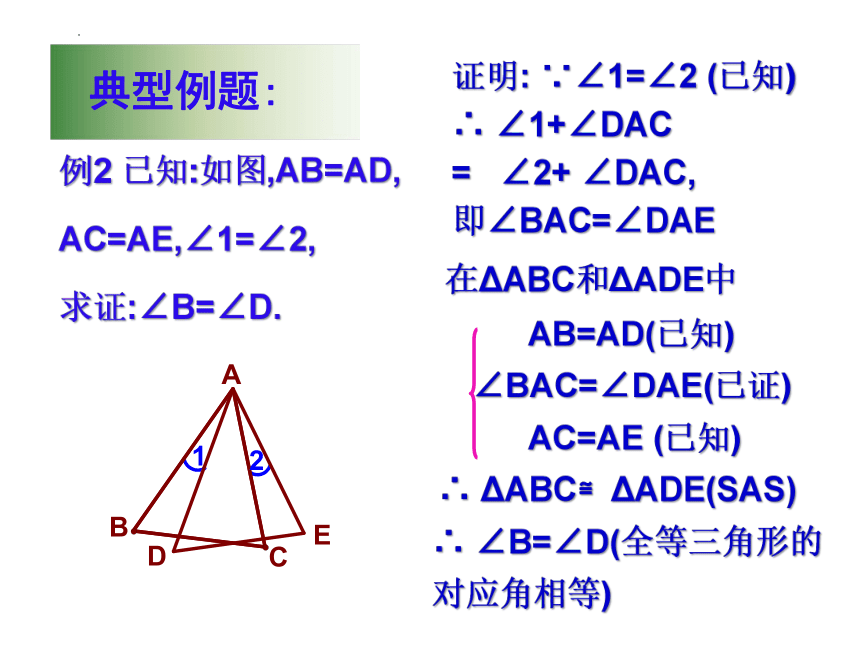
例2 已知:如图,AB=AD,
AC=AE,∠1=∠2,
求证:∠B=∠D.
典型例题:
证明: ∵∠1=∠2 (已知) ∴ ∠1+∠DAC = ∠2+ ∠DAC, 即∠BAC=∠DAE
在ΔABC和ΔADE中
AB=AD(已知)
∠BAC=∠DAE(已证)
AC=AE (已知)
∴ ΔABC≌ΔADE(SAS) ∴ ∠B=∠D(全等三角形的对应角相等)
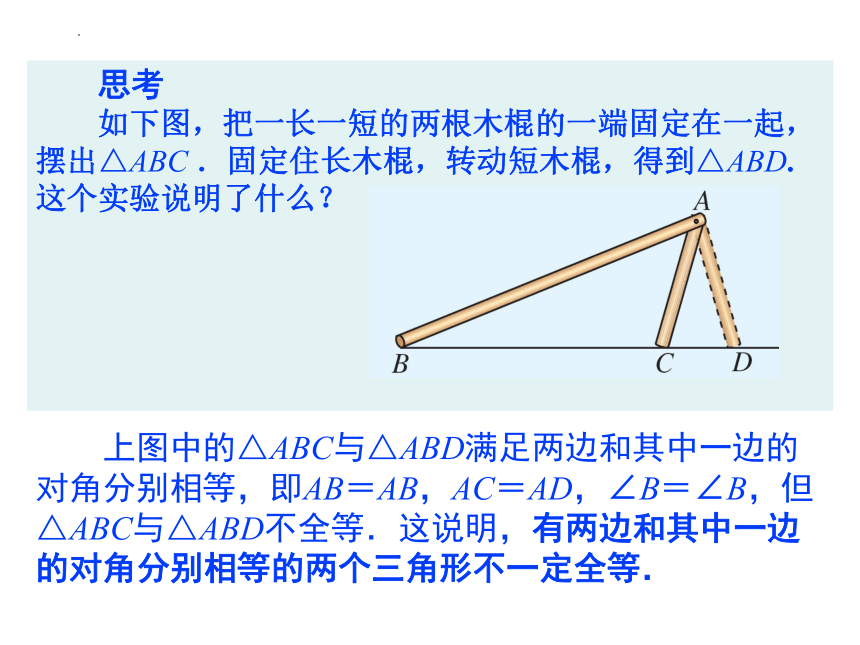
思考
如下图,把一长一短的两根木棍的一端固定在一起,摆出△ABC .固定住长木棍,转动短木棍,得到△ABD. 这个实验说明了什么?
上图中的△ABC与△ABD满足两边和其中一边的对角分别相等,即AB=AB,AC=AD,∠B=∠B,但△ABC与△ABD不全等.这说明,有两边和其中一边的对角分别相等的两个三角形不一定全等.
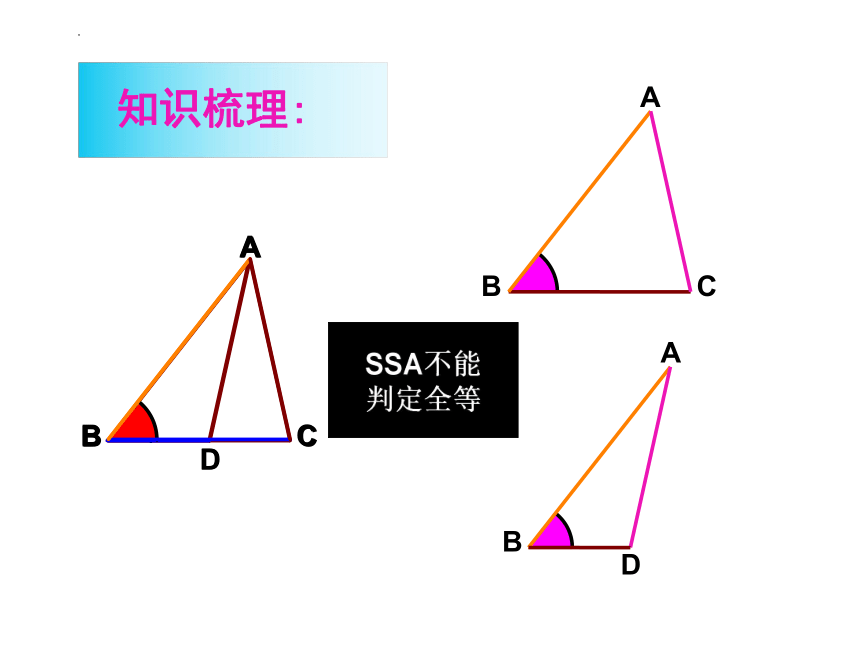
知识梳理:
A
B
D
A
B
C
SSA不能判定全等
如图,两车从南北方向的路段AB的A端出发,分别向东、向西行进相同的距离,到达C,D两地.此时C,D到B的距离相等吗?为什么?
练习
相等.证明如下
在△ABC和△ABD中,
AB=AB,
∠BAC=∠BAD,
AC=AD,
∴ △ABC≌△ABD(SAS).
∴ BC=BD.
知识要点基础练
知识点1 三角形全等的判定方法——“边角边”
1.如图,在△ABC和△DEF中,AB=DE,BC=EF,根据“SAS”判定△ABC≌△DEF,还需添加的条件是 ( B )
A.∠A=∠D B.∠B=∠E
C.∠C=∠F D.以上都可以
知识要点基础练
2.如图,AB,CD相交于点O,且OA=OB.观察图形,图中已具备的另一个相等的条件是 ∠AOD=∠BOC ,联想“SAS”,只需补充条件 OD=OC ,则有△AOD≌△BOC.
知识点2 全等三角形的判定( SAS )的简单应用
3.如图,AC与BD相交于点O,且OA=OC,OD=OB,则AD与BC的位置关系为 平行 .
知识要点基础练
4.如图,点D在AB上,点E在AC上,CD与BE交于点O,且AD=AE,AB=AC,若∠B=20°,则∠C= 20° .
知识要点基础练
5.如图,AB平分∠CAD,AC=AD,求证:BC=BD.
综合能力提升练
6.如图,已知AB∥CD,AB=CD,AE=FD,则图中的全等三角形共有 ( C )
A.1对 B.2对
C.3对 D.4对
7.如图,是工人师傅用同一种材料制成的金属框架,已知∠B=∠E,AB=DE,BF=EC,其中△ABC的周长为24 cm,CF=3 cm,则制成整个金属框架所需这种材料的总长度为 ( A )
A.45 cm B.48 cm
C.51 cm D.54 cm
综合能力提升练
9.如图,在△ABC中,AB=6,BC=5,AC=4,AD平分∠BAC交BC于点D.在AB上截取AE=AC,则△BDE的周长为 7 .
综合能力提升练
10.某大学计划为新生配备如图1所示的折叠凳.图2是折叠凳撑开后的侧面示意图( 木条等材料宽度忽略不计 ),其中凳腿AB和CD的长相等,O是它们的中点.为了使折叠凳坐着舒适,厂家将撑开后的折叠凳宽度AD设计为30 cm,则CB的长度为 30 cm.
综合能力提升练
11.如图,点C,F,E,B在一条直线上,∠CFD=∠BEA,CE=BF,DF=AE.求证:CD∥AB,CD=AB.
综合能力提升练
12.如图,AO是∠BAC和∠DAE的平分线,AD=AE,AB=AC,线段BD和CE是否相等 为什么
综合能力提升练
13.如图,A,F,C,D四点在同一直线上,AF=DC,AB∥DE,且AB=DE.
求证:( 1 )△ABC≌△DEF;
( 2 )∠CBF=∠FEC.
拓展探究突破练
12.2 三角形全等的判定2
探究:先任意画出一个△ABC.再画出一△A′B′C′,使A′B′=AB,A′C′=AC,∠A′=∠A(即两边和它们的夹角分别相等).把画好的△A′B′C′剪下来,放到△ABC上,它们全等吗?
画一个△ A′B′C′,使A′B′=AB,A′C′=AC,∠A′=∠A :
(1)画∠DA′E=∠A;
(2)在射线A′D上截取A′B′=AB,在射线A′E上截取A′C′=AC;
(3)连接B′C′.
上图给出了画△A′B′C′的方法.你是这样画的吗?探究 3 的结果反映了什么规律?
由探究 3 可以得到以下基本事实,用它可以判定两个三角形全等:
两边和它们的夹角分别相等的两个三角形全等(可以简写成“边角边”或“SAS”).
也就是说,三角形的两条边的长度和它们的夹角的大小确定了,这个三角形的形状、大小就确定了.
三角形全等判定方法2
用符号语言表达为:
在△ABC与△DEF中
∴△ABC≌△DEF(SAS)
两边和它们的夹角对应相等的两个三角形全等。(可以简写成“边角边”或“SAS”)
知识梳理:
F
E
D
C
B
A
AC=DF
∠C=∠F
BC=EF
例 1 如下图,有一池塘,要测池塘两端A,B的距离,可先在平地上取一个点C,从点C不经过池塘可以直接到达点A和B.连接AC并延长到点D,使CD=CA.连接BC并延长到点E,使CE=CB.连接DE,那么量出DE的长就是A,B的距离.为什么?
分析:如果能证明△ABC≌△DEC,就可以得出AB=DE.由题意可知,△ABC 和△DEC 具备“边角边”的条件.
证明:在△ABC和△DEC中,
CA=CD,
∠1=∠2,
CB=CE,
∴ △ABC≌△DEC(SAS).
∴ AB=DE.
例2 已知:如图,AB=AD,
AC=AE,∠1=∠2,
求证:∠B=∠D.
典型例题:
证明: ∵∠1=∠2 (已知) ∴ ∠1+∠DAC = ∠2+ ∠DAC, 即∠BAC=∠DAE
在ΔABC和ΔADE中
AB=AD(已知)
∠BAC=∠DAE(已证)
AC=AE (已知)
∴ ΔABC≌ΔADE(SAS) ∴ ∠B=∠D(全等三角形的对应角相等)
思考
如下图,把一长一短的两根木棍的一端固定在一起,摆出△ABC .固定住长木棍,转动短木棍,得到△ABD. 这个实验说明了什么?
上图中的△ABC与△ABD满足两边和其中一边的对角分别相等,即AB=AB,AC=AD,∠B=∠B,但△ABC与△ABD不全等.这说明,有两边和其中一边的对角分别相等的两个三角形不一定全等.
知识梳理:
A
B
D
A
B
C
SSA不能判定全等
如图,两车从南北方向的路段AB的A端出发,分别向东、向西行进相同的距离,到达C,D两地.此时C,D到B的距离相等吗?为什么?
练习
相等.证明如下
在△ABC和△ABD中,
AB=AB,
∠BAC=∠BAD,
AC=AD,
∴ △ABC≌△ABD(SAS).
∴ BC=BD.
知识要点基础练
知识点1 三角形全等的判定方法——“边角边”
1.如图,在△ABC和△DEF中,AB=DE,BC=EF,根据“SAS”判定△ABC≌△DEF,还需添加的条件是 ( B )
A.∠A=∠D B.∠B=∠E
C.∠C=∠F D.以上都可以
知识要点基础练
2.如图,AB,CD相交于点O,且OA=OB.观察图形,图中已具备的另一个相等的条件是 ∠AOD=∠BOC ,联想“SAS”,只需补充条件 OD=OC ,则有△AOD≌△BOC.
知识点2 全等三角形的判定( SAS )的简单应用
3.如图,AC与BD相交于点O,且OA=OC,OD=OB,则AD与BC的位置关系为 平行 .
知识要点基础练
4.如图,点D在AB上,点E在AC上,CD与BE交于点O,且AD=AE,AB=AC,若∠B=20°,则∠C= 20° .
知识要点基础练
5.如图,AB平分∠CAD,AC=AD,求证:BC=BD.
综合能力提升练
6.如图,已知AB∥CD,AB=CD,AE=FD,则图中的全等三角形共有 ( C )
A.1对 B.2对
C.3对 D.4对
7.如图,是工人师傅用同一种材料制成的金属框架,已知∠B=∠E,AB=DE,BF=EC,其中△ABC的周长为24 cm,CF=3 cm,则制成整个金属框架所需这种材料的总长度为 ( A )
A.45 cm B.48 cm
C.51 cm D.54 cm
综合能力提升练
9.如图,在△ABC中,AB=6,BC=5,AC=4,AD平分∠BAC交BC于点D.在AB上截取AE=AC,则△BDE的周长为 7 .
综合能力提升练
10.某大学计划为新生配备如图1所示的折叠凳.图2是折叠凳撑开后的侧面示意图( 木条等材料宽度忽略不计 ),其中凳腿AB和CD的长相等,O是它们的中点.为了使折叠凳坐着舒适,厂家将撑开后的折叠凳宽度AD设计为30 cm,则CB的长度为 30 cm.
综合能力提升练
11.如图,点C,F,E,B在一条直线上,∠CFD=∠BEA,CE=BF,DF=AE.求证:CD∥AB,CD=AB.
综合能力提升练
12.如图,AO是∠BAC和∠DAE的平分线,AD=AE,AB=AC,线段BD和CE是否相等 为什么
综合能力提升练
13.如图,A,F,C,D四点在同一直线上,AF=DC,AB∥DE,且AB=DE.
求证:( 1 )△ABC≌△DEF;
( 2 )∠CBF=∠FEC.
拓展探究突破练
