11.5几何证明举例--三角形全等的判定及应用课件
文档属性
| 名称 | 11.5几何证明举例--三角形全等的判定及应用课件 |

|
|
| 格式 | zip | ||
| 文件大小 | 948.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 青岛版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2013-06-27 00:00:00 | ||
图片预览


文档简介
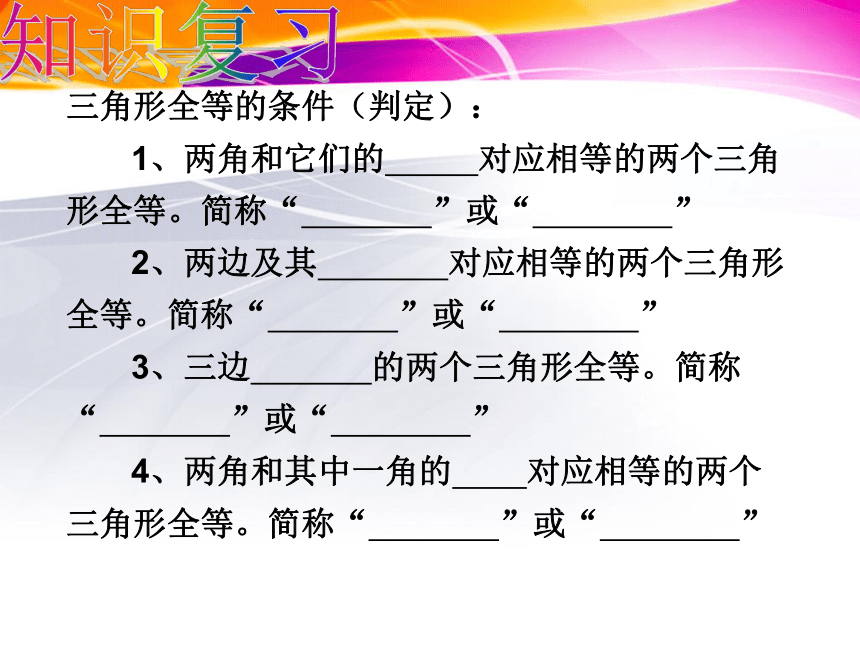
课件29张PPT。三角形全等的判定及应用 11.5几何证明举例全等三角形的对应边相等全等三角形的对应角相等 在三角形全等的前提下我们知道了全等三角形的性质,而在现实中经常存在的问题是,需要我们判断两个三角形是否全等,这时又需要什么条件呢?判断两个三角形是否全等的方法有 。知识复习三角形全等的条件(判定):
1、两角和它们的 对应相等的两个三角形全等。简称“ ”或“ ”
2、两边及其 对应相等的两个三角形全等。简称“ ”或“ ”
3、三边 的两个三角形全等。简称“ ”或“ ”
4、两角和其中一角的 对应相等的两个三角形全等。简称“ ”或“ ”
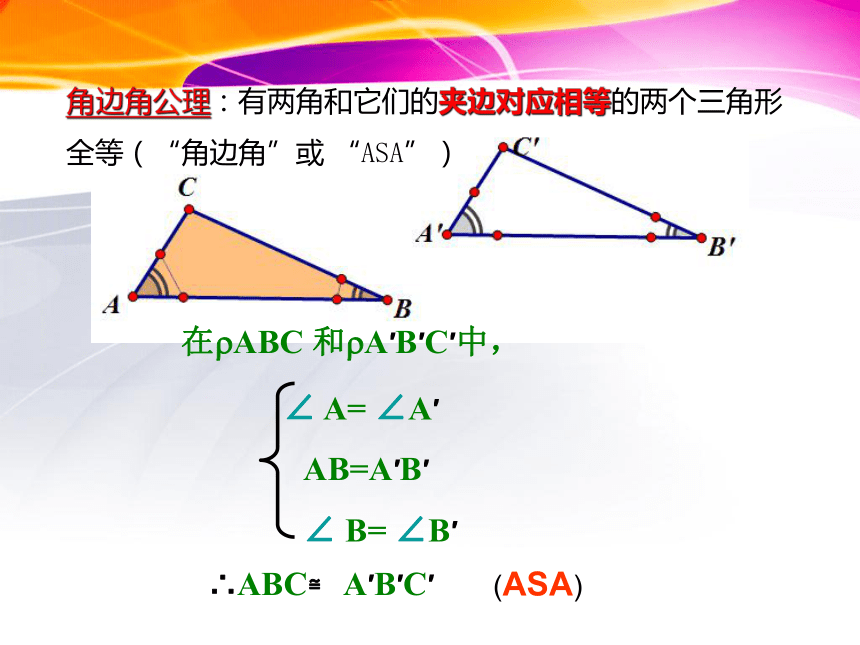
在?ABC 和?A′B′C′中,AB=A′B′∠ A= ∠A′∴ABC≌ A′B′C′(ASA)∠ B= ∠B′角边角公理:有两角和它们的夹边对应相等的两个三角形
全等(“角边角”或 “ASA”)
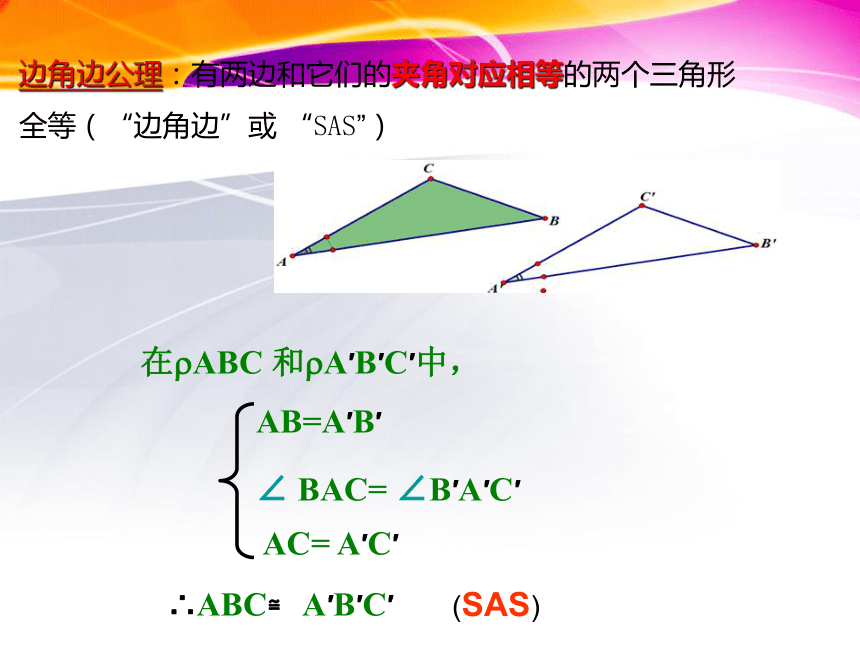
边角边公理:有两边和它们的夹角对应相等的两个三角形
全等(“边角边”或 “SAS”)
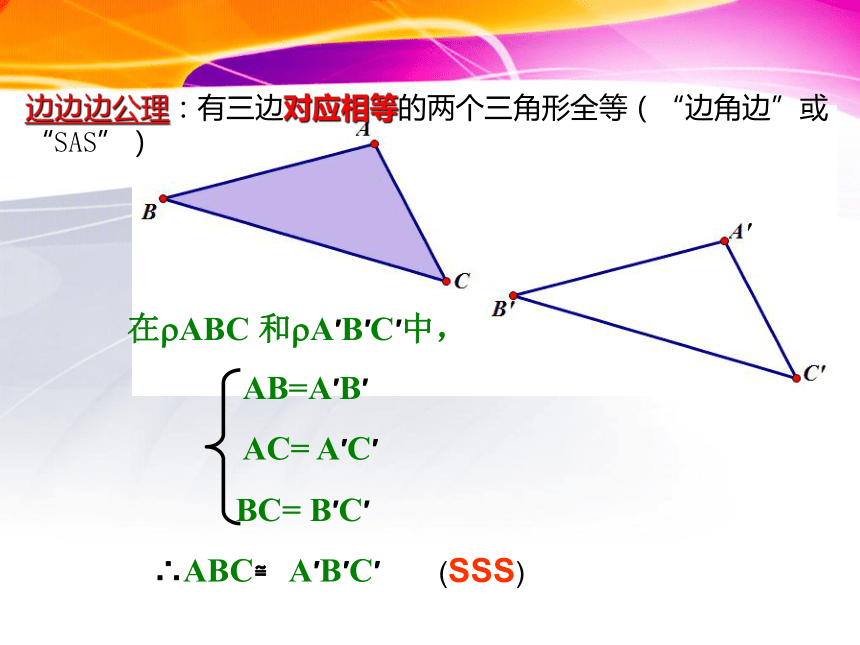
在?ABC 和?A′B′C′中,AB=A′B′AC= A′C′∠ BAC= ∠B′A′C′∴ABC≌ A′B′C′(SAS)在?ABC 和?A′B′C′中,AB=A′B′AC= A′C′BC= B′C′∴ABC≌ A′B′C′(SSS)边边边公理:有三边对应相等的两个三角形全等(“边角边”或 “SAS”)
CABDO
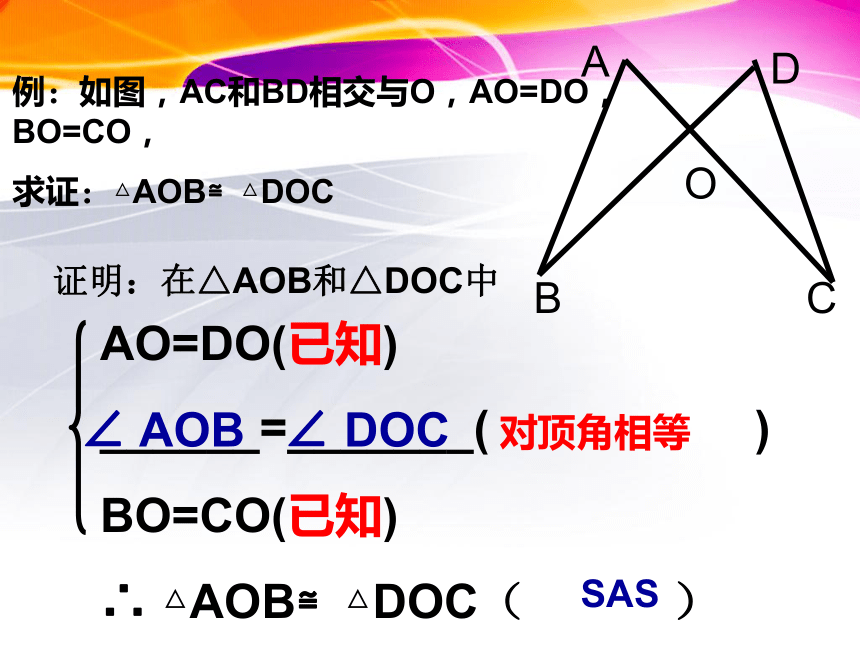
例:如图,AC和BD相交与O,AO=DO,BO=CO,
求证:△AOB≌△DOCAO=DO(已知)
______=_______( )
BO=CO(已知)
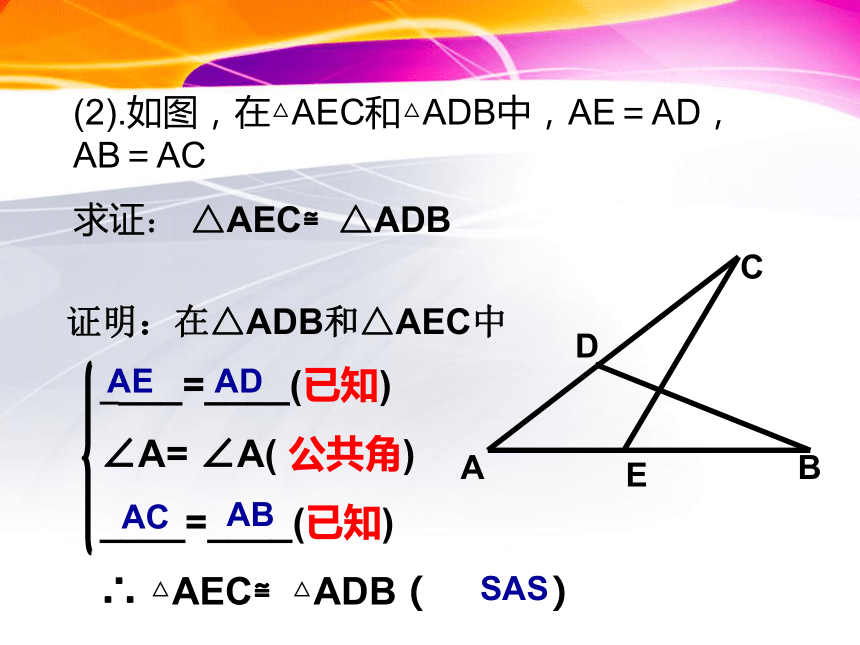
∴ △AOB≌△DOC( )∠ AOB∠ DOC对顶角相等SAS证明:在△AOB和△DOC中(2).如图,在△AEC和△ADB中,AE=AD,AB=AC
求证: △AEC≌△ADB____=____(已知)
∠A= ∠A( 公共角)
____=____(已知)
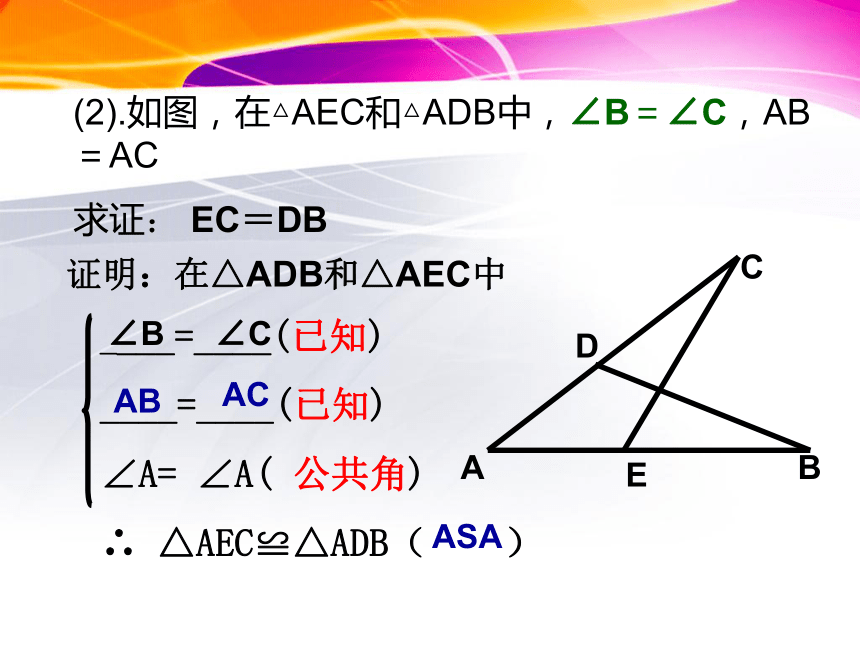
∴ △AEC≌△ADB( )AEADACABSAS证明:在△ADB和△AEC中(2).如图,在△AEC和△ADB中,∠B=∠C,AB=AC
求证: EC=DB____=____(已知)
____=____(已知)
∠A= ∠A( 公共角)
∴ △AEC≌△ADB( )∠B∠CACABASA证明:在△ADB和△AEC中已知: 如图,AC=AD ,∠CAB=∠DAB. 求证: △ACB ≌ △ADB.
ABCD证明:
△ACB ≌ △ADB
这两个条件够吗?
还要什么条件呢?还要一条边已知: 如图,AC=AD ,∠CAB=∠DAB. 求证: △ACB ≌ △ADB.
ABCD它既是△ACB的一条边,看看线段AB又是△ADB的一条边△ACB 和△ADB的公共边已知: 如图,AC=AD ,∠CAB=∠DAB. 求证: △ACB ≌ △ADB.
ABCD证明:在△ACB 和 △ADB中 AC = A D
∠CAB=∠DAB
A B = A B (公共边)∴△ACB≌△ADB(SAS)证明三角形全等的步骤:?1.写出在哪两个三角形中证明全等。(注意把表示对应顶点的字母写在对应的位置上).
?2.按公理(定理)的顺序列出三个条件,用大括号合在一起.
?3.写出结论.每步要有推理的依据.在应用时,怎样寻找已知条件:已知条件包含两部分,一是已知中给出的,二是图形中隐含的(如公共边,公共角、对顶角、邻补角、外角、平角等)所以找条件归结成两句话:已知中找,图形中看.
平面几何中常要说明角相等和线段相等,其说明常用方法:
角相等――对顶角相等;同角(或等角)的余角(或补角)相等;两直线平行,同位角相等,内错角相等;角平分线定义;等式性质;全等三角形的对应角相等.
线段相等的方法――中点定义;全等三角形的对应边相等;等式性质. 1.若AB=AC,则添加什么条件可得△ABD≌ △ACD?△ABD≌ △ACDAD=ADAB=AC∠BAD= ∠CADSAS练习一图中隐含已知条件2.已知如图,点D 在AB上,点E在AC上,BE与CD交于点O,△ABE≌ △ACDSASAB=AC∠A= ∠ AAD=AE要证△ABE≌ △ACD需添加什么条件?隐含条件已知角,缺少两边,而且是与角相邻的两条边!2.已知如图,点D 在AB上,点E在AC上,BE与CD交于点O,SASOB=OC∠BOD= ∠ COEOD=OE要证△BOD≌ △COE需添加什么条件?△BOD≌ △COE隐含条件(对顶角)3.如图,要证△ACB≌ △ADB ,至少选用哪些条件可ABCD△ACB≌ △ADBSAS证得△ACB≌ △ADBAB=AB∠CAB= ∠ DABAC=AD能使用现有条件就应使用现有条件!挖掘隐含条件。3.如图,要证△ACB≌ △ADB ,至少选用哪些条件可ABCD△ACB≌ △ADBSAS证得△ACB≌ △ADBAB=AB∠CBA= ∠ DBABC=BD 1、已知:在△ABE和△ACD中,AB=AC ,AD=AE .
求证:(1)△ ABE≌ △ ACD.
(2)△ OBE≌ △ OCD.
证明: 在△ABE和△ACD 中,AB=ACAD=AE∠A=∠A(公共角)∴ △ ABE ≌ △ ACD(SAS)练习二2、已知:如图,点B,F,C,E在同一直线上,FB=CE,
AB∥ED,AC∥FD,
求证:AB=DE,AC=DF 证明:∵FB=CE(已知) ∴ FB+FC=CE+FC∴BC=EF ∵AB∥ED,AC∥FD(已知) ∴∠B=∠E,∠ACB=∠DFE(两直线平行,内错角相等) 在△ABC与△DEF中{BC=EF(已证)∠B=∠E(已证)∠ACB=∠DFE(已证) ∴△ABC≌△DEF(ASA) ∴AB=DE AC=DF(全等三角形对应边相等)练 习 三已知:如右图,AB、CD相交于点O,AC∥DB,OC = OD, E、F为 AB上两点,且AE = BF.求证:CE=DF.证明:在?AOC 和?BOD中,∵ AC∥DB,∴∠A = ∠B ( 两直线平等,内错角相等 ).又∵ ∠AOC = ∠BOD(对顶角相等)∠A = ∠B ( 已证 ),OC = OD(已知) ∴ ?AOC ≌ ?BOD(AAS) ∴ AC = BD在?AEC 和?BFD中, AC = BD(已证),∠A = ∠B ( 已证 ),AE = BF(已知). ∴ ?AEC ≌ ?BFD(ASA) ∴ CE = DF问题:如图有一池塘。要测池塘两端A、B的距离,可无法直接达到,因此这两点的距离无法直接量出。你能想出办法来吗?ABCED在平地上取一个可直接到达A和B的点C,连结AC并延长至D使CD=CA延长BC并延长至E使CE=CB连结ED,那么量出DE的长,就是A、B的距离.为什么?按图写出“已知”“求证”,并加以证明已知:AD与BE交于点C,CA=CD,CB=CE.求证:AB=DE 练 习 四1、已知:如图,AB=AD,AC=AE,∠1=∠2. 求证:△ABC≌△ADE.2、已知:如图,AE是△ABC的中线,D是 BC延长线上一点,且CD=AB,∠BCA=∠BAC.
求证:AD=2AE. ABCDE【点评】这里∠1和∠2不是所证三角形中的角,∠BAC和∠DAE才是三角形的内角.所以须证∠BAC=∠DAE,才能满足①、②、③三个条件. 【分析】通过添加辅助线,构造全等三角形是一种常用的思考方法.若已知条件中有中线,常延长中线成两倍关系,构成全等三角形. F 【点评】证明一条线段(或一个角)是另一条
线段(或另一个角)的两倍,常用方法是:
(1)加倍法.作出等于短线段(或小角)两倍
的线段(或角),然后证它与较长线段(或较大
角)相等;
(2)折半法.作出较长线段(或较大角)的一
半证明它与较短线段(或较小角)相等. 证明题:1.已知:如图,AD∥BC,AD=CB. 求证:AB=CD. 2.已知: 如图,∠1=∠2,BD=CA.
求证:∠A=∠D. 【提示】 先证ΔABC≌ ΔADC求证:(1)AE=CF; (2)AE∥CF;
(3)∠AFE=∠CEF. 3.已知: 如图,B、F、E、D在一条直线上,
AB=CD,BF=ED,∠B=∠D. 【提示】 先证ΔABE≌ ΔDCF4.已知:如图,ABC为直线,EB⊥AC,
BD=BC,AB=BE.
求证:AF⊥EC. 【提示】求证△ABD≌△EBC,
得∠A=∠E,
因为∠ADB=∠EDF,
∠A+∠ADB=90°,
所以∠E+∠EDF=90°,
AF⊥EC. 小结1.边角边公理(SAS);角边角公理(ASA);边边边公理(SSS);角角边定理(AAS)2.公理的应用中所用到的数学方法:
证明线段(或角相等) 证明线段(或角)所在的两个三角形全等.转化1. 证明两个三角形全等所需的条件应按对应边、对应角、对应边顺序书写.
2. 公理中所出现的边与角必须在所证明的两个三角形中.
3. 公理中涉及的角必须是两边的夹角.DEF思考题:有两边和其中一边的对角对应相等的两个三角形是否全等。
1、两角和它们的 对应相等的两个三角形全等。简称“ ”或“ ”
2、两边及其 对应相等的两个三角形全等。简称“ ”或“ ”
3、三边 的两个三角形全等。简称“ ”或“ ”
4、两角和其中一角的 对应相等的两个三角形全等。简称“ ”或“ ”
在?ABC 和?A′B′C′中,AB=A′B′∠ A= ∠A′∴ABC≌ A′B′C′(ASA)∠ B= ∠B′角边角公理:有两角和它们的夹边对应相等的两个三角形
全等(“角边角”或 “ASA”)
边角边公理:有两边和它们的夹角对应相等的两个三角形
全等(“边角边”或 “SAS”)
在?ABC 和?A′B′C′中,AB=A′B′AC= A′C′∠ BAC= ∠B′A′C′∴ABC≌ A′B′C′(SAS)在?ABC 和?A′B′C′中,AB=A′B′AC= A′C′BC= B′C′∴ABC≌ A′B′C′(SSS)边边边公理:有三边对应相等的两个三角形全等(“边角边”或 “SAS”)
CABDO
例:如图,AC和BD相交与O,AO=DO,BO=CO,
求证:△AOB≌△DOCAO=DO(已知)
______=_______( )
BO=CO(已知)
∴ △AOB≌△DOC( )∠ AOB∠ DOC对顶角相等SAS证明:在△AOB和△DOC中(2).如图,在△AEC和△ADB中,AE=AD,AB=AC
求证: △AEC≌△ADB____=____(已知)
∠A= ∠A( 公共角)
____=____(已知)
∴ △AEC≌△ADB( )AEADACABSAS证明:在△ADB和△AEC中(2).如图,在△AEC和△ADB中,∠B=∠C,AB=AC
求证: EC=DB____=____(已知)
____=____(已知)
∠A= ∠A( 公共角)
∴ △AEC≌△ADB( )∠B∠CACABASA证明:在△ADB和△AEC中已知: 如图,AC=AD ,∠CAB=∠DAB. 求证: △ACB ≌ △ADB.
ABCD证明:
△ACB ≌ △ADB
这两个条件够吗?
还要什么条件呢?还要一条边已知: 如图,AC=AD ,∠CAB=∠DAB. 求证: △ACB ≌ △ADB.
ABCD它既是△ACB的一条边,看看线段AB又是△ADB的一条边△ACB 和△ADB的公共边已知: 如图,AC=AD ,∠CAB=∠DAB. 求证: △ACB ≌ △ADB.
ABCD证明:在△ACB 和 △ADB中 AC = A D
∠CAB=∠DAB
A B = A B (公共边)∴△ACB≌△ADB(SAS)证明三角形全等的步骤:?1.写出在哪两个三角形中证明全等。(注意把表示对应顶点的字母写在对应的位置上).
?2.按公理(定理)的顺序列出三个条件,用大括号合在一起.
?3.写出结论.每步要有推理的依据.在应用时,怎样寻找已知条件:已知条件包含两部分,一是已知中给出的,二是图形中隐含的(如公共边,公共角、对顶角、邻补角、外角、平角等)所以找条件归结成两句话:已知中找,图形中看.
平面几何中常要说明角相等和线段相等,其说明常用方法:
角相等――对顶角相等;同角(或等角)的余角(或补角)相等;两直线平行,同位角相等,内错角相等;角平分线定义;等式性质;全等三角形的对应角相等.
线段相等的方法――中点定义;全等三角形的对应边相等;等式性质. 1.若AB=AC,则添加什么条件可得△ABD≌ △ACD?△ABD≌ △ACDAD=ADAB=AC∠BAD= ∠CADSAS练习一图中隐含已知条件2.已知如图,点D 在AB上,点E在AC上,BE与CD交于点O,△ABE≌ △ACDSASAB=AC∠A= ∠ AAD=AE要证△ABE≌ △ACD需添加什么条件?隐含条件已知角,缺少两边,而且是与角相邻的两条边!2.已知如图,点D 在AB上,点E在AC上,BE与CD交于点O,SASOB=OC∠BOD= ∠ COEOD=OE要证△BOD≌ △COE需添加什么条件?△BOD≌ △COE隐含条件(对顶角)3.如图,要证△ACB≌ △ADB ,至少选用哪些条件可ABCD△ACB≌ △ADBSAS证得△ACB≌ △ADBAB=AB∠CAB= ∠ DABAC=AD能使用现有条件就应使用现有条件!挖掘隐含条件。3.如图,要证△ACB≌ △ADB ,至少选用哪些条件可ABCD△ACB≌ △ADBSAS证得△ACB≌ △ADBAB=AB∠CBA= ∠ DBABC=BD 1、已知:在△ABE和△ACD中,AB=AC ,AD=AE .
求证:(1)△ ABE≌ △ ACD.
(2)△ OBE≌ △ OCD.
证明: 在△ABE和△ACD 中,AB=ACAD=AE∠A=∠A(公共角)∴ △ ABE ≌ △ ACD(SAS)练习二2、已知:如图,点B,F,C,E在同一直线上,FB=CE,
AB∥ED,AC∥FD,
求证:AB=DE,AC=DF 证明:∵FB=CE(已知) ∴ FB+FC=CE+FC∴BC=EF ∵AB∥ED,AC∥FD(已知) ∴∠B=∠E,∠ACB=∠DFE(两直线平行,内错角相等) 在△ABC与△DEF中{BC=EF(已证)∠B=∠E(已证)∠ACB=∠DFE(已证) ∴△ABC≌△DEF(ASA) ∴AB=DE AC=DF(全等三角形对应边相等)练 习 三已知:如右图,AB、CD相交于点O,AC∥DB,OC = OD, E、F为 AB上两点,且AE = BF.求证:CE=DF.证明:在?AOC 和?BOD中,∵ AC∥DB,∴∠A = ∠B ( 两直线平等,内错角相等 ).又∵ ∠AOC = ∠BOD(对顶角相等)∠A = ∠B ( 已证 ),OC = OD(已知) ∴ ?AOC ≌ ?BOD(AAS) ∴ AC = BD在?AEC 和?BFD中, AC = BD(已证),∠A = ∠B ( 已证 ),AE = BF(已知). ∴ ?AEC ≌ ?BFD(ASA) ∴ CE = DF问题:如图有一池塘。要测池塘两端A、B的距离,可无法直接达到,因此这两点的距离无法直接量出。你能想出办法来吗?ABCED在平地上取一个可直接到达A和B的点C,连结AC并延长至D使CD=CA延长BC并延长至E使CE=CB连结ED,那么量出DE的长,就是A、B的距离.为什么?按图写出“已知”“求证”,并加以证明已知:AD与BE交于点C,CA=CD,CB=CE.求证:AB=DE 练 习 四1、已知:如图,AB=AD,AC=AE,∠1=∠2. 求证:△ABC≌△ADE.2、已知:如图,AE是△ABC的中线,D是 BC延长线上一点,且CD=AB,∠BCA=∠BAC.
求证:AD=2AE. ABCDE【点评】这里∠1和∠2不是所证三角形中的角,∠BAC和∠DAE才是三角形的内角.所以须证∠BAC=∠DAE,才能满足①、②、③三个条件. 【分析】通过添加辅助线,构造全等三角形是一种常用的思考方法.若已知条件中有中线,常延长中线成两倍关系,构成全等三角形. F 【点评】证明一条线段(或一个角)是另一条
线段(或另一个角)的两倍,常用方法是:
(1)加倍法.作出等于短线段(或小角)两倍
的线段(或角),然后证它与较长线段(或较大
角)相等;
(2)折半法.作出较长线段(或较大角)的一
半证明它与较短线段(或较小角)相等. 证明题:1.已知:如图,AD∥BC,AD=CB. 求证:AB=CD. 2.已知: 如图,∠1=∠2,BD=CA.
求证:∠A=∠D. 【提示】 先证ΔABC≌ ΔADC求证:(1)AE=CF; (2)AE∥CF;
(3)∠AFE=∠CEF. 3.已知: 如图,B、F、E、D在一条直线上,
AB=CD,BF=ED,∠B=∠D. 【提示】 先证ΔABE≌ ΔDCF4.已知:如图,ABC为直线,EB⊥AC,
BD=BC,AB=BE.
求证:AF⊥EC. 【提示】求证△ABD≌△EBC,
得∠A=∠E,
因为∠ADB=∠EDF,
∠A+∠ADB=90°,
所以∠E+∠EDF=90°,
AF⊥EC. 小结1.边角边公理(SAS);角边角公理(ASA);边边边公理(SSS);角角边定理(AAS)2.公理的应用中所用到的数学方法:
证明线段(或角相等) 证明线段(或角)所在的两个三角形全等.转化1. 证明两个三角形全等所需的条件应按对应边、对应角、对应边顺序书写.
2. 公理中所出现的边与角必须在所证明的两个三角形中.
3. 公理中涉及的角必须是两边的夹角.DEF思考题:有两边和其中一边的对角对应相等的两个三角形是否全等。
同课章节目录
- 第6章 平行四边形
- 6.1 平行四边形及其性质
- 6.2 平行四边形的判定
- 6.3 特殊的平行四边形
- 6.4 三角形的中位线定理
- 第7章 实数
- 7.1 算术平方根
- 7.2 勾股定理
- 7.3 根号2是有理数吗
- 7.4 勾股定理的逆定理
- 7.5 平方根
- 7.6 立方根
- 7.7 用计算器求平方根和立方根
- 7.8 实数
- 第8章 一元一次不等式
- 8.1 不等式的基本性质
- 8.2 一元一次不等式
- 8.3 列一元一次不等式解应用题
- 8.4 一元一次不等式组
- 第9章 二次根式
- 9.1 二次根式和它的性质
- 9.2 二次根式的加法与减法
- 9.3 二次根式的乘法与除法
- 第10章 一次函数
- 10.1 函数的图像
- 10.2 一次函数和它的图像
- 10.3 一次函数的性质
- 10.4 一次函数与二元一次方程
- 10.5 一次函数与一元一次不等式
- 10.6 一次函数的应用
- 第11章 图形的平移与旋转
- 11.1 图形的平移
- 11.2 图形的旋转
- 11.3 图形的中心对称
