27.2.1相似三角形的判定说课课件
文档属性
| 名称 | 27.2.1相似三角形的判定说课课件 |  | |
| 格式 | zip | ||
| 文件大小 | 803.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 数学 | ||
| 更新时间 | 2013-06-27 20:51:10 | ||
图片预览











文档简介
课件30张PPT。27.2 相似三角形27.2.1 相似三角形的判定义务教育课程标准实验教科书 孝义一中 赵莹莹 九年级下册 说课稿 教材地位
学 情
学习目标
学习重点,难点
教法与学法
教学过程
板书设计
一、说教材地位:
本节课是在前面研究图形的全等
和一些全等变换基础上的拓广和发展,
也是今后学习“投影与视图” 所必须具
备的基础知识。
二、说学情
学生已经学过了图形的全等和全等三
角形,相似多边形的有关知识,也研究了
几种图形的变换。学生对几何图形的观察
和分析能力已初步形成,部分学生解题思
维能力比较高,所以学生对相似三角形的
学习应该是比较轻松的。三.说学习目标:
根据新课标对这部分内容的要求及本课的特点,
结合学生的实情,确定本节课的学习目标为:
1.掌握相似三角形的定义,三角形相似的预备定理
(平行于三角形一边的直线和其它两边相交,所构
成的三角形与原三角形相似),两个三角形相似的
判定定理(如果两个三角形的三组对应边的比相等,
那么这两个三角形相似;如果两个三角形的两组
对应边的比相等,并且相应的夹角相等,那么这两
个三角形相似;)
2.会运用“两个三角形相似的判定定理”和“三角形相似
的预备定理”解决简单的问题.四.说学习重点,难点
重点:掌握两种判定方法,会运用两种
判定方法判定两个三角形相似.
难点:会准确的运用两个三角形相似的
条件来判定三角形是否相似五、说教法、学法:
〈一〉 教法: 数学是一门培养人的思维,发展人的思维的重要
学科,教学中不仅要教知识,更重要的是教方法。因
此,在讲授本节课时,我将采用导学自主法利用导学
案进行教学
〈二〉 学法:
“现代的文盲不是不识字的人,而是没有掌握学习方
法的人。”因而教师要特别注重对学生学法方式的指导。
由于学生都渴望与他人交流,合作探究可使学生感受到
合作的重要和团队的精神力量,增强集体意识,所以本
课分为课前,课中,课后三个阶段,课前让学生自学完
成导学案,课中让学生遵循“小组合作——班级展示——
质疑探究——自悟自得——测评反馈”的主线进行学习,
课后进行反思。 六、说过程
根据新课标中“要引导学生投入到
探索与交流的学习活动中”的教学要求,
设计如下教学过程: (一)课前
教师发导学案,明确自学范围。
设计意图:
此环节为课堂上师生互动,学生自主,
小组探究等提供了强有力的保证。
(二)课中
结合本节的教学内容,学生的实际情况,我
设计了以下五个主要的教学环节。
1.导入新课
通过相似多边形的定义让学生类比猜测什么是
相似三角形,从而引出本节课题:相似三角形的
判定
设计意图:
此环节体现出了新课标中要求教学设计要从学
生已有的认知结构出发,注重新旧知识之间的联系。2.小组合作
自学课本41页“思考”部分开始到44页“探
究3”止,结合自学情况对导学案中的1---7题
分小组进行交流,合作解决自学中存在的疑惑。
设计意图:
此环节是为了体现以学生发展为本,让学生
参与,让他们善于抓住学习过程中的困难,通
过合作交流,学一家,融百家,成自家,从而
达到解决问题的目的。3.班级展示
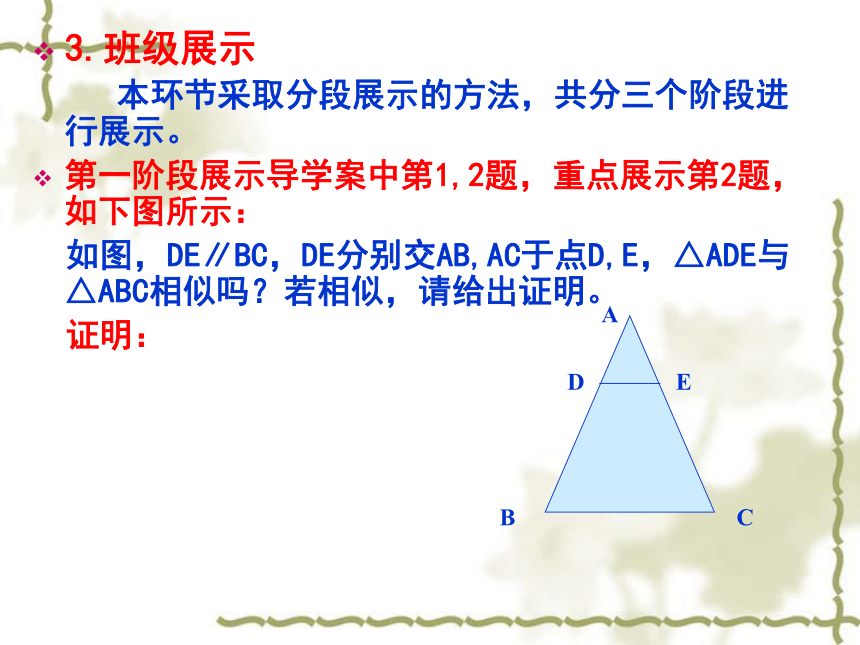
本环节采取分段展示的方法,共分三个阶段进行展示。
第一阶段展示导学案中第1,2题,重点展示第2题,如下图所示:
如图,DE∥BC,DE分别交AB,AC于点D,E,△ADE与△ABC相似吗?若相似,请给出证明。
证明:ABCDE
由此得到结论: 三角形一边的直线和其他两边相交,所构成的三角形与原三角形 。
第二阶段展示导学案中第3,4题,如下图所示:
3.如图△ABC和△A′B′C′中,
AB :A′B′= BC: B′C′=AC :A′C′,
求证 :△ABC~△A′B′C′。
证明:在线段A′B′上截取A′D = AB,
过点D作DE∥B′C′,交A′C′于
点E,可得△A′DE~△A′B′C′.
(请继续完成此题的证明过程)
因此可得结论:如果两个三角形的 _____________ 相等,那么这两个三角形相似;ABCA′B′C′4.如图,△ABC和△A′B′C′中,AB :A′B′= AC :A′C′,
且∠A=∠A′,求证:△ABC~△A′B′C′。
证明:在线段A′B′上截取A′D = AB,
过点D作DE∥B′C′,交A′C′于
点E,可得 △A′DE~△A′B′C′.
(请继续完成此题的证明过程)
因此可得结论:如果两个三角形的------------ 相等,并且 ,那么这两个三角形相似;
在前两个阶段的展示中,分小组选举一
名代表上台展示,最后共同总结相似三角
形的预备定理和判定定理,并说出定理中
的条件结论分别是什么,同时用“因为——,所以——”形式板书出来,强调在今后的
证明中这些结论可以直接运用,并留出时
间让学生重点理解读记。第三阶段展示导学案中5,6,7题,
让学生毛遂自荐上台展示。
5.仿照例1做题: 根据条件,判断△ABC和△A′B′C′是否相似,并说明理由。
(1)∠A=40度,AB=8㎝,AC=15㎝,∠A′=40度,A′B′=16㎝,A′C′=30㎝
(2)AB=10㎝,BC=8㎝,AC=16㎝,A′B′=20㎝, B′C′=16㎝,A′C′=30㎝6.如图,ABC中,点D在BC上,
EF∥BC,分别交AB,AC,AD于点
E,F,G,图中共有————对相
似三角形,分别是—————
7.如图, ∠DAB=∠CAE,请补充
一个条件:———————
使△ADE~△ABC。ABCDEFGABCDE设计意图:
此环节体现出课堂的价值不仅是
让学生学会知识,而且培养学习能力,
提升素质,达到了兵教兵,兵强兵的
目的。4.质疑探究
学生听完小组发言,提出疑惑问题,
由其他小组解决,解决不了的,让学生
共同探究,教师适时点拨。
设计意图:
此环节强调课堂的生成性和精神的
成长性,教师即开发,激励学生进行深
层次多角度的思考与探究。
在上述三个阶段的展示过程中,教
师要做到“无事不出场,非出场时才出场”,把课堂上的主动权交给学生。4.自悟自得
通过本节课的学习,我学会 了 ;
我最感兴趣的是 ;
我想进一步研究的问题是 。
设计意图:
引导学生通过本环节及时回顾整理本节课
所学的知识,培养学生的口头表达能力,训练
发散思维、有效地培养学生的思维品质,提升
其综合素质。5.测评反馈
(1).如图,已知AB:AD=BC:DE=AC:AE,
∠BAD= 20度,求∠CAE的大小.
(2).如图,在△ABC中,D,E分别在AC,AB上,且
AD:AB=AE:AC=1:3,BC=10,则DE的长为多少?
(3).选作题:
要制作两个形状相同的三角形框架,其中一个三角形框架的三边长分别为4,5,6,另一个三角形框架的一边长为2,它的另两条边长应当是 ABCDEEABCD设计意图:
心理学研究表明,学练结合是提高
和深化学生对新知识认识的一个重要途
径,因此在课堂中,让学生在练习中熟
悉定理,分层次布置作业,让不同的学
生在本节课中都有收获。(三)课后
师生进行课后反思,畅所欲言。
设计意图:
此环节是为了总结本节得失,为下节
课积累经验,同时增强学生的反思意识,
培养良好的学习习惯。
相似三角形的判定
1. 平行于 三角形一边的直线和其他两边相交,
所构成的三角形与原三角形 相似 。
∵ DE ∥ BC
∴ △ADE~△ABC
如果两个三角形的 三组对应边的比_____________
2. 相等,那么这两个三角形相似;
∵AB :A′B′= BC: B′C′=AC :A′C′,
∴ △ABC~△A′B′C′
如果两个三角形的 两组对应边的比_
相等,并且相应的夹角相等,那么这
3. 两个三角形相似;
∵ AB :A′B′= AC :A′C′,
∠A=∠A′′
∴ △ABC~△A′B′C
ABCDEABC'
'
'
A'
B'
C'
七.说板书设计设计意图:
板书这样设计能更好引导学生的学习思
路,突出重点难点,形成知识结构,便于
巩固记忆。
总之,本节课我充分调动学生的积极性,让他们探究讨论,上台展示,质疑探究,自悟自得,直至测评反馈,到板书设计,主线贯穿始终,逐一突破重难点,,使学生想,说,讲,做四步合一,既学习了知识,又提高了能力。
学 情
学习目标
学习重点,难点
教法与学法
教学过程
板书设计
一、说教材地位:
本节课是在前面研究图形的全等
和一些全等变换基础上的拓广和发展,
也是今后学习“投影与视图” 所必须具
备的基础知识。
二、说学情
学生已经学过了图形的全等和全等三
角形,相似多边形的有关知识,也研究了
几种图形的变换。学生对几何图形的观察
和分析能力已初步形成,部分学生解题思
维能力比较高,所以学生对相似三角形的
学习应该是比较轻松的。三.说学习目标:
根据新课标对这部分内容的要求及本课的特点,
结合学生的实情,确定本节课的学习目标为:
1.掌握相似三角形的定义,三角形相似的预备定理
(平行于三角形一边的直线和其它两边相交,所构
成的三角形与原三角形相似),两个三角形相似的
判定定理(如果两个三角形的三组对应边的比相等,
那么这两个三角形相似;如果两个三角形的两组
对应边的比相等,并且相应的夹角相等,那么这两
个三角形相似;)
2.会运用“两个三角形相似的判定定理”和“三角形相似
的预备定理”解决简单的问题.四.说学习重点,难点
重点:掌握两种判定方法,会运用两种
判定方法判定两个三角形相似.
难点:会准确的运用两个三角形相似的
条件来判定三角形是否相似五、说教法、学法:
〈一〉 教法: 数学是一门培养人的思维,发展人的思维的重要
学科,教学中不仅要教知识,更重要的是教方法。因
此,在讲授本节课时,我将采用导学自主法利用导学
案进行教学
〈二〉 学法:
“现代的文盲不是不识字的人,而是没有掌握学习方
法的人。”因而教师要特别注重对学生学法方式的指导。
由于学生都渴望与他人交流,合作探究可使学生感受到
合作的重要和团队的精神力量,增强集体意识,所以本
课分为课前,课中,课后三个阶段,课前让学生自学完
成导学案,课中让学生遵循“小组合作——班级展示——
质疑探究——自悟自得——测评反馈”的主线进行学习,
课后进行反思。 六、说过程
根据新课标中“要引导学生投入到
探索与交流的学习活动中”的教学要求,
设计如下教学过程: (一)课前
教师发导学案,明确自学范围。
设计意图:
此环节为课堂上师生互动,学生自主,
小组探究等提供了强有力的保证。
(二)课中
结合本节的教学内容,学生的实际情况,我
设计了以下五个主要的教学环节。
1.导入新课
通过相似多边形的定义让学生类比猜测什么是
相似三角形,从而引出本节课题:相似三角形的
判定
设计意图:
此环节体现出了新课标中要求教学设计要从学
生已有的认知结构出发,注重新旧知识之间的联系。2.小组合作
自学课本41页“思考”部分开始到44页“探
究3”止,结合自学情况对导学案中的1---7题
分小组进行交流,合作解决自学中存在的疑惑。
设计意图:
此环节是为了体现以学生发展为本,让学生
参与,让他们善于抓住学习过程中的困难,通
过合作交流,学一家,融百家,成自家,从而
达到解决问题的目的。3.班级展示
本环节采取分段展示的方法,共分三个阶段进行展示。
第一阶段展示导学案中第1,2题,重点展示第2题,如下图所示:
如图,DE∥BC,DE分别交AB,AC于点D,E,△ADE与△ABC相似吗?若相似,请给出证明。
证明:ABCDE
由此得到结论: 三角形一边的直线和其他两边相交,所构成的三角形与原三角形 。
第二阶段展示导学案中第3,4题,如下图所示:
3.如图△ABC和△A′B′C′中,
AB :A′B′= BC: B′C′=AC :A′C′,
求证 :△ABC~△A′B′C′。
证明:在线段A′B′上截取A′D = AB,
过点D作DE∥B′C′,交A′C′于
点E,可得△A′DE~△A′B′C′.
(请继续完成此题的证明过程)
因此可得结论:如果两个三角形的 _____________ 相等,那么这两个三角形相似;ABCA′B′C′4.如图,△ABC和△A′B′C′中,AB :A′B′= AC :A′C′,
且∠A=∠A′,求证:△ABC~△A′B′C′。
证明:在线段A′B′上截取A′D = AB,
过点D作DE∥B′C′,交A′C′于
点E,可得 △A′DE~△A′B′C′.
(请继续完成此题的证明过程)
因此可得结论:如果两个三角形的------------ 相等,并且 ,那么这两个三角形相似;
在前两个阶段的展示中,分小组选举一
名代表上台展示,最后共同总结相似三角
形的预备定理和判定定理,并说出定理中
的条件结论分别是什么,同时用“因为——,所以——”形式板书出来,强调在今后的
证明中这些结论可以直接运用,并留出时
间让学生重点理解读记。第三阶段展示导学案中5,6,7题,
让学生毛遂自荐上台展示。
5.仿照例1做题: 根据条件,判断△ABC和△A′B′C′是否相似,并说明理由。
(1)∠A=40度,AB=8㎝,AC=15㎝,∠A′=40度,A′B′=16㎝,A′C′=30㎝
(2)AB=10㎝,BC=8㎝,AC=16㎝,A′B′=20㎝, B′C′=16㎝,A′C′=30㎝6.如图,ABC中,点D在BC上,
EF∥BC,分别交AB,AC,AD于点
E,F,G,图中共有————对相
似三角形,分别是—————
7.如图, ∠DAB=∠CAE,请补充
一个条件:———————
使△ADE~△ABC。ABCDEFGABCDE设计意图:
此环节体现出课堂的价值不仅是
让学生学会知识,而且培养学习能力,
提升素质,达到了兵教兵,兵强兵的
目的。4.质疑探究
学生听完小组发言,提出疑惑问题,
由其他小组解决,解决不了的,让学生
共同探究,教师适时点拨。
设计意图:
此环节强调课堂的生成性和精神的
成长性,教师即开发,激励学生进行深
层次多角度的思考与探究。
在上述三个阶段的展示过程中,教
师要做到“无事不出场,非出场时才出场”,把课堂上的主动权交给学生。4.自悟自得
通过本节课的学习,我学会 了 ;
我最感兴趣的是 ;
我想进一步研究的问题是 。
设计意图:
引导学生通过本环节及时回顾整理本节课
所学的知识,培养学生的口头表达能力,训练
发散思维、有效地培养学生的思维品质,提升
其综合素质。5.测评反馈
(1).如图,已知AB:AD=BC:DE=AC:AE,
∠BAD= 20度,求∠CAE的大小.
(2).如图,在△ABC中,D,E分别在AC,AB上,且
AD:AB=AE:AC=1:3,BC=10,则DE的长为多少?
(3).选作题:
要制作两个形状相同的三角形框架,其中一个三角形框架的三边长分别为4,5,6,另一个三角形框架的一边长为2,它的另两条边长应当是 ABCDEEABCD设计意图:
心理学研究表明,学练结合是提高
和深化学生对新知识认识的一个重要途
径,因此在课堂中,让学生在练习中熟
悉定理,分层次布置作业,让不同的学
生在本节课中都有收获。(三)课后
师生进行课后反思,畅所欲言。
设计意图:
此环节是为了总结本节得失,为下节
课积累经验,同时增强学生的反思意识,
培养良好的学习习惯。
相似三角形的判定
1. 平行于 三角形一边的直线和其他两边相交,
所构成的三角形与原三角形 相似 。
∵ DE ∥ BC
∴ △ADE~△ABC
如果两个三角形的 三组对应边的比_____________
2. 相等,那么这两个三角形相似;
∵AB :A′B′= BC: B′C′=AC :A′C′,
∴ △ABC~△A′B′C′
如果两个三角形的 两组对应边的比_
相等,并且相应的夹角相等,那么这
3. 两个三角形相似;
∵ AB :A′B′= AC :A′C′,
∠A=∠A′′
∴ △ABC~△A′B′C
ABCDEABC'
'
'
A'
B'
C'
七.说板书设计设计意图:
板书这样设计能更好引导学生的学习思
路,突出重点难点,形成知识结构,便于
巩固记忆。
总之,本节课我充分调动学生的积极性,让他们探究讨论,上台展示,质疑探究,自悟自得,直至测评反馈,到板书设计,主线贯穿始终,逐一突破重难点,,使学生想,说,讲,做四步合一,既学习了知识,又提高了能力。
