北师大版数学九年级下册 1.1 锐角三角函数第1课时 正切 课件(共21张PPT)
文档属性
| 名称 | 北师大版数学九年级下册 1.1 锐角三角函数第1课时 正切 课件(共21张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 350.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-07-08 14:44:27 | ||
图片预览


文档简介
(共21张PPT)
第1章 直角三角形的边角关系
1.1 锐角三角函数
第1课时 正切
你能比较两个梯子哪个更陡吗?你有哪些办法?
创设问题,导入新课
动手试一试吧!
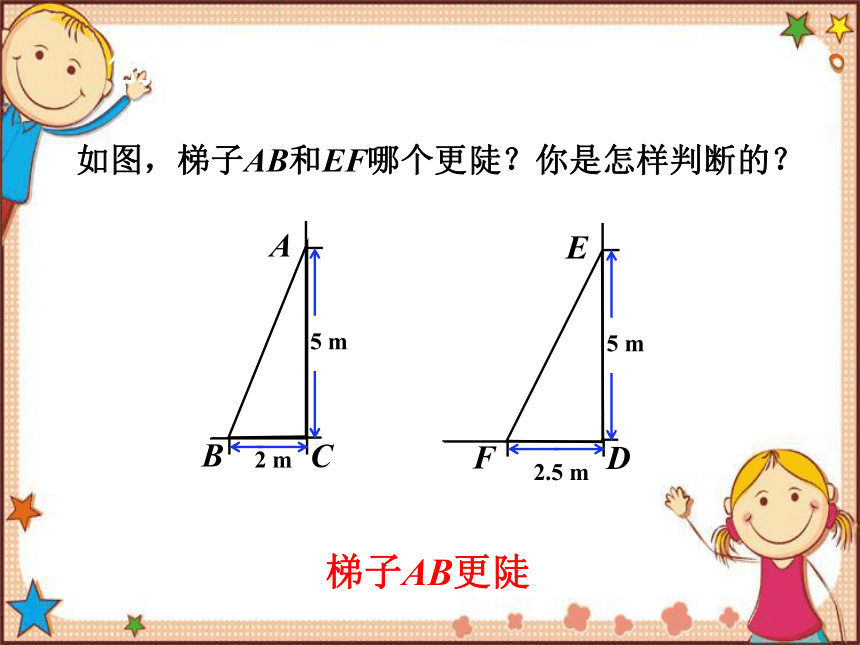
如图,梯子AB和EF哪个更陡?你是怎样判断的?
创设问题,导入新课
A
B
C
2 m
5 m
E
F
D
2.5 m
5 m
梯子AB更陡
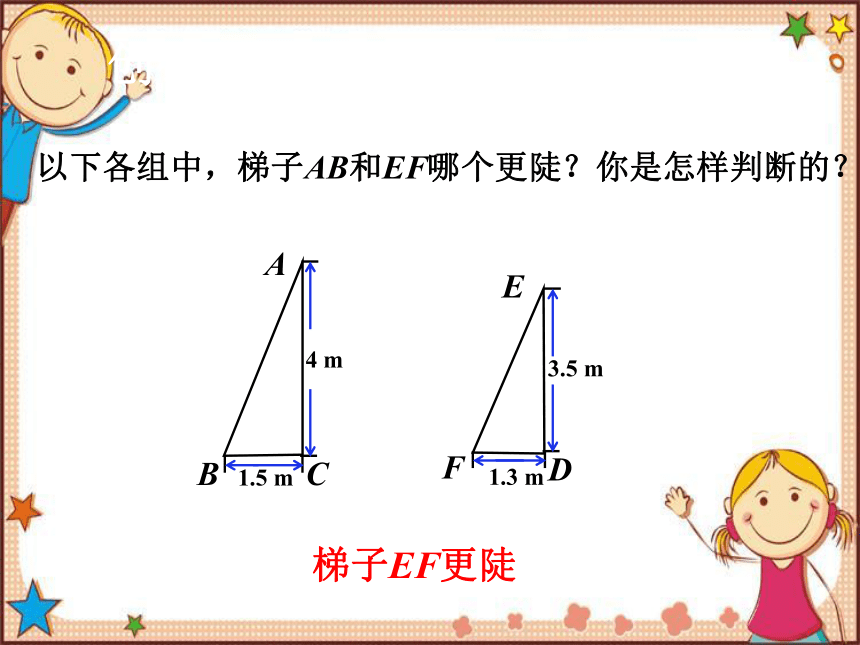
以下各组中,梯子AB和EF哪个更陡?你是怎样判断的?
创设问题,导入新课
A
B
C
1.5 m
4 m
E
F
D
1.3 m
3.5 m
梯子EF更陡
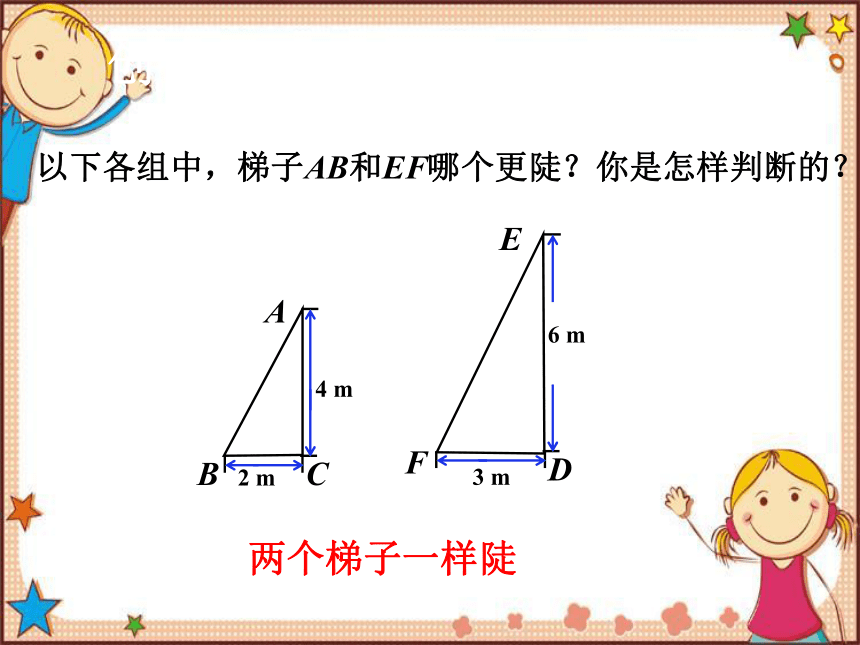
创设问题,导入新课
A
B
C
2 m
4 m
E
F
D
3 m
6 m
两个梯子一样陡
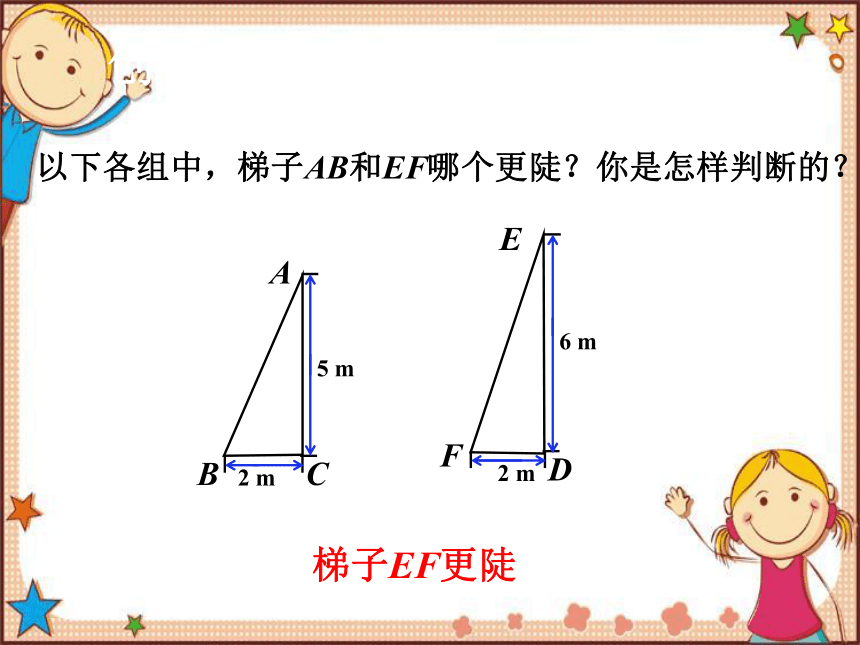
以下各组中,梯子AB和EF哪个更陡?你是怎样判断的?
创设问题,导入新课
A
B
C
2 m
5 m
E
F
D
2 m
6 m
梯子EF更陡
以下各组中,梯子AB和EF哪个更陡?你是怎样判断的?
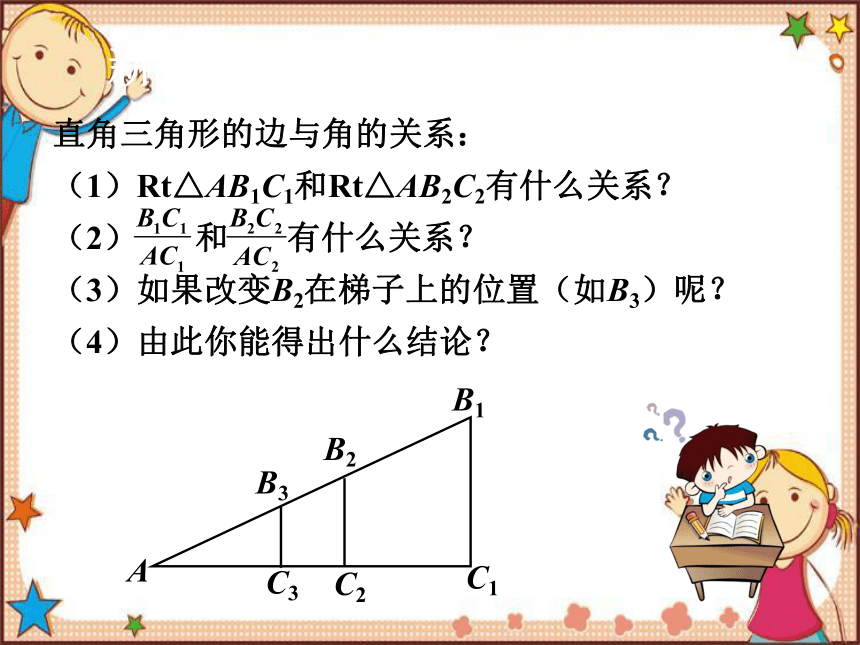
直角三角形的边与角的关系:
(1)Rt△AB1C1和Rt△AB2C2有什么关系?
(2) 和 有什么关系?
(3)如果改变B2在梯子上的位置(如B3)呢?
(4)由此你能得出什么结论?
新课学习
A
B1
B2
B3
C1
C2
C3
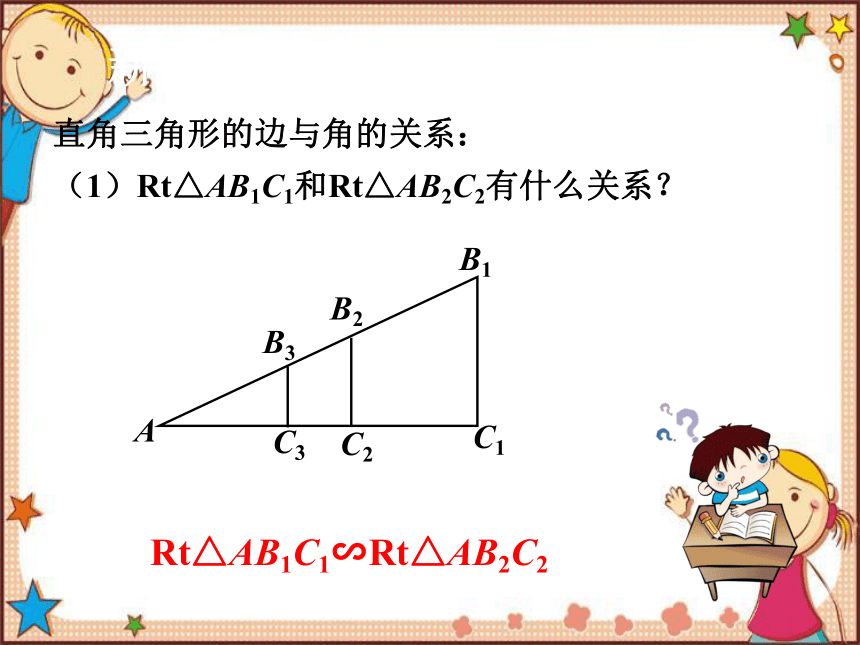
直角三角形的边与角的关系:
(1)Rt△AB1C1和Rt△AB2C2有什么关系?
新课学习
A
B1
B2
B3
C1
C2
C3
Rt△AB1C1∽Rt△AB2C2
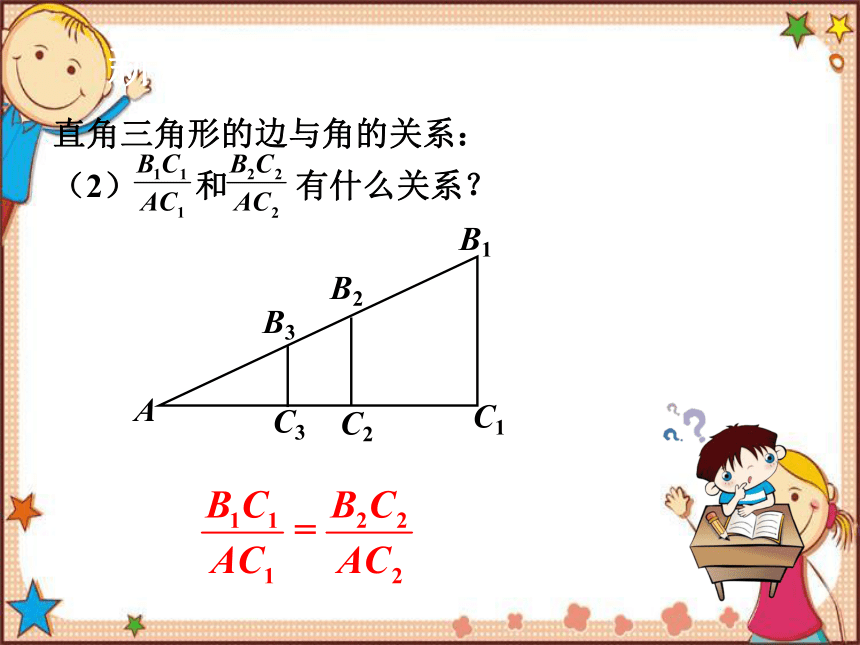
直角三角形的边与角的关系:
(2) 和 有什么关系?
新课学习
A
B1
B2
B3
C1
C2
C3
直角三角形的边与角的关系:
(3)如果改变B2在梯子上的位置(如B3)呢?
新课学习
A
B1
B2
B3
C1
C2
C3
结论仍然成立
Rt△AB1C1∽Rt△AB3C3
直角三角形的边与角的关系:
(4)由此你能得出什么结论?
新课学习
A
B1
B2
B3
C1
C2
C3
一个角的对边与邻边的比值不随边长的改变而改变.
新课学习
定义:如图,在Rt△ABC中,如果锐角A确定,那么∠A的对边与邻边的比便随之确定,这个比叫做∠A的正切,记作tan A,即
A
B
C
∠A的邻边
∠A的对边
例1.如图表示甲、乙两个自动扶梯,哪一个自动扶梯比较陡?
分析:比较哪一个自动扶梯比较陡,实际上就是比较∠α和∠β的正切值的大小.正切值越大,扶梯越陡.
例题感知,体会应用
α
β
4 m
8 m
5 m
13 m
(甲)
(乙)
例1.如图表示甲、乙两个自动扶梯,哪一个自动扶梯比较陡?
解:甲梯中,
乙梯中,
∵
∴甲梯更陡.
例题感知,体会应用
α
β
4 m
8 m
5 m
13 m
(甲)
(乙)
坡度:正切也经常用来描述坡度,例如,有一山坡在水平方向上每前进100 m就升高60 m(如图),那么山坡的坡度就是
例题感知,体会应用
α
60 m
100 m
例2.在Rt△ABC中,∠C=90°,BC=12, AB=20,求tan A和tan B的值.
解:∵在Rt△ABC中, BC=12, AB=20,
∴
∴
例题感知,体会应用
A
B
C
12
20
1.如图,△ABC是等腰三角形,你能根据图中所给数据求出tan C吗
练习巩固
解:
B
A
D
C
1.5
4
A
B
C
2.如图,某人从山脚下的点A走了200 m后到达山顶的点B,已知点B到山脚的垂直距离为55 m,求山的坡度(结果精确到0.001).
练习巩固
解:∵在Rt△ABC中, BC=55, AB=200,
∴
∴
∴山的坡度约是0.286.
1.本节课的主要知识:
(1)正切的定义;(2)正切定义的应用.
2.本节课的困惑:
(1)正切值与角的大小之间的关系;
(2)正切定义的应用.
课堂小结
教材第4~5页习题1.1第1,2,4题.
布置作业
谢谢大家!
再见!
第1章 直角三角形的边角关系
1.1 锐角三角函数
第1课时 正切
你能比较两个梯子哪个更陡吗?你有哪些办法?
创设问题,导入新课
动手试一试吧!
如图,梯子AB和EF哪个更陡?你是怎样判断的?
创设问题,导入新课
A
B
C
2 m
5 m
E
F
D
2.5 m
5 m
梯子AB更陡
以下各组中,梯子AB和EF哪个更陡?你是怎样判断的?
创设问题,导入新课
A
B
C
1.5 m
4 m
E
F
D
1.3 m
3.5 m
梯子EF更陡
创设问题,导入新课
A
B
C
2 m
4 m
E
F
D
3 m
6 m
两个梯子一样陡
以下各组中,梯子AB和EF哪个更陡?你是怎样判断的?
创设问题,导入新课
A
B
C
2 m
5 m
E
F
D
2 m
6 m
梯子EF更陡
以下各组中,梯子AB和EF哪个更陡?你是怎样判断的?
直角三角形的边与角的关系:
(1)Rt△AB1C1和Rt△AB2C2有什么关系?
(2) 和 有什么关系?
(3)如果改变B2在梯子上的位置(如B3)呢?
(4)由此你能得出什么结论?
新课学习
A
B1
B2
B3
C1
C2
C3
直角三角形的边与角的关系:
(1)Rt△AB1C1和Rt△AB2C2有什么关系?
新课学习
A
B1
B2
B3
C1
C2
C3
Rt△AB1C1∽Rt△AB2C2
直角三角形的边与角的关系:
(2) 和 有什么关系?
新课学习
A
B1
B2
B3
C1
C2
C3
直角三角形的边与角的关系:
(3)如果改变B2在梯子上的位置(如B3)呢?
新课学习
A
B1
B2
B3
C1
C2
C3
结论仍然成立
Rt△AB1C1∽Rt△AB3C3
直角三角形的边与角的关系:
(4)由此你能得出什么结论?
新课学习
A
B1
B2
B3
C1
C2
C3
一个角的对边与邻边的比值不随边长的改变而改变.
新课学习
定义:如图,在Rt△ABC中,如果锐角A确定,那么∠A的对边与邻边的比便随之确定,这个比叫做∠A的正切,记作tan A,即
A
B
C
∠A的邻边
∠A的对边
例1.如图表示甲、乙两个自动扶梯,哪一个自动扶梯比较陡?
分析:比较哪一个自动扶梯比较陡,实际上就是比较∠α和∠β的正切值的大小.正切值越大,扶梯越陡.
例题感知,体会应用
α
β
4 m
8 m
5 m
13 m
(甲)
(乙)
例1.如图表示甲、乙两个自动扶梯,哪一个自动扶梯比较陡?
解:甲梯中,
乙梯中,
∵
∴甲梯更陡.
例题感知,体会应用
α
β
4 m
8 m
5 m
13 m
(甲)
(乙)
坡度:正切也经常用来描述坡度,例如,有一山坡在水平方向上每前进100 m就升高60 m(如图),那么山坡的坡度就是
例题感知,体会应用
α
60 m
100 m
例2.在Rt△ABC中,∠C=90°,BC=12, AB=20,求tan A和tan B的值.
解:∵在Rt△ABC中, BC=12, AB=20,
∴
∴
例题感知,体会应用
A
B
C
12
20
1.如图,△ABC是等腰三角形,你能根据图中所给数据求出tan C吗
练习巩固
解:
B
A
D
C
1.5
4
A
B
C
2.如图,某人从山脚下的点A走了200 m后到达山顶的点B,已知点B到山脚的垂直距离为55 m,求山的坡度(结果精确到0.001).
练习巩固
解:∵在Rt△ABC中, BC=55, AB=200,
∴
∴
∴山的坡度约是0.286.
1.本节课的主要知识:
(1)正切的定义;(2)正切定义的应用.
2.本节课的困惑:
(1)正切值与角的大小之间的关系;
(2)正切定义的应用.
课堂小结
教材第4~5页习题1.1第1,2,4题.
布置作业
谢谢大家!
再见!
