人教A版(2019)选择性必修第一册1.1.2空间向量的数量积运算 课件(共30张ppt)
文档属性
| 名称 | 人教A版(2019)选择性必修第一册1.1.2空间向量的数量积运算 课件(共30张ppt) |

|
|
| 格式 | zip | ||
| 文件大小 | 3.6MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-07-08 12:00:21 | ||
图片预览









文档简介
(共30张PPT)
空间向量的数量积运算
复习回顾
1、平面向量数量积的定义:
2、投影向量:
3、向量数量积的性质
4、向量数量积的运算律
O
B
A
O
B
A
由于任意两个空间向量都可以通过平移转化为同一平面内的向量,因此,两个空间向量的夹角和数量积就可以像平面向量那样来定义.
复习回顾
一、空间向量数量积及其计算
定义
性质
运算律
一、空间向量数量积及其计算
规定:零向量与任何向量的数量积都为0
思考1 向量的数量积运算是否满足结合律?
答案 不能,向量没有除法.
答案 不满足结合律,(a·b)·c=a·(b·c)是错误的.
一、空间向量数量积及其计算
例1 如图所示,在棱长为1的正四面体A-BCD中,E,F分别是AB,AD的中点,
求:
=cos 600-cos 600=0.
【练1】(1)已知a=3p-2q,b=p+q,p和q是相互垂直的单位向量,则a·b等于( )
A.1 B.2 C.3 D.4
√
解(1)∵p⊥q且|p|=|q|=1,∴a·b=(3p-2q)·(p+q)=3p2+p·q-2q2=3+0-2=1.
一、空间向量数量积及其计算
=4-0+0-2=2.
2
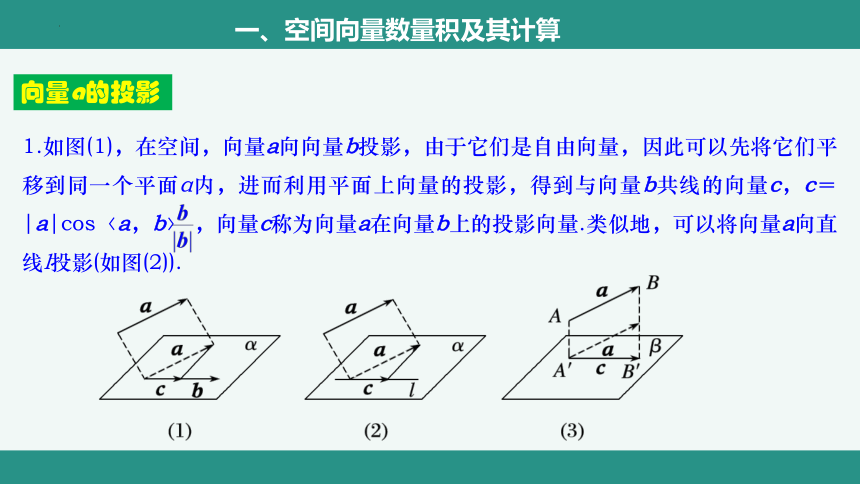
向量a的投影
1.如图(1),在空间,向量a向向量b投影,由于它们是自由向量,因此可以先将它们平移到同一个平面α内,进而利用平面上向量的投影,得到与向量b共线的向量c,c=|a|cos〈a,b〉 ,向量c称为向量a在向量b上的投影向量.类似地,可以将向量a向直线l投影(如图(2)).
一、空间向量数量积及其计算
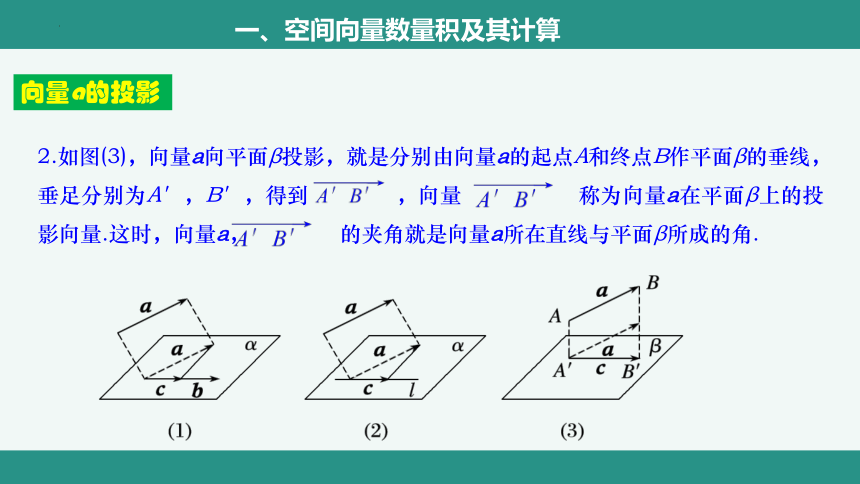
2.如图(3),向量a向平面β投影,就是分别由向量a的起点A和终点B作平面β的垂线,垂足分别为A′,B′,得到 ,向量 称为向量a在平面β上的投影向量.这时,向量a, 的夹角就是向量a所在直线与平面β所成的角.
一、空间向量数量积及其计算
向量a的投影
A
B
C
D
一、空间向量数量积及其计算
二、利用数量积证明垂直问题
二、利用数量积证明垂直问题
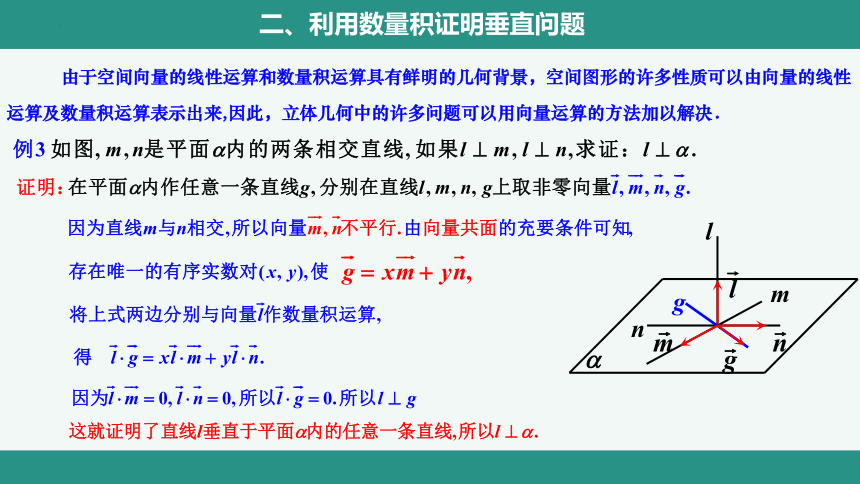
由于空间向量的线性运算和数量积运算具有鲜明的几何背景,空间图形的许多性质可以由向量的线性运算及数量积运算表示出来,因此,立体几何中的许多问题可以用向量运算的方法加以解决.
l
m
n
g
例4 如图所示,在正方体ABCD-A1B1C1D1中,O为AC与BD的交点,G为CC1的中点,
求证:A1O⊥平面GBD.
则a·b=0,b·c=0,a·c=0,|a|=|b|=|c|.
二、利用数量积证明垂直问题
又∵OG∩BD=O,OG 平面GBD,BD 平面GBD,∴A1O⊥平面GBD.
【悟】
用向量法证明几何中垂直关系问题的思路
(1)证直线垂直,可分别构造与两直线平行的向量,证明这两个向量的数量积为0即可.
(2)证线面垂直,需将线面垂直转化为线线垂直,然后利用向量数量积证明线线垂直即可.
二、利用数量积证明垂直问题
【练2】如图所示,在四棱锥P-ABCD中,底面ABCD为平行四边形,∠DAB=60°,AB=2AD,
PD⊥底面ABCD.求证:PA⊥BD.
证:在△ADB中,∠DAB=60°,AB=2AD,
所以AD2+BD2=AB2,
二、利用数量积证明垂直问题
三、用数量积求解夹角和模
三、用数量积求解夹角和模
例5 如图,在直三棱柱ABC-A1B1C1中,CA=CB=1,∠BCA=900,棱AA1=2,点N为
AA1的中点.
三、用数量积求解夹角和模
例5 如图,在直三棱柱ABC-A1B1C1中,CA=CB=1,∠BCA=900,棱AA1=2,点N为
AA1的中点.
例6 如图所示,已知线段AB在平面α内,线段AC⊥α,线段BD⊥AB,且AB=7,
AC=BD=24,线段BD与α所成的角为30°,求CD的长.
三、用数量积求解夹角和模
解 由AC⊥α,可知AC⊥AB,
则∠DBD1为BD与α所成的角,即∠DBD1=300,
过点D作DD1⊥α,D1为垂足,连接BD1,
所以∠BDD1=600,
因为AC⊥α,DD1⊥α,所以AC∥DD1,
因为BD⊥AB,AC⊥AB,
=242+72+242+2×24×24×cos 120°=625,
【悟】
求向量的夹角和模
(2)求线段长度(距离):
①取此线段对应的向量;
②用其他已知夹角和模的向量表示该向量;
③利用|a|= ,计算出|a|,即得所求长度(距离).
三、用数量积求解夹角和模
三、用数量积求解夹角和模
【练3】如图,在直三棱柱ABC-A1B1C1中,若CA=CB=AA1=1,∠BCA=900, 点N为AA1
的中点.求异面直线CA1与AB的夹角.
所以异面直线CA1与AB的夹角为60°.
四、巩固练习
1.已知向量a和b的夹角为120°,且|a|=2,|b|=5,则(2a- b)·a等于( )
√
四、巩固练习
解 (2a-b)·a=2a2-b·a=2|a|2-|a||b|cos 120°
2.已知两异面直线的方向向量分别为a,b,且|a|=|b|=1,a·b= ,则两直线的夹角为( )
A.30° B.60° C.120° D.150°
所以θ=1200,则两个方向向量对应的直线的夹角为1800-1200=60°.
√
四、巩固练习
3.已知空间四边形ABCD的每条边和对角线的长都等于a,点E,F分别是BC,AD的中点,
则 的值为( )
√
4.已知|a|=13,|b|=19,|a+b|=24,则|a-b|=____.
22
解 |a+b|2=a2+2a·b+b2=132+2a·b+192=242,∴2a·b=46,
|a-b|2=a2-2a·b+b2=530-46=484,故|a-b|=22.
5.已知a+3b与7a-5b垂直,且a-4b与7a-2b垂直,则〈a,b〉=_____.
60°
解 由条件知(a+3b)·(7a-5b)=7|a|2-15|b|2+16a·b=0,
代入上面两个式子中的任意一个,得|a|=|b|,
所以〈a,b〉=60°.
四、巩固练习
(a-4b)·(7a-2b)=7|a|2+8|b|2-30a·b=0,两式相减得46a·b=23|b|2,
解 不妨设正方体的棱长为1,
则|a|=|b|=|c|=1,
∴异面直线A1B与AC所成的角为60°.
四、巩固练习
6.如图所示,在正方体ABCD-A1B1C1D1中,求异面直线A1B与AC所成的角.
∴BD⊥PC.
四、巩固练习
7.如图,正四棱锥P-ABCD的各棱长都为a.
(1)用向量法证明BD⊥PC;
=a2+a2+a2+0+2a2cos 600+2a2cos 600=5a2,
课堂小结
作业:
课本P8-9 练习1,2,3,4
本课结束
“
”
空间向量的数量积运算
复习回顾
1、平面向量数量积的定义:
2、投影向量:
3、向量数量积的性质
4、向量数量积的运算律
O
B
A
O
B
A
由于任意两个空间向量都可以通过平移转化为同一平面内的向量,因此,两个空间向量的夹角和数量积就可以像平面向量那样来定义.
复习回顾
一、空间向量数量积及其计算
定义
性质
运算律
一、空间向量数量积及其计算
规定:零向量与任何向量的数量积都为0
思考1 向量的数量积运算是否满足结合律?
答案 不能,向量没有除法.
答案 不满足结合律,(a·b)·c=a·(b·c)是错误的.
一、空间向量数量积及其计算
例1 如图所示,在棱长为1的正四面体A-BCD中,E,F分别是AB,AD的中点,
求:
=cos 600-cos 600=0.
【练1】(1)已知a=3p-2q,b=p+q,p和q是相互垂直的单位向量,则a·b等于( )
A.1 B.2 C.3 D.4
√
解(1)∵p⊥q且|p|=|q|=1,∴a·b=(3p-2q)·(p+q)=3p2+p·q-2q2=3+0-2=1.
一、空间向量数量积及其计算
=4-0+0-2=2.
2
向量a的投影
1.如图(1),在空间,向量a向向量b投影,由于它们是自由向量,因此可以先将它们平移到同一个平面α内,进而利用平面上向量的投影,得到与向量b共线的向量c,c=|a|cos〈a,b〉 ,向量c称为向量a在向量b上的投影向量.类似地,可以将向量a向直线l投影(如图(2)).
一、空间向量数量积及其计算
2.如图(3),向量a向平面β投影,就是分别由向量a的起点A和终点B作平面β的垂线,垂足分别为A′,B′,得到 ,向量 称为向量a在平面β上的投影向量.这时,向量a, 的夹角就是向量a所在直线与平面β所成的角.
一、空间向量数量积及其计算
向量a的投影
A
B
C
D
一、空间向量数量积及其计算
二、利用数量积证明垂直问题
二、利用数量积证明垂直问题
由于空间向量的线性运算和数量积运算具有鲜明的几何背景,空间图形的许多性质可以由向量的线性运算及数量积运算表示出来,因此,立体几何中的许多问题可以用向量运算的方法加以解决.
l
m
n
g
例4 如图所示,在正方体ABCD-A1B1C1D1中,O为AC与BD的交点,G为CC1的中点,
求证:A1O⊥平面GBD.
则a·b=0,b·c=0,a·c=0,|a|=|b|=|c|.
二、利用数量积证明垂直问题
又∵OG∩BD=O,OG 平面GBD,BD 平面GBD,∴A1O⊥平面GBD.
【悟】
用向量法证明几何中垂直关系问题的思路
(1)证直线垂直,可分别构造与两直线平行的向量,证明这两个向量的数量积为0即可.
(2)证线面垂直,需将线面垂直转化为线线垂直,然后利用向量数量积证明线线垂直即可.
二、利用数量积证明垂直问题
【练2】如图所示,在四棱锥P-ABCD中,底面ABCD为平行四边形,∠DAB=60°,AB=2AD,
PD⊥底面ABCD.求证:PA⊥BD.
证:在△ADB中,∠DAB=60°,AB=2AD,
所以AD2+BD2=AB2,
二、利用数量积证明垂直问题
三、用数量积求解夹角和模
三、用数量积求解夹角和模
例5 如图,在直三棱柱ABC-A1B1C1中,CA=CB=1,∠BCA=900,棱AA1=2,点N为
AA1的中点.
三、用数量积求解夹角和模
例5 如图,在直三棱柱ABC-A1B1C1中,CA=CB=1,∠BCA=900,棱AA1=2,点N为
AA1的中点.
例6 如图所示,已知线段AB在平面α内,线段AC⊥α,线段BD⊥AB,且AB=7,
AC=BD=24,线段BD与α所成的角为30°,求CD的长.
三、用数量积求解夹角和模
解 由AC⊥α,可知AC⊥AB,
则∠DBD1为BD与α所成的角,即∠DBD1=300,
过点D作DD1⊥α,D1为垂足,连接BD1,
所以∠BDD1=600,
因为AC⊥α,DD1⊥α,所以AC∥DD1,
因为BD⊥AB,AC⊥AB,
=242+72+242+2×24×24×cos 120°=625,
【悟】
求向量的夹角和模
(2)求线段长度(距离):
①取此线段对应的向量;
②用其他已知夹角和模的向量表示该向量;
③利用|a|= ,计算出|a|,即得所求长度(距离).
三、用数量积求解夹角和模
三、用数量积求解夹角和模
【练3】如图,在直三棱柱ABC-A1B1C1中,若CA=CB=AA1=1,∠BCA=900, 点N为AA1
的中点.求异面直线CA1与AB的夹角.
所以异面直线CA1与AB的夹角为60°.
四、巩固练习
1.已知向量a和b的夹角为120°,且|a|=2,|b|=5,则(2a- b)·a等于( )
√
四、巩固练习
解 (2a-b)·a=2a2-b·a=2|a|2-|a||b|cos 120°
2.已知两异面直线的方向向量分别为a,b,且|a|=|b|=1,a·b= ,则两直线的夹角为( )
A.30° B.60° C.120° D.150°
所以θ=1200,则两个方向向量对应的直线的夹角为1800-1200=60°.
√
四、巩固练习
3.已知空间四边形ABCD的每条边和对角线的长都等于a,点E,F分别是BC,AD的中点,
则 的值为( )
√
4.已知|a|=13,|b|=19,|a+b|=24,则|a-b|=____.
22
解 |a+b|2=a2+2a·b+b2=132+2a·b+192=242,∴2a·b=46,
|a-b|2=a2-2a·b+b2=530-46=484,故|a-b|=22.
5.已知a+3b与7a-5b垂直,且a-4b与7a-2b垂直,则〈a,b〉=_____.
60°
解 由条件知(a+3b)·(7a-5b)=7|a|2-15|b|2+16a·b=0,
代入上面两个式子中的任意一个,得|a|=|b|,
所以〈a,b〉=60°.
四、巩固练习
(a-4b)·(7a-2b)=7|a|2+8|b|2-30a·b=0,两式相减得46a·b=23|b|2,
解 不妨设正方体的棱长为1,
则|a|=|b|=|c|=1,
∴异面直线A1B与AC所成的角为60°.
四、巩固练习
6.如图所示,在正方体ABCD-A1B1C1D1中,求异面直线A1B与AC所成的角.
∴BD⊥PC.
四、巩固练习
7.如图,正四棱锥P-ABCD的各棱长都为a.
(1)用向量法证明BD⊥PC;
=a2+a2+a2+0+2a2cos 600+2a2cos 600=5a2,
课堂小结
作业:
课本P8-9 练习1,2,3,4
本课结束
“
”
