黑龙江省大庆市龙凤区2021-2022学年七年级下学期期末数学试题(word版含答案)
文档属性
| 名称 | 黑龙江省大庆市龙凤区2021-2022学年七年级下学期期末数学试题(word版含答案) |

|
|
| 格式 | docx | ||
| 文件大小 | 1.1MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(五四学制) | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-07-08 00:00:00 | ||
图片预览




文档简介
龙凤区2021-2022学年第二学期期末考试七年级
数学试题
姓名:_________ 班级:_________ 考号:_________
一、选择题:(每题3分,共30分)
1. 在下列实数中:0,,-3.1415,,,0.343343334…(相邻两个4之间3的个数逐次加1),其中无理数有( )
A. 1个 B. 2个 C. 3个 D. 4个
2. 下列计算正确的是( )
A. B. C. D.
3. 下列命题是假命题的是( )
A. 平方根等于本身的数是0; B. 两直线平行,内错角相等;
C. 点到轴的距离为5; D. 数轴上没有点表示这个无理数.
4. 当为何值时,函数是一次函数( )
A. 2 B.-2 C. -2和2 D. 3
5. 已知点,都在直线上,则和的大小关系是( )
A. B. C. D. 无法确定
6. 已知:点与点关于轴对称,则的值为( )
A. 0 B. 1 C. -1 D. 201
7. 如图,在平面直角坐标系中,直线:与直线:交于点,则关于、的方程组的解为( )
A. B. C. D.
8. 在同一直角坐标系中,一次函数和的图象可能正确的是( )
A. B. C. D.
9. 如图,八块相同的长方形地砖拼成一个长方形,每块长方形地砖的长等于( )
A. B. C. D.
10. 如图,图象(折线)描述了一汽车在某一直道上的行驶过程中,汽车离出发地的距离(千米)和行驶时间(小时)之间的函数关系.根据图中提供的信息,给出下列说法:
①汽车共行驶了120千米;
②汽车在行驶途中停留了0.5小时;
③汽车在整个行驶过程中的平均速度为千米/时;
④汽车自出发后3小时至4.5小时之间行驶的速度在逐渐减少.
其中正确的说法有( )
A. 1个 B. 2个 C. 3个 D. 4个
二、填空题:(每题3分,共24分)
11. 的算术平方根是_________.
12. 把命题“对顶角相等”改写成“如果…那么…”的形式_________.
13. 在函数中,自变量的取值范围是_________.
14. 直角三角形的两条边长是4和5,则第三边长是_________.
15. 在平面直角坐标系中,已知点.点,且直线轴,求线段的长_________.
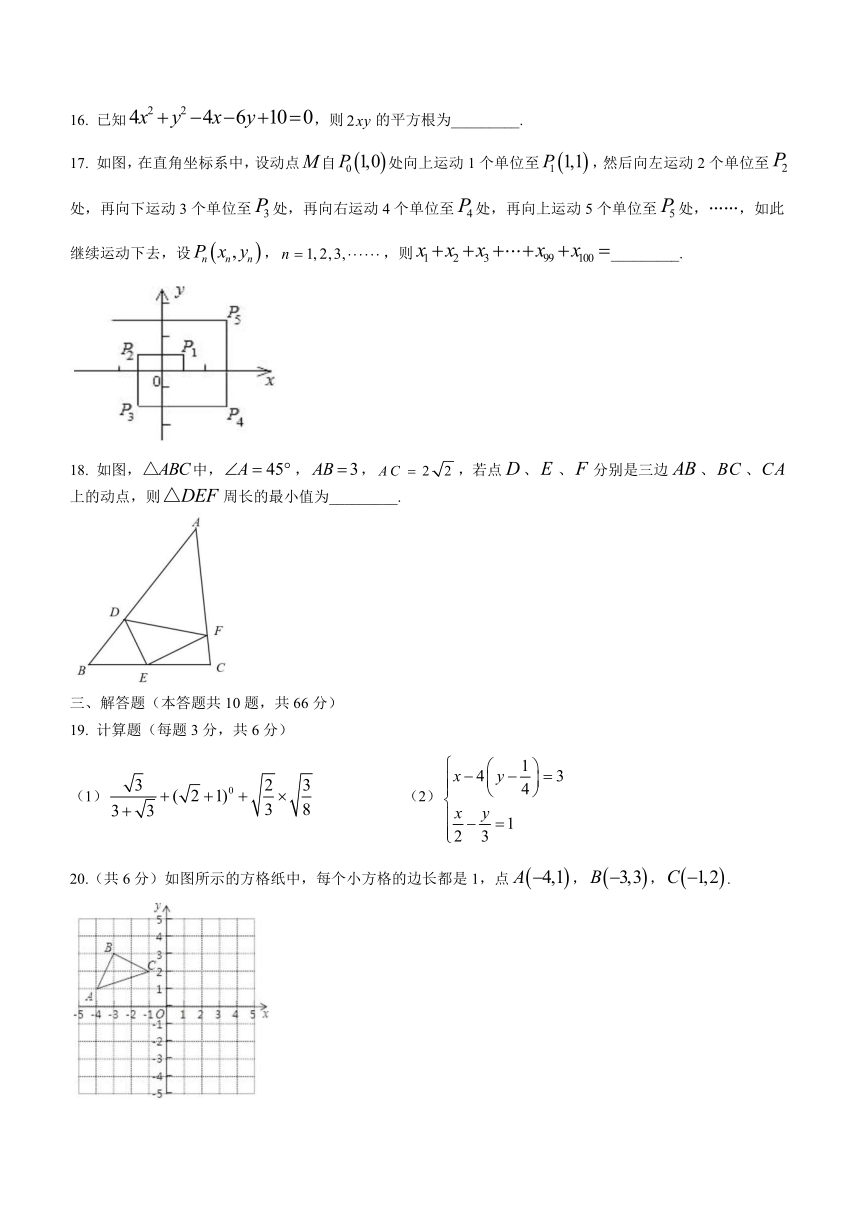
16. 已知,则的平方根为_________.
17. 如图,在直角坐标系中,设动点自处向上运动1个单位至,然后向左运动2个单位至处,再向下运动3个单位至处,再向右运动4个单位至处,再向上运动5个单位至处,……,如此继续运动下去,设,,则_________.
18. 如图,中,,,,若点、、分别是三边、、上的动点,则周长的最小值为_________.
三、解答题(本答题共10题,共66分)
19. 计算题(每题3分,共6分)
(1) (2)
20.(共6分)如图所示的方格纸中,每个小方格的边长都是1,点,,.
(1)作关于轴对称的;
(2)在轴上作出点,使最小,并直接写出点的坐标.
21.(共5分)如图,已知长方形中,,,在边上取一点,将折叠使点恰好落在边上的点,求的长?
22.(共6分)如图,直线经过点和点.
(1)求直线的函数表达式;
(2)求的面积.
23.(共6分)某校举办了国学知识竞赛,满分10分,学生得分均为整数.在初赛中,甲乙两组(每组10人)学生成绩如下(单位:分)
甲组:3,6,6,6,6,6,7,9,9,10
乙组:5,6,6,6,7,7,7,7,8,9
组别 平均数 中位数 众数 方差
甲组 6.8 6 3.76
乙组 7 1.16
(1)以上成绩统计分析表中_________,_________,_________.
(2)小明同学说:“这次竞赛我得了7分,在我们小组中属中游略偏上!”观察上面表格判断,小明可能是__________组的学生;
(3)从平均数和方差看,若从甲乙两组学生中选择一个组参加决赛,应选哪个组?并说明理由.
24.(共6分)甲、乙两车分别从两地同时出发,甲车匀速前往地,乙车匀速前往地,到达地立即以另一速度按原路匀速返回到地,设甲、乙两车离地的路程为(千米),乙车行驶的时间为(时),与之间的函数图象如图所示.
(1)乙车从地到达地的速度是__________千米/时;
(2)乙车到达地时甲车距地的路程是__________千米;
(3)_________;_________.
25.(共8分)如图,四边形中,,,点是的中点,连接,将沿折叠后得到,且点在四边形内部,延长交于点,连接.且.
(1)求证:;
(2)求证:;
(3)若点是的中点,,求的长.
26.(共8分)某景点的门票价格如下表:
购票人数(人) 1~50 51~99 100以上(含100)
门票单价(元) 48 45 42
(1)某校七年级1、2两个班共有102人去游览该景点,其中1班人数少于50人,2班人数多于50人且少于100人.如果两班都以班为单位单独购票,则一共支付4737元,两个班各有多少名学生?
(2)该校八、九年级自愿报名浏览该景点,其中八年级的报名人数不超过50人,九年级的报名人数超过50人,但不超过80人.若两个年级分别购票,总计支付门票费4914元;若合在一起作为一个团体购票,总计支付门票费4452元,问八年级、九年级各报名多少人?
27.(共7分)观察下列式子的变形过程,完成下列任务:
.
类比上述变形过程的基本思路,猜想的结果并验证.
计算:.
28.(共8分)如图,将一张边长为8的正方形纸片放在直角坐标系中,使得与轴重合,与轴重合,点为正方形边上的一点(不与点、点重合).将正方形纸片折叠,使点落在处,点落在处,交于,折痕为.连接、.
初步探究
(1)当时
①直接写出点的坐标;
②求直线的函数表达式.
深入探究
(2)当点在边上移动时,与的度数总是相等,请说明理由.
拓展应用
(3)当点在边上移动时,的周长是否发生变化?并证明你的结论.
龙凤区2021-2022学年第二学期期末考试七年级
数学考试题答案
一、选择题(每题3分共30分)
1 2 3 4 5 6 7 8 9 10
B D D B C C C B D B
二、填空题(每题3分共24分)
11 12 13 14
3 如果两个角是对顶角,那么它们相等 3或
15 16 17 18
3 50
19.计算(6分)
解:(3分)(1) (2)(3分)
20.(1)如图所示,即为所求;
----------3分
(2)作点关于轴的对称点,再连接交轴于点,其坐标为.------3分
21.(5分)∵四边形是矩形,
∴,,
根据题意得:,
∴,,,
设,则,
在中,由勾股定理得:,
即,
∴,
∴,
在中,由勾股定理可得:,
即,
∴,
∴,
即.
故答案为.-------5分
22.(1)设直线的函数表达式为,
因为直线经过点和点,
所以,
解得.
所以直线的函数表达式为.
(2)设直线与轴交于点,则,
所以
.
23.(1)6,-------1分
6.8,-------1分
7;-------1分
(2)甲;-------1分
(3)选乙组参加决赛.理由如下:
∵甲乙两组学生平均数相同,而,
∴乙组的成绩比较稳定,
故选乙组参加决赛.-------2分
24. 解:(1)由图象可得,
乙车从地到地的速度为:(千米/时),
故答案为:120;-------2分
(2)由图象可得,
,
甲车的速度为:(千米/时),
则乙车到达地时甲车距地的路程是(千米),
故答案为:100;-------2分
(3);-------2分
25. 解:(1)可由或证;-------3分
(2)折叠得到,
∴,
∵,,
∴,,
∴四边形为矩形,
∴,
∴;-------2分
(3)∵点是中点,,
∴,
∵点中点,
∴设,则,
则,即,
即,
且,即,
且,即,
∵,,
∴,
∴,
∴,
解得:,即.-------3分
26. 解:(1)设七年级1班有名学生,2班有y名学生,
由题意得:,
解得:,
答:七年级1班有49名学生,2班有53名学生;-------4分
(2)设八年级报名人,九年级报名人,
分两种情况:
①若,
由题意得:,
解得:,(不合题意舍去);
②若,
由题意得:,
解得:,符合题意;
答:八年级报名48人,九年级报名58人.-------4分
27.(1).验证:
;
(2)原式
.
28.(1)①设:,则,,
在中,由勾股定理得:,
即,解得:,
故点.
故答案为:;-------2分
②过点作轴于点,
折叠后点落在处,则点、关于直线对称,则,
∴,而,
∴,
而,,
∴,
∴,
,故点,
将点、的坐标代入一次函数表达式:,
得:,解得:,
故直线的表达式为:;-------2分
(2)∵,
∴.
又∵,
∴.
即.
又∵,
∴,
∴;-------2分
(3)如图,过作,垂足为.
由(1)知,
在和中,
,
∴,
∴,.
又∵,
∴.
又∵,,
∴,
∴,
∴的周长.
故答案为:16.-------2
数学试题
姓名:_________ 班级:_________ 考号:_________
一、选择题:(每题3分,共30分)
1. 在下列实数中:0,,-3.1415,,,0.343343334…(相邻两个4之间3的个数逐次加1),其中无理数有( )
A. 1个 B. 2个 C. 3个 D. 4个
2. 下列计算正确的是( )
A. B. C. D.
3. 下列命题是假命题的是( )
A. 平方根等于本身的数是0; B. 两直线平行,内错角相等;
C. 点到轴的距离为5; D. 数轴上没有点表示这个无理数.
4. 当为何值时,函数是一次函数( )
A. 2 B.-2 C. -2和2 D. 3
5. 已知点,都在直线上,则和的大小关系是( )
A. B. C. D. 无法确定
6. 已知:点与点关于轴对称,则的值为( )
A. 0 B. 1 C. -1 D. 201
7. 如图,在平面直角坐标系中,直线:与直线:交于点,则关于、的方程组的解为( )
A. B. C. D.
8. 在同一直角坐标系中,一次函数和的图象可能正确的是( )
A. B. C. D.
9. 如图,八块相同的长方形地砖拼成一个长方形,每块长方形地砖的长等于( )
A. B. C. D.
10. 如图,图象(折线)描述了一汽车在某一直道上的行驶过程中,汽车离出发地的距离(千米)和行驶时间(小时)之间的函数关系.根据图中提供的信息,给出下列说法:
①汽车共行驶了120千米;
②汽车在行驶途中停留了0.5小时;
③汽车在整个行驶过程中的平均速度为千米/时;
④汽车自出发后3小时至4.5小时之间行驶的速度在逐渐减少.
其中正确的说法有( )
A. 1个 B. 2个 C. 3个 D. 4个
二、填空题:(每题3分,共24分)
11. 的算术平方根是_________.
12. 把命题“对顶角相等”改写成“如果…那么…”的形式_________.
13. 在函数中,自变量的取值范围是_________.
14. 直角三角形的两条边长是4和5,则第三边长是_________.
15. 在平面直角坐标系中,已知点.点,且直线轴,求线段的长_________.
16. 已知,则的平方根为_________.
17. 如图,在直角坐标系中,设动点自处向上运动1个单位至,然后向左运动2个单位至处,再向下运动3个单位至处,再向右运动4个单位至处,再向上运动5个单位至处,……,如此继续运动下去,设,,则_________.
18. 如图,中,,,,若点、、分别是三边、、上的动点,则周长的最小值为_________.
三、解答题(本答题共10题,共66分)
19. 计算题(每题3分,共6分)
(1) (2)
20.(共6分)如图所示的方格纸中,每个小方格的边长都是1,点,,.
(1)作关于轴对称的;
(2)在轴上作出点,使最小,并直接写出点的坐标.
21.(共5分)如图,已知长方形中,,,在边上取一点,将折叠使点恰好落在边上的点,求的长?
22.(共6分)如图,直线经过点和点.
(1)求直线的函数表达式;
(2)求的面积.
23.(共6分)某校举办了国学知识竞赛,满分10分,学生得分均为整数.在初赛中,甲乙两组(每组10人)学生成绩如下(单位:分)
甲组:3,6,6,6,6,6,7,9,9,10
乙组:5,6,6,6,7,7,7,7,8,9
组别 平均数 中位数 众数 方差
甲组 6.8 6 3.76
乙组 7 1.16
(1)以上成绩统计分析表中_________,_________,_________.
(2)小明同学说:“这次竞赛我得了7分,在我们小组中属中游略偏上!”观察上面表格判断,小明可能是__________组的学生;
(3)从平均数和方差看,若从甲乙两组学生中选择一个组参加决赛,应选哪个组?并说明理由.
24.(共6分)甲、乙两车分别从两地同时出发,甲车匀速前往地,乙车匀速前往地,到达地立即以另一速度按原路匀速返回到地,设甲、乙两车离地的路程为(千米),乙车行驶的时间为(时),与之间的函数图象如图所示.
(1)乙车从地到达地的速度是__________千米/时;
(2)乙车到达地时甲车距地的路程是__________千米;
(3)_________;_________.
25.(共8分)如图,四边形中,,,点是的中点,连接,将沿折叠后得到,且点在四边形内部,延长交于点,连接.且.
(1)求证:;
(2)求证:;
(3)若点是的中点,,求的长.
26.(共8分)某景点的门票价格如下表:
购票人数(人) 1~50 51~99 100以上(含100)
门票单价(元) 48 45 42
(1)某校七年级1、2两个班共有102人去游览该景点,其中1班人数少于50人,2班人数多于50人且少于100人.如果两班都以班为单位单独购票,则一共支付4737元,两个班各有多少名学生?
(2)该校八、九年级自愿报名浏览该景点,其中八年级的报名人数不超过50人,九年级的报名人数超过50人,但不超过80人.若两个年级分别购票,总计支付门票费4914元;若合在一起作为一个团体购票,总计支付门票费4452元,问八年级、九年级各报名多少人?
27.(共7分)观察下列式子的变形过程,完成下列任务:
.
类比上述变形过程的基本思路,猜想的结果并验证.
计算:.
28.(共8分)如图,将一张边长为8的正方形纸片放在直角坐标系中,使得与轴重合,与轴重合,点为正方形边上的一点(不与点、点重合).将正方形纸片折叠,使点落在处,点落在处,交于,折痕为.连接、.
初步探究
(1)当时
①直接写出点的坐标;
②求直线的函数表达式.
深入探究
(2)当点在边上移动时,与的度数总是相等,请说明理由.
拓展应用
(3)当点在边上移动时,的周长是否发生变化?并证明你的结论.
龙凤区2021-2022学年第二学期期末考试七年级
数学考试题答案
一、选择题(每题3分共30分)
1 2 3 4 5 6 7 8 9 10
B D D B C C C B D B
二、填空题(每题3分共24分)
11 12 13 14
3 如果两个角是对顶角,那么它们相等 3或
15 16 17 18
3 50
19.计算(6分)
解:(3分)(1) (2)(3分)
20.(1)如图所示,即为所求;
----------3分
(2)作点关于轴的对称点,再连接交轴于点,其坐标为.------3分
21.(5分)∵四边形是矩形,
∴,,
根据题意得:,
∴,,,
设,则,
在中,由勾股定理得:,
即,
∴,
∴,
在中,由勾股定理可得:,
即,
∴,
∴,
即.
故答案为.-------5分
22.(1)设直线的函数表达式为,
因为直线经过点和点,
所以,
解得.
所以直线的函数表达式为.
(2)设直线与轴交于点,则,
所以
.
23.(1)6,-------1分
6.8,-------1分
7;-------1分
(2)甲;-------1分
(3)选乙组参加决赛.理由如下:
∵甲乙两组学生平均数相同,而,
∴乙组的成绩比较稳定,
故选乙组参加决赛.-------2分
24. 解:(1)由图象可得,
乙车从地到地的速度为:(千米/时),
故答案为:120;-------2分
(2)由图象可得,
,
甲车的速度为:(千米/时),
则乙车到达地时甲车距地的路程是(千米),
故答案为:100;-------2分
(3);-------2分
25. 解:(1)可由或证;-------3分
(2)折叠得到,
∴,
∵,,
∴,,
∴四边形为矩形,
∴,
∴;-------2分
(3)∵点是中点,,
∴,
∵点中点,
∴设,则,
则,即,
即,
且,即,
且,即,
∵,,
∴,
∴,
∴,
解得:,即.-------3分
26. 解:(1)设七年级1班有名学生,2班有y名学生,
由题意得:,
解得:,
答:七年级1班有49名学生,2班有53名学生;-------4分
(2)设八年级报名人,九年级报名人,
分两种情况:
①若,
由题意得:,
解得:,(不合题意舍去);
②若,
由题意得:,
解得:,符合题意;
答:八年级报名48人,九年级报名58人.-------4分
27.(1).验证:
;
(2)原式
.
28.(1)①设:,则,,
在中,由勾股定理得:,
即,解得:,
故点.
故答案为:;-------2分
②过点作轴于点,
折叠后点落在处,则点、关于直线对称,则,
∴,而,
∴,
而,,
∴,
∴,
,故点,
将点、的坐标代入一次函数表达式:,
得:,解得:,
故直线的表达式为:;-------2分
(2)∵,
∴.
又∵,
∴.
即.
又∵,
∴,
∴;-------2分
(3)如图,过作,垂足为.
由(1)知,
在和中,
,
∴,
∴,.
又∵,
∴.
又∵,,
∴,
∴,
∴的周长.
故答案为:16.-------2
同课章节目录
