1.1.2集合的基本关系 教案
文档属性
| 名称 | 1.1.2集合的基本关系 教案 |

|
|
| 格式 | doc | ||
| 文件大小 | 1.6MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教B版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-07-08 14:00:33 | ||
图片预览


文档简介
中小学教育资源及组卷应用平台
1.1集合
1.1.2集合的基本关系
(人教B版)
一、教学目标
1. 了解集合之间的基本关系.
2. 理解子集.真子集的概念.
3. 能使用图表达集合间的关系,培养直观逻辑思维。
二、重难点
重点:集合间的基本关系.
难点:属于关系与包含关系的区别.
三、教学过程
1、 问题导入:
问题1:如果一个班级中,所有同学组成的集合记为S,而所有女同学组成的集合记为F,你觉得集合S和F之间有怎样的关系?你能从集合元素的角度分析它们的关系吗?问题考2:给定集合A={1,3},B={1,3,5,6},容易看出,集合A的任意一个元素都是集合B的元素.
二、知识讲解
(一)知识整理
概念一 子集
(1)一般地,如果集合A中任意一个元素都是集合B中的元素,那么集合A称为集合B的子集.
记作:
读作:A包含于B(或B包含A).
(2)空集:不含有任何元素的集合称为空集,记作:.
任意集合A都是它自身的子集,即AA.
空集是任意一个集合A的子集,即A.
如果两个集合所含的元素完全相同(),那么我们称这两个集合相等.
记作:
读作:A等于B.
概念二 真子集
1、根据子集的定义,让学生用类比的思维写出真子集的定义。
2、接下来由教师给出维恩图(Venn图)的定义,并且用韦恩图分别表示子集、真子集。
子集:
集合相等:
真子集:
问题三 集合的相等与子集的关系
1.首先让同学们思考以下问题:已知S={x|(x+1)(x+2)=0},T={-1,-2},这两个集合的元素的关系,即ST吗?TS吗?
2.接下来同学们分小组讨论,并且总结出集合相等的定义与子集的关系。
定义:一般地,由集合相等以及子集的定义可知:
(1)如果AB且BA,则A=B;
(2)如果A=B,则AB且BA.
四、例题解析
例1例写出集合A={6,7,8}的所有子集和真子集.
解:集合A的所有子集是
,{6),{7},{8},{6,7},{6,8},{7,8},{6,7,8}.
在上述子集中,除去集合A本身,即{6,7,8},剩下的都是A的。
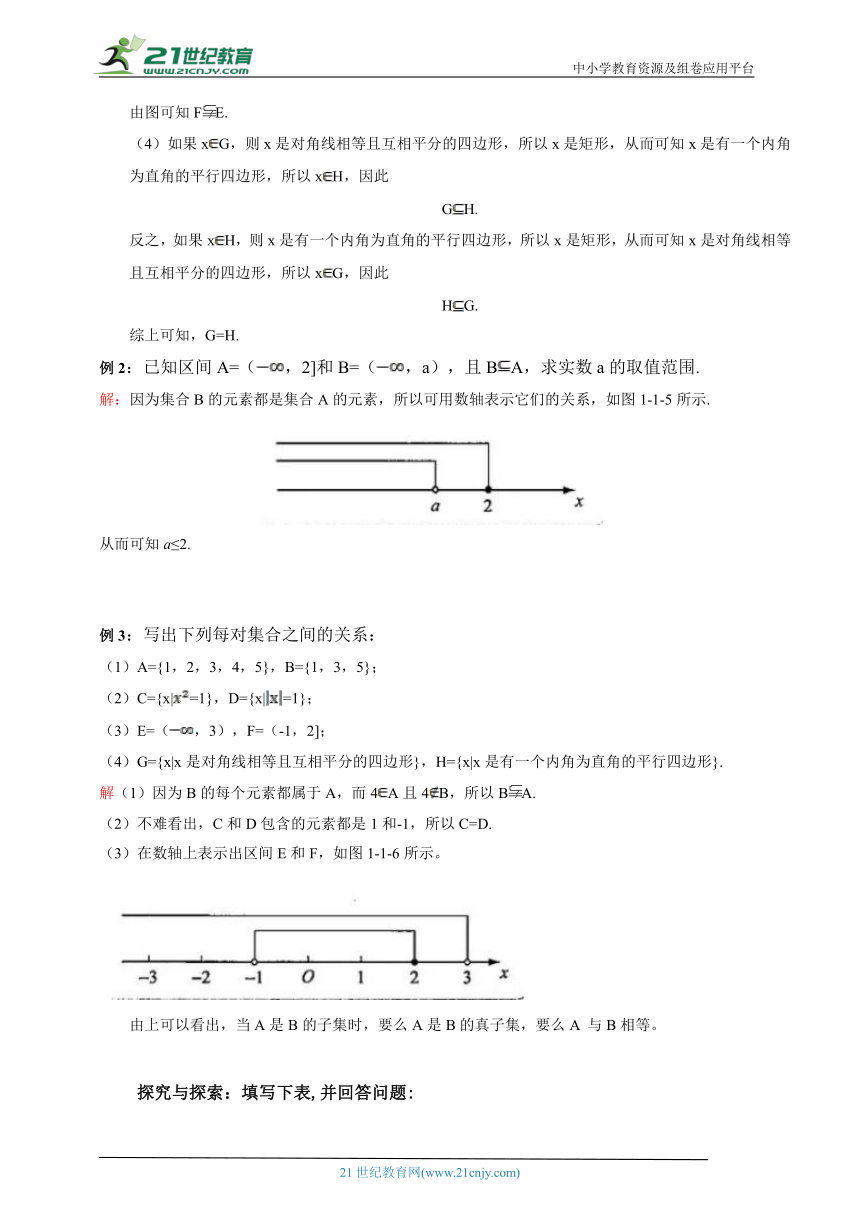
例2:已知区间A=(,2]和B=(,a),且BA,求实数a的取值范围.
解:因为集合B的元素都是集合A的元素,所以可用数轴表示它们的关系,如图1-1-5所示.
从而可知a≤2.
例3:写出下列每对集合之间的关系:
(1)A={1,2,3,4,5},B={1,3,5};
(2)C={x|=1},D={x|=1};
(3)E=(,3),F=(-1,2];
(4)G={x|x是对角线相等且互相平分的四边形},H={x|x是有一个内角为直角的平行四边形}.
解(1)因为B的每个元素都属于A,而4A且4B,所以BA.
(2)不难看出,C和D包含的元素都是1和-1,所以C=D.
(3)在数轴上表示出区间E和F,如图1-1-6所示。
由图可知FE.
(4)如果xG,则x是对角线相等且互相平分的四边形,所以x是矩形,从而可知x是有一个内角为直角的平行四边形,所以xH,因此
GH.
反之,如果xH,则x是有一个内角为直角的平行四边形,所以x是矩形,从而可知x是对角线相等且互相平分的四边形,所以xG,因此
HG.
综上可知,G=H.
由上可以看出,当A是B的子集时,要么A是B的真子集,要么A 与B相等。
探究与探索:填写下表,并回答问题:
由此猜想:含n个元素的集合{a1,a2,…,an}的所有子集的个数是多少 真子集的个数及非空真子集的个数呢
【答案】见解析
【解析】分析:由特殊到一般,归纳得出.
解:
五、课堂小结
让学生总结本节课所学主要知识及解题技巧
六、板书设计
七、作业
课本14页习题A
B
A
1.1 集合的概念
1.子集 例1 例2 例3
2.真子集
3.集合的相等与子集的关系
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世纪教育网(www.21cnjy.com)
1.1集合
1.1.2集合的基本关系
(人教B版)
一、教学目标
1. 了解集合之间的基本关系.
2. 理解子集.真子集的概念.
3. 能使用图表达集合间的关系,培养直观逻辑思维。
二、重难点
重点:集合间的基本关系.
难点:属于关系与包含关系的区别.
三、教学过程
1、 问题导入:
问题1:如果一个班级中,所有同学组成的集合记为S,而所有女同学组成的集合记为F,你觉得集合S和F之间有怎样的关系?你能从集合元素的角度分析它们的关系吗?问题考2:给定集合A={1,3},B={1,3,5,6},容易看出,集合A的任意一个元素都是集合B的元素.
二、知识讲解
(一)知识整理
概念一 子集
(1)一般地,如果集合A中任意一个元素都是集合B中的元素,那么集合A称为集合B的子集.
记作:
读作:A包含于B(或B包含A).
(2)空集:不含有任何元素的集合称为空集,记作:.
任意集合A都是它自身的子集,即AA.
空集是任意一个集合A的子集,即A.
如果两个集合所含的元素完全相同(),那么我们称这两个集合相等.
记作:
读作:A等于B.
概念二 真子集
1、根据子集的定义,让学生用类比的思维写出真子集的定义。
2、接下来由教师给出维恩图(Venn图)的定义,并且用韦恩图分别表示子集、真子集。
子集:
集合相等:
真子集:
问题三 集合的相等与子集的关系
1.首先让同学们思考以下问题:已知S={x|(x+1)(x+2)=0},T={-1,-2},这两个集合的元素的关系,即ST吗?TS吗?
2.接下来同学们分小组讨论,并且总结出集合相等的定义与子集的关系。
定义:一般地,由集合相等以及子集的定义可知:
(1)如果AB且BA,则A=B;
(2)如果A=B,则AB且BA.
四、例题解析
例1例写出集合A={6,7,8}的所有子集和真子集.
解:集合A的所有子集是
,{6),{7},{8},{6,7},{6,8},{7,8},{6,7,8}.
在上述子集中,除去集合A本身,即{6,7,8},剩下的都是A的。
例2:已知区间A=(,2]和B=(,a),且BA,求实数a的取值范围.
解:因为集合B的元素都是集合A的元素,所以可用数轴表示它们的关系,如图1-1-5所示.
从而可知a≤2.
例3:写出下列每对集合之间的关系:
(1)A={1,2,3,4,5},B={1,3,5};
(2)C={x|=1},D={x|=1};
(3)E=(,3),F=(-1,2];
(4)G={x|x是对角线相等且互相平分的四边形},H={x|x是有一个内角为直角的平行四边形}.
解(1)因为B的每个元素都属于A,而4A且4B,所以BA.
(2)不难看出,C和D包含的元素都是1和-1,所以C=D.
(3)在数轴上表示出区间E和F,如图1-1-6所示。
由图可知FE.
(4)如果xG,则x是对角线相等且互相平分的四边形,所以x是矩形,从而可知x是有一个内角为直角的平行四边形,所以xH,因此
GH.
反之,如果xH,则x是有一个内角为直角的平行四边形,所以x是矩形,从而可知x是对角线相等且互相平分的四边形,所以xG,因此
HG.
综上可知,G=H.
由上可以看出,当A是B的子集时,要么A是B的真子集,要么A 与B相等。
探究与探索:填写下表,并回答问题:
由此猜想:含n个元素的集合{a1,a2,…,an}的所有子集的个数是多少 真子集的个数及非空真子集的个数呢
【答案】见解析
【解析】分析:由特殊到一般,归纳得出.
解:
五、课堂小结
让学生总结本节课所学主要知识及解题技巧
六、板书设计
七、作业
课本14页习题A
B
A
1.1 集合的概念
1.子集 例1 例2 例3
2.真子集
3.集合的相等与子集的关系
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世纪教育网(www.21cnjy.com)
