滕一东校-高二不等式
图片预览



文档简介
复习课:不等式与不等关系
滕州一中东校 韩霞
教学目标
重点: 不等式性质的应用,一元二次不等式的解法,用二元一次不等式(组)表示平面区域,求线性目标函数在线性约束条件下的最优解,基本不等式的应用.
难点:利用不等式加法法则及乘法法则解题,求目标函数的最优解,基本不等式的应用。
知识点:1. 不等式性质的应用2.一元二次不等式的解法3.用二元一次不等式(组)表示平面区域,求线性目标函数在线性约束条件下的最优解4.基本不等式的应用.
能力点:1.温故本章内容,使知识系统化,条理化.分清重点,明确难点,再现注意点,达到巩固与知新的效果.2.体会分类讨论,等价转化,数形结合,函数方程四种数学思想的应用.通过阶梯性的强化练习,培养学生分析问题解决问题的能力。
教育点:1.提高学生的运算能力和逻辑思维能力.2.培养学生化归(或转化)的数学思想.3.培养学生分类讨论的数学思想. 4.进一步提高分析问题和解决问题的能力,提高学生的数学素质.
自主探究点:结合本章的知识网络结构,引导学习补充相关内容,同时强化学生对不等式基本性质、基本公式及定理的熟练掌握.结合典型的例(习)题,教师给予及时的启发或点拨,真正使学生解题能力得到锻炼和提高.
考试点:不等式性质的应用,一元二次不等式的解法,用二元一次不等式(组)表示平面区域,求线性目标函数在线性约束条件下的最优解,基本不等式的应用.
易错易混点:含有参数的不等式的解法以及恒成立问题.
拓展点:含有参数的不等式的解法以及恒成立问题
学法与教具
学法:讲练结合、启发诱导 2.教具:多媒体、三角板
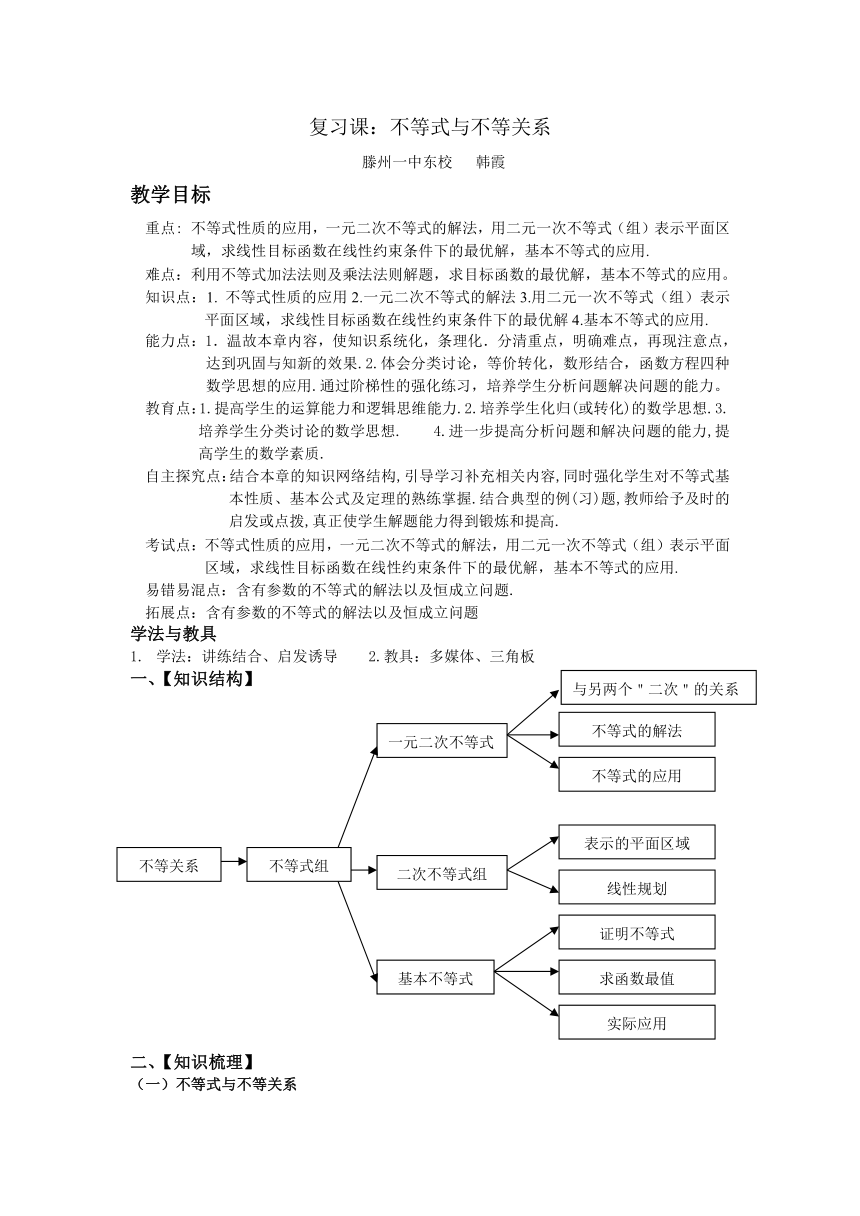
一、【知识结构】
二、【知识梳理】
(一)不等式与不等关系
1、应用不等式(组)表示不等关系;
不等式的主要性质:
(1)对称性:
(2)传递性:
(3)加法法则:;
(4)乘法法则:;
(5)倒数法则:
(6)乘方法则:
(7)开方法则:
2、应用不等式的性质比较两个实数的大小;
作差法
3、应用不等式性质证明
(二)一元二次不等式及其解法
1.一元二次不等式的解法
一元二次不等式的解集:
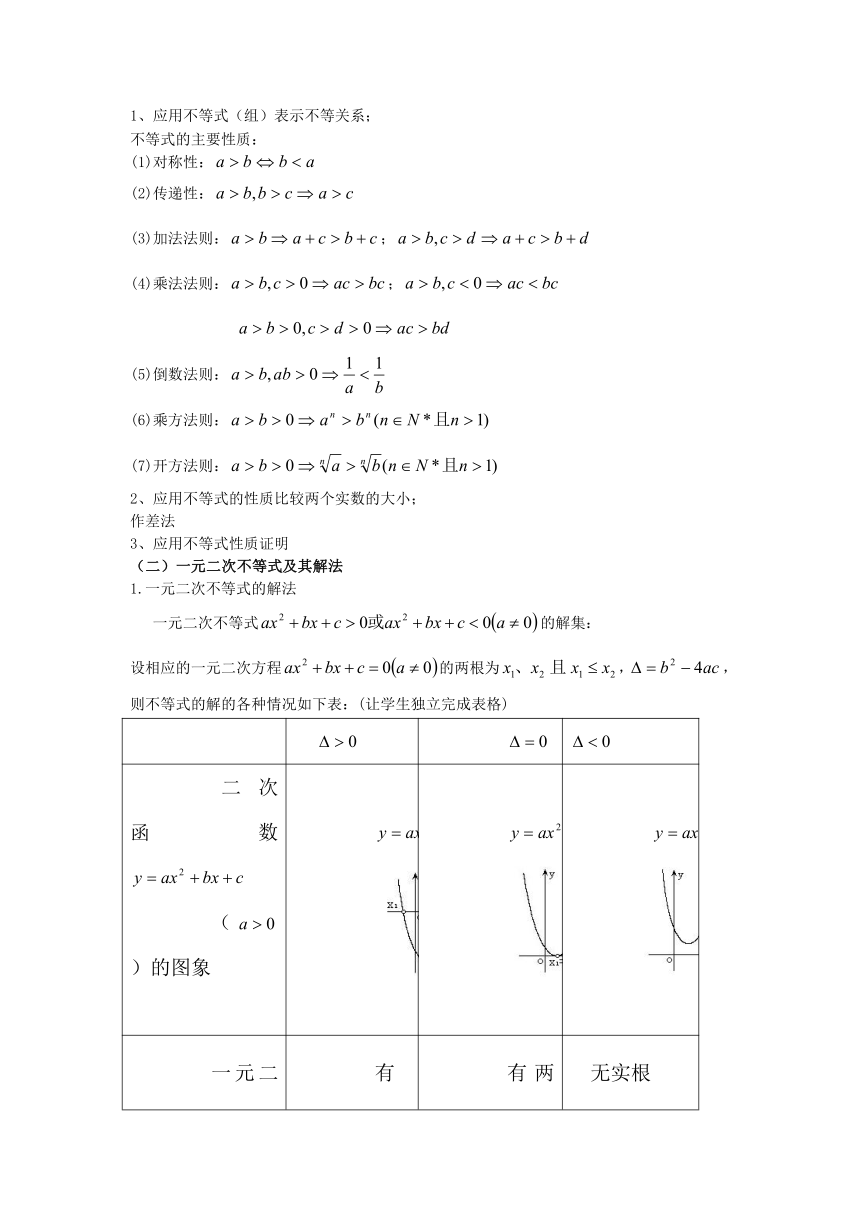
设相应的一元二次方程的两根为,,则不等式的解的各种情况如下表:(让学生独立完成表格)
二次函数()的图象
一元二次方程 有两相异实根 有两相等实根 无实根
R
2.一元二次不等式恒成立情况小结:
()恒成立.
()恒成立.
(三)线性规划
1、用二元一次不等式(组)表示平面区域
二元一次不等式Ax+By+C>0在平面直角坐标系中表示直线Ax+By+C=0某一侧所有点组成的平面区域.(虚线表示区域不包括边界直线)
2、二元一次不等式表示哪个平面区域的判断方法
法一:由于对在直线Ax+By+C=0同一侧的所有点(),把它的坐标()代入Ax+By+C,所得到实数的符号都相同,所以只需在此直线的某一侧取一特殊点(x0,y0),从Ax0+By0+C的正负即可判断Ax+By+C>0表示直线哪一侧的平面区域.(特殊地,当C≠0时,常把原点作为此特殊点)
法二:一般地,直线把平面分成两个区域:
表示直线上方的平面区域;表示直线下方的平面区域.
说明:(1)表示直线及直线上方的平面区域;
表示直线及直线下方的平面区域.
(2)对于不含边界的区域,要将边界画成虚线.
3、线性规划的有关概念:
①线性约束条件:在上述问题中,不等式组是一组变量x、y的约束条件,这组约束条件都是关于x、y的一次不等式,故又称线性约束条件.
②线性目标函数:
关于x、y的一次式z=2x+y是欲达到最大值或最小值所涉及的变量x、y的解析式,叫线性目标函数.
③线性规划问题:
一般地,求线性目标函数在线性约束条件下的最大值或最小值的问题,统称为线性规划问题.
④可行解、可行域和最优解:
满足线性约束条件的解(x,y)叫可行解.
由所有可行解组成的集合叫做可行域.
使目标函数取得最大或最小值的可行解叫线性规划问题的最优解.
4、求线性目标函数在线性约束条件下的最优解的步骤:
(1)寻找线性约束条件,线性目标函数;
(2)由二元一次不等式表示的平面区域做出可行域;
(3)在可行域内求目标函数的最优解
(四)基本不等式
1.如果,那么.
2.如果a,b是正数,那么
3.基本不等式几何意义是“半径不小于半弦”
三、【范例导航】
例1.解一元二次不等式
解下列不等式:
(1) ; (2) ;
(3) ; (4) .
【分析】观察不等式的形式,需要先考虑对应方程的判别式及方程的根,然后画出相应二次函数的图象帮助理解,最后根据图象写出不等式的解集,最终得到原不等式的解集.
【解答】(1)方程的解为.根据的图象,可得原不等式的解集是.
(2)不等式两边同乘以,原不等式可化为.
方程的解为.
根据的图象,可得原不等式的解集是.
(3)方程有两个相同的解.
根据的图象,可得原不等式的解集为.
(4)因为,所以方程无实数解,根据的图象,可得原不等式的解集为.
【点评】通过四种不同形式的题目,让学生从各个方面对一元二次不等式进行进一步了解,强调一些注意事项,让学生规范解答.解一元二次不等式的步骤:
(1)化标准:将不等式化成标准形式(右边为0、最高次的系数为正);
(2)判Δ,求根:计算判别式的值,若值为正,则求出相应方程的两根;
(3)下结论:注意结果要写成集合或者区间的形式.
解题步骤总结为:一化正→→二算Δ→→三求根→→四写解集
变式训练:求函数的定义域.
解:要使得函数有意义,则
所以, 即,
故函数的定义域是.
例2. 已知不等式的解集是{x|3【分析】解一元二次不等式时,只有当图像与x轴有2个交点时,才会出现x介于两者之间,且这两者就是一元二次不等式所对应的方程的根.故方程的两个根为3,4.
【解答】法一:(代入法)
方程的两个根为3,4,把3,4代入方程,可得:
,解得.
法二:(利用根与系数的关系)
方程的两个根为3,4,所以,
,解得
【点评】给出某个不等式的解集求参数的取值,训练学生的逆向思维能力,同时考察根与系数的关系(韦达定理),检验教学效果.
变式训练:已知不等式的解集为求不等式的解集.
解:由题意 , 即.
代入不等式得: .
即,所求不等式的解集为.
例3:解关于的不等式:
【解答】,
,
,
,
,
【点评】要重视分类讨论思想的培养,学习时,要学会分析引起分类讨论的原因,合理地分类,做到不重不漏.
变式训练:.
解:当或时,,当时,
当或时,.
例4.设,式中变量满足条件,求的最大值和最小值.
解:由题意,变量所满足的每个不等式都表示一个平面区域,不等式组则表示这些平面区域的公共区域.由图知,原点不在公共区域内,当时,,即点在直线:上,
作一组平行于的直线:,,
可知:当在的右上方时,直线上的点
满足,即,
而且,直线往右平移时,随之增大.
由图象可知,
当直线经过点时,对应的最大,
当直线经过点时,对应的最小,
所以,,.
变式训练:设,式中满足条件,求的最大值和最小值.
解:当与所在直线重合时最大,此时满足条件的最优解有无数多个,当经过点时,对应最小,
∴,.
例4、若,则为何值时有最小值,最小值为多少?
【分析】注意一正、二定、三相等
【解答】∵, ∴, ∴,∴=
,当且仅当即时.
变式训练:求(x>5)的最小值.
例5.若,求的最小值。
【解答】∵,∴
当且仅当,即时取等号,
∴当时,取最小值.
变式训练:已知正数x、y满足,则的最小值是( )
答案:18
例6.已知,如图,设矩形ABCD(AB>CD)的周长为24,把它关于AC折起来,AB折过去后,交CD于点P.设AB=x,求△ADP的最大面积及相应的x值.
【分析】要求△ADP的最大面积,首先要写出△ADP的面积表达式.由于AD=12-x,关键是将DP用x表示出来.从右图中看到,DP=PB′,AP=x-OP,于是在△ADP中运用勾股定理,可以将DP用x表示出来.
【解答】如图,∵AB=x,∴AD=12-x
又DP=PB′,
∴AP=AB′-PB′=AB-DP=x-DP
由勾股定理得:
(12-x)2+DP2=(x-DP)2,
整理得:DP=12-
因此△ADP的面积:
S△ADP=AD·DP
=(12-x)·(12-)
=108-(6x+)
又∵x>0,
∴6x+≥2=72.
∴S=108-(6x+)≤108-72.
当且仅当6x=时,即当x=6时,S有最大值108-72.
答:当x=6时,△ADP的面积有最大值108-72.
【点评】此题考查综合应用所学数学知识,思想和方法解决实际问题的能力,考查函数关系、不等式性质、最大值、最小值等基础知识,考查利用均值不等式求最值的方法.
变式训练:某食品厂定期购买面粉,已知该厂每天需要面粉6吨,每吨面粉的价格为1800元,面粉的保管等其它费用为平均每吨每天3元,购面粉每次需支付运费900元.求该厂多少天购买一次面粉,才能使平均每天所支付的总费用最少?
解:设该厂天购买一次面粉,平均每天所支付的总费用为元.
∴购买面粉的费用为元,
保管等其它费用为,
∴
当,即时,有最小值,
答:该厂天购买一次面粉,才能使平均每天所支付的总费用最少.
四、【解法小结】
1.二次函数、一元二次方程和一元二次不等式是一个有机的整体,要深刻理解它们之间的相互关系,会用函数思想来研究方程和不等式.
2.二元一次不等式(组)表示平面区域与线性规划问题是数形结合思想的运用。画平面区域是线性规划的基础,常用选点法定侧,注意边界是否在区域内。解线性规划应用题时要注意规范解题,写全解题步骤。
解线性规划应用题的一般步骤:①设出未知数;②列出约束条件;③建立目标函数;④求最优解;
3.利用基本不等式求最值或证明不等式,运用时往往需作适当的变形,创造条件应用基本不等式,常用变换技巧是“拆添项”“配凑因子”和“平方”等。应用基本不等式求最值时,要注意考虑三要素,即“一正二定三相等”.
五、【布置作业】
必做题:
1.已知a,b,c∈R,下列命题中正确的是
A、 B、
C、 D、
2.已知不等式的解集为,则不等式的解集为
A、 B、
C、 D、 ( )
3.不等式组的解集为 .
5.已知,,则的最小值为 .
5. 不等式的解集是_________ .()
10.已知x>2,则y=的最小值是 4 .
15.已知x、y满足不等式,求z=3x+y的最大值与最小值。
15.
必做题答案:B B(1,2)∪(4,5) 15
1.如果,那么,下列不等式中正确的是( A )
(A) (B) (C) (D)
3. 若,则下列不等式成立的是( C )
(A) . (B). (C).(D).
6.已知实数满足,则的最大值是_________.(KEY:0).
选做题:1.二次方程,有一个根比大,另一个根比小,则的取值范围是(C )
A. B. C. D.
11.对于任意实数x,不等式恒成立,则实数k的取值范围是
12、设满足且则的最大值是 。11.,12.2,
某工厂生产A,B两种产品,已知生产1千克A产品要用煤9吨,电力4千瓦时,劳动力3个,创造利润7万元,生产1千克B产品要用煤4吨,电力5千瓦时,劳动力10个,创造利润12万元,在这种条件下,应该生产A,B两种产品各多少千克,才能使所创造的总的经济价值最高?
答案:容易解得当x=20,y=24时,目标函数z=7x+12y取得最大值428万元。
六、【教后反思】
1.本教案的亮点是:首先以结构图呈现角函数的概念和三角函数的概念,直观简明;其次,复习相关知识并以表格的形式呈现,充分关注到自然语言、符号语言、图形语言三种语言之间的互译问题.再次,例题选择典型,关注三角的主干知识和解决三角问题的一般思路与方法,讲练结合,学生落实较好.最后,在作业的布置上,选择高考中的低档题,对学生理解、巩固知识能够起到良好的作用.
2.本教案的弱项:在一些具体问题中,学生容易忽略角的范围的讨论,容易漏解.在例题2的设计上,可以稍微增加专项练习.
在不等式的证明中,加强化归(或转化)思想的学习,证不等式的过程是一个把已知条件向要证结论的一个转化过程.
在学习时应加强应用意识,总结不等式的应用规律,才能提高解决问题的能力.如在实际问题中,主要有构造不等式求解或构造函数求函数的最值等方法,求最值时要注意等号成立的条件.
结合本章的知识网络结构,引导学习补充相关内容,同时强化学生对不等式基本性质、基本公式及定理的熟练掌握.结合典型的例(习)题,教师给予及时的启发或点拨,真正使学生解题能力得到锻炼和提高. 不等式既是中学数学的重要内容,又是学习高等数学的基础和工具.它具有广泛应用、变换灵活等特点,是历年高考命题的热点.从题型上看,在客观题中主要考查不等式的性质,比较数的大小、解简单的不等式;在解答题中解不等式往往需要对所含参数进行讨论;应用问题往往将不等式与函数及其性质,方程解法的讨论,两曲线位置关系的讨论等问题加以综合;推理论证问题往往与不等式的证明相关联,构成代数的压轴题.在本章中,学生通过具体情境感受不等关系,理解不等式(组)对于刻画不等关系的意义和价值;掌握求解一元二次不等式的基本方法,并能解决一些实际问题;能用二元一次不等式组表示平面区域,并尝试解决一些简单的二元线性规划问题;认识基本不等式及其简单应用;体会不等式、方程及函数之间的联系.我们将重点研究一元二次不等式、二元一次不等式(组)、基本不等式三种不等式模型,在了解不等式实际背景的前提下,重点研究不等式的应用.
与另两个"二次"的关系
不等式的解法
一元二次不等式
不等式的应用
表示的平面区域
二次不等式组
不等式组
不等关系
线性规划
证明不等式
求函数最值
基本不等式
实际应用
滕州一中东校 韩霞
教学目标
重点: 不等式性质的应用,一元二次不等式的解法,用二元一次不等式(组)表示平面区域,求线性目标函数在线性约束条件下的最优解,基本不等式的应用.
难点:利用不等式加法法则及乘法法则解题,求目标函数的最优解,基本不等式的应用。
知识点:1. 不等式性质的应用2.一元二次不等式的解法3.用二元一次不等式(组)表示平面区域,求线性目标函数在线性约束条件下的最优解4.基本不等式的应用.
能力点:1.温故本章内容,使知识系统化,条理化.分清重点,明确难点,再现注意点,达到巩固与知新的效果.2.体会分类讨论,等价转化,数形结合,函数方程四种数学思想的应用.通过阶梯性的强化练习,培养学生分析问题解决问题的能力。
教育点:1.提高学生的运算能力和逻辑思维能力.2.培养学生化归(或转化)的数学思想.3.培养学生分类讨论的数学思想. 4.进一步提高分析问题和解决问题的能力,提高学生的数学素质.
自主探究点:结合本章的知识网络结构,引导学习补充相关内容,同时强化学生对不等式基本性质、基本公式及定理的熟练掌握.结合典型的例(习)题,教师给予及时的启发或点拨,真正使学生解题能力得到锻炼和提高.
考试点:不等式性质的应用,一元二次不等式的解法,用二元一次不等式(组)表示平面区域,求线性目标函数在线性约束条件下的最优解,基本不等式的应用.
易错易混点:含有参数的不等式的解法以及恒成立问题.
拓展点:含有参数的不等式的解法以及恒成立问题
学法与教具
学法:讲练结合、启发诱导 2.教具:多媒体、三角板
一、【知识结构】
二、【知识梳理】
(一)不等式与不等关系
1、应用不等式(组)表示不等关系;
不等式的主要性质:
(1)对称性:
(2)传递性:
(3)加法法则:;
(4)乘法法则:;
(5)倒数法则:
(6)乘方法则:
(7)开方法则:
2、应用不等式的性质比较两个实数的大小;
作差法
3、应用不等式性质证明
(二)一元二次不等式及其解法
1.一元二次不等式的解法
一元二次不等式的解集:
设相应的一元二次方程的两根为,,则不等式的解的各种情况如下表:(让学生独立完成表格)
二次函数()的图象
一元二次方程 有两相异实根 有两相等实根 无实根
R
2.一元二次不等式恒成立情况小结:
()恒成立.
()恒成立.
(三)线性规划
1、用二元一次不等式(组)表示平面区域
二元一次不等式Ax+By+C>0在平面直角坐标系中表示直线Ax+By+C=0某一侧所有点组成的平面区域.(虚线表示区域不包括边界直线)
2、二元一次不等式表示哪个平面区域的判断方法
法一:由于对在直线Ax+By+C=0同一侧的所有点(),把它的坐标()代入Ax+By+C,所得到实数的符号都相同,所以只需在此直线的某一侧取一特殊点(x0,y0),从Ax0+By0+C的正负即可判断Ax+By+C>0表示直线哪一侧的平面区域.(特殊地,当C≠0时,常把原点作为此特殊点)
法二:一般地,直线把平面分成两个区域:
表示直线上方的平面区域;表示直线下方的平面区域.
说明:(1)表示直线及直线上方的平面区域;
表示直线及直线下方的平面区域.
(2)对于不含边界的区域,要将边界画成虚线.
3、线性规划的有关概念:
①线性约束条件:在上述问题中,不等式组是一组变量x、y的约束条件,这组约束条件都是关于x、y的一次不等式,故又称线性约束条件.
②线性目标函数:
关于x、y的一次式z=2x+y是欲达到最大值或最小值所涉及的变量x、y的解析式,叫线性目标函数.
③线性规划问题:
一般地,求线性目标函数在线性约束条件下的最大值或最小值的问题,统称为线性规划问题.
④可行解、可行域和最优解:
满足线性约束条件的解(x,y)叫可行解.
由所有可行解组成的集合叫做可行域.
使目标函数取得最大或最小值的可行解叫线性规划问题的最优解.
4、求线性目标函数在线性约束条件下的最优解的步骤:
(1)寻找线性约束条件,线性目标函数;
(2)由二元一次不等式表示的平面区域做出可行域;
(3)在可行域内求目标函数的最优解
(四)基本不等式
1.如果,那么.
2.如果a,b是正数,那么
3.基本不等式几何意义是“半径不小于半弦”
三、【范例导航】
例1.解一元二次不等式
解下列不等式:
(1) ; (2) ;
(3) ; (4) .
【分析】观察不等式的形式,需要先考虑对应方程的判别式及方程的根,然后画出相应二次函数的图象帮助理解,最后根据图象写出不等式的解集,最终得到原不等式的解集.
【解答】(1)方程的解为.根据的图象,可得原不等式的解集是.
(2)不等式两边同乘以,原不等式可化为.
方程的解为.
根据的图象,可得原不等式的解集是.
(3)方程有两个相同的解.
根据的图象,可得原不等式的解集为.
(4)因为,所以方程无实数解,根据的图象,可得原不等式的解集为.
【点评】通过四种不同形式的题目,让学生从各个方面对一元二次不等式进行进一步了解,强调一些注意事项,让学生规范解答.解一元二次不等式的步骤:
(1)化标准:将不等式化成标准形式(右边为0、最高次的系数为正);
(2)判Δ,求根:计算判别式的值,若值为正,则求出相应方程的两根;
(3)下结论:注意结果要写成集合或者区间的形式.
解题步骤总结为:一化正→→二算Δ→→三求根→→四写解集
变式训练:求函数的定义域.
解:要使得函数有意义,则
所以, 即,
故函数的定义域是.
例2. 已知不等式的解集是{x|3
【解答】法一:(代入法)
方程的两个根为3,4,把3,4代入方程,可得:
,解得.
法二:(利用根与系数的关系)
方程的两个根为3,4,所以,
,解得
【点评】给出某个不等式的解集求参数的取值,训练学生的逆向思维能力,同时考察根与系数的关系(韦达定理),检验教学效果.
变式训练:已知不等式的解集为求不等式的解集.
解:由题意 , 即.
代入不等式得: .
即,所求不等式的解集为.
例3:解关于的不等式:
【解答】,
,
,
,
,
【点评】要重视分类讨论思想的培养,学习时,要学会分析引起分类讨论的原因,合理地分类,做到不重不漏.
变式训练:.
解:当或时,,当时,
当或时,.
例4.设,式中变量满足条件,求的最大值和最小值.
解:由题意,变量所满足的每个不等式都表示一个平面区域,不等式组则表示这些平面区域的公共区域.由图知,原点不在公共区域内,当时,,即点在直线:上,
作一组平行于的直线:,,
可知:当在的右上方时,直线上的点
满足,即,
而且,直线往右平移时,随之增大.
由图象可知,
当直线经过点时,对应的最大,
当直线经过点时,对应的最小,
所以,,.
变式训练:设,式中满足条件,求的最大值和最小值.
解:当与所在直线重合时最大,此时满足条件的最优解有无数多个,当经过点时,对应最小,
∴,.
例4、若,则为何值时有最小值,最小值为多少?
【分析】注意一正、二定、三相等
【解答】∵, ∴, ∴,∴=
,当且仅当即时.
变式训练:求(x>5)的最小值.
例5.若,求的最小值。
【解答】∵,∴
当且仅当,即时取等号,
∴当时,取最小值.
变式训练:已知正数x、y满足,则的最小值是( )
答案:18
例6.已知,如图,设矩形ABCD(AB>CD)的周长为24,把它关于AC折起来,AB折过去后,交CD于点P.设AB=x,求△ADP的最大面积及相应的x值.
【分析】要求△ADP的最大面积,首先要写出△ADP的面积表达式.由于AD=12-x,关键是将DP用x表示出来.从右图中看到,DP=PB′,AP=x-OP,于是在△ADP中运用勾股定理,可以将DP用x表示出来.
【解答】如图,∵AB=x,∴AD=12-x
又DP=PB′,
∴AP=AB′-PB′=AB-DP=x-DP
由勾股定理得:
(12-x)2+DP2=(x-DP)2,
整理得:DP=12-
因此△ADP的面积:
S△ADP=AD·DP
=(12-x)·(12-)
=108-(6x+)
又∵x>0,
∴6x+≥2=72.
∴S=108-(6x+)≤108-72.
当且仅当6x=时,即当x=6时,S有最大值108-72.
答:当x=6时,△ADP的面积有最大值108-72.
【点评】此题考查综合应用所学数学知识,思想和方法解决实际问题的能力,考查函数关系、不等式性质、最大值、最小值等基础知识,考查利用均值不等式求最值的方法.
变式训练:某食品厂定期购买面粉,已知该厂每天需要面粉6吨,每吨面粉的价格为1800元,面粉的保管等其它费用为平均每吨每天3元,购面粉每次需支付运费900元.求该厂多少天购买一次面粉,才能使平均每天所支付的总费用最少?
解:设该厂天购买一次面粉,平均每天所支付的总费用为元.
∴购买面粉的费用为元,
保管等其它费用为,
∴
当,即时,有最小值,
答:该厂天购买一次面粉,才能使平均每天所支付的总费用最少.
四、【解法小结】
1.二次函数、一元二次方程和一元二次不等式是一个有机的整体,要深刻理解它们之间的相互关系,会用函数思想来研究方程和不等式.
2.二元一次不等式(组)表示平面区域与线性规划问题是数形结合思想的运用。画平面区域是线性规划的基础,常用选点法定侧,注意边界是否在区域内。解线性规划应用题时要注意规范解题,写全解题步骤。
解线性规划应用题的一般步骤:①设出未知数;②列出约束条件;③建立目标函数;④求最优解;
3.利用基本不等式求最值或证明不等式,运用时往往需作适当的变形,创造条件应用基本不等式,常用变换技巧是“拆添项”“配凑因子”和“平方”等。应用基本不等式求最值时,要注意考虑三要素,即“一正二定三相等”.
五、【布置作业】
必做题:
1.已知a,b,c∈R,下列命题中正确的是
A、 B、
C、 D、
2.已知不等式的解集为,则不等式的解集为
A、 B、
C、 D、 ( )
3.不等式组的解集为 .
5.已知,,则的最小值为 .
5. 不等式的解集是_________ .()
10.已知x>2,则y=的最小值是 4 .
15.已知x、y满足不等式,求z=3x+y的最大值与最小值。
15.
必做题答案:B B(1,2)∪(4,5) 15
1.如果,那么,下列不等式中正确的是( A )
(A) (B) (C) (D)
3. 若,则下列不等式成立的是( C )
(A) . (B). (C).(D).
6.已知实数满足,则的最大值是_________.(KEY:0).
选做题:1.二次方程,有一个根比大,另一个根比小,则的取值范围是(C )
A. B. C. D.
11.对于任意实数x,不等式恒成立,则实数k的取值范围是
12、设满足且则的最大值是 。11.,12.2,
某工厂生产A,B两种产品,已知生产1千克A产品要用煤9吨,电力4千瓦时,劳动力3个,创造利润7万元,生产1千克B产品要用煤4吨,电力5千瓦时,劳动力10个,创造利润12万元,在这种条件下,应该生产A,B两种产品各多少千克,才能使所创造的总的经济价值最高?
答案:容易解得当x=20,y=24时,目标函数z=7x+12y取得最大值428万元。
六、【教后反思】
1.本教案的亮点是:首先以结构图呈现角函数的概念和三角函数的概念,直观简明;其次,复习相关知识并以表格的形式呈现,充分关注到自然语言、符号语言、图形语言三种语言之间的互译问题.再次,例题选择典型,关注三角的主干知识和解决三角问题的一般思路与方法,讲练结合,学生落实较好.最后,在作业的布置上,选择高考中的低档题,对学生理解、巩固知识能够起到良好的作用.
2.本教案的弱项:在一些具体问题中,学生容易忽略角的范围的讨论,容易漏解.在例题2的设计上,可以稍微增加专项练习.
在不等式的证明中,加强化归(或转化)思想的学习,证不等式的过程是一个把已知条件向要证结论的一个转化过程.
在学习时应加强应用意识,总结不等式的应用规律,才能提高解决问题的能力.如在实际问题中,主要有构造不等式求解或构造函数求函数的最值等方法,求最值时要注意等号成立的条件.
结合本章的知识网络结构,引导学习补充相关内容,同时强化学生对不等式基本性质、基本公式及定理的熟练掌握.结合典型的例(习)题,教师给予及时的启发或点拨,真正使学生解题能力得到锻炼和提高. 不等式既是中学数学的重要内容,又是学习高等数学的基础和工具.它具有广泛应用、变换灵活等特点,是历年高考命题的热点.从题型上看,在客观题中主要考查不等式的性质,比较数的大小、解简单的不等式;在解答题中解不等式往往需要对所含参数进行讨论;应用问题往往将不等式与函数及其性质,方程解法的讨论,两曲线位置关系的讨论等问题加以综合;推理论证问题往往与不等式的证明相关联,构成代数的压轴题.在本章中,学生通过具体情境感受不等关系,理解不等式(组)对于刻画不等关系的意义和价值;掌握求解一元二次不等式的基本方法,并能解决一些实际问题;能用二元一次不等式组表示平面区域,并尝试解决一些简单的二元线性规划问题;认识基本不等式及其简单应用;体会不等式、方程及函数之间的联系.我们将重点研究一元二次不等式、二元一次不等式(组)、基本不等式三种不等式模型,在了解不等式实际背景的前提下,重点研究不等式的应用.
与另两个"二次"的关系
不等式的解法
一元二次不等式
不等式的应用
表示的平面区域
二次不等式组
不等式组
不等关系
线性规划
证明不等式
求函数最值
基本不等式
实际应用
