滕一东校-高二-常用逻辑用语复习课
文档属性
| 名称 | 滕一东校-高二-常用逻辑用语复习课 |  | |
| 格式 | zip | ||
| 文件大小 | 146.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2013-06-29 08:10:19 | ||
图片预览



文档简介
复习课: 常用逻辑用语
滕州一中东校 韩霞
教学目标
重点:充要条件的判断、四种命题的关系及等价性,命题真假的判断.
难点:对一些命题真假的判断.
知识点:1.了解命题及其逆命题、否命题与逆否命题,会分析四种命题的相互关系;2.理解必要条件、充分条件与充要条件的意义; 3.了解逻辑联结词‘‘或’’‘‘且’’‘‘非’’的含义;4.理解全称量词与存在量词的意义,能正确地对含有一个量词的命题进行否定.
能力点:1.温故本章内容,使知识系统化,条理化,达到巩固与知新的效果.2.体会分类讨论,等价转化,数形结合的数学思想的应用.3.通过强化练习,培养学生分析问题解决问题的能力.
教育点:1.提高学生的逻辑思维能力;2.培养学生化归(或转化)的数学思想,分类讨论的数学思想;3.进一步提高学生的认知水平,培养学生自己解决问题的能力,为学生塑造良好的数学认识结构.
自主探究点:例题及变式的解题思路的探索.
考试点:对命题真假的判断、复合命题的构成、命题的四种形式、充要条件与必要条件的判断、全称量词与存在量词的应用.
易错易混点:充分条件与必要条件判断.
拓展点:求参数的取值范围问题.
学法与教具
学法:讲练结合、启发诱导 2.教具:多媒体、学案
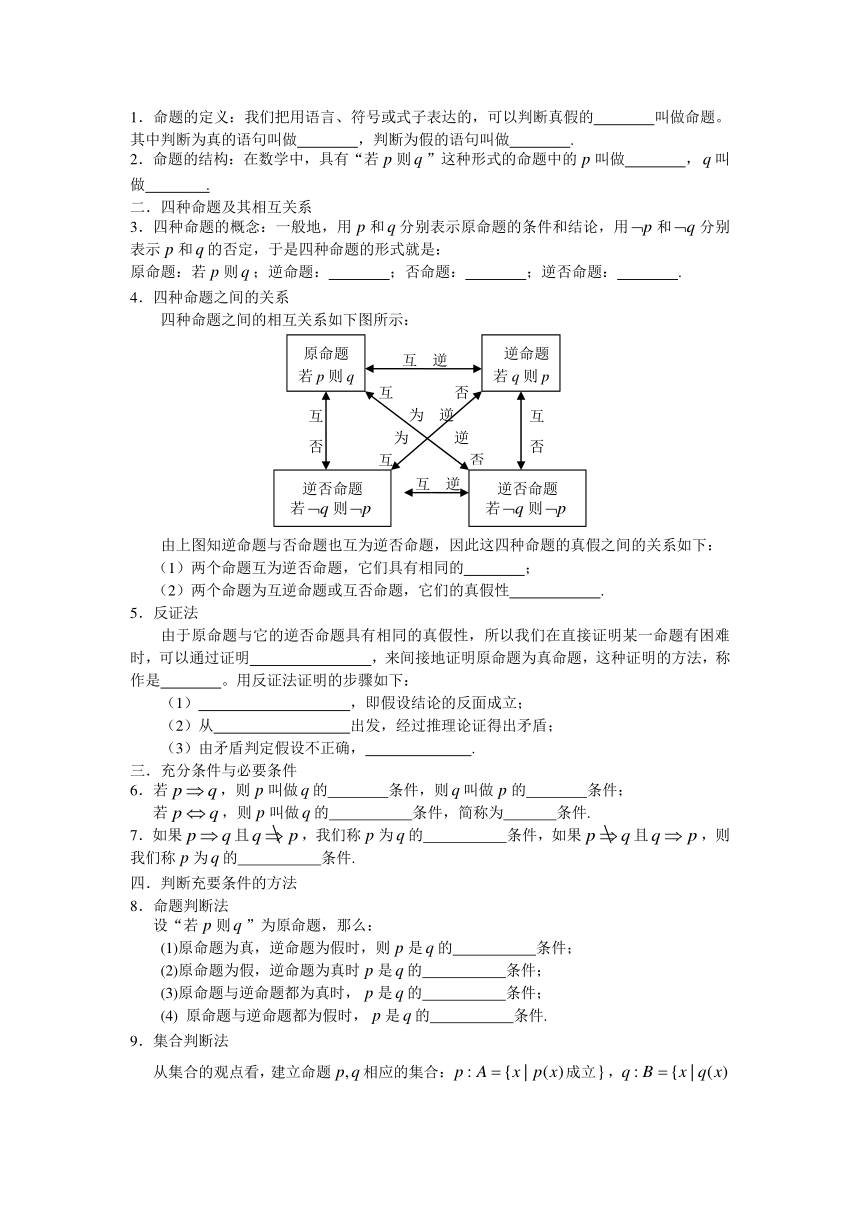
一、【知识结构】
二、【知识梳理】
一.命题
1.命题的定义:我们把用语言、符号或式子表达的,可以判断真假的 叫做命题。其中判断为真的语句叫做 ,判断为假的语句叫做 .
2.命题的结构:在数学中,具有“若则”这种形式的命题中的叫做 ,叫做 .
二.四种命题及其相互关系
3.四种命题的概念:一般地,用和分别表示原命题的条件和结论,用和分别表示和的否定,于是四种命题的形式就是:
原命题:若则;逆命题: ;否命题: ;逆否命题: .
4.四种命题之间的关系
四种命题之间的相互关系如下图所示:
由上图知逆命题与否命题也互为逆否命题,因此这四种命题的真假之间的关系如下:
(1)两个命题互为逆否命题,它们具有相同的 ;
(2)两个命题为互逆命题或互否命题,它们的真假性 .
5.反证法
由于原命题与它的逆否命题具有相同的真假性,所以我们在直接证明某一命题有困难时,可以通过证明 ,来间接地证明原命题为真命题,这种证明的方法,称作是 。用反证法证明的步骤如下:
(1) ,即假设结论的反面成立;
(2)从 出发,经过推理论证得出矛盾;
(3)由矛盾判定假设不正确, .
三.充分条件与必要条件
6.若,则叫做的 条件,则叫做的 条件;
若,则叫做的 条件,简称为 条件.
7.如果且,我们称为的 条件,如果且,则我们称为的 条件.
四.判断充要条件的方法
8.命题判断法
设“若则”为原命题,那么:
(1)原命题为真,逆命题为假时,则是的 条件;
(2)原命题为假,逆命题为真时是的 条件;
(3)原命题与逆命题都为真时,是的 条件;
(4) 原命题与逆命题都为假时,是的 条件.
9.集合判断法
从集合的观点看,建立命题相应的集合:成立,成立,那么:
(1)若,则是的 条件,若时,则是的 条件;
(2) 若,则是的 条件,若时,则是的 条件;
(3)若,则是的 条件,若且时,则是的 条件.
五.逻辑联结词
10.逻辑联结词:在数学中,有时会使用一些联结词,如 .
11.“且”记作 ;“或”记作 ;“非”记作 .
12.命题,和的真假判断
(1)当都是真命题时,为 ;为 ;为 .
(2)当有一个是真命题时,为 ;为 .
(3) 当都是假命题时,为 ;为 ;为 .
上述语句可以描述为:对于“一假必假”;对于“一真必真”;对于“真假相反”。
可以用下表来判断:(即真值表)
真 真
真 假
假 真
假 假
六.全称量词与存在量词
13.全称量词:短语 、 在逻辑中通常叫做全称量词,用符号 来表示;
含有全称量词的命题,叫做 .
全称命题“对中任意一个,有成立”可用符号简记为 .
14.存在量词:短语 、 在逻辑中通常叫做存在量词,用符号 来表示;
含有存在量词的命题,叫做 .
存在命题“存在中一个,使成立” 可用符号简记为 .
15.含有一个量词的命题的否定:
全称命题:,它的否定: ;即全称命题的否定是 .
特称命题:,它的否定: ;即全称命题的否定是 .
三、【范例导航】
1.四种命题的关系
例1写出下列命题的逆命题、否命题、逆否命题,并判断它们的真假.
(1)已知,,为实数,若,则有两个不相等的实数根;
(2)若或,则;
(3)若,则,全为零.
【分析】由定义写出其逆命题、否命题、逆否命题,然后判断其真假;也可利用命题间的等价性来判断.
【解答】(1)原命题是真命题;
逆命题:若有两个不相等的实数根,则,(假);
否命题:若,则没有两个不相等的实数根,(假);
逆否命题:若没有两个不相等的实数根,则,(真).
(2)原命题是真命题;
逆命题:若,则或,是真命题;
否命题:若且,则,是真命题;
逆否命题:若,则且,是真命题.
(3)原命题是真命题;
逆命题:若,全为零,则,(真);
否命题:若,则,不全为零,(真);
逆否命题:若,不全为零,则,(真).
【点评】(1)要注意四种命题之间的等价关系,即原命题与逆否命题等价,否命题与逆命题等价.判断一个命题是真命题时,要按照数学逻辑进行推理证明,而要说明它是假命题时,只需要举出一个反例即可.
(2)在否定条件或结论时,要注意否定词语的使用.常见否定词语有:
正面词语 等于(=) 大于(>) 小于(<) 有 是 都是 全是
否定词语 不等于() 不大于() 不小于() 无 不是 不都是 不全是
正面词语 任意的 任意两个 至少有一个 至多有一个 所有的 至多有个 或
否定词语 某个 某两个 一个也没有 至少有两个 某些 至少有个 且
变式训练:
写出下列命题的否命题,并判断真假
(1)若xy=0,则x,y中至少有一个为0;
(2)若x + y =0,则x,y中至多有一个大于0.
答案:(1)否命题:若,则x,y都不为0;(真)(2)否命题:若,则x,y都大于0(假)
2.充分必要条件
例2(1) “”是“”的( )
A.充分不必要条件 B.必要不充分条件 C.充要条件 D.既不充分也不必要条件
【分析】充要条件的判断前提是先明确条件与结论,即弄清楚哪个是条件,哪个是结论,再根据条件分析出推式的关系,从而利用定义和推式得到结论.
【解答】当时,,即.
反之,当时,有,
或,即.
综上所述,“”是“”的充分不必要条件,故选A.
(2)设集合,,那么“”是“”的( )
A.充分不必要条件 B.必要不充分条件 C.充要条件 D.既不充分也不必要条件
【分析】本题条件与结论的形式都是集合形式,只要理清集合之间的关系,按照充要条件与集合的对应关系即可作出判断.
【解答】∵,∴.故选A.
【点评】在从条件推结论,结论推条件时,可以利用学过的定理、定义和公式直接做逻辑判断,或利用数轴或Venn图分析两个集合的关系判断出“”和“”的真假.
例3已知是的充分条件而不必要条件,是的充分条件,是的必要条件,是的必要条件.现有下列命题:①是的充要条件;②是的充分而不必要条件;③是的必要而不充分条件;④的必要而不充分条件;⑤是的充分而不必要条件,则正确命题序号是( )
A.①④⑤ B.①②④ C.②③⑤ D.②④⑤
【分析】本题命题及其关系较多,如果直接解决则比较麻烦,可以用符号“”、“”等符号表示,简化题意,解决方便.
【解答】由题意可知:,且,.
所以,①正确;,且,②正确;,③不正确;
,且,④正确;,⑤不正确.故选B.
【点评】(1)本题考查了充分条件、必要条件、充要条件的概念及命题之间关系的转化,逆否命题的等价性,考查了逻辑思辩能力和转化思想.
(2)在命题之间的充分条件、必要条件、充要条件的推导过程中,使用符号语言可以简化过程,降低思维量.
变式训练:
已知命题:,命题:,若¬是¬的充分不必要条件,求实数的取值范围.
答案:.
3. 命题真假的判断
例4(1)已知命题:所有有理数都是实数,命题:正数的对数都是负数,则下列命题中为真命题的是
A. B. C. D.
【分析】本题只需要判断出命题和命题的真假,根据真值表进行判断即可.
【解答】由题意可以判断命题是真命题,命题是假命题,所以命题是假命题,命题是真命题.只有是真命题,故选D.
【点评】命题的真假判断是“一真必真”;命题的真假判断是“一假必假”;命题与的真假相反.
变式训练:
有四个关于三角函数的命题:
:, :、,
:, :
其中是假命题的有( )
A., B., C., D.,
答案:A.
4.命题的否定
例5已知命题:,则( )
A. B.C. D.
【分析】对全称(特称)命题的否定是将其全称(存在)量词改为存在(全称)量词,再将结论否定.
【解答】将变为,同时否定,可以得到,故选C.
【点评】一般地,对于含有一个量词的全称命题的否定,有下面的结论:
全称命题:,它的否定¬:,¬.
特称命题:,它的否定¬:,¬.
变式训练:
命题“存在R,0”的否定是
A.不存在R, >0 B.存在R, 0 C.对任意的R, 0 D.对任意的R, >0
答案:D
四、【解法小结】
1.要理解命题的四种形式,会运用逻辑推理判断真命题,利用举反例判断假命题.原命题与其逆否命题为等价命题,逆命题与否命题为等价命题,当一个命题的真假不易判断时,可考虑判断其等价命题的真假.
2.理解逻辑联结词的含义,能正确分析命题形式,指出构成它们的简单命题,并会依据真值表判断命题的真假.
3.注意一个命题的否定与命题的否命题是不同的,原命题的否定只否定结论,原命题的否命题既否定条件,又否定结论.
4.判断充要条件的三种方法是:定义法、等价法、利用集合间的包含关系作判断.
五、【布置作业】
必做题:
1. 命题:“若,则”的逆否命题是( )
A.若,则 B.若,则
C.若,则 D.若,则
2.“”是“”成立的
A.充分不必要条件 B.必要不充分条件 C.充分条件 D.既不充分也不必要条件.
3.命题“对任意的”的否定是( )
A.不存在 B.存在
C.存在 D. 对任意的
4.下列命题是真命题的为
A.若,则 B.若,则 C.若,则 D.若,则
5、设m,n是平面 内的两条不同直线,,是平面 内的两条相交直线,则// 的一个充分而不必要条件是
A.m // 且l // B. m // l 且n // l C. m // 且n // D. m // 且n // l
6.若,则的 条件.
必做题答案:1. D. 2. A 3. C. 4.A. 5. B. 6. 充分不必要条件
选做题:1.已知a>0,则x0满足关于x的方程ax = b的充要条件是
(A) (B)
(C) (D)
2.“a=1”是“函数在区间[1, +∞)上为增函数”的( )
A.充分不必要条件 B.必要不充分条件 C.充要条件 D.既不充分也不必要条件
3.已知p:有两个不等的负根,q:无实根.若p或q为真,p且q为假,求m的取值范围.
选做题答案:1.C.2. A. 3. {或}
六、【教后反思】
1.本教案的亮点是:首先以结构图呈现本章的知识结构,直观简明;其次,复习相关知识并以填空和表格的形式呈现,.再次,例题选择典型,对知识点的覆盖面广.再次,讲练结合,学生落实较好.最后,在作业的布置上,选择高考和各地市摸底考试中的部分难度不大的题,对学生理解、巩固知识能够起到良好的作用.
2.本教案的弱项:由于课时安排和时间关系,本节课内容较多,学生在课下预习时应下功夫,基础薄弱的同学可能有点跟不上或者有点吃力,课下应注意消化.
四种命题
命题及其关系
充分条件与必要条件
或
且
非或
并集
交集
补集
运算
常用逻辑用语
简单的逻辑联结词
全称命题
量词
全称量词
存在量词
含有一个量词的否定
全称量词与存在量词
特称命题
互 否
为 逆
为 逆
互 否
互 否
互 否
互 逆
原命题
若p则q
互 逆
逆命题
若q则p
逆否命题
若则
逆否命题
若则
滕州一中东校 韩霞
教学目标
重点:充要条件的判断、四种命题的关系及等价性,命题真假的判断.
难点:对一些命题真假的判断.
知识点:1.了解命题及其逆命题、否命题与逆否命题,会分析四种命题的相互关系;2.理解必要条件、充分条件与充要条件的意义; 3.了解逻辑联结词‘‘或’’‘‘且’’‘‘非’’的含义;4.理解全称量词与存在量词的意义,能正确地对含有一个量词的命题进行否定.
能力点:1.温故本章内容,使知识系统化,条理化,达到巩固与知新的效果.2.体会分类讨论,等价转化,数形结合的数学思想的应用.3.通过强化练习,培养学生分析问题解决问题的能力.
教育点:1.提高学生的逻辑思维能力;2.培养学生化归(或转化)的数学思想,分类讨论的数学思想;3.进一步提高学生的认知水平,培养学生自己解决问题的能力,为学生塑造良好的数学认识结构.
自主探究点:例题及变式的解题思路的探索.
考试点:对命题真假的判断、复合命题的构成、命题的四种形式、充要条件与必要条件的判断、全称量词与存在量词的应用.
易错易混点:充分条件与必要条件判断.
拓展点:求参数的取值范围问题.
学法与教具
学法:讲练结合、启发诱导 2.教具:多媒体、学案
一、【知识结构】
二、【知识梳理】
一.命题
1.命题的定义:我们把用语言、符号或式子表达的,可以判断真假的 叫做命题。其中判断为真的语句叫做 ,判断为假的语句叫做 .
2.命题的结构:在数学中,具有“若则”这种形式的命题中的叫做 ,叫做 .
二.四种命题及其相互关系
3.四种命题的概念:一般地,用和分别表示原命题的条件和结论,用和分别表示和的否定,于是四种命题的形式就是:
原命题:若则;逆命题: ;否命题: ;逆否命题: .
4.四种命题之间的关系
四种命题之间的相互关系如下图所示:
由上图知逆命题与否命题也互为逆否命题,因此这四种命题的真假之间的关系如下:
(1)两个命题互为逆否命题,它们具有相同的 ;
(2)两个命题为互逆命题或互否命题,它们的真假性 .
5.反证法
由于原命题与它的逆否命题具有相同的真假性,所以我们在直接证明某一命题有困难时,可以通过证明 ,来间接地证明原命题为真命题,这种证明的方法,称作是 。用反证法证明的步骤如下:
(1) ,即假设结论的反面成立;
(2)从 出发,经过推理论证得出矛盾;
(3)由矛盾判定假设不正确, .
三.充分条件与必要条件
6.若,则叫做的 条件,则叫做的 条件;
若,则叫做的 条件,简称为 条件.
7.如果且,我们称为的 条件,如果且,则我们称为的 条件.
四.判断充要条件的方法
8.命题判断法
设“若则”为原命题,那么:
(1)原命题为真,逆命题为假时,则是的 条件;
(2)原命题为假,逆命题为真时是的 条件;
(3)原命题与逆命题都为真时,是的 条件;
(4) 原命题与逆命题都为假时,是的 条件.
9.集合判断法
从集合的观点看,建立命题相应的集合:成立,成立,那么:
(1)若,则是的 条件,若时,则是的 条件;
(2) 若,则是的 条件,若时,则是的 条件;
(3)若,则是的 条件,若且时,则是的 条件.
五.逻辑联结词
10.逻辑联结词:在数学中,有时会使用一些联结词,如 .
11.“且”记作 ;“或”记作 ;“非”记作 .
12.命题,和的真假判断
(1)当都是真命题时,为 ;为 ;为 .
(2)当有一个是真命题时,为 ;为 .
(3) 当都是假命题时,为 ;为 ;为 .
上述语句可以描述为:对于“一假必假”;对于“一真必真”;对于“真假相反”。
可以用下表来判断:(即真值表)
真 真
真 假
假 真
假 假
六.全称量词与存在量词
13.全称量词:短语 、 在逻辑中通常叫做全称量词,用符号 来表示;
含有全称量词的命题,叫做 .
全称命题“对中任意一个,有成立”可用符号简记为 .
14.存在量词:短语 、 在逻辑中通常叫做存在量词,用符号 来表示;
含有存在量词的命题,叫做 .
存在命题“存在中一个,使成立” 可用符号简记为 .
15.含有一个量词的命题的否定:
全称命题:,它的否定: ;即全称命题的否定是 .
特称命题:,它的否定: ;即全称命题的否定是 .
三、【范例导航】
1.四种命题的关系
例1写出下列命题的逆命题、否命题、逆否命题,并判断它们的真假.
(1)已知,,为实数,若,则有两个不相等的实数根;
(2)若或,则;
(3)若,则,全为零.
【分析】由定义写出其逆命题、否命题、逆否命题,然后判断其真假;也可利用命题间的等价性来判断.
【解答】(1)原命题是真命题;
逆命题:若有两个不相等的实数根,则,(假);
否命题:若,则没有两个不相等的实数根,(假);
逆否命题:若没有两个不相等的实数根,则,(真).
(2)原命题是真命题;
逆命题:若,则或,是真命题;
否命题:若且,则,是真命题;
逆否命题:若,则且,是真命题.
(3)原命题是真命题;
逆命题:若,全为零,则,(真);
否命题:若,则,不全为零,(真);
逆否命题:若,不全为零,则,(真).
【点评】(1)要注意四种命题之间的等价关系,即原命题与逆否命题等价,否命题与逆命题等价.判断一个命题是真命题时,要按照数学逻辑进行推理证明,而要说明它是假命题时,只需要举出一个反例即可.
(2)在否定条件或结论时,要注意否定词语的使用.常见否定词语有:
正面词语 等于(=) 大于(>) 小于(<) 有 是 都是 全是
否定词语 不等于() 不大于() 不小于() 无 不是 不都是 不全是
正面词语 任意的 任意两个 至少有一个 至多有一个 所有的 至多有个 或
否定词语 某个 某两个 一个也没有 至少有两个 某些 至少有个 且
变式训练:
写出下列命题的否命题,并判断真假
(1)若xy=0,则x,y中至少有一个为0;
(2)若x + y =0,则x,y中至多有一个大于0.
答案:(1)否命题:若,则x,y都不为0;(真)(2)否命题:若,则x,y都大于0(假)
2.充分必要条件
例2(1) “”是“”的( )
A.充分不必要条件 B.必要不充分条件 C.充要条件 D.既不充分也不必要条件
【分析】充要条件的判断前提是先明确条件与结论,即弄清楚哪个是条件,哪个是结论,再根据条件分析出推式的关系,从而利用定义和推式得到结论.
【解答】当时,,即.
反之,当时,有,
或,即.
综上所述,“”是“”的充分不必要条件,故选A.
(2)设集合,,那么“”是“”的( )
A.充分不必要条件 B.必要不充分条件 C.充要条件 D.既不充分也不必要条件
【分析】本题条件与结论的形式都是集合形式,只要理清集合之间的关系,按照充要条件与集合的对应关系即可作出判断.
【解答】∵,∴.故选A.
【点评】在从条件推结论,结论推条件时,可以利用学过的定理、定义和公式直接做逻辑判断,或利用数轴或Venn图分析两个集合的关系判断出“”和“”的真假.
例3已知是的充分条件而不必要条件,是的充分条件,是的必要条件,是的必要条件.现有下列命题:①是的充要条件;②是的充分而不必要条件;③是的必要而不充分条件;④的必要而不充分条件;⑤是的充分而不必要条件,则正确命题序号是( )
A.①④⑤ B.①②④ C.②③⑤ D.②④⑤
【分析】本题命题及其关系较多,如果直接解决则比较麻烦,可以用符号“”、“”等符号表示,简化题意,解决方便.
【解答】由题意可知:,且,.
所以,①正确;,且,②正确;,③不正确;
,且,④正确;,⑤不正确.故选B.
【点评】(1)本题考查了充分条件、必要条件、充要条件的概念及命题之间关系的转化,逆否命题的等价性,考查了逻辑思辩能力和转化思想.
(2)在命题之间的充分条件、必要条件、充要条件的推导过程中,使用符号语言可以简化过程,降低思维量.
变式训练:
已知命题:,命题:,若¬是¬的充分不必要条件,求实数的取值范围.
答案:.
3. 命题真假的判断
例4(1)已知命题:所有有理数都是实数,命题:正数的对数都是负数,则下列命题中为真命题的是
A. B. C. D.
【分析】本题只需要判断出命题和命题的真假,根据真值表进行判断即可.
【解答】由题意可以判断命题是真命题,命题是假命题,所以命题是假命题,命题是真命题.只有是真命题,故选D.
【点评】命题的真假判断是“一真必真”;命题的真假判断是“一假必假”;命题与的真假相反.
变式训练:
有四个关于三角函数的命题:
:, :、,
:, :
其中是假命题的有( )
A., B., C., D.,
答案:A.
4.命题的否定
例5已知命题:,则( )
A. B.C. D.
【分析】对全称(特称)命题的否定是将其全称(存在)量词改为存在(全称)量词,再将结论否定.
【解答】将变为,同时否定,可以得到,故选C.
【点评】一般地,对于含有一个量词的全称命题的否定,有下面的结论:
全称命题:,它的否定¬:,¬.
特称命题:,它的否定¬:,¬.
变式训练:
命题“存在R,0”的否定是
A.不存在R, >0 B.存在R, 0 C.对任意的R, 0 D.对任意的R, >0
答案:D
四、【解法小结】
1.要理解命题的四种形式,会运用逻辑推理判断真命题,利用举反例判断假命题.原命题与其逆否命题为等价命题,逆命题与否命题为等价命题,当一个命题的真假不易判断时,可考虑判断其等价命题的真假.
2.理解逻辑联结词的含义,能正确分析命题形式,指出构成它们的简单命题,并会依据真值表判断命题的真假.
3.注意一个命题的否定与命题的否命题是不同的,原命题的否定只否定结论,原命题的否命题既否定条件,又否定结论.
4.判断充要条件的三种方法是:定义法、等价法、利用集合间的包含关系作判断.
五、【布置作业】
必做题:
1. 命题:“若,则”的逆否命题是( )
A.若,则 B.若,则
C.若,则 D.若,则
2.“”是“”成立的
A.充分不必要条件 B.必要不充分条件 C.充分条件 D.既不充分也不必要条件.
3.命题“对任意的”的否定是( )
A.不存在 B.存在
C.存在 D. 对任意的
4.下列命题是真命题的为
A.若,则 B.若,则 C.若,则 D.若,则
5、设m,n是平面 内的两条不同直线,,是平面 内的两条相交直线,则// 的一个充分而不必要条件是
A.m // 且l // B. m // l 且n // l C. m // 且n // D. m // 且n // l
6.若,则的 条件.
必做题答案:1. D. 2. A 3. C. 4.A. 5. B. 6. 充分不必要条件
选做题:1.已知a>0,则x0满足关于x的方程ax = b的充要条件是
(A) (B)
(C) (D)
2.“a=1”是“函数在区间[1, +∞)上为增函数”的( )
A.充分不必要条件 B.必要不充分条件 C.充要条件 D.既不充分也不必要条件
3.已知p:有两个不等的负根,q:无实根.若p或q为真,p且q为假,求m的取值范围.
选做题答案:1.C.2. A. 3. {或}
六、【教后反思】
1.本教案的亮点是:首先以结构图呈现本章的知识结构,直观简明;其次,复习相关知识并以填空和表格的形式呈现,.再次,例题选择典型,对知识点的覆盖面广.再次,讲练结合,学生落实较好.最后,在作业的布置上,选择高考和各地市摸底考试中的部分难度不大的题,对学生理解、巩固知识能够起到良好的作用.
2.本教案的弱项:由于课时安排和时间关系,本节课内容较多,学生在课下预习时应下功夫,基础薄弱的同学可能有点跟不上或者有点吃力,课下应注意消化.
四种命题
命题及其关系
充分条件与必要条件
或
且
非或
并集
交集
补集
运算
常用逻辑用语
简单的逻辑联结词
全称命题
量词
全称量词
存在量词
含有一个量词的否定
全称量词与存在量词
特称命题
互 否
为 逆
为 逆
互 否
互 否
互 否
互 逆
原命题
若p则q
互 逆
逆命题
若q则p
逆否命题
若则
逆否命题
若则
