湖南省株洲市醴陵市2021-2022学年八年级下学期期末质量检测数学试题(word版含答案)
文档属性
| 名称 | 湖南省株洲市醴陵市2021-2022学年八年级下学期期末质量检测数学试题(word版含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 470.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 湘教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-07-08 20:48:26 | ||
图片预览

文档简介
2022上学期八年级期末质量检测
数学试卷
总分:150 分;时量:120 分钟;
一、选择题(共10小题,每小题4分,共40分)
1.第24届冬奥会于2022年2月4日在北京开幕,北京成为全球首个既举办过夏季奥运会又举办过冬季奥运会的城市.下列各届冬奥会会徽部分图案中,是中心对称图形的是( )
A. B. C. D.
2.已知,在直角△ABC中,∠C为直角,∠B是∠A的2倍,则∠A的度数是( )
A. B. C. D.
3.在平面直角坐标系中,将绕原点旋转180°,得到的对应点的坐标( )
A. B. C. D.
4.在平面直角坐标系中,将直线y=2x+b沿y轴向上平移3个单位后恰好经过原点,则b的值为( )
A.﹣3 B.2 C.﹣2 D.3
5.下列命题是真命题的是( )
A.对角线相等的平行四边形是菱形. B.有一组邻边相等的平行四边形是菱形.
C.对角线相互垂直且相等的四边形是菱形.D.有一组对边平行且相等的四边形是菱形.
6.下列长度的四组线段中,可以构成直角三角形的一组是( )
A.,, B.0.3,0.4,0.5 C.1,,3 D.2,3,4
7.在平面直角坐标系中,平行四边形的顶点,,的坐标分别是,,,则顶点的坐标是( )
A. B. C. D.
第7题 第8题 第9题
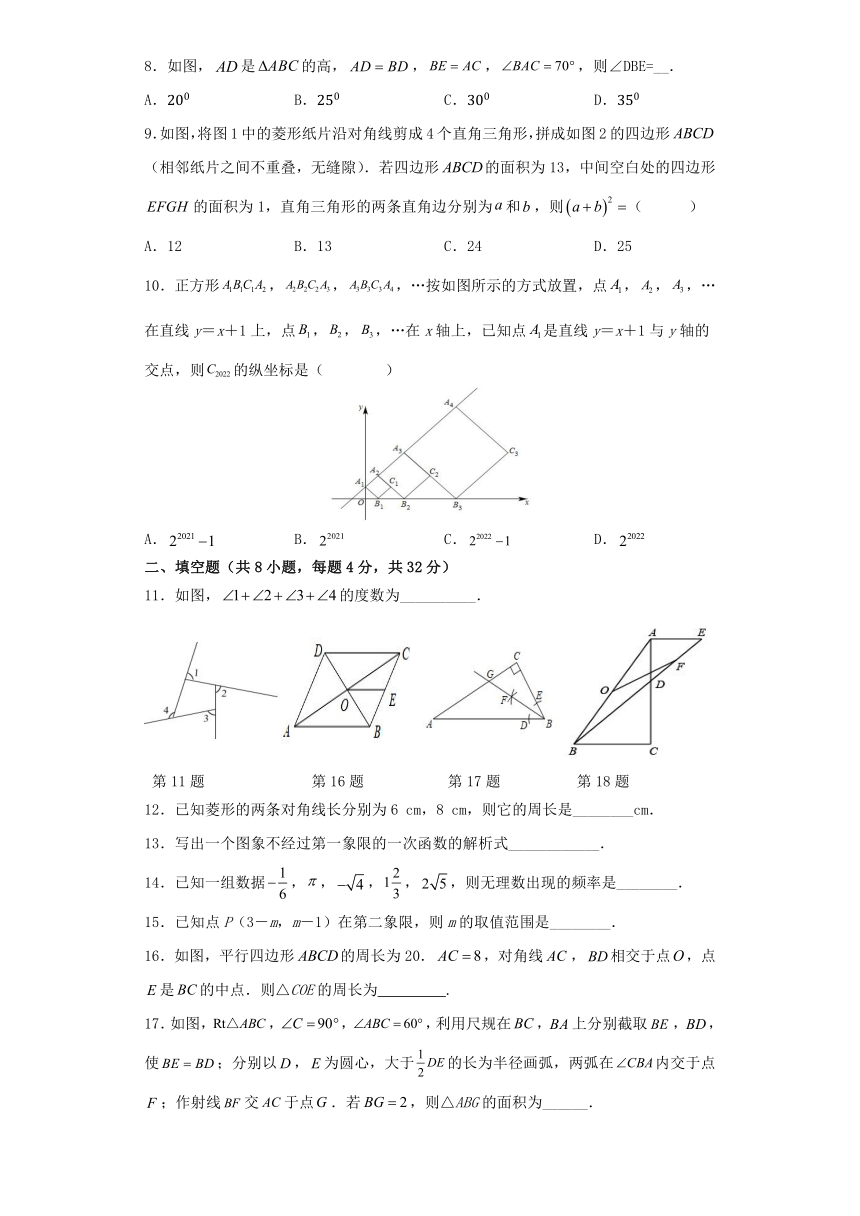
8.如图,是的高,,,,则∠DBE=__.
A. B. C. D.
9.如图,将图1中的菱形纸片沿对角线剪成4个直角三角形,拼成如图2的四边形(相邻纸片之间不重叠,无缝隙).若四边形的面积为13,中间空白处的四边形的面积为1,直角三角形的两条直角边分别为和,则( )
A.12 B.13 C.24 D.25
10.正方形,,,…按如图所示的方式放置,点,,,…在直线y=x+1上,点,,,…在x轴上,已知点是直线y=x+1与y轴的交点,则的纵坐标是( )
A. B. C. D.
二、填空题(共8小题,每题4分,共32分)
11.如图,的度数为__________.
第11题 第16题 第17题 第18题
12.已知菱形的两条对角线长分别为6 cm,8 cm,则它的周长是________cm.
13.写出一个图象不经过第一象限的一次函数的解析式____________.
14.已知一组数据,,,,,则无理数出现的频率是________.
15.已知点P(3-m,m-1)在第二象限,则m的取值范围是________.
16.如图,平行四边形的周长为20.,对角线,相交于点,点是的中点.则△COE的周长为 .
17.如图,,,,利用尺规在,上分别截取,,使;分别以,为圆心,大于的长为半径画弧,两弧在内交于点;作射线交于点.若,则△ABG的面积为______.
18.如图,在Rt△ABC中,∠C=90°,点O为AB的中点,点D在线段AC上,过点A作BC的平行线交直线BD于点E,点F是DE的中点,连接OF,若AD=AE=2,BC=4,则OF的长为 .
三、解答题(共8道,19题6分,20-21题每题8分,22—24题每题10分,25-26题每题13分,共78分)
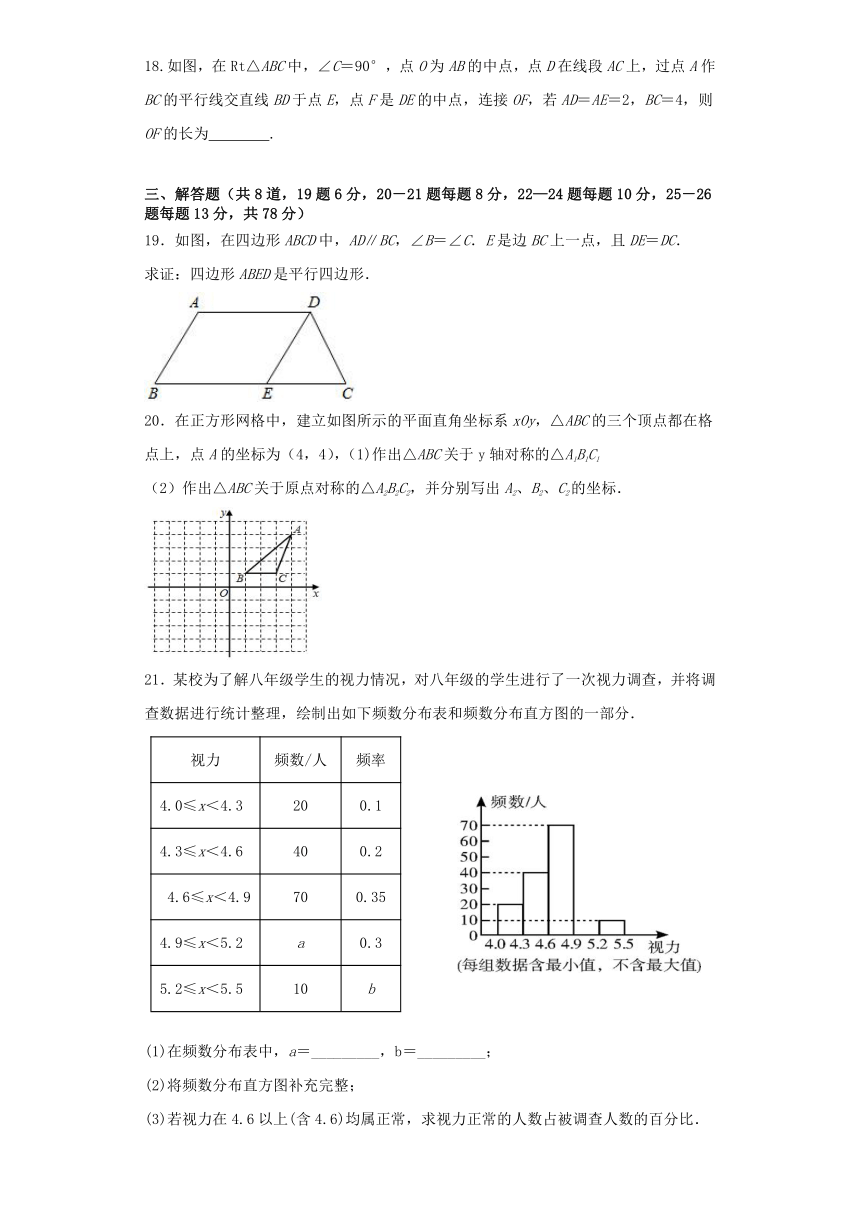
19.如图,在四边形ABCD中,AD∥BC,∠B=∠C.E是边BC上一点,且DE=DC.
求证:四边形ABED是平行四边形.
在正方形网格中,建立如图所示的平面直角坐标系xOy,△ABC的三个顶点都在格点上,点A的坐标为(4,4),(1)作出△ABC关于y轴对称的△A1B1C1
(2)作出△ABC关于原点对称的△A2B2C2,并分别写出A2、B2、C2的坐标.
21.某校为了解八年级学生的视力情况,对八年级的学生进行了一次视力调查,并将调查数据进行统计整理,绘制出如下频数分布表和频数分布直方图的一部分.
视力 频数/人 频率
4.0≤x<4.3 20 0.1
4.3≤x<4.6 40 0.2
4.6≤x<4.9 70 0.35
4.9≤x<5.2 a 0.3
5.2≤x<5.5 10 b
(1)在频数分布表中,a=_________,b=_________;
(2)将频数分布直方图补充完整;
(3)若视力在4.6以上(含4.6)均属正常,求视力正常的人数占被调查人数的百分比.
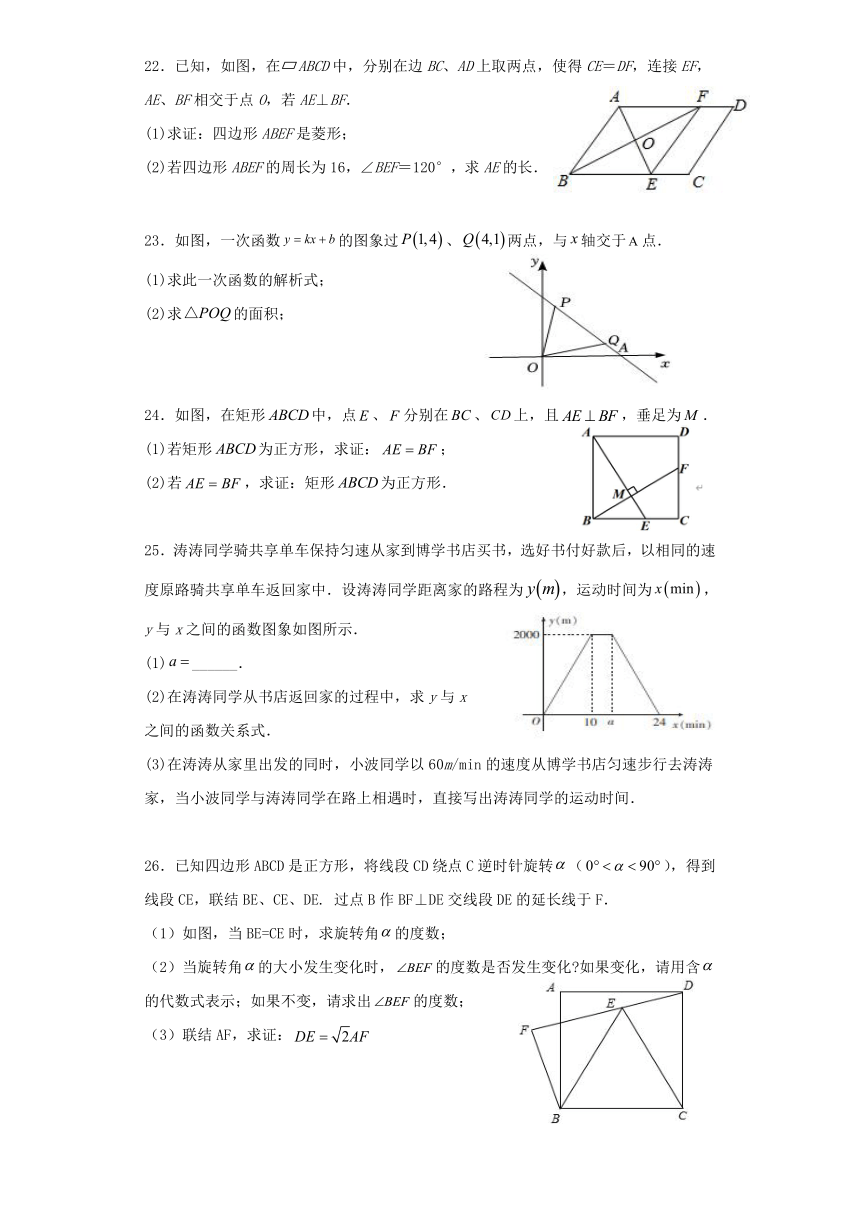
22.已知,如图,在 ABCD中,分别在边BC、AD上取两点,使得CE=DF,连接EF,AE、BF相交于点O,若AE⊥BF.
(1)求证:四边形ABEF是菱形;
(2)若四边形ABEF的周长为16,∠BEF=120°,求AE的长.
23.如图,一次函数的图象过、两点,与轴交于点.
(1)求此一次函数的解析式;
(2)求的面积;
24.如图,在矩形中,点、分别在、上,且,垂足为.
(1)若矩形为正方形,求证:;
(2)若,求证:矩形为正方形.
25.涛涛同学骑共享单车保持匀速从家到博学书店买书,选好书付好款后,以相同的速度原路骑共享单车返回家中.设涛涛同学距离家的路程为,运动时间为,y与x之间的函数图象如图所示.
(1)______.
(2)在涛涛同学从书店返回家的过程中,求y与x之间的函数关系式.
(3)在涛涛从家里出发的同时,小波同学以60m/min的速度从博学书店匀速步行去涛涛家,当小波同学与涛涛同学在路上相遇时,直接写出涛涛同学的运动时间.
26.已知四边形ABCD是正方形,将线段CD绕点C逆时针旋转(),得到线段CE,联结BE、CE、DE. 过点B作BF⊥DE交线段DE的延长线于F.
(1)如图,当BE=CE时,求旋转角的度数;
(2)当旋转角的大小发生变化时,的度数是否发生变化 如果变化,请用含的代数式表示;如果不变,请求出的度数;
(3)联结AF,求证:
2022年上学期期末质量检测八年级数学参考答案
(阅卷前请老师们先斟酌一下)
总分150分,时量120分钟
选择题(共10小题,每小题4分,共40分)
题号 1 2 3 4 5 6 7 8 9 10
答案 C A D A B B C B D B
二、填空题(共8小题,每题4分,共32分)
11. 12.20 13、 (答案不唯一) 14.
15. 16.9, 17. 18.
三、解答题(共8道,19题6分,20-21题每题8分,22—24题每题10分,25-26题每题13分,
共78分)
19.证明:∵DE=DC,
∴∠DEC=∠C. ……………2’
∵∠B=∠C,
∴∠B=∠DEC,
∴AB∥DE, ……………4’
∵AD∥BC,
∴四边形ABED是平行四边形. ……………6’
20.解:(1)如图,△A1B1C1即为所求;……………3’
(2)如图,△A2B2C2即为所求;……………5’
A2(-4,-4),B2(-1,-1),C2(-3,-1)……………8’
21.(1)60,0.05 ……………4’
……………6’
(3)视力正常人数占被调查人数的百分比是0.35+0.3+0.05=0.7=70% ……………8’
22.证明:四边形是平行四边形,
,,
又,
,
四边形是平行四边形, ……………3’
又,
四边形是菱形; ……………5’
(2)解:菱形的周长为16,
,,
,
是等边三角形,
. ……………10’
23.(1)解:根据题意得, 解得,
此一次函数的解析式为; ……………5’
(2)当时,,解得,则, ……………7’
; ……………10’
24.(1)证明:∵四边形是正方形,
∴, ,
∴,
又∵,
∴,
∴, ……………3’
在和中
∴(),
∴. ……………5’
(2)证明:∵四边形是矩形,
∴ ,
∴,
∵,
∴,
∴, ……………7’
在和中
∴(), ……………8’
∴,
又∵四边形是矩形,
∴四边形是正方形. ……………10’
25.(1)14 ……………4’
(2)设y与x之间的函数关系式为,
将与代入,得,
解得,
∴y与x之间的函数关系式为:. ……………9’
(3)或20min(可以不写过程,少写一个答案扣2分) ……………13’
涛涛骑车的速度为
设涛涛从家里出发min后,两人相遇,
①涛涛同学去书店时与小波同学相遇,
解得
②涛涛同学返回时与小波同学相遇,
解得
综上所述,当小波同学与涛涛同学在路上相遇时,直接写出涛涛同学的运动时间为或20min.
(1)证明:在正方形ABCD中, BC=CD.
由旋转知,CE=CD,
又∵BE=CE,
∴BE=CE=BC,
∴△BEC是等边三角形,
∴∠BCE=60°.
又∵∠BCD=90°,
∴=∠DCE=30°. ……………4’
(2)∠BEF的度数不发生变化. ……………5’
在△CED中,CE=CD,
∴∠CED=∠CDE=,
在△CEB中,CE=CB,∠BCE=,
∴∠CEB=∠CBE=, ……………7’
∴∠BEF=. ……………8’
(3)过点A作AG∥DF与BF的延长线交于点G,过点A作AH∥GF与DF交于点H,过点C作CI⊥DF于点I
易知四边形AGFH是平行四边形,
又∵BF⊥DF,
∴平行四边形AGFH是矩形.
∵∠BAD=∠BGF=90°,
∠BPF=∠APD ,
∴∠ABG=∠ADH.
又∵∠AGB=∠AHD=90°,AB=AD,
∴△ABG≌△ADH.
∴AG=AH ,
∴矩形AGFH是正方形. ……………10’
∴∠AFH=∠FAH=45°,
∴AH=AF
∵∠DAH+∠ADH=∠CDI+∠ADH=90°
∴∠DAH=∠CDI
又∵∠AHD=∠DIC=90°,AD=DC,
∴△AHD≌△DIC
∴AH=DI,
∵DE=2DI,
∴DE=2AH=AF ……………13’
数学试卷
总分:150 分;时量:120 分钟;
一、选择题(共10小题,每小题4分,共40分)
1.第24届冬奥会于2022年2月4日在北京开幕,北京成为全球首个既举办过夏季奥运会又举办过冬季奥运会的城市.下列各届冬奥会会徽部分图案中,是中心对称图形的是( )
A. B. C. D.
2.已知,在直角△ABC中,∠C为直角,∠B是∠A的2倍,则∠A的度数是( )
A. B. C. D.
3.在平面直角坐标系中,将绕原点旋转180°,得到的对应点的坐标( )
A. B. C. D.
4.在平面直角坐标系中,将直线y=2x+b沿y轴向上平移3个单位后恰好经过原点,则b的值为( )
A.﹣3 B.2 C.﹣2 D.3
5.下列命题是真命题的是( )
A.对角线相等的平行四边形是菱形. B.有一组邻边相等的平行四边形是菱形.
C.对角线相互垂直且相等的四边形是菱形.D.有一组对边平行且相等的四边形是菱形.
6.下列长度的四组线段中,可以构成直角三角形的一组是( )
A.,, B.0.3,0.4,0.5 C.1,,3 D.2,3,4
7.在平面直角坐标系中,平行四边形的顶点,,的坐标分别是,,,则顶点的坐标是( )
A. B. C. D.
第7题 第8题 第9题
8.如图,是的高,,,,则∠DBE=__.
A. B. C. D.
9.如图,将图1中的菱形纸片沿对角线剪成4个直角三角形,拼成如图2的四边形(相邻纸片之间不重叠,无缝隙).若四边形的面积为13,中间空白处的四边形的面积为1,直角三角形的两条直角边分别为和,则( )
A.12 B.13 C.24 D.25
10.正方形,,,…按如图所示的方式放置,点,,,…在直线y=x+1上,点,,,…在x轴上,已知点是直线y=x+1与y轴的交点,则的纵坐标是( )
A. B. C. D.
二、填空题(共8小题,每题4分,共32分)
11.如图,的度数为__________.
第11题 第16题 第17题 第18题
12.已知菱形的两条对角线长分别为6 cm,8 cm,则它的周长是________cm.
13.写出一个图象不经过第一象限的一次函数的解析式____________.
14.已知一组数据,,,,,则无理数出现的频率是________.
15.已知点P(3-m,m-1)在第二象限,则m的取值范围是________.
16.如图,平行四边形的周长为20.,对角线,相交于点,点是的中点.则△COE的周长为 .
17.如图,,,,利用尺规在,上分别截取,,使;分别以,为圆心,大于的长为半径画弧,两弧在内交于点;作射线交于点.若,则△ABG的面积为______.
18.如图,在Rt△ABC中,∠C=90°,点O为AB的中点,点D在线段AC上,过点A作BC的平行线交直线BD于点E,点F是DE的中点,连接OF,若AD=AE=2,BC=4,则OF的长为 .
三、解答题(共8道,19题6分,20-21题每题8分,22—24题每题10分,25-26题每题13分,共78分)
19.如图,在四边形ABCD中,AD∥BC,∠B=∠C.E是边BC上一点,且DE=DC.
求证:四边形ABED是平行四边形.
在正方形网格中,建立如图所示的平面直角坐标系xOy,△ABC的三个顶点都在格点上,点A的坐标为(4,4),(1)作出△ABC关于y轴对称的△A1B1C1
(2)作出△ABC关于原点对称的△A2B2C2,并分别写出A2、B2、C2的坐标.
21.某校为了解八年级学生的视力情况,对八年级的学生进行了一次视力调查,并将调查数据进行统计整理,绘制出如下频数分布表和频数分布直方图的一部分.
视力 频数/人 频率
4.0≤x<4.3 20 0.1
4.3≤x<4.6 40 0.2
4.6≤x<4.9 70 0.35
4.9≤x<5.2 a 0.3
5.2≤x<5.5 10 b
(1)在频数分布表中,a=_________,b=_________;
(2)将频数分布直方图补充完整;
(3)若视力在4.6以上(含4.6)均属正常,求视力正常的人数占被调查人数的百分比.
22.已知,如图,在 ABCD中,分别在边BC、AD上取两点,使得CE=DF,连接EF,AE、BF相交于点O,若AE⊥BF.
(1)求证:四边形ABEF是菱形;
(2)若四边形ABEF的周长为16,∠BEF=120°,求AE的长.
23.如图,一次函数的图象过、两点,与轴交于点.
(1)求此一次函数的解析式;
(2)求的面积;
24.如图,在矩形中,点、分别在、上,且,垂足为.
(1)若矩形为正方形,求证:;
(2)若,求证:矩形为正方形.
25.涛涛同学骑共享单车保持匀速从家到博学书店买书,选好书付好款后,以相同的速度原路骑共享单车返回家中.设涛涛同学距离家的路程为,运动时间为,y与x之间的函数图象如图所示.
(1)______.
(2)在涛涛同学从书店返回家的过程中,求y与x之间的函数关系式.
(3)在涛涛从家里出发的同时,小波同学以60m/min的速度从博学书店匀速步行去涛涛家,当小波同学与涛涛同学在路上相遇时,直接写出涛涛同学的运动时间.
26.已知四边形ABCD是正方形,将线段CD绕点C逆时针旋转(),得到线段CE,联结BE、CE、DE. 过点B作BF⊥DE交线段DE的延长线于F.
(1)如图,当BE=CE时,求旋转角的度数;
(2)当旋转角的大小发生变化时,的度数是否发生变化 如果变化,请用含的代数式表示;如果不变,请求出的度数;
(3)联结AF,求证:
2022年上学期期末质量检测八年级数学参考答案
(阅卷前请老师们先斟酌一下)
总分150分,时量120分钟
选择题(共10小题,每小题4分,共40分)
题号 1 2 3 4 5 6 7 8 9 10
答案 C A D A B B C B D B
二、填空题(共8小题,每题4分,共32分)
11. 12.20 13、 (答案不唯一) 14.
15. 16.9, 17. 18.
三、解答题(共8道,19题6分,20-21题每题8分,22—24题每题10分,25-26题每题13分,
共78分)
19.证明:∵DE=DC,
∴∠DEC=∠C. ……………2’
∵∠B=∠C,
∴∠B=∠DEC,
∴AB∥DE, ……………4’
∵AD∥BC,
∴四边形ABED是平行四边形. ……………6’
20.解:(1)如图,△A1B1C1即为所求;……………3’
(2)如图,△A2B2C2即为所求;……………5’
A2(-4,-4),B2(-1,-1),C2(-3,-1)……………8’
21.(1)60,0.05 ……………4’
……………6’
(3)视力正常人数占被调查人数的百分比是0.35+0.3+0.05=0.7=70% ……………8’
22.证明:四边形是平行四边形,
,,
又,
,
四边形是平行四边形, ……………3’
又,
四边形是菱形; ……………5’
(2)解:菱形的周长为16,
,,
,
是等边三角形,
. ……………10’
23.(1)解:根据题意得, 解得,
此一次函数的解析式为; ……………5’
(2)当时,,解得,则, ……………7’
; ……………10’
24.(1)证明:∵四边形是正方形,
∴, ,
∴,
又∵,
∴,
∴, ……………3’
在和中
∴(),
∴. ……………5’
(2)证明:∵四边形是矩形,
∴ ,
∴,
∵,
∴,
∴, ……………7’
在和中
∴(), ……………8’
∴,
又∵四边形是矩形,
∴四边形是正方形. ……………10’
25.(1)14 ……………4’
(2)设y与x之间的函数关系式为,
将与代入,得,
解得,
∴y与x之间的函数关系式为:. ……………9’
(3)或20min(可以不写过程,少写一个答案扣2分) ……………13’
涛涛骑车的速度为
设涛涛从家里出发min后,两人相遇,
①涛涛同学去书店时与小波同学相遇,
解得
②涛涛同学返回时与小波同学相遇,
解得
综上所述,当小波同学与涛涛同学在路上相遇时,直接写出涛涛同学的运动时间为或20min.
(1)证明:在正方形ABCD中, BC=CD.
由旋转知,CE=CD,
又∵BE=CE,
∴BE=CE=BC,
∴△BEC是等边三角形,
∴∠BCE=60°.
又∵∠BCD=90°,
∴=∠DCE=30°. ……………4’
(2)∠BEF的度数不发生变化. ……………5’
在△CED中,CE=CD,
∴∠CED=∠CDE=,
在△CEB中,CE=CB,∠BCE=,
∴∠CEB=∠CBE=, ……………7’
∴∠BEF=. ……………8’
(3)过点A作AG∥DF与BF的延长线交于点G,过点A作AH∥GF与DF交于点H,过点C作CI⊥DF于点I
易知四边形AGFH是平行四边形,
又∵BF⊥DF,
∴平行四边形AGFH是矩形.
∵∠BAD=∠BGF=90°,
∠BPF=∠APD ,
∴∠ABG=∠ADH.
又∵∠AGB=∠AHD=90°,AB=AD,
∴△ABG≌△ADH.
∴AG=AH ,
∴矩形AGFH是正方形. ……………10’
∴∠AFH=∠FAH=45°,
∴AH=AF
∵∠DAH+∠ADH=∠CDI+∠ADH=90°
∴∠DAH=∠CDI
又∵∠AHD=∠DIC=90°,AD=DC,
∴△AHD≌△DIC
∴AH=DI,
∵DE=2DI,
∴DE=2AH=AF ……………13’
同课章节目录
