不等关系与不等式

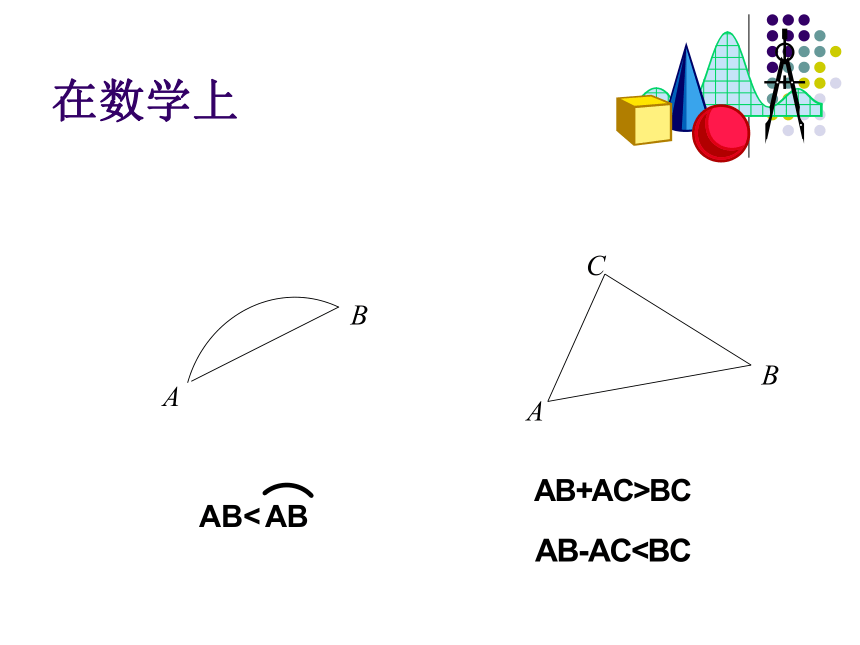
课件21张PPT。3.1不等关系与不等式 现实世界和日常生活中，既有相等关系，又存在着大量的不等关系．如两点之间线段最短，三角形两边之和大于第三边，等等．这种不等关系都可用不等式来表示．不等关系和不等式一.问题情境实际生活中长短大小轻重高矮在数学上实例演示这是神州六号发射升空时
的场景，发射要成功它的
速度必须满足怎样的条件？v≥7.9 km/s那么在飞行时呢？v≤7.9 km/s限速40 km/h的路标，指示司机在前方路段行驶时，应使汽车的速度v不超40 km/h，写成式子是：km/h这是某酸奶的质量检查规定用数学关系来反映就是：从表格中你能获得什么信息？不等式 用不等号（＜、＞、≤、≥、≠）表示不等关系的式子叫不等式。 “不等号”是英国数学家哈里奥特（T.Harriot）于1631年开始使用的，但当时并没有被数学界所接受，直到100多年后，才逐渐成为标准的应用符号。
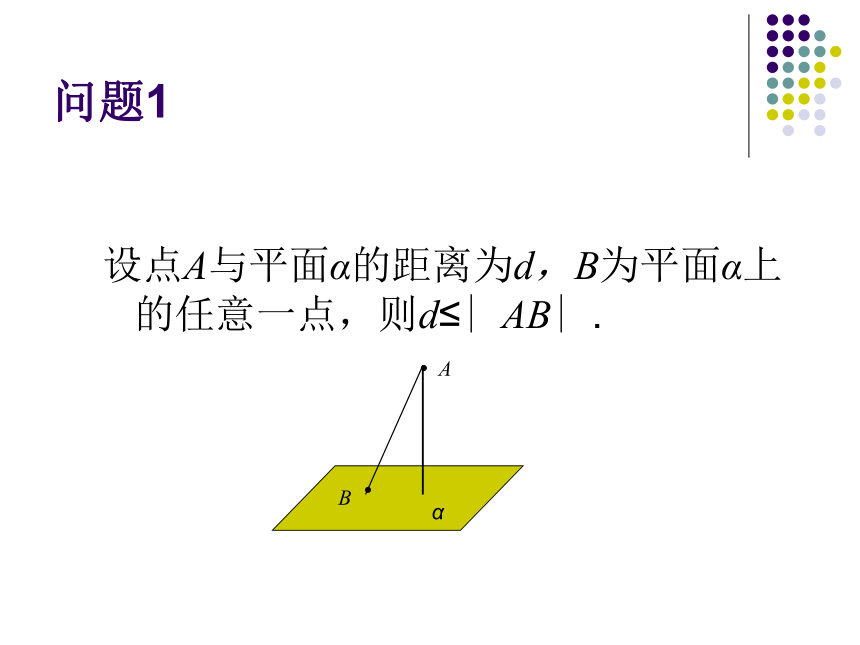
一、用不等式（组）来表示不等关系问题1设点A与平面α的距离为d，B为平面α上的任意一点，则d≤∣AB∣.ABα某种杂志原以每本2.5元的价格销售，可以售出8万本。据市场调查，若单价每提高0.1元，销售量就可能相应减少2 000本。若把提价后杂志的定价设为x元，怎样用不等式表示销售的总收入仍不低于20万元呢？问题2问题2分析：设杂志社的定价为x元，则销售的总收入为
万元，那么不等关系“销售的总收入仍不低于20万元”可以表示为不等式： 某钢铁厂要把长度为4000 mm的钢管截成500 mm和600 mm两种。按照生产的要求，600 mm的数量不能超过500 mm钢管的3倍。怎样写出满足所有上述不等关系的不等式呢？问题3问题3解：假设截得500 mm的钢管x根，截得600 mm的钢管y根。根据题意，应有如下的不等关系：三、不等式基本原理a - b > 0 <=> a > b
a - b = 0 <=> a = b
a - b < 0 <=> a < b比较两个实数a与b的大小，归结为判断它们的差a-b的符号；比较两个代数式的大小，实际上是比较它们的值的大小，而这又归结为判断它们的差的符号．第74页 自学探究1）不等式的两边同时加上或减去同一个数，不等号的方向不改变，即
2）不等式的两边同时乘以或除以同一个正数，不等号的方向不改变，即
3）不等式的两边同时乘以或除以同一个负数，不等号的方向改变，即不等式的性质若a>b,则a±c>b±c复习若a>b且c>0,则ac>bc若a>b且c<0,则ac a - b > 0 <=> a > b
a - b = 0 <=> a = b
a - b < 0 <=> a < b
4．作差比较法
步骤：作差，变形，定号