24.1.4.1圆周角(2) 课件(共21张PPT)
文档属性
| 名称 | 24.1.4.1圆周角(2) 课件(共21张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 1.0MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-07-10 21:02:41 | ||
图片预览






文档简介
(共21张PPT)
24.1.4.1圆周角(2)
人教版九年级上册
教学目标
教学目标: 1.了解并证明圆周角定理的推论:圆内接四边形的对角互补.
2.能应用圆周角定理及其推论解决问题.
教学重点:圆内接四边形的性质定理.
教学难点:圆内接四边形性质定理的准确、灵活应用.
新知导入
情境引入
复习旧知:
1、还记得圆周角的定义吗?
2、请你说出圆周角定理及推论。
圆周角定理:一条弧所对的圆周角等于它所对圆心角的一半.
推论1:同弧或等弧所对的圆周角相等.
推论2:半圆(或直径)所对的圆周角是直角,90°的圆周角所对的弦是直径.
新知讲解
合作学习
你能说出下列多边形的名称吗?
三角形
五边形
六边形
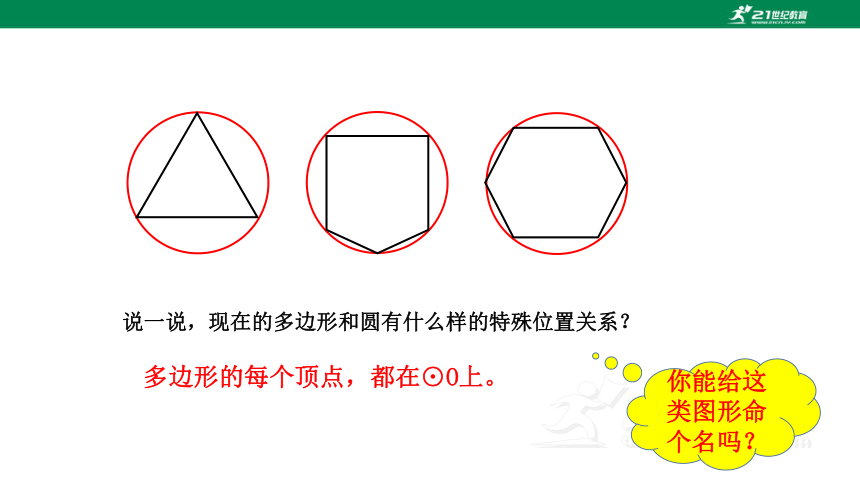
说一说,现在的多边形和圆有什么样的特殊位置关系?
多边形的每个顶点,都在⊙O上。
你能给这类图形命个名吗?
提炼概念
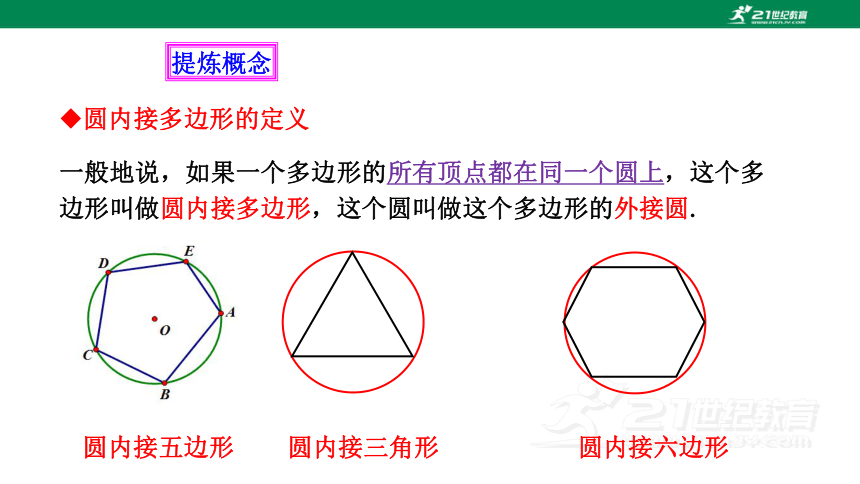
一般地说,如果一个多边形的所有顶点都在同一个圆上,这个多边形叫做圆内接多边形,这个圆叫做这个多边形的外接圆.
圆内接多边形的定义
圆内接五边形
圆内接六边形
圆内接三角形
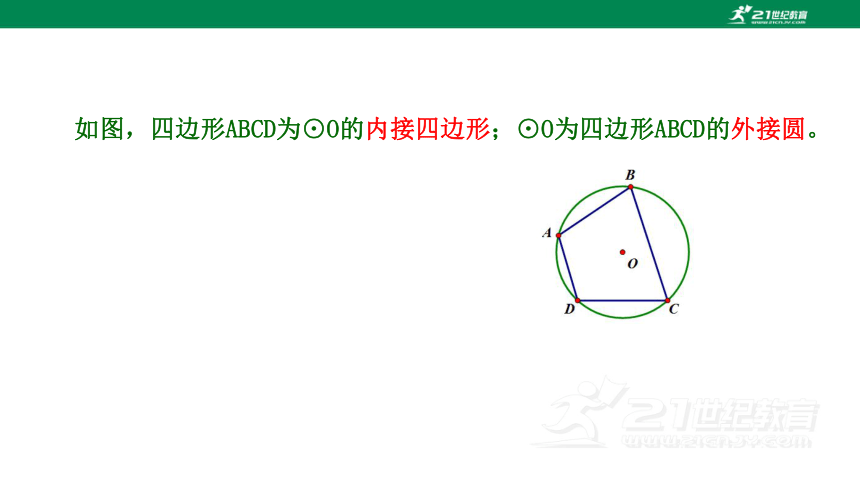
如图,四边形ABCD为⊙O的内接四边形;⊙O为四边形ABCD的外接圆。
我们再来看圆内接四边形有什么性质.
猜想:∠A与∠C, ∠B与∠D之间的关系为∠A+ ∠C=180 ,∠B+ ∠D=180
如图,四边形ABCD是⊙O的内接四边形,那么其相对的两个内角之间是什么关系?请你证明这个结论.
证明:连接OB,OD
在⊙O中,∠A所对的弧为BCD,∠C所对的弧为BAD.
)
)
又∵BCD与BCD所对的圆心角的度数之和为360°,
同理:∠B+∠D=180°.
得出结论:圆内接四边形对角互补.
几何语言:
∵四边形ABCD内接于⊙O
∴∠A+∠C=180°,∠B+∠D=180°
)
)
典例精讲
合作探究
例、求证:圆内接四边形的任何一个外角都等于它的内对角.
已知:如图,四边形 ABCD是⊙O的内接四边形.
求证:∠DCE=∠A.
证明:∵∠DCE+∠BCD=180°,
又∵∠A+∠BCD=180°,
∴∠DCE=∠A.
类似的:∠MBC=∠ADC
∠ADF=∠ABC
外角
内对角
F
M
归纳概念
合作探究
圆周角
圆周角定理的推论
圆内接四边形
圆内接四边形的对角互补.
推论一:同弧或等弧所对的圆周角相等.
推论二:同弧或等弧所对的圆周角相等.半圆(或直径)所对的圆周角是直角,90°的圆周角所对的弦是直径.
课堂练习
1.如图 ,四边形 ABCD 是圆内接四边形,点 E 是BC 延长线上一点,若∠BAD=105°,则∠DCE 的大小是( )
A.115° B.105° C.100° D.95°
B
2.如图 ,点A,B,C,D,E 五等分圆,则∠A+∠B+∠C+∠D+∠E=( )
A.180° B.150° C.135° D.120°
A
3.如图,点B,C,D在⊙O上,若∠BCD=130°,则∠BOD的度数是 .
1000
4.如图,已知四边形 ABCD 内接于⊙O,∠BOD =80°,求∠BAD 和∠BCD 的度数.
解:∵∠BOD=80°
∴∠BAD=40°.
又∵ABCD是圆的内接四边形,
∴∠BAD+∠BCD=180°,
∴∠BCD=140°.
5.如图,在⊙O的内接四边形ABCD中,∠BCD=120°,CA平分∠BCD.
(1)求证:△ABD是等边三角形;
(2)若BD=3,求⊙O的半径.
解:(1)∵∠BCD=120°,CA平分∠BCD,
∴∠ACD=∠ACB=60°,
由圆周角定理得,∠ADB=∠ACB=60°,∠ABD=∠ACD=60°,
∴△ABD是等边三角形;
∴⊙O的半径为
(2)连接OB、OD,作OH⊥BD于H,
则DH= BD= ,
∠BOD=2∠BAD=120°,
∴∠DOH=60°,
在Rt△ODH中,OD=
课堂总结
圆周角
圆内接四边形
圆内接四边形的对角互补.
作业布置
教材课后配套作业题。
谢谢
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
兼职招聘:
https://www.21cnjy.com/recruitment/home/admin
24.1.4.1圆周角(2)
人教版九年级上册
教学目标
教学目标: 1.了解并证明圆周角定理的推论:圆内接四边形的对角互补.
2.能应用圆周角定理及其推论解决问题.
教学重点:圆内接四边形的性质定理.
教学难点:圆内接四边形性质定理的准确、灵活应用.
新知导入
情境引入
复习旧知:
1、还记得圆周角的定义吗?
2、请你说出圆周角定理及推论。
圆周角定理:一条弧所对的圆周角等于它所对圆心角的一半.
推论1:同弧或等弧所对的圆周角相等.
推论2:半圆(或直径)所对的圆周角是直角,90°的圆周角所对的弦是直径.
新知讲解
合作学习
你能说出下列多边形的名称吗?
三角形
五边形
六边形
说一说,现在的多边形和圆有什么样的特殊位置关系?
多边形的每个顶点,都在⊙O上。
你能给这类图形命个名吗?
提炼概念
一般地说,如果一个多边形的所有顶点都在同一个圆上,这个多边形叫做圆内接多边形,这个圆叫做这个多边形的外接圆.
圆内接多边形的定义
圆内接五边形
圆内接六边形
圆内接三角形
如图,四边形ABCD为⊙O的内接四边形;⊙O为四边形ABCD的外接圆。
我们再来看圆内接四边形有什么性质.
猜想:∠A与∠C, ∠B与∠D之间的关系为∠A+ ∠C=180 ,∠B+ ∠D=180
如图,四边形ABCD是⊙O的内接四边形,那么其相对的两个内角之间是什么关系?请你证明这个结论.
证明:连接OB,OD
在⊙O中,∠A所对的弧为BCD,∠C所对的弧为BAD.
)
)
又∵BCD与BCD所对的圆心角的度数之和为360°,
同理:∠B+∠D=180°.
得出结论:圆内接四边形对角互补.
几何语言:
∵四边形ABCD内接于⊙O
∴∠A+∠C=180°,∠B+∠D=180°
)
)
典例精讲
合作探究
例、求证:圆内接四边形的任何一个外角都等于它的内对角.
已知:如图,四边形 ABCD是⊙O的内接四边形.
求证:∠DCE=∠A.
证明:∵∠DCE+∠BCD=180°,
又∵∠A+∠BCD=180°,
∴∠DCE=∠A.
类似的:∠MBC=∠ADC
∠ADF=∠ABC
外角
内对角
F
M
归纳概念
合作探究
圆周角
圆周角定理的推论
圆内接四边形
圆内接四边形的对角互补.
推论一:同弧或等弧所对的圆周角相等.
推论二:同弧或等弧所对的圆周角相等.半圆(或直径)所对的圆周角是直角,90°的圆周角所对的弦是直径.
课堂练习
1.如图 ,四边形 ABCD 是圆内接四边形,点 E 是BC 延长线上一点,若∠BAD=105°,则∠DCE 的大小是( )
A.115° B.105° C.100° D.95°
B
2.如图 ,点A,B,C,D,E 五等分圆,则∠A+∠B+∠C+∠D+∠E=( )
A.180° B.150° C.135° D.120°
A
3.如图,点B,C,D在⊙O上,若∠BCD=130°,则∠BOD的度数是 .
1000
4.如图,已知四边形 ABCD 内接于⊙O,∠BOD =80°,求∠BAD 和∠BCD 的度数.
解:∵∠BOD=80°
∴∠BAD=40°.
又∵ABCD是圆的内接四边形,
∴∠BAD+∠BCD=180°,
∴∠BCD=140°.
5.如图,在⊙O的内接四边形ABCD中,∠BCD=120°,CA平分∠BCD.
(1)求证:△ABD是等边三角形;
(2)若BD=3,求⊙O的半径.
解:(1)∵∠BCD=120°,CA平分∠BCD,
∴∠ACD=∠ACB=60°,
由圆周角定理得,∠ADB=∠ACB=60°,∠ABD=∠ACD=60°,
∴△ABD是等边三角形;
∴⊙O的半径为
(2)连接OB、OD,作OH⊥BD于H,
则DH= BD= ,
∠BOD=2∠BAD=120°,
∴∠DOH=60°,
在Rt△ODH中,OD=
课堂总结
圆周角
圆内接四边形
圆内接四边形的对角互补.
作业布置
教材课后配套作业题。
谢谢
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
兼职招聘:
https://www.21cnjy.com/recruitment/home/admin
同课章节目录
