【核心素养目标】24.1.4.1圆周角(2) 教案
文档属性
| 名称 | 【核心素养目标】24.1.4.1圆周角(2) 教案 |

|
|
| 格式 | zip | ||
| 文件大小 | 1.3MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-07-10 21:07:16 | ||
图片预览

文档简介
中小学教育资源及组卷应用平台
24.1.4.1圆周角(2)教学设计
课题 24.1.4.1圆周角(2) 单元 第24单元 学科 数学 年级 九年级(上)
教材分析 在圆周角定理的推论的发现过程中,不断变化图形,树立运动变化和对立统一的辩证证唯物主义观点.
核心素养分析 通过圆周角定理的实际应用,发现圆内接四边形的对角互补的推论,进一步发展合情推理和演绎推理能力,感悟从特殊到一般、化一般为特殊的数学思想.
学习目标 1.了解并证明圆周角定理的推论:圆内接四边形的对角互补. 2.能应用圆周角定理及其推论解决问题.
重点 圆内接四边形的性质定理
难点 圆内接四边形性质定理的准确、灵活应用.
教学过程
教学环节 教师活动 学生活动 设计意图
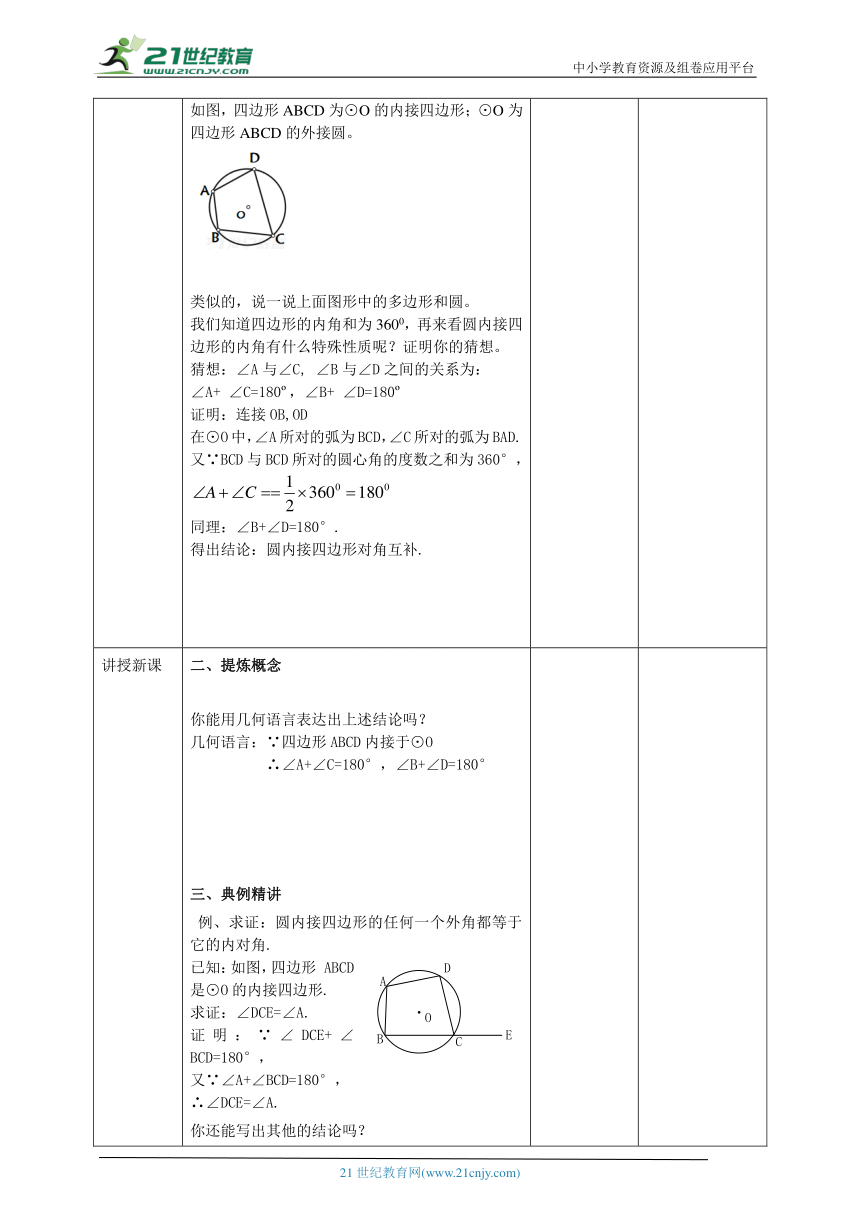
导入新课 一、创设情景,引出课题 你能说出下列多边形的名称吗?说一说,现在的多边形和圆有什么样的特殊位置关系?你能给这类图形命个名吗?定义:如果一个四边形的所有顶点都在同一个圆上,这个多边形叫做圆内接四边形.这个圆叫做这个四边形的外接圆.如图,四边形ABCD为⊙O的内接四边形;⊙O为四边形ABCD的外接圆。 类似的,说一说上面图形中的多边形和圆。我们知道四边形的内角和为3600,再来看圆内接四边形的内角有什么特殊性质呢?证明你的猜想。猜想:∠A与∠C, ∠B与∠D之间的关系为:∠A+ ∠C=180 ,∠B+ ∠D=180 证明:连接OB,OD在⊙O中,∠A所对的弧为BCD,∠C所对的弧为BAD.又∵BCD与BCD所对的圆心角的度数之和为360°,同理:∠B+∠D=180°. 得出结论:圆内接四边形对角互补. 思考自议
讲授新课 二、提炼概念你能用几何语言表达出上述结论吗?几何语言:∵四边形ABCD内接于⊙O ∴∠A+∠C=180°,∠B+∠D=180°三、典例精讲 例、求证:圆内接四边形的任何一个外角都等于它的内对角.已知:如图,四边形 ABCD是⊙O的内接四边形.求证:∠DCE=∠A.证明:∵∠DCE+∠BCD=180°,又∵∠A+∠BCD=180°,∴∠DCE=∠A.你还能写出其他的结论吗?
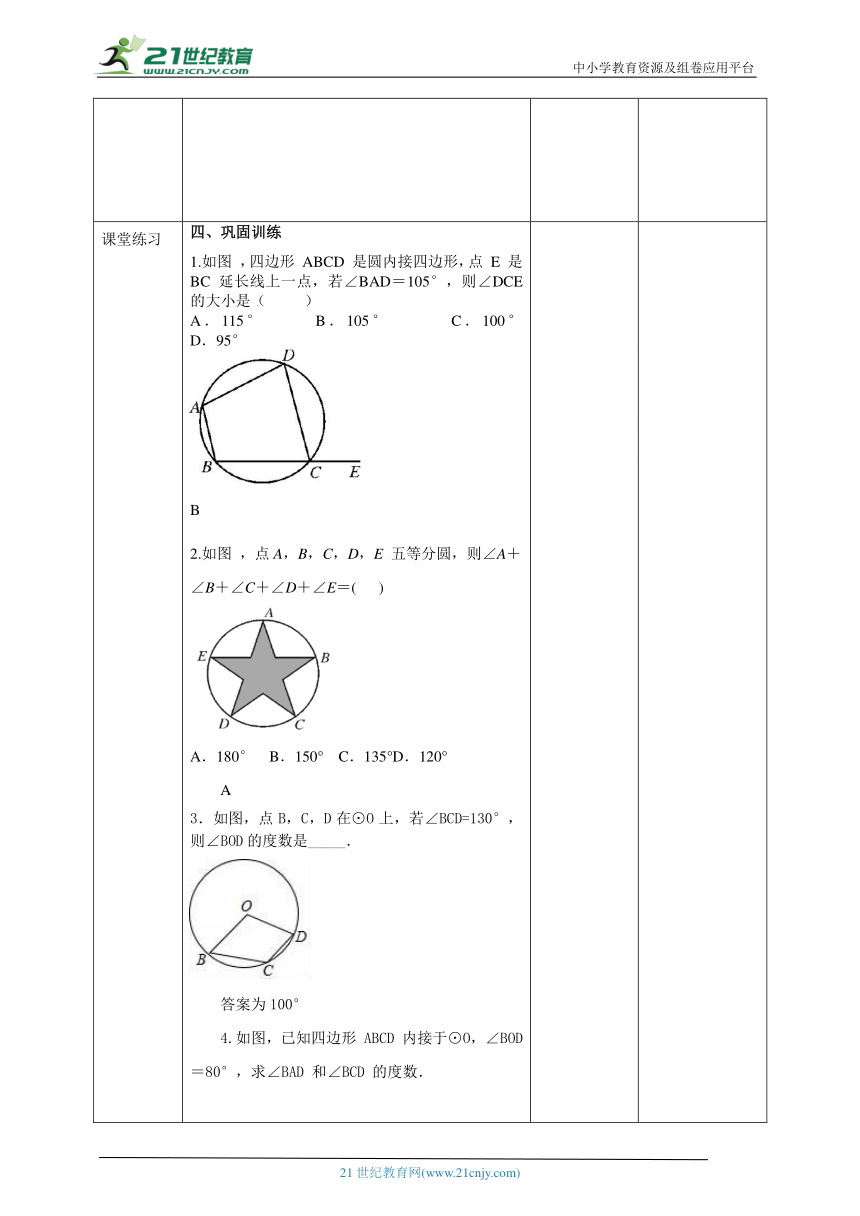
课堂练习 四、巩固训练1.如图 ,四边形 ABCD 是圆内接四边形,点 E 是BC 延长线上一点,若∠BAD=105°,则∠DCE 的大小是( )A.115° B.105° C.100° D.95°B2.如图 ,点A,B,C,D,E 五等分圆,则∠A+∠B+∠C+∠D+∠E=( ) A.180° B.150° C.135°D.120°A3.如图,点B,C,D在⊙O上,若∠BCD=130°,则∠BOD的度数是_____.答案为100°4.如图,已知四边形 ABCD 内接于⊙O,∠BOD =80°,求∠BAD 和∠BCD 的度数.解:∵∠BOD=80°∴∠BAD=40°.又∵ABCD是圆的内接四边形,∴∠BAD+∠BCD=180°,∴∠BCD=140°.5.如图,在⊙O的内接四边形ABCD中,∠BCD=120°,CA平分∠BCD.(1)求证:△ABD是等边三角形;(2)若BD=3,求⊙O的半径.解:(1)∵∠BCD=120°,CA平分∠BCD,∴∠ACD=∠ACB=60°,由圆周角定理得,∠ADB=∠ACB=60°,∠ABD=∠ACD=60°,∴△ABD是等边三角形;(2)连接OB、OD,作OH⊥BD于H,则DH=BD=,∠BOD=2∠BAD=120°,∴∠DOH=60°,在Rt△ODH中,OD=,∴⊙O的半径为.
课堂小结 本节课应掌握:圆内接四边形的定义及性质,了解从“特殊——一般”的研究问题的方法,灵活运用圆内接四边形的性质定理解决问题.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://www.21cnjy.com/" 21世纪教育网(www.21cnjy.com)
24.1.4.1圆周角(2)教学设计
课题 24.1.4.1圆周角(2) 单元 第24单元 学科 数学 年级 九年级(上)
教材分析 在圆周角定理的推论的发现过程中,不断变化图形,树立运动变化和对立统一的辩证证唯物主义观点.
核心素养分析 通过圆周角定理的实际应用,发现圆内接四边形的对角互补的推论,进一步发展合情推理和演绎推理能力,感悟从特殊到一般、化一般为特殊的数学思想.
学习目标 1.了解并证明圆周角定理的推论:圆内接四边形的对角互补. 2.能应用圆周角定理及其推论解决问题.
重点 圆内接四边形的性质定理
难点 圆内接四边形性质定理的准确、灵活应用.
教学过程
教学环节 教师活动 学生活动 设计意图
导入新课 一、创设情景,引出课题 你能说出下列多边形的名称吗?说一说,现在的多边形和圆有什么样的特殊位置关系?你能给这类图形命个名吗?定义:如果一个四边形的所有顶点都在同一个圆上,这个多边形叫做圆内接四边形.这个圆叫做这个四边形的外接圆.如图,四边形ABCD为⊙O的内接四边形;⊙O为四边形ABCD的外接圆。 类似的,说一说上面图形中的多边形和圆。我们知道四边形的内角和为3600,再来看圆内接四边形的内角有什么特殊性质呢?证明你的猜想。猜想:∠A与∠C, ∠B与∠D之间的关系为:∠A+ ∠C=180 ,∠B+ ∠D=180 证明:连接OB,OD在⊙O中,∠A所对的弧为BCD,∠C所对的弧为BAD.又∵BCD与BCD所对的圆心角的度数之和为360°,同理:∠B+∠D=180°. 得出结论:圆内接四边形对角互补. 思考自议
讲授新课 二、提炼概念你能用几何语言表达出上述结论吗?几何语言:∵四边形ABCD内接于⊙O ∴∠A+∠C=180°,∠B+∠D=180°三、典例精讲 例、求证:圆内接四边形的任何一个外角都等于它的内对角.已知:如图,四边形 ABCD是⊙O的内接四边形.求证:∠DCE=∠A.证明:∵∠DCE+∠BCD=180°,又∵∠A+∠BCD=180°,∴∠DCE=∠A.你还能写出其他的结论吗?
课堂练习 四、巩固训练1.如图 ,四边形 ABCD 是圆内接四边形,点 E 是BC 延长线上一点,若∠BAD=105°,则∠DCE 的大小是( )A.115° B.105° C.100° D.95°B2.如图 ,点A,B,C,D,E 五等分圆,则∠A+∠B+∠C+∠D+∠E=( ) A.180° B.150° C.135°D.120°A3.如图,点B,C,D在⊙O上,若∠BCD=130°,则∠BOD的度数是_____.答案为100°4.如图,已知四边形 ABCD 内接于⊙O,∠BOD =80°,求∠BAD 和∠BCD 的度数.解:∵∠BOD=80°∴∠BAD=40°.又∵ABCD是圆的内接四边形,∴∠BAD+∠BCD=180°,∴∠BCD=140°.5.如图,在⊙O的内接四边形ABCD中,∠BCD=120°,CA平分∠BCD.(1)求证:△ABD是等边三角形;(2)若BD=3,求⊙O的半径.解:(1)∵∠BCD=120°,CA平分∠BCD,∴∠ACD=∠ACB=60°,由圆周角定理得,∠ADB=∠ACB=60°,∠ABD=∠ACD=60°,∴△ABD是等边三角形;(2)连接OB、OD,作OH⊥BD于H,则DH=BD=,∠BOD=2∠BAD=120°,∴∠DOH=60°,在Rt△ODH中,OD=,∴⊙O的半径为.
课堂小结 本节课应掌握:圆内接四边形的定义及性质,了解从“特殊——一般”的研究问题的方法,灵活运用圆内接四边形的性质定理解决问题.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://www.21cnjy.com/" 21世纪教育网(www.21cnjy.com)
同课章节目录
