华师大版数学七年级上册 4.6.3余角和补角的定义和性质 课件(共36张PPT)
文档属性
| 名称 | 华师大版数学七年级上册 4.6.3余角和补角的定义和性质 课件(共36张PPT) |

|
|
| 格式 | ppt | ||
| 文件大小 | 1.2MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-07-09 11:25:19 | ||
图片预览



文档简介
(共36张PPT)
1
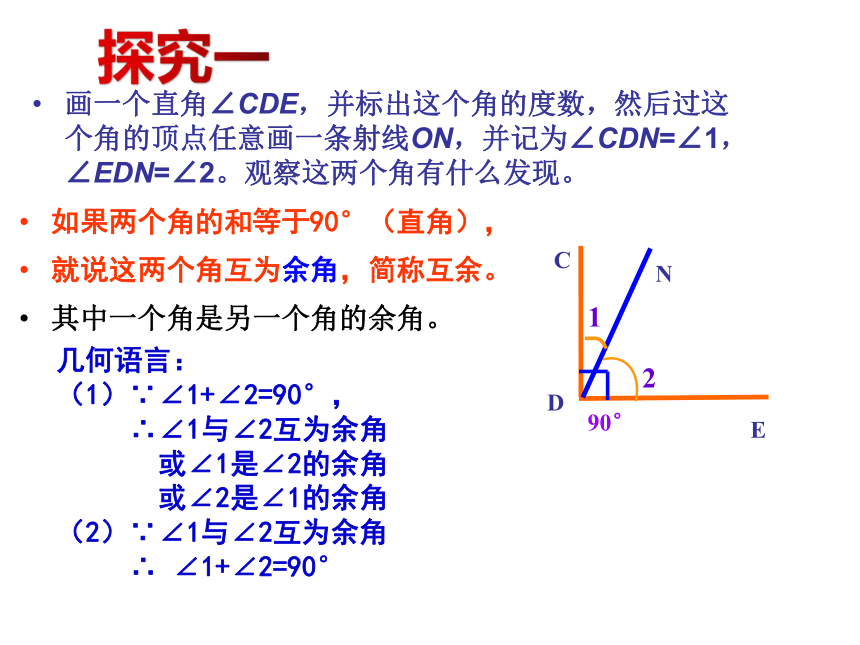
画一个直角∠CDE,并标出这个角的度数,然后过这个角的顶点任意画一条射线ON,并记为∠CDN=∠1,∠EDN=∠2。观察这两个角有什么发现。
90°
C
E
N
2
D
如果两个角的和等于90°(直角),
就说这两个角互为余角,简称互余。
其中一个角是另一个角的余角。
几何语言:
(1)∵∠1+∠2=90°,
∴∠1与∠2互为余角
或∠1是∠2的余角
或∠2是∠1的余角
(2)∵∠1与∠2互为余角
∴ ∠1+∠2=90°
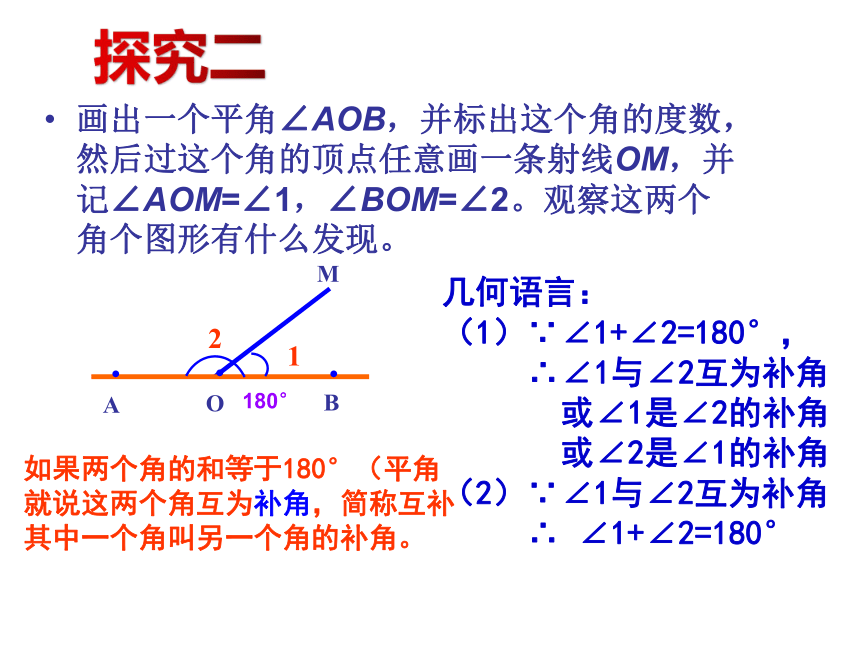
画出一个平角∠AOB,并标出这个角的度数,然后过这个角的顶点任意画一条射线OM,并记∠AOM=∠1,∠BOM=∠2。观察这两个角个图形有什么发现。
2
1
M
180°
A
B
O
·
·
·
如果两个角的和等于180°(平角
就说这两个角互为补角,简称互补
其中一个角叫另一个角的补角。
几何语言:
(1)∵∠1+∠2=180°,
∴∠1与∠2互为补角
或∠1是∠2的补角
或∠2是∠1的补角
(2)∵∠1与∠2互为补角
∴ ∠1+∠2=180°
(3) 30°的余角是_____,补角是______;若一个角的度数是x,
则它的余角的度数和补角的度数分别是__________,_________.
(1)若∠1与∠2互补,则∠1+ ∠2=________.
(2) ∠1= 180°- ∠2,则∠1与∠2的关系为___________.
180°
互为补角
60°
150°
90°- x
180°- x
1、抢答
三、反馈练习
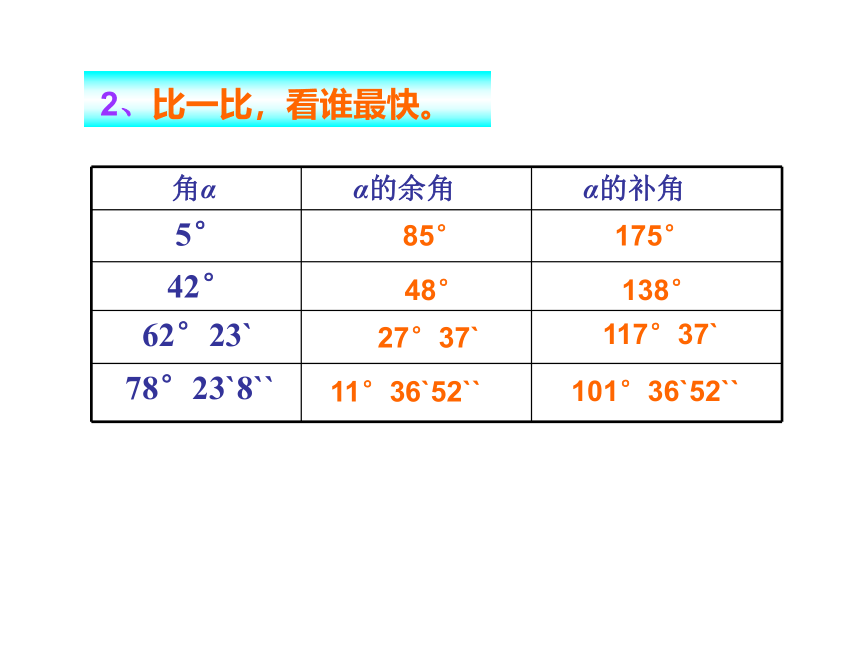
角α α的余角 α的补角
5°
42°
62°23`
78°23`8``
48°
85°
175°
138°
27°37`
117°37`
11°36`52``
101°36`52``
2、比一比,看谁最快。
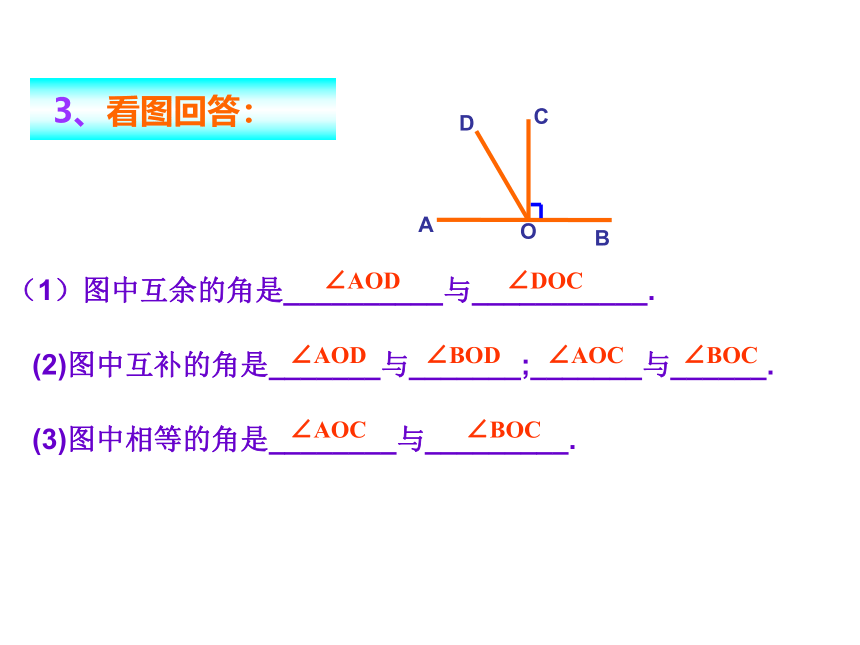
(1)图中互余的角是__________与___________.
(2)图中互补的角是_______与_______;_______与______.
(3)图中相等的角是________与_________.
A
C
O
B
D
∠AOD
∠DOC
∠AOD
∠BOD
∠AOC
∠BOC
∠AOC
∠BOC
3、看图回答:
已知∠1+∠2= 180°,∠3 +∠4= 180°。若∠1=∠3,说说∠2和∠4有什么关系?
由∠1与∠2互补,∴ ∠2= 180°- ∠1
由∠3与∠4互补,∴ ∠4= 180°- ∠3
又因为∠1=∠3, 180°- ∠1=180°- ∠3
所以∠2=∠4
推导性质
1
2
3
4
若两角之和为90°,就称这两个角互为余角。若两角之和为180°,就称这两个角互为补角。
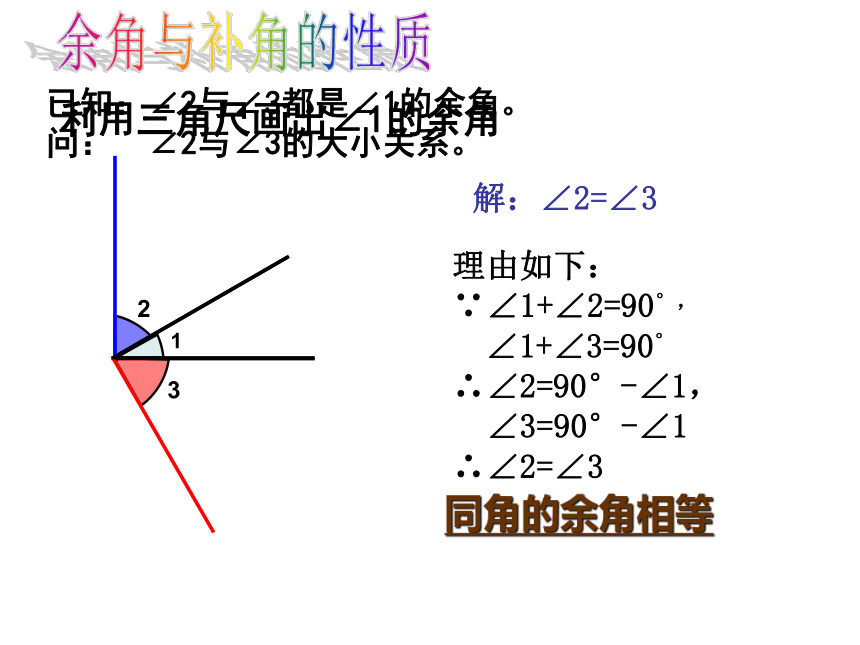
利用三角尺画出∠1的余角
1
2
3
已知:∠2与∠3都是∠1的余角。
问: ∠2与∠3的大小关系。
解:∠2=∠3
理由如下:∵∠1+∠2=90°,
∠1+∠3=90°
∴∠2=90°-∠1,
∠3=90°-∠1
∴∠2=∠3
同角的余角相等
若两角之和为90°,就称这两个角互为余角。若两角之和为180°,就称这两个角互为补角。
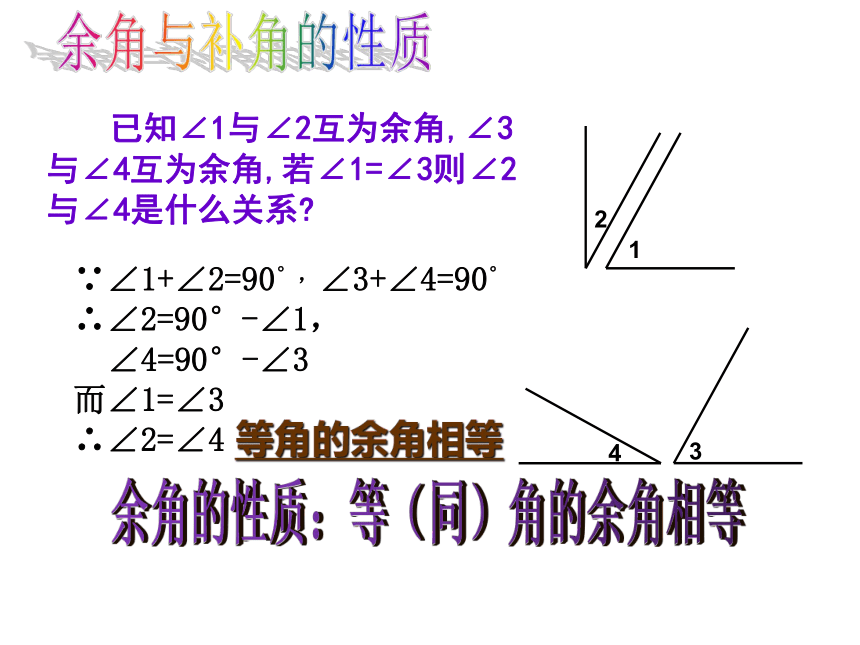
已知∠1与∠2互为余角,∠3与∠4互为余角,若∠1=∠3则∠2与∠4是什么关系
∵∠1+∠2=90°,∠3+∠4=90°
∴∠2=90°-∠1,
∠4=90°-∠3
而∠1=∠3
∴∠2=∠4
等角的余角相等
1
2
3
4
若两角之和为90°,就称这两个角互为余角。若两角之和为180°,就称这两个角互为补角。
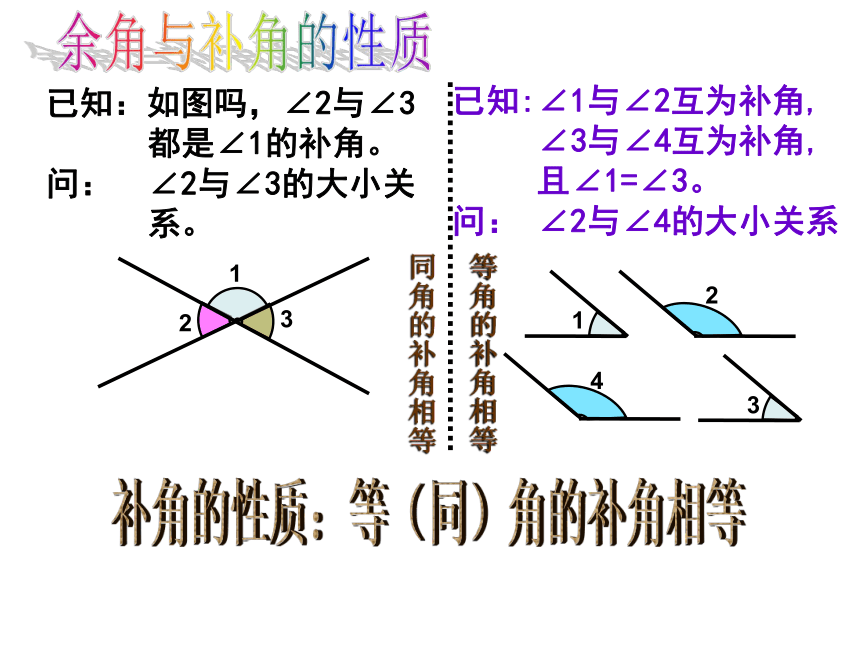
已知:如图吗,∠2与∠3
都是∠1的补角。
问: ∠2与∠3的大小关
系。
1
3
2
已知:∠1与∠2互为补角,
∠3与∠4互为补角,
且∠1=∠3。
问: ∠2与∠4的大小关系
3
4
2
1
同角的补角相等
等角的补角相等
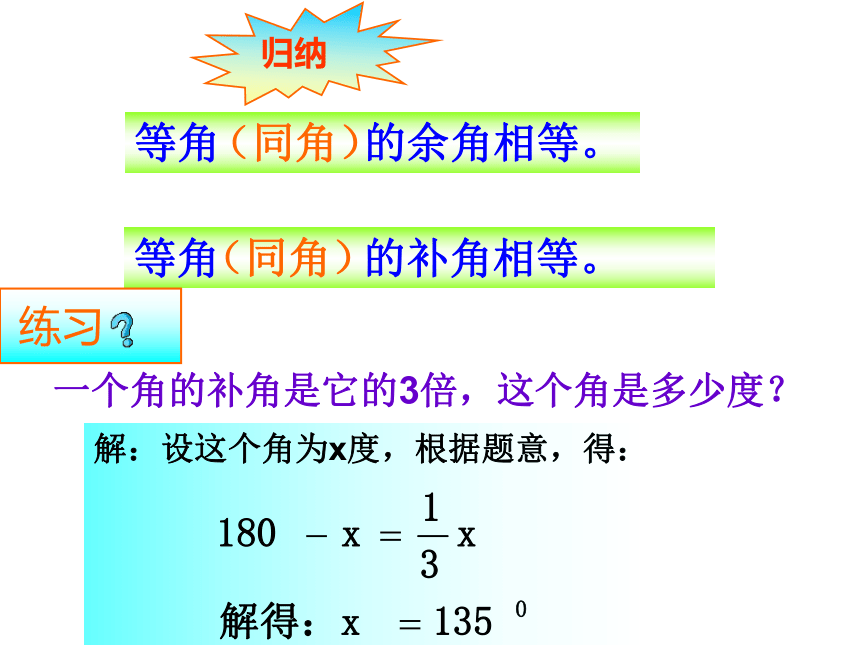
解:设这个角为x度,根据题意,得:
等角 的补角相等。
归纳
等角 的余角相等。
一个角的补角是它的3倍,这个角是多少度?
(同角)
(同角)
练习
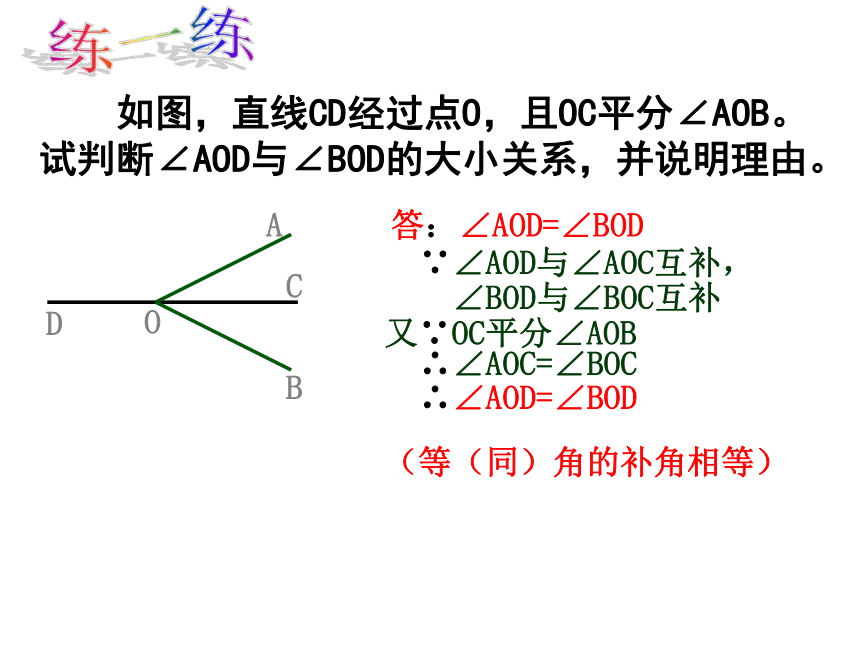
如图,直线CD经过点O,且OC平分∠AOB。试判断∠AOD与∠BOD的大小关系,并说明理由。
O
D
A
B
C
答:∠AOD=∠BOD
∵∠AOD与∠AOC互补,
∠BOD与∠BOC互补
又∵OC平分∠AOB
∴∠AOD=∠BOD
(等(同)角的补角相等)
∴∠AOC=∠BOC
等(同)角的余角相等;
等(同)角的补角相等。
如图∠AOB = 90 °
∠COD = 90 °
则∠1与∠2是什么关系?
答: ∠1 = ∠2
因为∠1+ ∠BOD = 90 °
∠2+ ∠BOD = 90 °
所以∠1 = ∠2
A
O
B
C
D
(等角的余角相等)
1
2
互为余角(互余) 互为补角(互补)
定义 如果两个锐角的和是一个直角,我们就说这两个角互为余角,简称互余。 如果两个角的和是一个平角,我们就说这两个角互为补角,简称互补。
数量关系 1+ 2=90° 1+ 2=180°
对应图形
性质 等(同)角的余角相等 等(同)角的补角相等
注意 ①互余、互补都是指两个角;
②互余、互补只与角度大小有关,与位置无关。
互余、互补是两角之间的数量关系,只与他们的度数和有关,与位置无关。
1
互余、互补概念中的角是成对出现的。
2
只有锐角才有余角。
4
注 意
角 的余角是 ,补角是
同一个锐角的补角比余角大
3
5
同角的余角(补角)相等;
等角的余角(补角)相等。
如图,已知AOB是一直线,OC是∠ AOB的平分线, ∠ DOE是直角,图中哪些角互余?哪些角互补?哪些角相等?
A
O
B
E
C
D
1
2
3
4
探索研究
1.如图,∠AOB=90°,∠COD=∠EOD=90°,C,O,E在一条直线上,且∠2=∠4,请说出∠1与∠3之间的关系?试着说明理由?
巩固应用
∵∠COD=∠EOD=90°
∴∠1+∠2=90°,∠3+∠4=90°
又∵∠2=∠4
∴∠1=∠3
(等角的余角相等)
解: (1)∠1=∠3
4
3
2
1
E
D
B
A
C
O
如图∠AOB = 90 °,∠COD = 90 °∠1与∠2是什么关系?
解: ∵∠AOB = 90 °,∠COD = 90 °
∴∠1=∠2
∴∠1+∠DOB=90°
∠2+∠DOB=90°
(同角的余角相等)
巩固练习
O
D
C
B
A
2
1
强化练习,巩固提高
(1)一个角是70 39′,求它的余角和补角.
(2)∠α的补角是它的3倍,∠α是多少度?
(3)一个角是钝角,它的一半是什么角?
它的余角是90 -70 39′=19 21′,
它的补角是180 -70 39′=109 21′.
由180 - ∠α=3 ∠α,
解得∠α=45 .
锐角
A
O
B
E
D
C
∠1=120 °, ∠1与∠2互补, ∠3与∠2互余,则∠3= .
2.O为直线AB上的一点,OD平分∠AOB,
∠COE = 90 °
则∠BOC = ,
∠COD = 。
检测
∠DOE
∠AOE
30 °
同角或等角的补角相等
同角或等角的余角相等.
如图,∠AOB=90°,∠COD=∠EOD=90°,C,O,E在一条直线上,且∠2=∠4,请说出∠1与∠3之间的关系?并试着说明理由?
300m
200m
东
南
西
北
东南
西南
西北
东北
你知道方位角吗?
东
西
北
南
O
(1)正北,正南,正西,正东,
(2)西北方向:_________
西南方向:__________
东南方向:__________
东北方向:__________
射线OD
A
B
C
D
OC
OB
OA
45°
射线OE
射线OF
射线OG
射线OH
E
G
F
H
45°
45°
45°
探究:方位角
直线AB和直线CD互相垂直,所成四个角
均为直角
2.南偏西25°
1.北偏东70°
70°
北
西
东
O
南
25°
A
B
探究:方位角
方位角是以正北、正南方向为基准,描述物体运动的方向
例1 如图,OA是表示北偏东300方向的一条射线,仿照
这条射线,画出表示下列方向的角:
(1)南偏东250 (2)北偏西600
A
东
南
西
北
300
25°
60°
例2 如图,货轮O在航行过程中,发现灯塔A在南偏东60°的方向上。同时,在它北偏东40°、南偏西10°、西北方向上又分别发现了客轮B、货轮C和海岛D.仿照表示灯塔方位的方法,画出表示客轮B、货轮C和海岛D的射线。
60°
O
A
东
南
西
北
B
40°
60°
O
A
东
南
西
北
D
C
2、如图,OA表示北偏东32°方向线, OB表示南偏东43°方向线,则∠AOB等于————。
3、A看B的方向是北偏东30°,那么B看A的方向是( )
(A)南偏东60°(B)南偏西60°
(C)南偏东30° (D)南偏西30°
A
东
北
东
北
1
2
B
甲地
乙地
如何表示乙地对甲地的方位角
1. 先找出中心点,然后画出方向指标
北
观测点
被观测点
归纳
甲地
乙地
乙地对甲地的方位角
2. 把中心点和目的地用线连接起來
北
视线
甲地
乙地
乙地对甲地的方位角
3.度量向北的射线和视线之间的角度
北
●
A
南偏西40°
南
●
东
西
北
B
40°
400
C
D
1.说出B在A的____,那么A在B的______.
北偏东400
北
东
500
南
西
A是被观测点
B是观测点
拓展应用
4、 小明从点A出发向北偏西50°方向走了3米,到达点B,小林从点A出发向南偏西40°方向走了4米,试画图确定出A、B、C三点的位置(用1厘米表示3米),并从图上求出B点到C点的实际距离。
东
南
西
北
A
500
400
B
C
4.如图,A地和B地都是海上观测站,从A地发现它
的北偏东500方向上有一艘船,同时从B地发现这
艘船在它的北偏东300方向,试在图中确定这艘
船的位置。
A
B
北
东
500
300
C
解:
则这艘船在点C处
1
画一个直角∠CDE,并标出这个角的度数,然后过这个角的顶点任意画一条射线ON,并记为∠CDN=∠1,∠EDN=∠2。观察这两个角有什么发现。
90°
C
E
N
2
D
如果两个角的和等于90°(直角),
就说这两个角互为余角,简称互余。
其中一个角是另一个角的余角。
几何语言:
(1)∵∠1+∠2=90°,
∴∠1与∠2互为余角
或∠1是∠2的余角
或∠2是∠1的余角
(2)∵∠1与∠2互为余角
∴ ∠1+∠2=90°
画出一个平角∠AOB,并标出这个角的度数,然后过这个角的顶点任意画一条射线OM,并记∠AOM=∠1,∠BOM=∠2。观察这两个角个图形有什么发现。
2
1
M
180°
A
B
O
·
·
·
如果两个角的和等于180°(平角
就说这两个角互为补角,简称互补
其中一个角叫另一个角的补角。
几何语言:
(1)∵∠1+∠2=180°,
∴∠1与∠2互为补角
或∠1是∠2的补角
或∠2是∠1的补角
(2)∵∠1与∠2互为补角
∴ ∠1+∠2=180°
(3) 30°的余角是_____,补角是______;若一个角的度数是x,
则它的余角的度数和补角的度数分别是__________,_________.
(1)若∠1与∠2互补,则∠1+ ∠2=________.
(2) ∠1= 180°- ∠2,则∠1与∠2的关系为___________.
180°
互为补角
60°
150°
90°- x
180°- x
1、抢答
三、反馈练习
角α α的余角 α的补角
5°
42°
62°23`
78°23`8``
48°
85°
175°
138°
27°37`
117°37`
11°36`52``
101°36`52``
2、比一比,看谁最快。
(1)图中互余的角是__________与___________.
(2)图中互补的角是_______与_______;_______与______.
(3)图中相等的角是________与_________.
A
C
O
B
D
∠AOD
∠DOC
∠AOD
∠BOD
∠AOC
∠BOC
∠AOC
∠BOC
3、看图回答:
已知∠1+∠2= 180°,∠3 +∠4= 180°。若∠1=∠3,说说∠2和∠4有什么关系?
由∠1与∠2互补,∴ ∠2= 180°- ∠1
由∠3与∠4互补,∴ ∠4= 180°- ∠3
又因为∠1=∠3, 180°- ∠1=180°- ∠3
所以∠2=∠4
推导性质
1
2
3
4
若两角之和为90°,就称这两个角互为余角。若两角之和为180°,就称这两个角互为补角。
利用三角尺画出∠1的余角
1
2
3
已知:∠2与∠3都是∠1的余角。
问: ∠2与∠3的大小关系。
解:∠2=∠3
理由如下:∵∠1+∠2=90°,
∠1+∠3=90°
∴∠2=90°-∠1,
∠3=90°-∠1
∴∠2=∠3
同角的余角相等
若两角之和为90°,就称这两个角互为余角。若两角之和为180°,就称这两个角互为补角。
已知∠1与∠2互为余角,∠3与∠4互为余角,若∠1=∠3则∠2与∠4是什么关系
∵∠1+∠2=90°,∠3+∠4=90°
∴∠2=90°-∠1,
∠4=90°-∠3
而∠1=∠3
∴∠2=∠4
等角的余角相等
1
2
3
4
若两角之和为90°,就称这两个角互为余角。若两角之和为180°,就称这两个角互为补角。
已知:如图吗,∠2与∠3
都是∠1的补角。
问: ∠2与∠3的大小关
系。
1
3
2
已知:∠1与∠2互为补角,
∠3与∠4互为补角,
且∠1=∠3。
问: ∠2与∠4的大小关系
3
4
2
1
同角的补角相等
等角的补角相等
解:设这个角为x度,根据题意,得:
等角 的补角相等。
归纳
等角 的余角相等。
一个角的补角是它的3倍,这个角是多少度?
(同角)
(同角)
练习
如图,直线CD经过点O,且OC平分∠AOB。试判断∠AOD与∠BOD的大小关系,并说明理由。
O
D
A
B
C
答:∠AOD=∠BOD
∵∠AOD与∠AOC互补,
∠BOD与∠BOC互补
又∵OC平分∠AOB
∴∠AOD=∠BOD
(等(同)角的补角相等)
∴∠AOC=∠BOC
等(同)角的余角相等;
等(同)角的补角相等。
如图∠AOB = 90 °
∠COD = 90 °
则∠1与∠2是什么关系?
答: ∠1 = ∠2
因为∠1+ ∠BOD = 90 °
∠2+ ∠BOD = 90 °
所以∠1 = ∠2
A
O
B
C
D
(等角的余角相等)
1
2
互为余角(互余) 互为补角(互补)
定义 如果两个锐角的和是一个直角,我们就说这两个角互为余角,简称互余。 如果两个角的和是一个平角,我们就说这两个角互为补角,简称互补。
数量关系 1+ 2=90° 1+ 2=180°
对应图形
性质 等(同)角的余角相等 等(同)角的补角相等
注意 ①互余、互补都是指两个角;
②互余、互补只与角度大小有关,与位置无关。
互余、互补是两角之间的数量关系,只与他们的度数和有关,与位置无关。
1
互余、互补概念中的角是成对出现的。
2
只有锐角才有余角。
4
注 意
角 的余角是 ,补角是
同一个锐角的补角比余角大
3
5
同角的余角(补角)相等;
等角的余角(补角)相等。
如图,已知AOB是一直线,OC是∠ AOB的平分线, ∠ DOE是直角,图中哪些角互余?哪些角互补?哪些角相等?
A
O
B
E
C
D
1
2
3
4
探索研究
1.如图,∠AOB=90°,∠COD=∠EOD=90°,C,O,E在一条直线上,且∠2=∠4,请说出∠1与∠3之间的关系?试着说明理由?
巩固应用
∵∠COD=∠EOD=90°
∴∠1+∠2=90°,∠3+∠4=90°
又∵∠2=∠4
∴∠1=∠3
(等角的余角相等)
解: (1)∠1=∠3
4
3
2
1
E
D
B
A
C
O
如图∠AOB = 90 °,∠COD = 90 °∠1与∠2是什么关系?
解: ∵∠AOB = 90 °,∠COD = 90 °
∴∠1=∠2
∴∠1+∠DOB=90°
∠2+∠DOB=90°
(同角的余角相等)
巩固练习
O
D
C
B
A
2
1
强化练习,巩固提高
(1)一个角是70 39′,求它的余角和补角.
(2)∠α的补角是它的3倍,∠α是多少度?
(3)一个角是钝角,它的一半是什么角?
它的余角是90 -70 39′=19 21′,
它的补角是180 -70 39′=109 21′.
由180 - ∠α=3 ∠α,
解得∠α=45 .
锐角
A
O
B
E
D
C
∠1=120 °, ∠1与∠2互补, ∠3与∠2互余,则∠3= .
2.O为直线AB上的一点,OD平分∠AOB,
∠COE = 90 °
则∠BOC = ,
∠COD = 。
检测
∠DOE
∠AOE
30 °
同角或等角的补角相等
同角或等角的余角相等.
如图,∠AOB=90°,∠COD=∠EOD=90°,C,O,E在一条直线上,且∠2=∠4,请说出∠1与∠3之间的关系?并试着说明理由?
300m
200m
东
南
西
北
东南
西南
西北
东北
你知道方位角吗?
东
西
北
南
O
(1)正北,正南,正西,正东,
(2)西北方向:_________
西南方向:__________
东南方向:__________
东北方向:__________
射线OD
A
B
C
D
OC
OB
OA
45°
射线OE
射线OF
射线OG
射线OH
E
G
F
H
45°
45°
45°
探究:方位角
直线AB和直线CD互相垂直,所成四个角
均为直角
2.南偏西25°
1.北偏东70°
70°
北
西
东
O
南
25°
A
B
探究:方位角
方位角是以正北、正南方向为基准,描述物体运动的方向
例1 如图,OA是表示北偏东300方向的一条射线,仿照
这条射线,画出表示下列方向的角:
(1)南偏东250 (2)北偏西600
A
东
南
西
北
300
25°
60°
例2 如图,货轮O在航行过程中,发现灯塔A在南偏东60°的方向上。同时,在它北偏东40°、南偏西10°、西北方向上又分别发现了客轮B、货轮C和海岛D.仿照表示灯塔方位的方法,画出表示客轮B、货轮C和海岛D的射线。
60°
O
A
东
南
西
北
B
40°
60°
O
A
东
南
西
北
D
C
2、如图,OA表示北偏东32°方向线, OB表示南偏东43°方向线,则∠AOB等于————。
3、A看B的方向是北偏东30°,那么B看A的方向是( )
(A)南偏东60°(B)南偏西60°
(C)南偏东30° (D)南偏西30°
A
东
北
东
北
1
2
B
甲地
乙地
如何表示乙地对甲地的方位角
1. 先找出中心点,然后画出方向指标
北
观测点
被观测点
归纳
甲地
乙地
乙地对甲地的方位角
2. 把中心点和目的地用线连接起來
北
视线
甲地
乙地
乙地对甲地的方位角
3.度量向北的射线和视线之间的角度
北
●
A
南偏西40°
南
●
东
西
北
B
40°
400
C
D
1.说出B在A的____,那么A在B的______.
北偏东400
北
东
500
南
西
A是被观测点
B是观测点
拓展应用
4、 小明从点A出发向北偏西50°方向走了3米,到达点B,小林从点A出发向南偏西40°方向走了4米,试画图确定出A、B、C三点的位置(用1厘米表示3米),并从图上求出B点到C点的实际距离。
东
南
西
北
A
500
400
B
C
4.如图,A地和B地都是海上观测站,从A地发现它
的北偏东500方向上有一艘船,同时从B地发现这
艘船在它的北偏东300方向,试在图中确定这艘
船的位置。
A
B
北
东
500
300
C
解:
则这艘船在点C处
同课章节目录
- 第1章 走进数学世界
- 数学伴我们成长
- 人类离不开数学
- 人人都能学会数学
- 第2章 有理数
- 2.1 有理数
- 2.2 数轴
- 2.3 相反数
- 2.4 绝对值
- 2.5 有理数的大小比较
- 2.6 有理数的加法
- 2.7 有理数的减法
- 2.8 有理数加减混合运算
- 2.9 有理数的乘法
- 2.10 有理数的除法
- 2.11 有理数的乘方
- 2.12 科学记数法
- 2.13 有理数的混合运算
- 2.14 近似数
- 2.15 用计算器进行计算
- 第3章 整式的加减
- 3.1 列代数式
- 3.2 代数式的值
- 3.3 整式
- 3.4 整式的加减
- 第4章 图形的初步认识
- 4.1 生活中的立体图形
- 4.2 立体图形的视图
- 4.3 立体图形的表面展开图
- 4.4 平面图形
- 4.5 最基本的图形——点和线
- 4.6 角
- 第5章 相交线与平行线
- 5.1 相交线
- 5.2 平行线
