山东省烟台市莱州市2021-2022学年七年级下学期期末数学试题(word版含答案)
文档属性
| 名称 | 山东省烟台市莱州市2021-2022学年七年级下学期期末数学试题(word版含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 628.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 鲁教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-07-09 11:18:02 | ||
图片预览

文档简介
2021—2022学年度第二学期期未学业水平检测
七年级数学试题
注意事项:
1.本试卷分试题卷和答题卡,试题卷共4页,共3道大题,28道小题,满分120分.考试时间为120分钟.
2.写在试题卷上和答题卡的指定区战之外的答案无效.
一、选择题(本题共10个小题,每小题均给出标号为A、B、C、D的四个备选答案,其中只有一个是正确的,请将正确答案的标号涂在答题卡上)
1.牛顿曾说:“反证法是数学家最精良的武器之一”.用反证法证明“在中,若,则”时,应先假设( )
A. B. C. D.
2.已知a,b,c为的三条边,满足下列条件的三角形不是直角三角形的是( )
A. B.
C. D.
3.有下列事件:①367人中必有2人的生日相同;②抛掷一只均匀的骰子两次,期上一面的点数之和一定不小于2;③在标准大气压下,温度低于时冰融化;④如果a,b为实数,那么.其中是必然事件的有( )
A.1个 B.2个 C.3个 D.4个
4.下列说法正确的是( )
A.全等三角形是指形状相同的三角形
B.全等三角形是指面积相等的两个三角形
C.全等三角形的周长和面积相等
D.所有等边三角形是全等三角形
5.如图,与的边相交,则与的大小关系为( )
A. B.
C. D.大小关系取决于的度数
6.如果不等式的正整数解为1,2,3,则m的取值范围是( )
A. B. C. D.
7.某种商品的进价为500元,出售时标价为750元,由于换季,商店准备打折销售,但要保特利润不低于,那么至多打( )
A.6折 B.7折 C.8折 D.9折
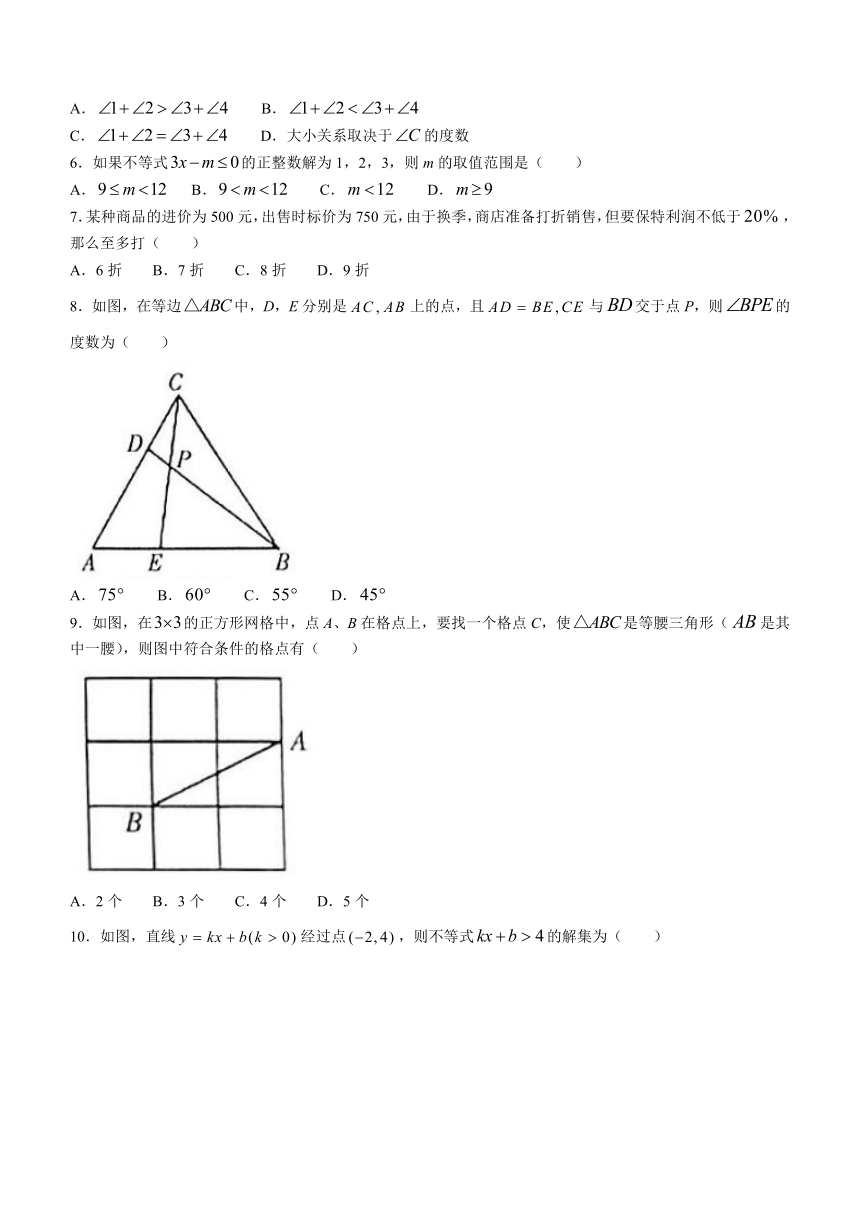
8.如图,在等边中,D,E分别是上的点,且与交于点P,则的度数为( )
A. B. C. D.
9.如图,在的正方形网格中,点A、B在格点上,要找一个格点C,使是等腰三角形(是其中一腰),则图中符合条件的格点有( )
A.2个 B.3个 C.4个 D.5个
10.如图,直线经过点,则不等式的解集为( )
A. B. C. D.
二、填空题(本题共10个小题)
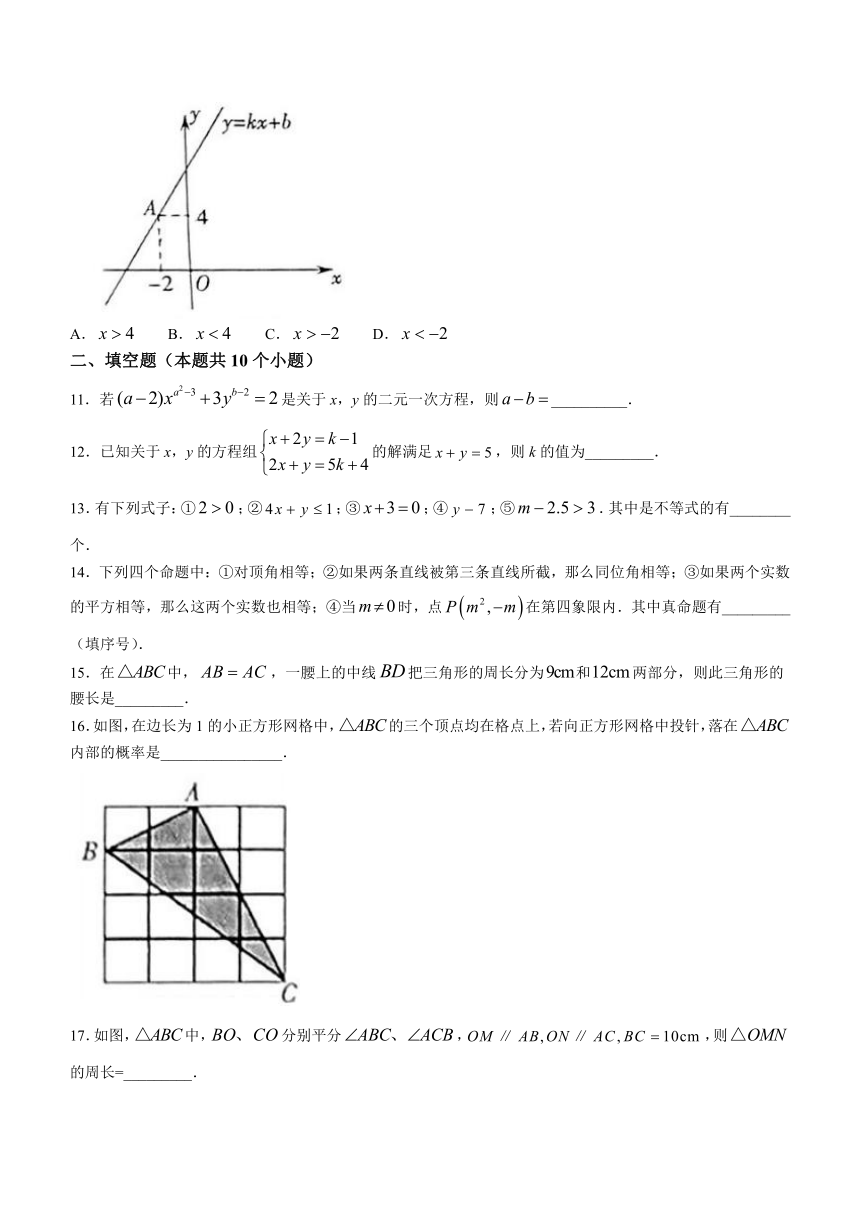
11.若是关于x,y的二元一次方程,则__________.
12.已知关于x,y的方程组的解满足,则k的值为_________.
13.有下列式子:①;②;③;④;⑤.其中是不等式的有________个.
14.下列四个命题中:①对顶角相等;②如果两条直线被第三条直线所截,那么同位角相等;③如果两个实数的平方相等,那么这两个实数也相等;④当时,点在第四象限内.其中真命题有_________(填序号).
15.在中,,一腰上的中线把三角形的周长分为和两部分,则此三角形的腰长是_________.
16.如图,在边长为1的小正方形网格中,的三个顶点均在格点上,若向正方形网格中投针,落在内部的概率是________________.
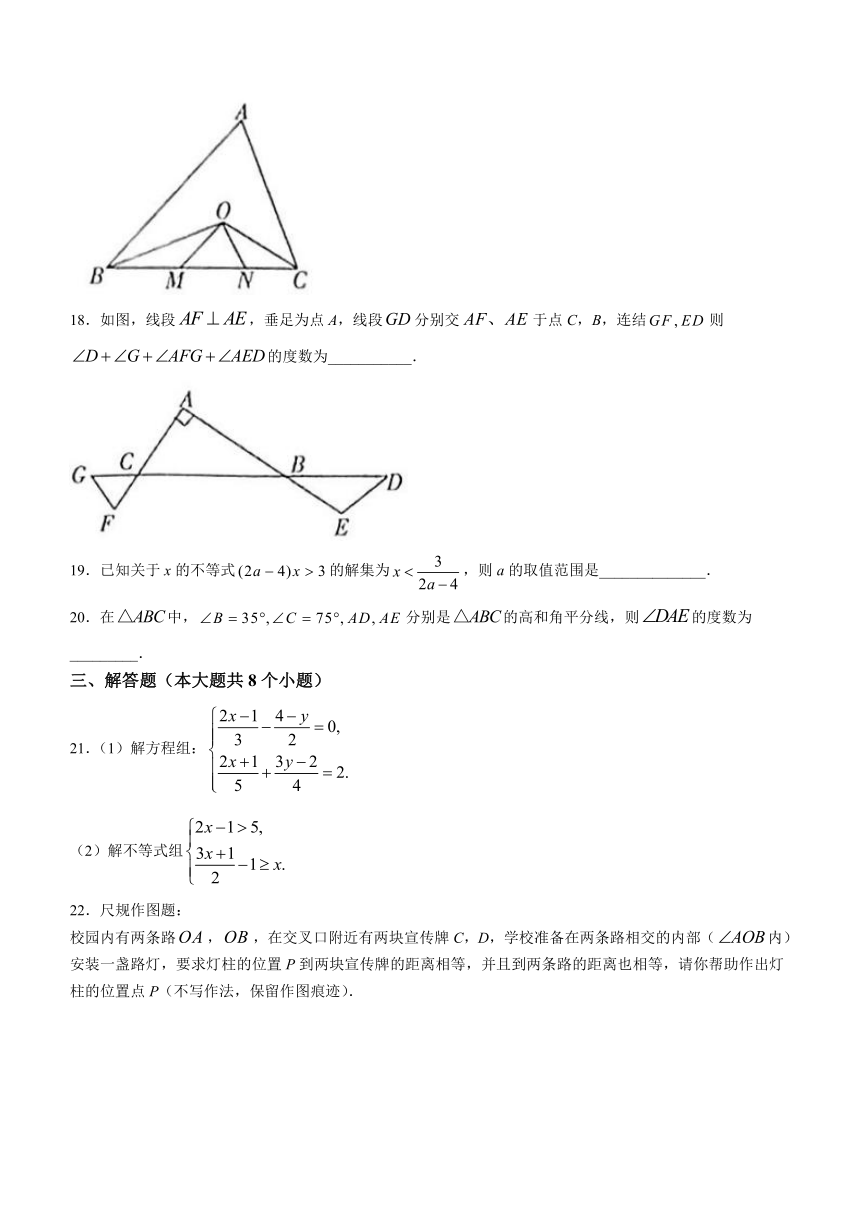
17.如图,中,分别平分,,则的周长=_________.
18.如图,线段,垂足为点A,线段分别交于点C,B,连结则的度数为___________.
19.已知关于x的不等式的解集为,则a的取值范围是______________.
20.在中,分别是的高和角平分线,则的度数为_________.
三、解答题(本大题共8个小题)
21.(1)解方程组:
(2)解不等式组
22.尺规作图题:
校园内有两条路,,在交叉口附近有两块宣传牌C,D,学校准备在两条路相交的内部(内)安装一盏路灯,要求灯柱的位置P到两块宣传牌的距离相等,并且到两条路的距离也相等,请你帮助作出灯柱的位置点P(不写作法,保留作图痕迹).
23.在一个不透明的口袋里装有4个白球和6个红球,它们除颜色外完全相同.
(1)事件“从口袋里随机摸出一个球是绿球”发生的概率是________________;
(2)事件“从口袋里随机摸出一个球是红球”发生的概率是________________;
(3)从口袋里取走x个红球后,再放人x个白球,并充分摇匀.若随机摸出白球的概率是,求x的值.
24.如图,已知中,过点B作的平分线的垂线,垂足为D,作交于E.
求证:.
25.如图所示,已知中,,E,D,F分别在和边上,且,过D作于G.
求证:.
26.设一次函数.
(1)若函数的图象与y轴交于点,求函数的表达式.
(2)若函数图象经过第一、二、三象限,求k的取值范围.
27.某工艺品店购进A,B两种工艺品,已知这两种工艺品的单价之和为200元,购进2个A种工艺品和3个B种工艺品需花费520元.求A,B两种工艺品的单价.
28.如图,C为线段上一点,,都是等边三角形,交于点E,交于点F,连接.
求证:是等边三角形.
2021-2022学年度第二学期期末学业水平检测
七年级数学试题参考答案及评分建议
一、选择题(每小题3分,满分30分)
题号 1 2 3 4 5 6 7 8 9 10
答案 D C C C C A C B D C
二、填空题(每小题3分,满分30分)
11. -5 12. 2 13. 3 14. ① 15.6cm或8cm
16. 17. 10cm 18. 270° 19. a<2 20. 20°
三、解答题(满分60分)
21.(满分8分)
(1)解:整理得
①×2,得 8x+6y=28. ③
②-③,得 9y=18,
y=2.………………………………………2分
把y=2代入①,得 4x+3×2=14,
x=2.………………………………………3分
所以原方程组的解是…………………………………………4分
解:
解不等式①,得
x>3.………………………………………1分
解不等式②,得
x≥1.………………………………………2分
在同一条数轴上表示不等式①②的解集,如图
所以,原不等式组的解集为 x>3.…………………………………4分
22.(满分6分)
(图略)
23. (满分6分)
(1)0 (2) (每小题1分)
(3)解:由题意得 .……………………………………2分
解得 x=4.…………………………………………………………4分
(满分7分)
证明:∵AD平分∠BAC,
∴∠BAD=∠CAD.………………1分
∵DE∥AC,
∴∠EDA=∠CAD.………………2分
∴∠BAD=∠EDA,
∴AE=ED. ………………………4分
∵AD⊥BD,
∴∠BAD+∠ABD=90°,
∠ADE+∠BDE=90°.
∴∠ABD=∠BDE,
∴BE=ED.………………………………………………………………6分
∴AE=BE.………………………………………………………………7分
25.(满分8分)
证明:连接DE,DF.……………………1分
∵AB=AC,
∴∠B=∠C. ……………………………3分
∵BE=CD,BD=CF,
∴△EBD≌△DCF(SAS).……………5分
∴DE=DF.………………………………………………………………6分
∵DG⊥EF,
∴EG=EF. …………………………………………………………8分
26.(满分7分)
解:(1)∵函数y1的图象与y轴交于点(0,﹣3),
∴﹣3=(k﹣1)×0+5﹣2k, …………………………………………1分
解得k=4. ……………………………………………………………2分
∴函数y1的表达式为:y1=3x﹣3; …………………………………3分
(2)∵函数y2图象经过第一,二,三象限,
∴……………………………………………………………2分
解这个不等式组,得 ﹣1<k<.………………………………3分
即k的取值范围是﹣1<k<. ………………………………………4分
27.(满分8分)
解:(1)设A,B两种工艺品的单价分别为x元、 y元,依题意得 ………………………4分
②×2,得 2x+2y=400. ③
②-③,得 y=120. …………………………………………………6分
将y=120代入①,得 x=80. ……………………………………7分
所以A,B两种工艺品的单价分别为80元、 120元. ……………8分
28.(满分10分)
证明:∵△ACM,△CBN是等边三角形,
∴AC=MC,BC=NC,
∠ACM=∠NCB=60°. ……2分
∴∠MCN=180°-∠ACM-∠NCB
=180°-60°-60°=60°. ………3分
∴∠ACN=∠MCB=120°. …4分
∴△ACN≌△MCB(SAS).…………………………………………5分
∴∠CAN=∠CMB. ……………………………………………………6分
∵∠ACE=∠MCF,AC=MC,
∴△ACE≌△MCF(ASA). …………………………………………8分
∴CE=CF. ………………………………………………………………9分
又∵∠ECF=60°,
∴△CEF为等边三角形. ……………………………………………10分
七年级数学试题
注意事项:
1.本试卷分试题卷和答题卡,试题卷共4页,共3道大题,28道小题,满分120分.考试时间为120分钟.
2.写在试题卷上和答题卡的指定区战之外的答案无效.
一、选择题(本题共10个小题,每小题均给出标号为A、B、C、D的四个备选答案,其中只有一个是正确的,请将正确答案的标号涂在答题卡上)
1.牛顿曾说:“反证法是数学家最精良的武器之一”.用反证法证明“在中,若,则”时,应先假设( )
A. B. C. D.
2.已知a,b,c为的三条边,满足下列条件的三角形不是直角三角形的是( )
A. B.
C. D.
3.有下列事件:①367人中必有2人的生日相同;②抛掷一只均匀的骰子两次,期上一面的点数之和一定不小于2;③在标准大气压下,温度低于时冰融化;④如果a,b为实数,那么.其中是必然事件的有( )
A.1个 B.2个 C.3个 D.4个
4.下列说法正确的是( )
A.全等三角形是指形状相同的三角形
B.全等三角形是指面积相等的两个三角形
C.全等三角形的周长和面积相等
D.所有等边三角形是全等三角形
5.如图,与的边相交,则与的大小关系为( )
A. B.
C. D.大小关系取决于的度数
6.如果不等式的正整数解为1,2,3,则m的取值范围是( )
A. B. C. D.
7.某种商品的进价为500元,出售时标价为750元,由于换季,商店准备打折销售,但要保特利润不低于,那么至多打( )
A.6折 B.7折 C.8折 D.9折
8.如图,在等边中,D,E分别是上的点,且与交于点P,则的度数为( )
A. B. C. D.
9.如图,在的正方形网格中,点A、B在格点上,要找一个格点C,使是等腰三角形(是其中一腰),则图中符合条件的格点有( )
A.2个 B.3个 C.4个 D.5个
10.如图,直线经过点,则不等式的解集为( )
A. B. C. D.
二、填空题(本题共10个小题)
11.若是关于x,y的二元一次方程,则__________.
12.已知关于x,y的方程组的解满足,则k的值为_________.
13.有下列式子:①;②;③;④;⑤.其中是不等式的有________个.
14.下列四个命题中:①对顶角相等;②如果两条直线被第三条直线所截,那么同位角相等;③如果两个实数的平方相等,那么这两个实数也相等;④当时,点在第四象限内.其中真命题有_________(填序号).
15.在中,,一腰上的中线把三角形的周长分为和两部分,则此三角形的腰长是_________.
16.如图,在边长为1的小正方形网格中,的三个顶点均在格点上,若向正方形网格中投针,落在内部的概率是________________.
17.如图,中,分别平分,,则的周长=_________.
18.如图,线段,垂足为点A,线段分别交于点C,B,连结则的度数为___________.
19.已知关于x的不等式的解集为,则a的取值范围是______________.
20.在中,分别是的高和角平分线,则的度数为_________.
三、解答题(本大题共8个小题)
21.(1)解方程组:
(2)解不等式组
22.尺规作图题:
校园内有两条路,,在交叉口附近有两块宣传牌C,D,学校准备在两条路相交的内部(内)安装一盏路灯,要求灯柱的位置P到两块宣传牌的距离相等,并且到两条路的距离也相等,请你帮助作出灯柱的位置点P(不写作法,保留作图痕迹).
23.在一个不透明的口袋里装有4个白球和6个红球,它们除颜色外完全相同.
(1)事件“从口袋里随机摸出一个球是绿球”发生的概率是________________;
(2)事件“从口袋里随机摸出一个球是红球”发生的概率是________________;
(3)从口袋里取走x个红球后,再放人x个白球,并充分摇匀.若随机摸出白球的概率是,求x的值.
24.如图,已知中,过点B作的平分线的垂线,垂足为D,作交于E.
求证:.
25.如图所示,已知中,,E,D,F分别在和边上,且,过D作于G.
求证:.
26.设一次函数.
(1)若函数的图象与y轴交于点,求函数的表达式.
(2)若函数图象经过第一、二、三象限,求k的取值范围.
27.某工艺品店购进A,B两种工艺品,已知这两种工艺品的单价之和为200元,购进2个A种工艺品和3个B种工艺品需花费520元.求A,B两种工艺品的单价.
28.如图,C为线段上一点,,都是等边三角形,交于点E,交于点F,连接.
求证:是等边三角形.
2021-2022学年度第二学期期末学业水平检测
七年级数学试题参考答案及评分建议
一、选择题(每小题3分,满分30分)
题号 1 2 3 4 5 6 7 8 9 10
答案 D C C C C A C B D C
二、填空题(每小题3分,满分30分)
11. -5 12. 2 13. 3 14. ① 15.6cm或8cm
16. 17. 10cm 18. 270° 19. a<2 20. 20°
三、解答题(满分60分)
21.(满分8分)
(1)解:整理得
①×2,得 8x+6y=28. ③
②-③,得 9y=18,
y=2.………………………………………2分
把y=2代入①,得 4x+3×2=14,
x=2.………………………………………3分
所以原方程组的解是…………………………………………4分
解:
解不等式①,得
x>3.………………………………………1分
解不等式②,得
x≥1.………………………………………2分
在同一条数轴上表示不等式①②的解集,如图
所以,原不等式组的解集为 x>3.…………………………………4分
22.(满分6分)
(图略)
23. (满分6分)
(1)0 (2) (每小题1分)
(3)解:由题意得 .……………………………………2分
解得 x=4.…………………………………………………………4分
(满分7分)
证明:∵AD平分∠BAC,
∴∠BAD=∠CAD.………………1分
∵DE∥AC,
∴∠EDA=∠CAD.………………2分
∴∠BAD=∠EDA,
∴AE=ED. ………………………4分
∵AD⊥BD,
∴∠BAD+∠ABD=90°,
∠ADE+∠BDE=90°.
∴∠ABD=∠BDE,
∴BE=ED.………………………………………………………………6分
∴AE=BE.………………………………………………………………7分
25.(满分8分)
证明:连接DE,DF.……………………1分
∵AB=AC,
∴∠B=∠C. ……………………………3分
∵BE=CD,BD=CF,
∴△EBD≌△DCF(SAS).……………5分
∴DE=DF.………………………………………………………………6分
∵DG⊥EF,
∴EG=EF. …………………………………………………………8分
26.(满分7分)
解:(1)∵函数y1的图象与y轴交于点(0,﹣3),
∴﹣3=(k﹣1)×0+5﹣2k, …………………………………………1分
解得k=4. ……………………………………………………………2分
∴函数y1的表达式为:y1=3x﹣3; …………………………………3分
(2)∵函数y2图象经过第一,二,三象限,
∴……………………………………………………………2分
解这个不等式组,得 ﹣1<k<.………………………………3分
即k的取值范围是﹣1<k<. ………………………………………4分
27.(满分8分)
解:(1)设A,B两种工艺品的单价分别为x元、 y元,依题意得 ………………………4分
②×2,得 2x+2y=400. ③
②-③,得 y=120. …………………………………………………6分
将y=120代入①,得 x=80. ……………………………………7分
所以A,B两种工艺品的单价分别为80元、 120元. ……………8分
28.(满分10分)
证明:∵△ACM,△CBN是等边三角形,
∴AC=MC,BC=NC,
∠ACM=∠NCB=60°. ……2分
∴∠MCN=180°-∠ACM-∠NCB
=180°-60°-60°=60°. ………3分
∴∠ACN=∠MCB=120°. …4分
∴△ACN≌△MCB(SAS).…………………………………………5分
∴∠CAN=∠CMB. ……………………………………………………6分
∵∠ACE=∠MCF,AC=MC,
∴△ACE≌△MCF(ASA). …………………………………………8分
∴CE=CF. ………………………………………………………………9分
又∵∠ECF=60°,
∴△CEF为等边三角形. ……………………………………………10分
同课章节目录
