人教版数学九年级上册同步提优训练:25.1.2 概率(word、含答案)
文档属性
| 名称 | 人教版数学九年级上册同步提优训练:25.1.2 概率(word、含答案) |

|
|
| 格式 | docx | ||
| 文件大小 | 292.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-07-09 16:13:28 | ||
图片预览


文档简介
25.1.2 概率
命题点 1 概率的意义
1.有人预测2024年巴黎奥运会上中国女排夺冠的概率是80%,对这个说法正确的理解应该是( )
A.中国女排一定会夺冠
B.中国女排一定不会夺冠
C.中国女排夺冠的可能性比较大
D.中国女排夺冠的可能性比较小
2.下列事件发生的概率为0的是( )
A.射击运动员只射击1次,就命中靶心
B.任取一个实数x,都有|x|≥0
C.画一个三角形,使其三边的长分别为8 cm,6 cm,2 cm
D.抛掷一枚质地均匀且六个面上分别刻有1到6的点数的正方体骰子,朝上一面的点数为6
命题点 2 利用概率公式计算事件发生的概率
3.如图,有6张扑克牌,从中随机抽取一张,牌上的数为偶数的概率是( )
A. B.
C. D.
4.掷一枚质地均匀的正方体骰子,观察向上一面的点数,与点数3相差2的概率是( )
A. B.
C. D.
5.小宝的妈妈让他从袋子里挑选一颗糖果.小宝无法看到袋子里的糖果,图是袋子里各种颜色糖果的数量,则小宝选到红色糖果的概率是( )
A. B. C. D.
6.2021杭州 某轨道列车共有3节车厢,设乘客从任意一节车厢上车的机会均等.某天甲、乙两位乘客同时乘同一列轨道列车,则甲和乙从同一节车厢上车的概率是( )
A. B. C. D.
7.2021临沂 现有4盒同一品牌的牛奶,其中2盒已过期,随机抽取2盒,至少有一盒过期的概率是( )
A. B. C. D.
8.2020绥化 在一个不透明的袋子中装有黑球m个、白球n个、红球3个,这些球除颜色外无其他差别,任意摸出一个球是红球的概率是( )
A. B.
C. D.
9.2020襄阳《易经》是中国传统文化的精髓.如图是易经的一种卦图,图中每一卦由三根线组成(线形为或),如图正北方向的卦为.从图中三根线组成的卦中任取一卦,这一卦中恰有2根和1根的概率为________.
10.一个盒中装着质地、大小、外形一模一样的x颗白色弹珠和y颗黑色弹珠,从盒中随机取出1颗弹珠,取得白色弹珠的概率是.若再往盒中放12颗同样的白色弹珠,取得白色弹珠的概率是,则原来盒中有白色弹珠________颗.
命题点 3 几何概率
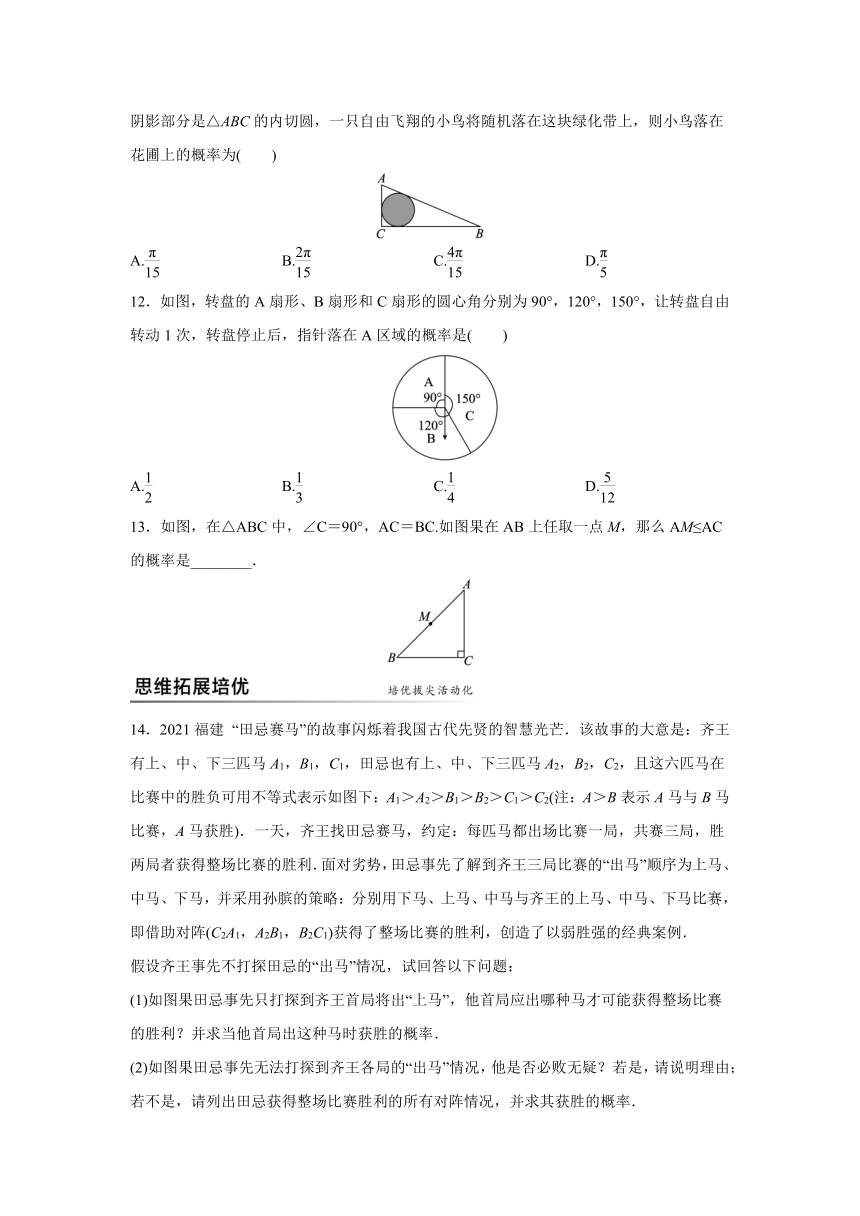
11.如图,△ABC是一块绿化带,将阴影部分修建为花圃,已知AB=13,AC=5,BC=12,阴影部分是△ABC的内切圆,一只自由飞翔的小鸟将随机落在这块绿化带上,则小鸟落在花圃上的概率为( )
A. B. C. D.
12.如图,转盘的A扇形、B扇形和C扇形的圆心角分别为90°,120°,150°,让转盘自由转动1次,转盘停止后,指针落在A区域的概率是( )
A. B. C. D.
13.如图,在△ABC中,∠C=90°,AC=BC.如图果在AB上任取一点M,那么AM≤AC的概率是________.
14.2021福建 “田忌赛马”的故事闪烁着我国古代先贤的智慧光芒.该故事的大意是:齐王有上、中、下三匹马A1,B1,C1,田忌也有上、中、下三匹马A2,B2,C2,且这六匹马在比赛中的胜负可用不等式表示如图下:A1>A2>B1>B2>C1>C2(注:A>B表示A马与B马比赛,A马获胜).一天,齐王找田忌赛马,约定:每匹马都出场比赛一局,共赛三局,胜两局者获得整场比赛的胜利.面对劣势,田忌事先了解到齐王三局比赛的“出马”顺序为上马、中马、下马,并采用孙膑的策略:分别用下马、上马、中马与齐王的上马、中马、下马比赛,即借助对阵(C2A1,A2B1,B2C1)获得了整场比赛的胜利,创造了以弱胜强的经典案例.
假设齐王事先不打探田忌的“出马”情况,试回答以下问题:
(1)如图果田忌事先只打探到齐王首局将出“上马”,他首局应出哪种马才可能获得整场比赛的胜利?并求当他首局出这种马时获胜的概率.
(2)如图果田忌事先无法打探到齐王各局的“出马”情况,他是否必败无疑?若是,请说明理由;若不是,请列出田忌获得整场比赛胜利的所有对阵情况,并求其获胜的概率.
方法点拨(2题) 概率为0的事件是不可能事件. 解题突破(4题) 与点数3相差2的点数有几种情况? 方法点拨(8题) 口袋里有n个球,其中有m个某种颜色的球,随机摸出1个,则摸到这种颜色球的概率为.
法点拨(11题) 直角三角形内切圆的半径等于两直角边长的和减去斜边长的差的一半.
答案
1.C
2.C 选项A是随机事件,概率在0到1之间;选项B是一个必然事件,概率为1;选项C是一个不可能事件,概率为0;选项D是一个随机事件,概率为.
3.D
4.B 掷一枚质地均匀的正方体骰子,向上一面的点数一共有6种等可能结果,分别为1,2,3,4,5,6,其中与点数3相差2的点数为1,5,所以P(与点数3相差2)==.
5.C 由条形图知,共有糖果6+5+3+3+2+4+2+5=30(颗),其中红色糖果有6颗,
∴小宝选到红色糖果的概率是=.
6.C
7.D 把2盒不过期的牛奶记为A,B,2盒已过期的牛奶记为C,D.
画树状图如图:
共有12种等可能的结果,至少有一盒过期的结果有10种,
∴至少有一盒过期的概率为=.
8.B 9.
10.4 ∵第一次取得白色弹珠的概率是,
∴=,解得y=2x.
∵再往盒中放12颗同样的白色弹珠,取得白色弹珠的概率是,∴=,
将y=2x代入,
解得x=4,y=8.
经检验,x=4,y=8均是分式方程的根且符合题意.
11.B ∵AB=13,BC=12,AC=5,
∴AB2=BC2+AC2,
∴△ABC为直角三角形,且∠ACB=90°,
∴△ABC的内切圆半径==2.
∵S△ABC=AC·BC=×5×12=30,S圆=4π,
∴小鸟落在花圃上的概率==.
12.C ∵转盘的A扇形、B扇形和C扇形的圆心角分别为90°,120°,150°,
∴让转盘自由转动1次,转盘停止后指针落在A区域的概率为=.
故选C.
13. 在等腰直角三角形ABC中,设边AC的长为1,则边AB的长为.在AB上取点D,使AD=1,则点M在线段AD上时,才满足条件.故在AB上任取一点M,AM≤AC的概率为=.
14.解:(1)田忌首局应出“下马”才可能在整场比赛中获胜.
此时,比赛的所有可能对阵为(C2A1,A2B1,B2C1),(C2A1,B2C1,A2B1),(C2A1,B2B1,A2C1),(C2A1,A2C1,B2B1),共四种,
其中田忌获胜的对阵有(C2A1,A2B1,B2C1),(C2A1,B2C1,A2B1),共两种,
故此时田忌获胜的概率为=.
(2)不是.
齐王的出马顺序为A1,B1,C1时,田忌获胜的对阵是(C2A1,A2B1,B2C1),
齐王的出马顺序为A1,C1,B1时,田忌获胜的对阵是(C2A1,B2C1,A2B1),
齐王的出马顺序为B1,A1,C1时,田忌获胜的对阵是(A2B1,C2A1,B2C1),
齐王的出马顺序为B1,C1,A1时,田忌获胜的对阵是(A2B1,B2C1,C2A1),
齐王的出马顺序为C1,A1,B1时,田忌获胜的对阵是(B2C1,C2A1,A2B1),
齐王的出马顺序为C1,B1,A1时,田忌获胜的对阵是(B2C1,A2B1,C2A1),
综上所述,田忌获胜的所有对阵是(C2A1,A2B1,B2C1),(C2A1,B2C1,A2B1),(A2B1,C2A1,B2C1),(A2B1,B2C1,C2A1),(B2C1,C2A1,A2B1),(B2C1,A2B1,C2A1).
齐王的出场顺序为A1,B1,C1时,比赛的所有可能对阵是(A2A1,B2B1,C2C1),(A2A1,C2B1,B2C1),(B2A1,A2B1,C2C1),(B2A1,C2B1,A2C1),(C2A1,A2B1,B2C1),(C2A1,B2B1,A2C1).共6种,同理,齐王的其他各种出马顺序,也都分别有相应的6种可能对阵,所以,此时田忌获胜的概率为=.
命题点 1 概率的意义
1.有人预测2024年巴黎奥运会上中国女排夺冠的概率是80%,对这个说法正确的理解应该是( )
A.中国女排一定会夺冠
B.中国女排一定不会夺冠
C.中国女排夺冠的可能性比较大
D.中国女排夺冠的可能性比较小
2.下列事件发生的概率为0的是( )
A.射击运动员只射击1次,就命中靶心
B.任取一个实数x,都有|x|≥0
C.画一个三角形,使其三边的长分别为8 cm,6 cm,2 cm
D.抛掷一枚质地均匀且六个面上分别刻有1到6的点数的正方体骰子,朝上一面的点数为6
命题点 2 利用概率公式计算事件发生的概率
3.如图,有6张扑克牌,从中随机抽取一张,牌上的数为偶数的概率是( )
A. B.
C. D.
4.掷一枚质地均匀的正方体骰子,观察向上一面的点数,与点数3相差2的概率是( )
A. B.
C. D.
5.小宝的妈妈让他从袋子里挑选一颗糖果.小宝无法看到袋子里的糖果,图是袋子里各种颜色糖果的数量,则小宝选到红色糖果的概率是( )
A. B. C. D.
6.2021杭州 某轨道列车共有3节车厢,设乘客从任意一节车厢上车的机会均等.某天甲、乙两位乘客同时乘同一列轨道列车,则甲和乙从同一节车厢上车的概率是( )
A. B. C. D.
7.2021临沂 现有4盒同一品牌的牛奶,其中2盒已过期,随机抽取2盒,至少有一盒过期的概率是( )
A. B. C. D.
8.2020绥化 在一个不透明的袋子中装有黑球m个、白球n个、红球3个,这些球除颜色外无其他差别,任意摸出一个球是红球的概率是( )
A. B.
C. D.
9.2020襄阳《易经》是中国传统文化的精髓.如图是易经的一种卦图,图中每一卦由三根线组成(线形为或),如图正北方向的卦为.从图中三根线组成的卦中任取一卦,这一卦中恰有2根和1根的概率为________.
10.一个盒中装着质地、大小、外形一模一样的x颗白色弹珠和y颗黑色弹珠,从盒中随机取出1颗弹珠,取得白色弹珠的概率是.若再往盒中放12颗同样的白色弹珠,取得白色弹珠的概率是,则原来盒中有白色弹珠________颗.
命题点 3 几何概率
11.如图,△ABC是一块绿化带,将阴影部分修建为花圃,已知AB=13,AC=5,BC=12,阴影部分是△ABC的内切圆,一只自由飞翔的小鸟将随机落在这块绿化带上,则小鸟落在花圃上的概率为( )
A. B. C. D.
12.如图,转盘的A扇形、B扇形和C扇形的圆心角分别为90°,120°,150°,让转盘自由转动1次,转盘停止后,指针落在A区域的概率是( )
A. B. C. D.
13.如图,在△ABC中,∠C=90°,AC=BC.如图果在AB上任取一点M,那么AM≤AC的概率是________.
14.2021福建 “田忌赛马”的故事闪烁着我国古代先贤的智慧光芒.该故事的大意是:齐王有上、中、下三匹马A1,B1,C1,田忌也有上、中、下三匹马A2,B2,C2,且这六匹马在比赛中的胜负可用不等式表示如图下:A1>A2>B1>B2>C1>C2(注:A>B表示A马与B马比赛,A马获胜).一天,齐王找田忌赛马,约定:每匹马都出场比赛一局,共赛三局,胜两局者获得整场比赛的胜利.面对劣势,田忌事先了解到齐王三局比赛的“出马”顺序为上马、中马、下马,并采用孙膑的策略:分别用下马、上马、中马与齐王的上马、中马、下马比赛,即借助对阵(C2A1,A2B1,B2C1)获得了整场比赛的胜利,创造了以弱胜强的经典案例.
假设齐王事先不打探田忌的“出马”情况,试回答以下问题:
(1)如图果田忌事先只打探到齐王首局将出“上马”,他首局应出哪种马才可能获得整场比赛的胜利?并求当他首局出这种马时获胜的概率.
(2)如图果田忌事先无法打探到齐王各局的“出马”情况,他是否必败无疑?若是,请说明理由;若不是,请列出田忌获得整场比赛胜利的所有对阵情况,并求其获胜的概率.
方法点拨(2题) 概率为0的事件是不可能事件. 解题突破(4题) 与点数3相差2的点数有几种情况? 方法点拨(8题) 口袋里有n个球,其中有m个某种颜色的球,随机摸出1个,则摸到这种颜色球的概率为.
法点拨(11题) 直角三角形内切圆的半径等于两直角边长的和减去斜边长的差的一半.
答案
1.C
2.C 选项A是随机事件,概率在0到1之间;选项B是一个必然事件,概率为1;选项C是一个不可能事件,概率为0;选项D是一个随机事件,概率为.
3.D
4.B 掷一枚质地均匀的正方体骰子,向上一面的点数一共有6种等可能结果,分别为1,2,3,4,5,6,其中与点数3相差2的点数为1,5,所以P(与点数3相差2)==.
5.C 由条形图知,共有糖果6+5+3+3+2+4+2+5=30(颗),其中红色糖果有6颗,
∴小宝选到红色糖果的概率是=.
6.C
7.D 把2盒不过期的牛奶记为A,B,2盒已过期的牛奶记为C,D.
画树状图如图:
共有12种等可能的结果,至少有一盒过期的结果有10种,
∴至少有一盒过期的概率为=.
8.B 9.
10.4 ∵第一次取得白色弹珠的概率是,
∴=,解得y=2x.
∵再往盒中放12颗同样的白色弹珠,取得白色弹珠的概率是,∴=,
将y=2x代入,
解得x=4,y=8.
经检验,x=4,y=8均是分式方程的根且符合题意.
11.B ∵AB=13,BC=12,AC=5,
∴AB2=BC2+AC2,
∴△ABC为直角三角形,且∠ACB=90°,
∴△ABC的内切圆半径==2.
∵S△ABC=AC·BC=×5×12=30,S圆=4π,
∴小鸟落在花圃上的概率==.
12.C ∵转盘的A扇形、B扇形和C扇形的圆心角分别为90°,120°,150°,
∴让转盘自由转动1次,转盘停止后指针落在A区域的概率为=.
故选C.
13. 在等腰直角三角形ABC中,设边AC的长为1,则边AB的长为.在AB上取点D,使AD=1,则点M在线段AD上时,才满足条件.故在AB上任取一点M,AM≤AC的概率为=.
14.解:(1)田忌首局应出“下马”才可能在整场比赛中获胜.
此时,比赛的所有可能对阵为(C2A1,A2B1,B2C1),(C2A1,B2C1,A2B1),(C2A1,B2B1,A2C1),(C2A1,A2C1,B2B1),共四种,
其中田忌获胜的对阵有(C2A1,A2B1,B2C1),(C2A1,B2C1,A2B1),共两种,
故此时田忌获胜的概率为=.
(2)不是.
齐王的出马顺序为A1,B1,C1时,田忌获胜的对阵是(C2A1,A2B1,B2C1),
齐王的出马顺序为A1,C1,B1时,田忌获胜的对阵是(C2A1,B2C1,A2B1),
齐王的出马顺序为B1,A1,C1时,田忌获胜的对阵是(A2B1,C2A1,B2C1),
齐王的出马顺序为B1,C1,A1时,田忌获胜的对阵是(A2B1,B2C1,C2A1),
齐王的出马顺序为C1,A1,B1时,田忌获胜的对阵是(B2C1,C2A1,A2B1),
齐王的出马顺序为C1,B1,A1时,田忌获胜的对阵是(B2C1,A2B1,C2A1),
综上所述,田忌获胜的所有对阵是(C2A1,A2B1,B2C1),(C2A1,B2C1,A2B1),(A2B1,C2A1,B2C1),(A2B1,B2C1,C2A1),(B2C1,C2A1,A2B1),(B2C1,A2B1,C2A1).
齐王的出场顺序为A1,B1,C1时,比赛的所有可能对阵是(A2A1,B2B1,C2C1),(A2A1,C2B1,B2C1),(B2A1,A2B1,C2C1),(B2A1,C2B1,A2C1),(C2A1,A2B1,B2C1),(C2A1,B2B1,A2C1).共6种,同理,齐王的其他各种出马顺序,也都分别有相应的6种可能对阵,所以,此时田忌获胜的概率为=.
同课章节目录
