人教版数学九年级上册同步提优训练:24.3 正多边形和圆(word、含答案)
文档属性
| 名称 | 人教版数学九年级上册同步提优训练:24.3 正多边形和圆(word、含答案) |
|
|
| 格式 | docx | ||
| 文件大小 | 489.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-07-09 00:00:00 | ||
图片预览



文档简介
24.3 正多边形和圆
命题点 1 利用正多边形的性质进行计算
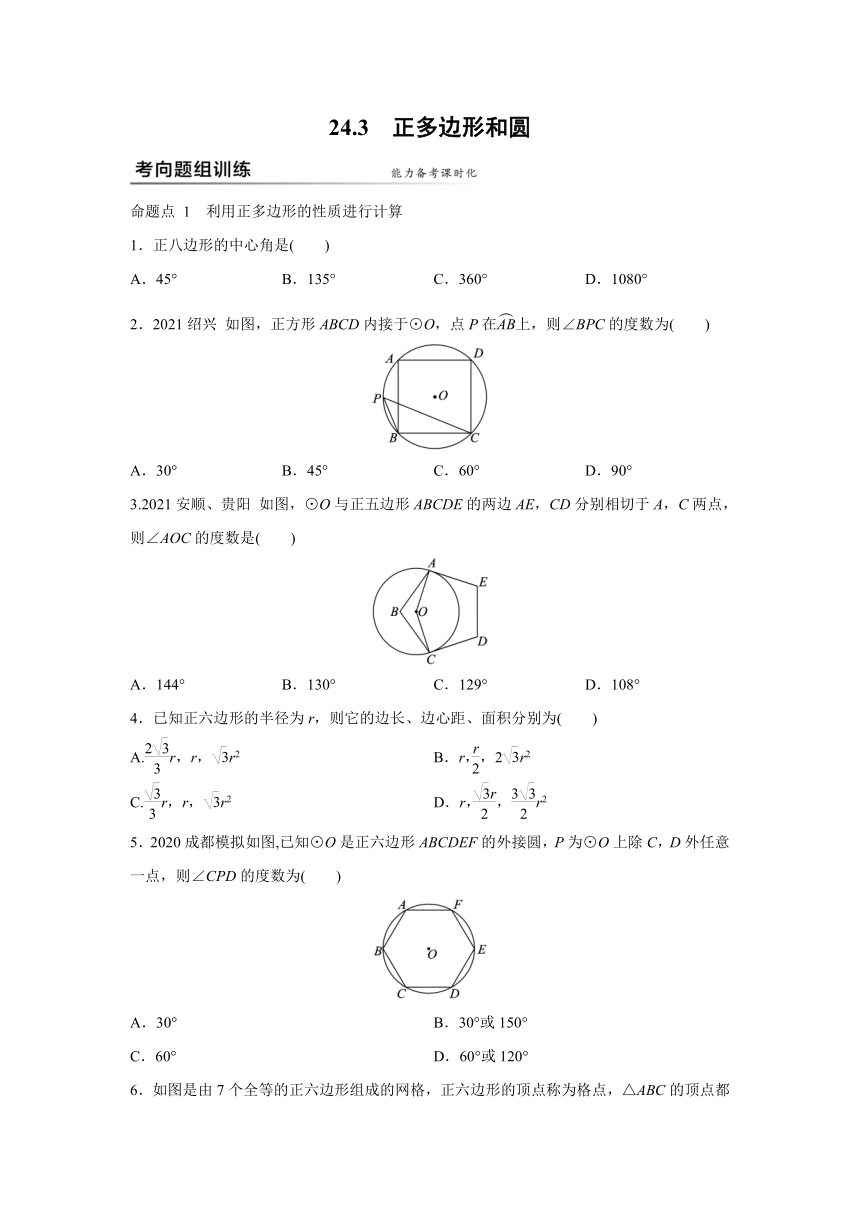
1.正八边形的中心角是( )
A.45° B.135° C.360° D.1080°
2.2021绍兴 如图,正方形ABCD内接于⊙O,点P在上,则∠BPC的度数为( )
A.30° B.45° C.60° D.90°
3.2021安顺、贵阳 如图,⊙O与正五边形ABCDE的两边AE,CD分别相切于A,C两点,则∠AOC的度数是( )
A.144° B.130° C.129° D.108°
4.已知正六边形的半径为r,则它的边长、边心距、面积分别为( )
A.r,r,r2 B.r,,2r2
C.r,r,r2 D.r,,r2
5.2020成都模拟如图,已知⊙O是正六边形ABCDEF的外接圆,P为⊙O上除C,D外任意一点,则∠CPD的度数为( )
A.30° B.30°或150°
C.60° D.60°或120°
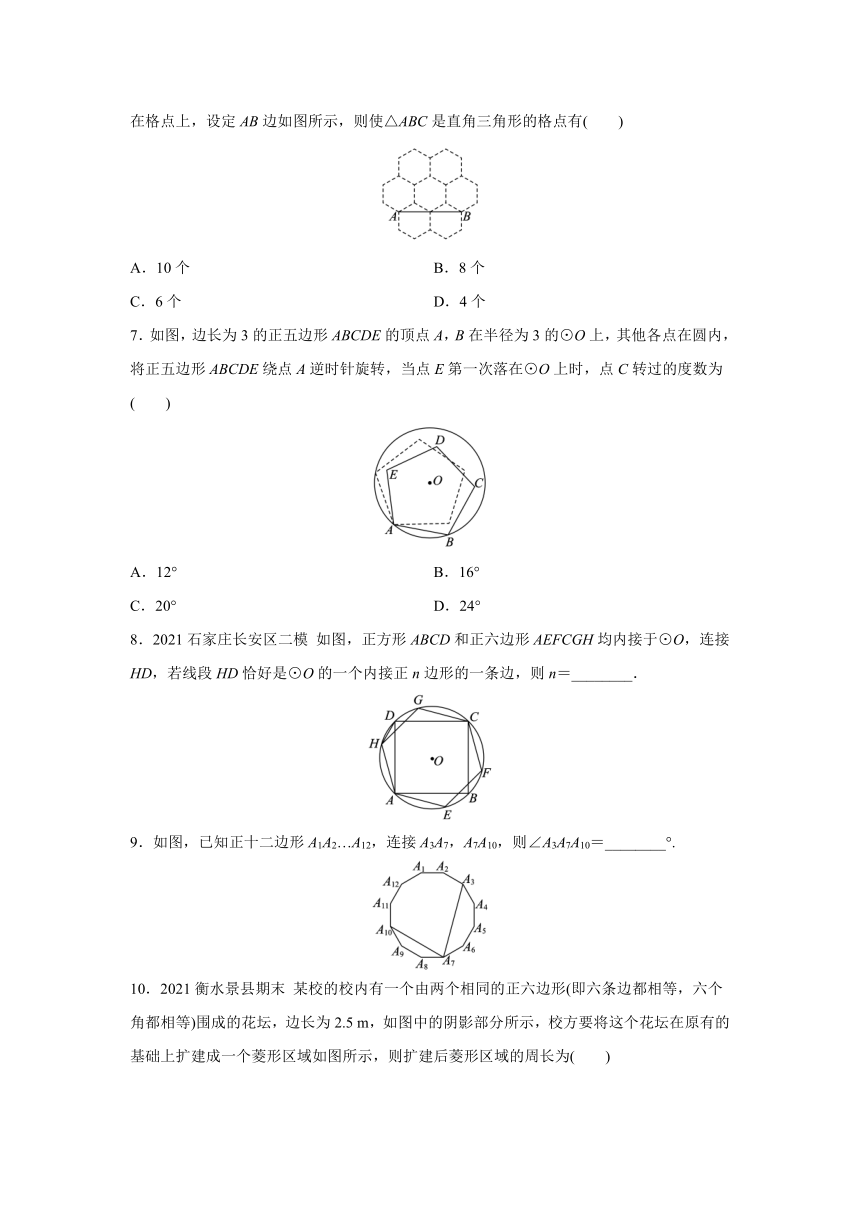
6.如图是由7个全等的正六边形组成的网格,正六边形的顶点称为格点,△ABC的顶点都在格点上,设定AB边如图所示,则使△ABC是直角三角形的格点有( )
A.10个 B.8个
C.6个 D.4个
7.如图,边长为3的正五边形ABCDE的顶点A,B在半径为3的⊙O上,其他各点在圆内,将正五边形ABCDE绕点A逆时针旋转,当点E第一次落在⊙O上时,点C转过的度数为( )
A.12° B.16°
C.20° D.24°
8.2021石家庄长安区二模 如图,正方形ABCD和正六边形AEFCGH均内接于⊙O,连接HD,若线段HD恰好是⊙O的一个内接正n边形的一条边,则n=________.
9.如图,已知正十二边形A1A2…A12,连接A3A7,A7A10,则∠A3A7A10=________°.
10.2021衡水景县期末 某校的校内有一个由两个相同的正六边形(即六条边都相等,六个角都相等)围成的花坛,边长为2.5 m,如图中的阴影部分所示,校方要将这个花坛在原有的基础上扩建成一个菱形区域如图所示,则扩建后菱形区域的周长为( )
A.20 m B.25 m C.30 m D.35 m
11.如图,AB,AC分别为⊙O的内接正方形与内接正三角形的一边,而BC恰好是⊙O内接正n边形的一边,则n等于________.
命题点 2 正多边形的画法
12.下列用尺规等分圆周的作法正确的有( )
①在圆上依次截取等于半径的弦,就可以六等分圆;②作相互垂直的两条直径,就可以四等分圆;③按①的方法将圆六等分,六个等分点中三个不相邻的点三等分圆;④按②的方法将圆四等分,再平分四条弧,就可以八等分圆.
A.4个 B.3个 C.2个 D.1个
13.如图,AD为⊙O的直径,作⊙O的内接正三角形ABC,甲、乙两人的作法分别如图下:
甲:1.以点D为圆心,OD长为半径作圆弧,交⊙O于B,C两点;
2.连接AB,BC,AC.△ABC即为所求作的三角形.
乙:1.作OD的中垂线,交⊙O于B,C两点;
2.连接AB,AC.△ABC即为所求作的三角形.
对于甲、乙两人的作法,可判断( )
A.甲对,乙不对 B.甲不对,乙对
C.两人都对 D.两人都不对
14.如图,M,N分别是⊙O的内接正三角形ABC,正方形ABCD,正五边形ABCDE,…,正n边形ABCDEFG…的边AB,BC上的点,且BM=CN,连接OM,ON.
(1)求图①中∠MON的度数;
(2)图②中∠MON的度数是________,图③中∠MON的度数是___________;
(3)试探究∠MON的度数与正n边形的边数n的关系(直接写出答案).
方法点拨(11题) 在圆中,一条弦若是圆内接正n边形的一边,则只需求出弦所对圆心角的度数,便可求出n.
解题突破(14题) 利用从特殊到一般的数学思想.本题中始终有△OBM≌△OCN,从而有∠MON始终等于正多边形的中心角.
答案
1.A
2.B 连接OB,OC,如图.
∵正方形ABCD内接于⊙O,
∴所对的圆心角为90°,
∴∠BOC=90°,∴∠BPC=∠BOC=45°.
3.A 五边形的内角和为180°×(5-2)=540°,则正五边形每一个内角的度数是108°.
∴∠AED=∠EDC=108°.∵⊙O与正五边形ABCDE的两边AE,CD分别相切于A,C两点,∴∠OAE=∠OCD=90°,∴∠AOC=540°-108°×2-90°×2=144°.
4.D
5.B 连接OC,OD.
∵⊙O是正六边形ABCDEF的外接圆,
∴∠COD=60°.
当点P在上时,∠CPD=∠COD=30°;
当点P在上时,∠CPD=180°-30°=150°.
综上所述,∠CPD的度数为30°或150°.
故选B.
6.A 如图,当AB是直角边时,点C共有6个位置,即有6个直角三角形;当AB是斜边时,点C共有4个位置,即有4个直角三角形.
综上所述,使△ABC是直角三角形的格点有6+4=10(个).故选A.
7.A 设点E第一次落在⊙O上时的对应点为E′,连接OA,OB,OE′,如图.
∵五边形ABCDE为正五边形,
∴∠EAB=108°.
∵正五边形ABCDE绕点A逆时针旋转,点E第一次落在⊙O上的点E′处,
∴AE′=AE=3.
∵OA=AB=OB=OE′=AE′=3,
∴△OAE′,△OAB都为等边三角形,
∴∠OAB=∠OAE′=60°,
∴∠E′AB=120°,
∴∠EAE′=12°,
∴当点E第一次落在⊙O上时,点C转过的度数为12°.
8.12 如图,连接OH,OD,OA.
∵正方形ABCD和正六边形AEFCGH均内接于⊙O,
∴∠HOA==60°,∠DOA==90°,
∴∠DOH=∠DOA-∠HOA=90°-60°=30°,
∴n==12,即HD恰好是⊙O内接正十二边形的一条边.
9.75 设该正十二边形的外心为O,如图,连接A10O和A3O.由题意知,∠A3OA10=×5=150°,
∴∠A3A7A10=75°.
10.C 如图.
∵花坛是由两个相同的正六边形围成的,
∴∠FGM=∠GMN=120°,GM=GF=EF,
∴∠BMG=∠BGM=60°,∴△BMG是等边三角形,∴BG=GM=2.5 m.
同理可证AF=EF=2.5 m,
∴AB=BG+GF+AF=2.5×3=7.5(m),
∴扩建后菱形区域的周长为7.5×4=30(m).故选C.
11.12 连接OA,OB,OC,如图.
∵AB,AC分别为⊙O的内接正方形与内接正三角形的一边,
∴∠AOB=90°,∠AOC=120°,
∴∠BOC=∠AOC-∠AOB=30°,
∴n==12,即BC恰好是⊙O内接正十二边形的一边.
12.A
13.C 由甲的作法可知连接OB,BD,OC,CD后,OB=BD=OD=OC=CD,所以△BOD和△COD都是等边三角形,四边形OBDC是菱形,所以∠BOC=120°,则∠BAC=60°.因为四边形OBDC是菱形,所以AD⊥BC,AD平分BC,所以AB=AC,所以△ABC是等边三角形,所以甲的作法是正确的.由乙的作法可知∠BOC=120°,所以∠BAC=60°.又因为AD⊥BC,所以AD平分BC,所以AB=AC,所以△ABC是等边三角形,所以乙的作法是正确的.故选C.
14.解:(1)方法一:连接OB,OC.
∵正三角形ABC内接于⊙O,
∴∠OBM=∠OCN=30°,∠BOC=120°.
又∵BM=CN,OB=OC,
∴△OBM≌△OCN,∴∠BOM=∠CON,
∴∠MON=∠BOC=120°.
方法二:连接OA,OB.
∵正三角形ABC内接于⊙O,
∴AB=BC,∠OAM=∠OBN=30°,∠AOB=120°.
∵BM=CN,∴AM=BN.
又∵OA=OB,
∴△AOM≌△BON,
∴∠AOM=∠BON,
∴∠MON=∠AOB=120°.
(2)90° 72°
(3)∠MON=°.
命题点 1 利用正多边形的性质进行计算
1.正八边形的中心角是( )
A.45° B.135° C.360° D.1080°
2.2021绍兴 如图,正方形ABCD内接于⊙O,点P在上,则∠BPC的度数为( )
A.30° B.45° C.60° D.90°
3.2021安顺、贵阳 如图,⊙O与正五边形ABCDE的两边AE,CD分别相切于A,C两点,则∠AOC的度数是( )
A.144° B.130° C.129° D.108°
4.已知正六边形的半径为r,则它的边长、边心距、面积分别为( )
A.r,r,r2 B.r,,2r2
C.r,r,r2 D.r,,r2
5.2020成都模拟如图,已知⊙O是正六边形ABCDEF的外接圆,P为⊙O上除C,D外任意一点,则∠CPD的度数为( )
A.30° B.30°或150°
C.60° D.60°或120°
6.如图是由7个全等的正六边形组成的网格,正六边形的顶点称为格点,△ABC的顶点都在格点上,设定AB边如图所示,则使△ABC是直角三角形的格点有( )
A.10个 B.8个
C.6个 D.4个
7.如图,边长为3的正五边形ABCDE的顶点A,B在半径为3的⊙O上,其他各点在圆内,将正五边形ABCDE绕点A逆时针旋转,当点E第一次落在⊙O上时,点C转过的度数为( )
A.12° B.16°
C.20° D.24°
8.2021石家庄长安区二模 如图,正方形ABCD和正六边形AEFCGH均内接于⊙O,连接HD,若线段HD恰好是⊙O的一个内接正n边形的一条边,则n=________.
9.如图,已知正十二边形A1A2…A12,连接A3A7,A7A10,则∠A3A7A10=________°.
10.2021衡水景县期末 某校的校内有一个由两个相同的正六边形(即六条边都相等,六个角都相等)围成的花坛,边长为2.5 m,如图中的阴影部分所示,校方要将这个花坛在原有的基础上扩建成一个菱形区域如图所示,则扩建后菱形区域的周长为( )
A.20 m B.25 m C.30 m D.35 m
11.如图,AB,AC分别为⊙O的内接正方形与内接正三角形的一边,而BC恰好是⊙O内接正n边形的一边,则n等于________.
命题点 2 正多边形的画法
12.下列用尺规等分圆周的作法正确的有( )
①在圆上依次截取等于半径的弦,就可以六等分圆;②作相互垂直的两条直径,就可以四等分圆;③按①的方法将圆六等分,六个等分点中三个不相邻的点三等分圆;④按②的方法将圆四等分,再平分四条弧,就可以八等分圆.
A.4个 B.3个 C.2个 D.1个
13.如图,AD为⊙O的直径,作⊙O的内接正三角形ABC,甲、乙两人的作法分别如图下:
甲:1.以点D为圆心,OD长为半径作圆弧,交⊙O于B,C两点;
2.连接AB,BC,AC.△ABC即为所求作的三角形.
乙:1.作OD的中垂线,交⊙O于B,C两点;
2.连接AB,AC.△ABC即为所求作的三角形.
对于甲、乙两人的作法,可判断( )
A.甲对,乙不对 B.甲不对,乙对
C.两人都对 D.两人都不对
14.如图,M,N分别是⊙O的内接正三角形ABC,正方形ABCD,正五边形ABCDE,…,正n边形ABCDEFG…的边AB,BC上的点,且BM=CN,连接OM,ON.
(1)求图①中∠MON的度数;
(2)图②中∠MON的度数是________,图③中∠MON的度数是___________;
(3)试探究∠MON的度数与正n边形的边数n的关系(直接写出答案).
方法点拨(11题) 在圆中,一条弦若是圆内接正n边形的一边,则只需求出弦所对圆心角的度数,便可求出n.
解题突破(14题) 利用从特殊到一般的数学思想.本题中始终有△OBM≌△OCN,从而有∠MON始终等于正多边形的中心角.
答案
1.A
2.B 连接OB,OC,如图.
∵正方形ABCD内接于⊙O,
∴所对的圆心角为90°,
∴∠BOC=90°,∴∠BPC=∠BOC=45°.
3.A 五边形的内角和为180°×(5-2)=540°,则正五边形每一个内角的度数是108°.
∴∠AED=∠EDC=108°.∵⊙O与正五边形ABCDE的两边AE,CD分别相切于A,C两点,∴∠OAE=∠OCD=90°,∴∠AOC=540°-108°×2-90°×2=144°.
4.D
5.B 连接OC,OD.
∵⊙O是正六边形ABCDEF的外接圆,
∴∠COD=60°.
当点P在上时,∠CPD=∠COD=30°;
当点P在上时,∠CPD=180°-30°=150°.
综上所述,∠CPD的度数为30°或150°.
故选B.
6.A 如图,当AB是直角边时,点C共有6个位置,即有6个直角三角形;当AB是斜边时,点C共有4个位置,即有4个直角三角形.
综上所述,使△ABC是直角三角形的格点有6+4=10(个).故选A.
7.A 设点E第一次落在⊙O上时的对应点为E′,连接OA,OB,OE′,如图.
∵五边形ABCDE为正五边形,
∴∠EAB=108°.
∵正五边形ABCDE绕点A逆时针旋转,点E第一次落在⊙O上的点E′处,
∴AE′=AE=3.
∵OA=AB=OB=OE′=AE′=3,
∴△OAE′,△OAB都为等边三角形,
∴∠OAB=∠OAE′=60°,
∴∠E′AB=120°,
∴∠EAE′=12°,
∴当点E第一次落在⊙O上时,点C转过的度数为12°.
8.12 如图,连接OH,OD,OA.
∵正方形ABCD和正六边形AEFCGH均内接于⊙O,
∴∠HOA==60°,∠DOA==90°,
∴∠DOH=∠DOA-∠HOA=90°-60°=30°,
∴n==12,即HD恰好是⊙O内接正十二边形的一条边.
9.75 设该正十二边形的外心为O,如图,连接A10O和A3O.由题意知,∠A3OA10=×5=150°,
∴∠A3A7A10=75°.
10.C 如图.
∵花坛是由两个相同的正六边形围成的,
∴∠FGM=∠GMN=120°,GM=GF=EF,
∴∠BMG=∠BGM=60°,∴△BMG是等边三角形,∴BG=GM=2.5 m.
同理可证AF=EF=2.5 m,
∴AB=BG+GF+AF=2.5×3=7.5(m),
∴扩建后菱形区域的周长为7.5×4=30(m).故选C.
11.12 连接OA,OB,OC,如图.
∵AB,AC分别为⊙O的内接正方形与内接正三角形的一边,
∴∠AOB=90°,∠AOC=120°,
∴∠BOC=∠AOC-∠AOB=30°,
∴n==12,即BC恰好是⊙O内接正十二边形的一边.
12.A
13.C 由甲的作法可知连接OB,BD,OC,CD后,OB=BD=OD=OC=CD,所以△BOD和△COD都是等边三角形,四边形OBDC是菱形,所以∠BOC=120°,则∠BAC=60°.因为四边形OBDC是菱形,所以AD⊥BC,AD平分BC,所以AB=AC,所以△ABC是等边三角形,所以甲的作法是正确的.由乙的作法可知∠BOC=120°,所以∠BAC=60°.又因为AD⊥BC,所以AD平分BC,所以AB=AC,所以△ABC是等边三角形,所以乙的作法是正确的.故选C.
14.解:(1)方法一:连接OB,OC.
∵正三角形ABC内接于⊙O,
∴∠OBM=∠OCN=30°,∠BOC=120°.
又∵BM=CN,OB=OC,
∴△OBM≌△OCN,∴∠BOM=∠CON,
∴∠MON=∠BOC=120°.
方法二:连接OA,OB.
∵正三角形ABC内接于⊙O,
∴AB=BC,∠OAM=∠OBN=30°,∠AOB=120°.
∵BM=CN,∴AM=BN.
又∵OA=OB,
∴△AOM≌△BON,
∴∠AOM=∠BON,
∴∠MON=∠AOB=120°.
(2)90° 72°
(3)∠MON=°.
同课章节目录
