人教版数学七年级上册同步提优训练:4.1.1第1课时 立体图形与平面图形(word版含答案)
文档属性
| 名称 | 人教版数学七年级上册同步提优训练:4.1.1第1课时 立体图形与平面图形(word版含答案) |
|
|
| 格式 | docx | ||
| 文件大小 | 408.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-07-09 22:25:04 | ||
图片预览

文档简介
第四章 几何图形初步
4.1.1 第1课时 立体图形与平面图形
命题点 1 立体图形的识别与分类
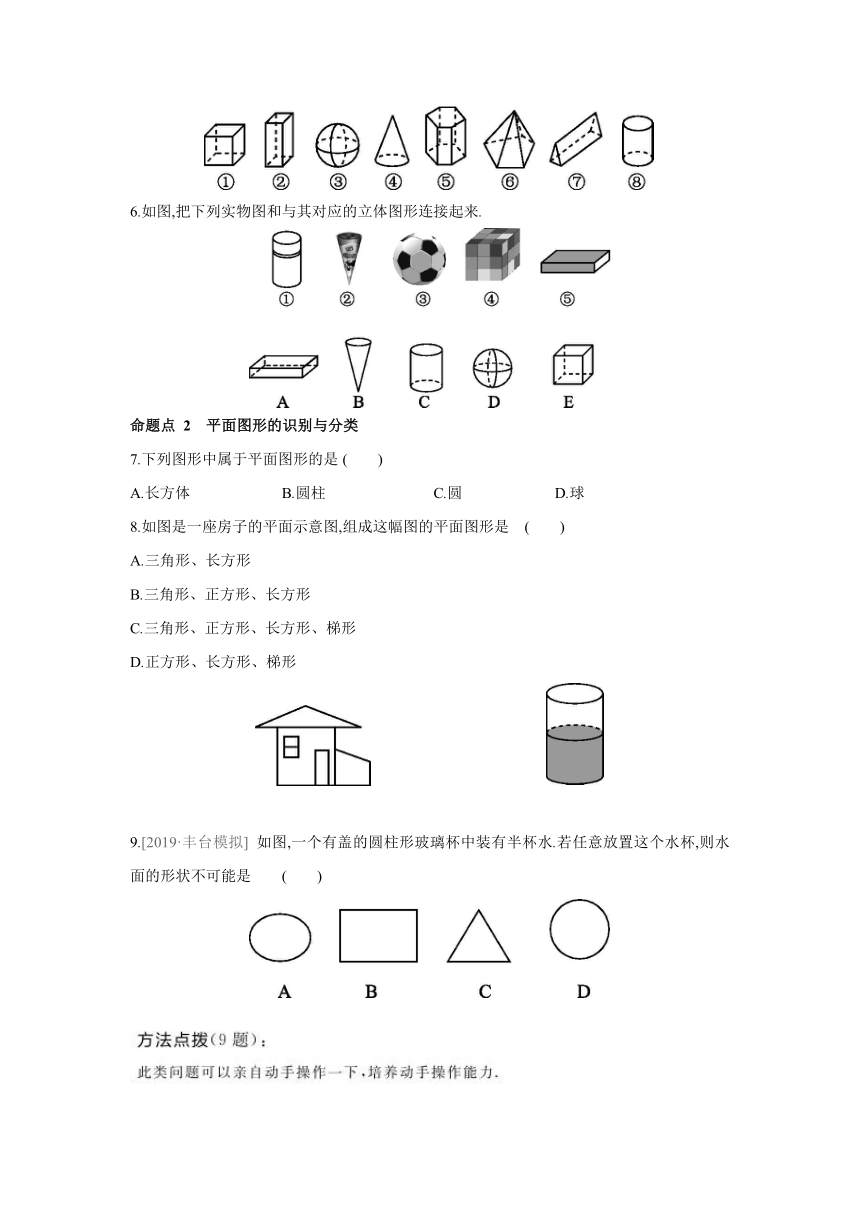
1.下列图形中,属于立体图形的是 ( )
2.如图所示的几何体属于球的是 ( )
3.下面七个几何体中,是棱柱的有 ( )
A.4个 B.3个
C.2个 D.1个
4.把常见的棱柱、棱锥、圆柱、圆锥、球分类,属于柱体的有棱柱、圆柱,属于锥体的有圆锥、棱锥,属于球体的有球.下列几何体中,与其余三个不属于同一类的是 ( )
5.如图所示的8个立体图形中,是柱体的有 ,是锥体的有 ,是球的有 .(填序号)
6.如图,把下列实物图和与其对应的立体图形连接起来.
命题点 2 平面图形的识别与分类
7.下列图形中属于平面图形的是 ( )
A.长方体 B.圆柱 C.圆 D.球
8.如图是一座房子的平面示意图,组成这幅图的平面图形是 ( )
A.三角形、长方形
B.三角形、正方形、长方形
C.三角形、正方形、长方形、梯形
D.正方形、长方形、梯形
9.[2019·丰台模拟] 如图,一个有盖的圆柱形玻璃杯中装有半杯水.若任意放置这个水杯,则水面的形状不可能是 ( )
10.一套七巧板有 种图形,其中有 个平行四边形、 个正方形、 个三角形,用其中的两块大小、形状完全相同的三角形可以拼成 、 、 .
11.如图,下列各几何体的表面中包含哪些平面图形
12.用纸板做两个大小不同的长方体纸盒,尺寸如图(单位:cm).
(1)用含a,b,c的式子表示做这两个纸盒共需用多少纸板;
(2)试计算做大纸盒比做小纸盒多用多少纸板.
13.如图①是三个直立于水平面上的形状完全相同的几何体(下底面为圆,单位:cm),将它们拼成如图②所示的新几何体,求新几何体的体积(结果保留π).
答案
1.C 角、圆、三角形都是平面图形,圆锥是立体图形.
2.B
3.B 如图,①是三棱柱,②是球,③是圆锥,④是三棱锥,⑤是正方体,⑥是圆柱,⑦是六棱柱,因此棱柱有①⑤⑦.故选B.
4.C 正方体、圆柱和四棱柱都是柱体,只有C选项是锥体.故选C.
5.①②⑤⑦⑧ ④⑥ ③
6.①-C,②-B,③-D,④-E,⑤-A 连线略
7.C
8.C
9.C
10.3 1 1 5 三角形 正方形 平行四边形
11.(1)长方形 (2)圆 (3)三角形、平行四边形
12.解:(1)做小长方体纸盒需纸板(2ab+2bc+2ac)cm2;
做大长方体纸盒需纸板2·1.5a·2b+2·2b·2c+2·1.5a·2c=(6ab+8bc+6ac)cm2,
所以做这两个纸盒共需纸板2ab+2bc+2ac+6ab+8bc+6ac=(8ab+10bc+8ac)cm2.
(2)(6ab+8bc+6ac)-(2ab+2bc+2ac)=4ab+6bc+4ac,
所以做大纸盒比做小纸盒多用(4ab+6bc+4ac)cm2的纸板.
13.解:π×22×(4+6)+[π×22×(4+6)]=40π+20π=60π(cm3).
答:新几何体的体积为60π cm3.
4.1.1 第1课时 立体图形与平面图形
命题点 1 立体图形的识别与分类
1.下列图形中,属于立体图形的是 ( )
2.如图所示的几何体属于球的是 ( )
3.下面七个几何体中,是棱柱的有 ( )
A.4个 B.3个
C.2个 D.1个
4.把常见的棱柱、棱锥、圆柱、圆锥、球分类,属于柱体的有棱柱、圆柱,属于锥体的有圆锥、棱锥,属于球体的有球.下列几何体中,与其余三个不属于同一类的是 ( )
5.如图所示的8个立体图形中,是柱体的有 ,是锥体的有 ,是球的有 .(填序号)
6.如图,把下列实物图和与其对应的立体图形连接起来.
命题点 2 平面图形的识别与分类
7.下列图形中属于平面图形的是 ( )
A.长方体 B.圆柱 C.圆 D.球
8.如图是一座房子的平面示意图,组成这幅图的平面图形是 ( )
A.三角形、长方形
B.三角形、正方形、长方形
C.三角形、正方形、长方形、梯形
D.正方形、长方形、梯形
9.[2019·丰台模拟] 如图,一个有盖的圆柱形玻璃杯中装有半杯水.若任意放置这个水杯,则水面的形状不可能是 ( )
10.一套七巧板有 种图形,其中有 个平行四边形、 个正方形、 个三角形,用其中的两块大小、形状完全相同的三角形可以拼成 、 、 .
11.如图,下列各几何体的表面中包含哪些平面图形
12.用纸板做两个大小不同的长方体纸盒,尺寸如图(单位:cm).
(1)用含a,b,c的式子表示做这两个纸盒共需用多少纸板;
(2)试计算做大纸盒比做小纸盒多用多少纸板.
13.如图①是三个直立于水平面上的形状完全相同的几何体(下底面为圆,单位:cm),将它们拼成如图②所示的新几何体,求新几何体的体积(结果保留π).
答案
1.C 角、圆、三角形都是平面图形,圆锥是立体图形.
2.B
3.B 如图,①是三棱柱,②是球,③是圆锥,④是三棱锥,⑤是正方体,⑥是圆柱,⑦是六棱柱,因此棱柱有①⑤⑦.故选B.
4.C 正方体、圆柱和四棱柱都是柱体,只有C选项是锥体.故选C.
5.①②⑤⑦⑧ ④⑥ ③
6.①-C,②-B,③-D,④-E,⑤-A 连线略
7.C
8.C
9.C
10.3 1 1 5 三角形 正方形 平行四边形
11.(1)长方形 (2)圆 (3)三角形、平行四边形
12.解:(1)做小长方体纸盒需纸板(2ab+2bc+2ac)cm2;
做大长方体纸盒需纸板2·1.5a·2b+2·2b·2c+2·1.5a·2c=(6ab+8bc+6ac)cm2,
所以做这两个纸盒共需纸板2ab+2bc+2ac+6ab+8bc+6ac=(8ab+10bc+8ac)cm2.
(2)(6ab+8bc+6ac)-(2ab+2bc+2ac)=4ab+6bc+4ac,
所以做大纸盒比做小纸盒多用(4ab+6bc+4ac)cm2的纸板.
13.解:π×22×(4+6)+[π×22×(4+6)]=40π+20π=60π(cm3).
答:新几何体的体积为60π cm3.
