人教版数学七年级上册同步提优训练:4.2第1课时 直线、射线、线段的概念(word版含答案)
文档属性
| 名称 | 人教版数学七年级上册同步提优训练:4.2第1课时 直线、射线、线段的概念(word版含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 223.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-07-09 22:38:41 | ||
图片预览


文档简介
4.2 第1课时 直线、射线、线段的概念
命题点 1 经过两点有且只有一条直线
1.木匠在木料上画线,先确定两个点的位置,就能把线画得很准确,其依据是 ( )
A.两点确定一条直线 B.两点确定一条线段
C.过一点有一条直线 D.过一点有无数条直线
2.经过同一平面内A,B,C三点可连接直线的条数为 ( )
A.1条 B.3条
C.3条或1条 D.不能确定
3.如图,建筑工人在砌墙时,经常用细线绳在墙的两端之间拉一条参照线,使垒的每一层砖在一条直线上.这样做的依据是 .
平面上有四个点,经过其中每两个点画一条直线,那么一共可以画直线 条.
5.小明和小亮在讨论“射击时为什么枪管上要有准星 ”这一问题.
小明说:“经过两点有一条直线,并且只有一条直线,所以枪管上要有准星.”
小亮说:“若将人眼看成一点,准星看成一点,目标看成一点,这不就有三点了吗 不是三点确定一条直线吗 ”
你认为他们两个谁的说法正确
命题点 2 直线、线段、射线的区别与表示
6.下列说法正确的是 ( )
A.直线AB和直线BA是两条直线
B.射线AB和射线BA是两条射线
C.线段AB和线段BA是两条线段
D.直线AB和直线a不可能是同一条直线
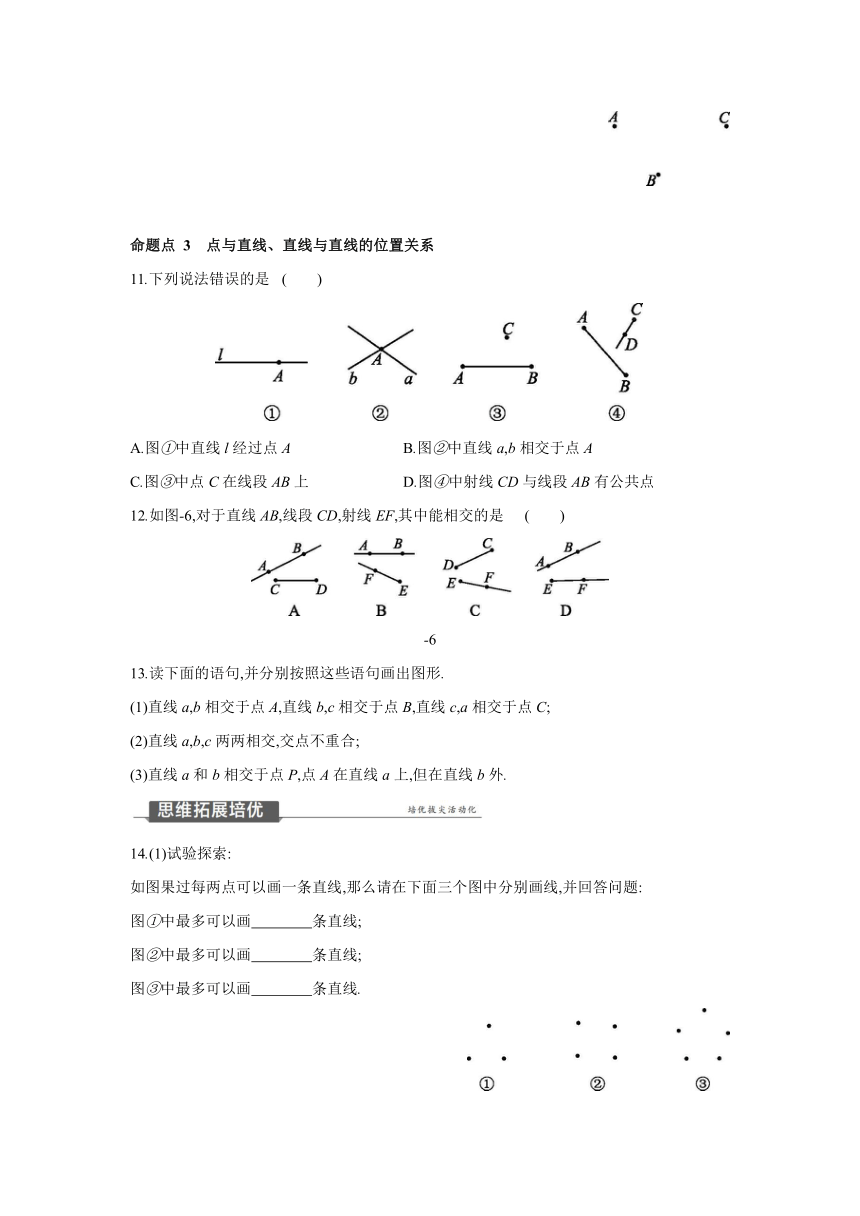
7.如图所示,下列对图形描述不正确的是 ( )
A.直线AB B.直线BC
C.射线AC D.射线AB
8.下列说法正确的是 ( )
A.画一条长3 cm的射线 B.射线、线段、直线中,直线最长
C.射线是直线的一部分 D.延长直线AB到点C
9.如图所示,若图中共有m条线段,n条射线,则m+n= .
如图,已知三点A,B,C.
(1)画出直线AC,线段BC,射线AB;
(2)在线段BC上任取一点D(不同于点B,C),画线段AD;
(3)数数看,此时图中共有 条线段.
命题点 3 点与直线、直线与直线的位置关系
11.下列说法错误的是 ( )
A.图①中直线l经过点A B.图②中直线a,b相交于点A
C.图③中点C在线段AB上 D.图④中射线CD与线段AB有公共点
12.如图-6,对于直线AB,线段CD,射线EF,其中能相交的是 ( )
-6
13.读下面的语句,并分别按照这些语句画出图形.
(1)直线a,b相交于点A,直线b,c相交于点B,直线c,a相交于点C;
(2)直线a,b,c两两相交,交点不重合;
(3)直线a和b相交于点P,点A在直线a上,但在直线b外.
14.(1)试验探索:
如图果过每两点可以画一条直线,那么请在下面三个图中分别画线,并回答问题:
图①中最多可以画 条直线;
图②中最多可以画 条直线;
图③中最多可以画 条直线.
(2)归纳结论:
如图果平面上有n(n≥3)个点,且每三个点均不在一条直线上,那么最多可以画出直线 条.(用含n的式子表示)
(3)解决问题:
某班50名同学在毕业后的一次聚会中,若每两人握一次手问好,则共握 次手;最后,每两个人要互赠礼物留念,则共需 件礼物.
15.(1)观察思考:
如图,线段AB上有C,D两点,计算图中共有多少条线段;
(2)模型构建:
如图果线段上有m个点(包括线段的两个端点),那么这条线段上以这m个点为端点的线段共有多少条 说明理由;
(3)拓展应用:
8名同学参加班级组织的象棋比赛,比赛采用单循环制(即每两名同学之间都要进行一场比赛),那么一共要进行多少场比赛
典题讲评与答案详析
1.A 2.C
3.两点确定一条直线
4.1或4或6 [解析] ①当四点共线时,经过每两个点画一条直线,那么共可以画1条直线;②当只有三点共线时,经过每两个点画一条直线,那么共可以画4条直线;③当每三点不共线时,经过每两个点画一条直线,那么共可以画6条直线.故答案为:1或4或6.
5.解:小明的说法正确,小亮的说法不正确.
如图果将人眼看成一点,准星看成一点,目标看成一点,那么要想射中目标,目标必须在人眼与准星确定的直线上,换句话说要想射中目标就必须使准星在人眼与目标所确定的直线上.
6.B 7.B
8.C [解析] A.画一条长3 cm的射线,说法错误,射线可以向一个方向无限延伸;
B.射线、线段、直线中,直线最长,说法错误,射线可以向一个方向无限延伸,直线可以向两个方向无限延伸;
C.射线是直线的一部分,正确;
D.延长直线AB到点C,说法错误,直线可以向两个方向无限延伸.
故选C.
9.26 [解析] 图中有线段OA,OB,OC,OD,AC,BD,AB,BC,CD,AD,共10条,射线共16条,
所以m=10,n=16.
所以m+n=26.
故答案为:26.
10.解:(1)(2)如图所示:
(3)6
11.C 12.B
13.解:(1)如图所示.
(2)如图所示.
(3)如图所示.
14.解:(1)如图:
3 6 10
(2) (3)1225 2450
15.解:(1)因为以点A为左端点的线段有线段AB,AC,AD,
以点C为左端点的线段有线段CD,CB,
以点D为左端点的线段有线段DB,
所以共有3+2+1=6(条)线段.
(2)有条.
理由:线段上有m个点(包括线段的两个端点),每一个点都可以与其他点构成(m-1)条线段,一共能构成m(m-1)条,但由于线段端点的无序性,所有线段都被重复计算了一次,所以该条线段上以这m个点为端点的线段共有条.
(3)把8名同学看作直线上的8个点,每两名同学之间的一场比赛看作一条线段,
直线上以这8个点为端点所构成的线段条数就等于比赛的场数,因此一共要进行=28(场)比赛.
命题点 1 经过两点有且只有一条直线
1.木匠在木料上画线,先确定两个点的位置,就能把线画得很准确,其依据是 ( )
A.两点确定一条直线 B.两点确定一条线段
C.过一点有一条直线 D.过一点有无数条直线
2.经过同一平面内A,B,C三点可连接直线的条数为 ( )
A.1条 B.3条
C.3条或1条 D.不能确定
3.如图,建筑工人在砌墙时,经常用细线绳在墙的两端之间拉一条参照线,使垒的每一层砖在一条直线上.这样做的依据是 .
平面上有四个点,经过其中每两个点画一条直线,那么一共可以画直线 条.
5.小明和小亮在讨论“射击时为什么枪管上要有准星 ”这一问题.
小明说:“经过两点有一条直线,并且只有一条直线,所以枪管上要有准星.”
小亮说:“若将人眼看成一点,准星看成一点,目标看成一点,这不就有三点了吗 不是三点确定一条直线吗 ”
你认为他们两个谁的说法正确
命题点 2 直线、线段、射线的区别与表示
6.下列说法正确的是 ( )
A.直线AB和直线BA是两条直线
B.射线AB和射线BA是两条射线
C.线段AB和线段BA是两条线段
D.直线AB和直线a不可能是同一条直线
7.如图所示,下列对图形描述不正确的是 ( )
A.直线AB B.直线BC
C.射线AC D.射线AB
8.下列说法正确的是 ( )
A.画一条长3 cm的射线 B.射线、线段、直线中,直线最长
C.射线是直线的一部分 D.延长直线AB到点C
9.如图所示,若图中共有m条线段,n条射线,则m+n= .
如图,已知三点A,B,C.
(1)画出直线AC,线段BC,射线AB;
(2)在线段BC上任取一点D(不同于点B,C),画线段AD;
(3)数数看,此时图中共有 条线段.
命题点 3 点与直线、直线与直线的位置关系
11.下列说法错误的是 ( )
A.图①中直线l经过点A B.图②中直线a,b相交于点A
C.图③中点C在线段AB上 D.图④中射线CD与线段AB有公共点
12.如图-6,对于直线AB,线段CD,射线EF,其中能相交的是 ( )
-6
13.读下面的语句,并分别按照这些语句画出图形.
(1)直线a,b相交于点A,直线b,c相交于点B,直线c,a相交于点C;
(2)直线a,b,c两两相交,交点不重合;
(3)直线a和b相交于点P,点A在直线a上,但在直线b外.
14.(1)试验探索:
如图果过每两点可以画一条直线,那么请在下面三个图中分别画线,并回答问题:
图①中最多可以画 条直线;
图②中最多可以画 条直线;
图③中最多可以画 条直线.
(2)归纳结论:
如图果平面上有n(n≥3)个点,且每三个点均不在一条直线上,那么最多可以画出直线 条.(用含n的式子表示)
(3)解决问题:
某班50名同学在毕业后的一次聚会中,若每两人握一次手问好,则共握 次手;最后,每两个人要互赠礼物留念,则共需 件礼物.
15.(1)观察思考:
如图,线段AB上有C,D两点,计算图中共有多少条线段;
(2)模型构建:
如图果线段上有m个点(包括线段的两个端点),那么这条线段上以这m个点为端点的线段共有多少条 说明理由;
(3)拓展应用:
8名同学参加班级组织的象棋比赛,比赛采用单循环制(即每两名同学之间都要进行一场比赛),那么一共要进行多少场比赛
典题讲评与答案详析
1.A 2.C
3.两点确定一条直线
4.1或4或6 [解析] ①当四点共线时,经过每两个点画一条直线,那么共可以画1条直线;②当只有三点共线时,经过每两个点画一条直线,那么共可以画4条直线;③当每三点不共线时,经过每两个点画一条直线,那么共可以画6条直线.故答案为:1或4或6.
5.解:小明的说法正确,小亮的说法不正确.
如图果将人眼看成一点,准星看成一点,目标看成一点,那么要想射中目标,目标必须在人眼与准星确定的直线上,换句话说要想射中目标就必须使准星在人眼与目标所确定的直线上.
6.B 7.B
8.C [解析] A.画一条长3 cm的射线,说法错误,射线可以向一个方向无限延伸;
B.射线、线段、直线中,直线最长,说法错误,射线可以向一个方向无限延伸,直线可以向两个方向无限延伸;
C.射线是直线的一部分,正确;
D.延长直线AB到点C,说法错误,直线可以向两个方向无限延伸.
故选C.
9.26 [解析] 图中有线段OA,OB,OC,OD,AC,BD,AB,BC,CD,AD,共10条,射线共16条,
所以m=10,n=16.
所以m+n=26.
故答案为:26.
10.解:(1)(2)如图所示:
(3)6
11.C 12.B
13.解:(1)如图所示.
(2)如图所示.
(3)如图所示.
14.解:(1)如图:
3 6 10
(2) (3)1225 2450
15.解:(1)因为以点A为左端点的线段有线段AB,AC,AD,
以点C为左端点的线段有线段CD,CB,
以点D为左端点的线段有线段DB,
所以共有3+2+1=6(条)线段.
(2)有条.
理由:线段上有m个点(包括线段的两个端点),每一个点都可以与其他点构成(m-1)条线段,一共能构成m(m-1)条,但由于线段端点的无序性,所有线段都被重复计算了一次,所以该条线段上以这m个点为端点的线段共有条.
(3)把8名同学看作直线上的8个点,每两名同学之间的一场比赛看作一条线段,
直线上以这8个点为端点所构成的线段条数就等于比赛的场数,因此一共要进行=28(场)比赛.
