人教版数学八年级上册同步提优训练:11.3.2 多边形的内角和(word版含答案)
文档属性
| 名称 | 人教版数学八年级上册同步提优训练:11.3.2 多边形的内角和(word版含答案) |

|
|
| 格式 | docx | ||
| 文件大小 | 250.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-07-09 23:11:44 | ||
图片预览

文档简介
11.3.2 多边形的内角和
命题点 1 多边形内角和公式的探究
1.如图,某学生探究n边形的内角和公式,首先将点A1与A3,A4,A5,…,An-1连接,将此n边形分割成(n-2)个三角形,然后由每个三角形的内角和为180°,可得n边形的内角和为(n-2)×180°.该同学的上述探究方法所体现的数学思想是 ( )
A.分类讨论思想 B.公理化思想
C.类比思想 D.转化思想
2.佳佳和音音分别设计了一种求n边形的内角和的方案:
(1)佳佳是在n边形内取一点P,然后分别连接PA1,PA2,…,PAn(如图①);
(2)音音是在n边形的一边A1A2上任取一点P(不与点A1,A2重合),然后分别连接PA3,PA4,…,PAn(如图图②).
请你判断这两种方案是否可行,如图果不可行,请你说明理由;如图果可行,请你按方案的设计思路求出多边形的内角和.
命题点 2 与多边形内角和公式有关的计算
3.[2020·淮安] 六边形的内角和为 ( )
A.360° B.540° C.720° D.1080°
4.[2020·济宁] 一个多边形的内角和是1080°,则这个多边形的边数是 ( )
A.9 B.8 C.7 D.6
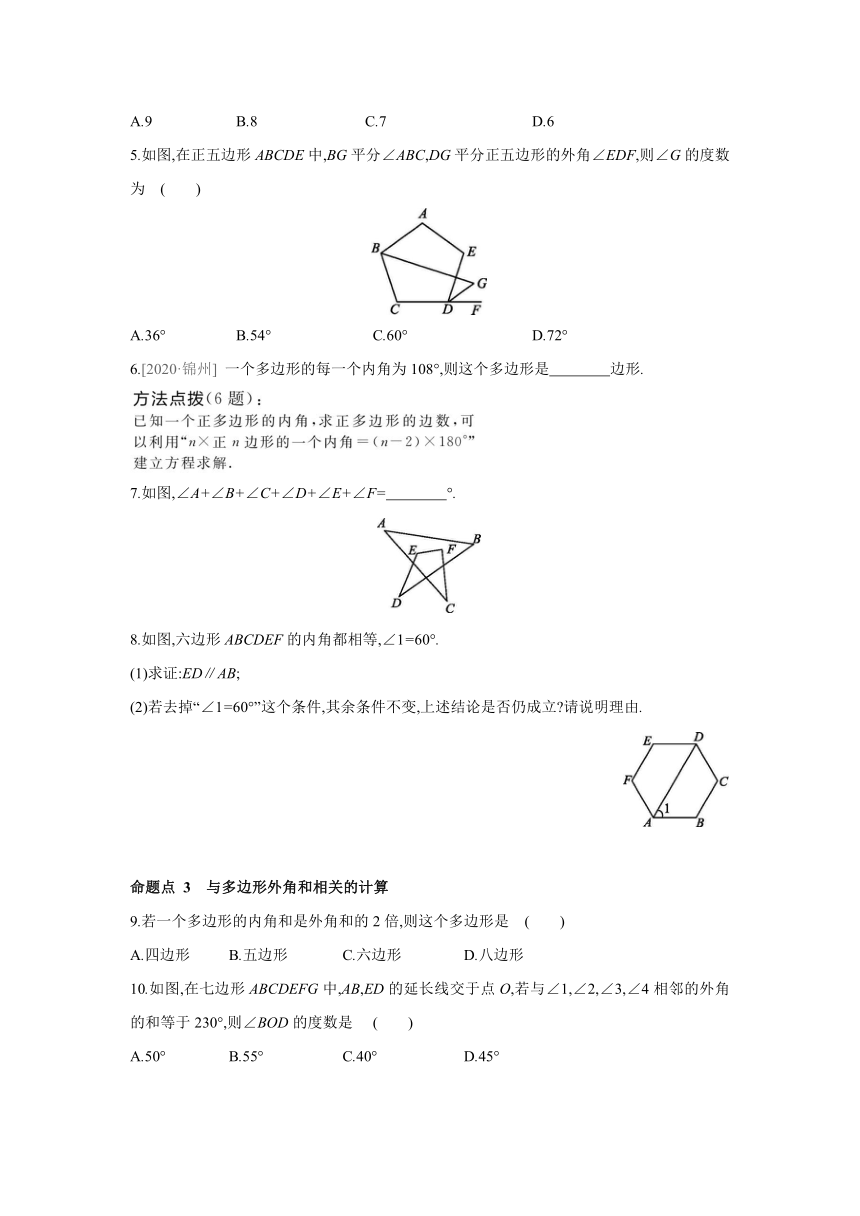
5.如图,在正五边形ABCDE中,BG平分∠ABC,DG平分正五边形的外角∠EDF,则∠G的度数为 ( )
A.36° B.54° C.60° D.72°
6.[2020·锦州] 一个多边形的每一个内角为108°,则这个多边形是 边形.
7.如图,∠A+∠B+∠C+∠D+∠E+∠F= °.
8.如图,六边形ABCDEF的内角都相等,∠1=60°.
(1)求证:ED∥AB;
(2)若去掉“∠1=60°”这个条件,其余条件不变,上述结论是否仍成立 请说明理由.
命题点 3 与多边形外角和相关的计算
9.若一个多边形的内角和是外角和的2倍,则这个多边形是 ( )
A.四边形 B.五边形 C.六边形 D.八边形
10.如图,在七边形ABCDEFG中,AB,ED的延长线交于点O,若与∠1,∠2,∠3,∠4相邻的外角的和等于230°,则∠BOD的度数是 ( )
A.50° B.55° C.40° D.45°
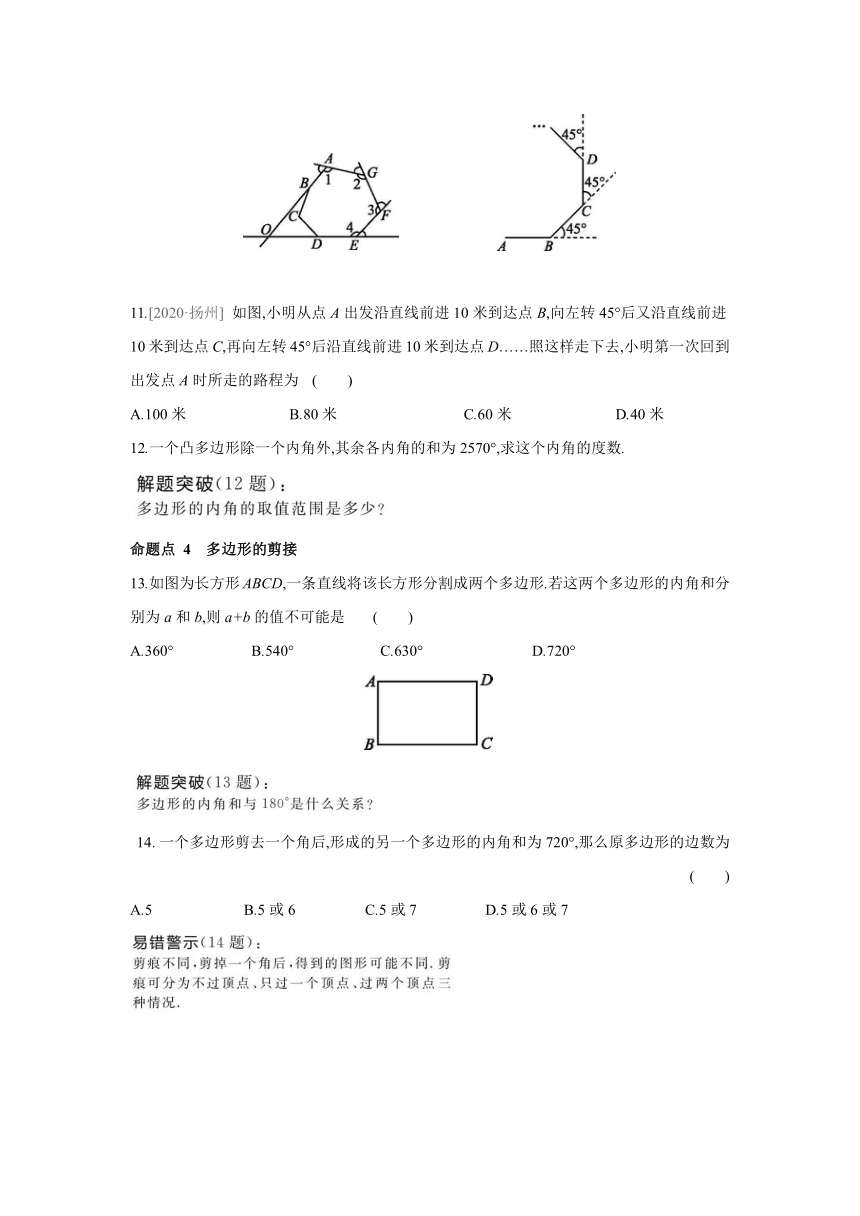
11.[2020·扬州] 如图,小明从点A出发沿直线前进10米到达点B,向左转45°后又沿直线前进10米到达点C,再向左转45°后沿直线前进10米到达点D……照这样走下去,小明第一次回到出发点A时所走的路程为 ( )
A.100米 B.80米 C.60米 D.40米
12.一个凸多边形除一个内角外,其余各内角的和为2570°,求这个内角的度数.
命题点 4 多边形的剪接
13.如图为长方形ABCD,一条直线将该长方形分割成两个多边形.若这两个多边形的内角和分别为a和b,则a+b的值不可能是 ( )
A.360° B.540° C.630° D.720°
一个多边形剪去一个角后,形成的另一个多边形的内角和为720°,那么原多边形的边数为 ( )
A.5 B.5或6 C.5或7 D.5或6或7
15.把一个多边形沿着几条直线剪开,分割成若干个多边形.分割后的多边形的边数总和比原多边形的边数多13条,内角和是原多边形内角和的1.3倍.原来的多边形是几边形 把原来的多边形分割成了多少个多边形
答案
1.D
2.解:这两种方案都是可行的.
佳佳的方案:由题意得n边形被分为n个三角形,则多边形的内角和=n×180°-360°=(n-2)×180°;
音音的方案:由题意得n边形被分为(n-1)个三角形,则多边形的内角和=(n-1)×180°-180°=(n-2)×180°.
3.C 4.B
5.B
6.五 设多边形的边数是n,则108n=(n-2)×180,解得n=5.
故答案为五.
7.360 如图图,连接CD.
∵在△CDM和△ABM中,∠DMC=∠BMA,
∴∠A+∠B=∠BDC+∠ACD.
∴∠A+∠B+∠ACF+∠BDE+∠E+∠F=∠BDC+∠ACD+∠ACF+∠BDE+∠E+∠F=∠EDC+∠FCD+∠E+∠F=360°.
故答案为360.
8.解:(1)证明:六边形的内角和为(6-2)×180°=720°.
∵六边形ABCDEF的内角都相等,
∴每个内角的度数为720°÷6=120°.
又∵∠1=60°,四边形ABCD的内角和为360°,
∴∠CDA=360°-∠1-∠B-∠C=360°-60°-120°-120°=60°.
∴∠EDA=120°-∠CDA=120°-60°=60°.
∴∠EDA=∠1.∴ED∥AB.
(2)成立.理由如图下:如图图,∵六边形ABCDEF的内角和为(6-2)×180°=720°,六边形ABCDEF的内角都相等,∴每个内角的度数为720°÷6=120°.
又∵四边形ABCD的内角和为360°,
∴∠CDA+∠1=360°-120°-120°=120°.
∵∠2+∠CDA=120°,∴∠1=∠2.∴ED∥AB.
9.C 设所求多边形的边数为n.
由题意得(n-2)×180°=360°×2,解得n=6.
则这个多边形是六边形.
10.A ∵五边形AOEFG的外角和是360°,与∠1,∠2,∠3,∠4相邻的外角的和为230°,
∴与∠BOD相邻的外角是360°-230°=130°.
∴∠BOD=180°-130°=50°.
故选A.
11.B ∵小明每次都是沿直线前进10米后向左转45度,
∴他走过的图形是正多边形,正多边形的边数n=360°÷45°=8.
∴他第一次回到出发点A时,一共走了8×10=80(米).
故选B.
12.解:设这个多边形是n边形,这个内角的度数为x.
由题意,得(n-2)×180°=2570°+x,
∴x=(n-2)×180°-2570°,
化简得x=180°n-2930°.
∵0°解得16又∵n为正整数,∴n=17,
∴这个多边形的内角和为(17-2)×180°=2700°,
即这个内角的度数是2700°-2570°=130°.
13.C 一条直线将该长方形ABCD分割成两个多边形,每一个多边形的内角和都是180°的整数倍.分析四个答案,只有630°不能被180°整除,所以a+b的值不可能是630°.
故选C.
14.D
15.解:设原多边形的边数是n,分割成边数分别为a1,a2,…,am的m个多边形,则这m个多边形的总边数为a1+a2+…+am.
由题意得a1+a2+…+am=n+13,
180(a1-2)+180(a2-2)+…+180(am-2)=1.3×180(n-2),则3n+20m=156.
∵m,n均为正整数,∴m=3,n=32(不合题意,舍去)或m=6,n=12.
故原来的多边形是十二边形,把原来的多边形分割成了6个多边形..
命题点 1 多边形内角和公式的探究
1.如图,某学生探究n边形的内角和公式,首先将点A1与A3,A4,A5,…,An-1连接,将此n边形分割成(n-2)个三角形,然后由每个三角形的内角和为180°,可得n边形的内角和为(n-2)×180°.该同学的上述探究方法所体现的数学思想是 ( )
A.分类讨论思想 B.公理化思想
C.类比思想 D.转化思想
2.佳佳和音音分别设计了一种求n边形的内角和的方案:
(1)佳佳是在n边形内取一点P,然后分别连接PA1,PA2,…,PAn(如图①);
(2)音音是在n边形的一边A1A2上任取一点P(不与点A1,A2重合),然后分别连接PA3,PA4,…,PAn(如图图②).
请你判断这两种方案是否可行,如图果不可行,请你说明理由;如图果可行,请你按方案的设计思路求出多边形的内角和.
命题点 2 与多边形内角和公式有关的计算
3.[2020·淮安] 六边形的内角和为 ( )
A.360° B.540° C.720° D.1080°
4.[2020·济宁] 一个多边形的内角和是1080°,则这个多边形的边数是 ( )
A.9 B.8 C.7 D.6
5.如图,在正五边形ABCDE中,BG平分∠ABC,DG平分正五边形的外角∠EDF,则∠G的度数为 ( )
A.36° B.54° C.60° D.72°
6.[2020·锦州] 一个多边形的每一个内角为108°,则这个多边形是 边形.
7.如图,∠A+∠B+∠C+∠D+∠E+∠F= °.
8.如图,六边形ABCDEF的内角都相等,∠1=60°.
(1)求证:ED∥AB;
(2)若去掉“∠1=60°”这个条件,其余条件不变,上述结论是否仍成立 请说明理由.
命题点 3 与多边形外角和相关的计算
9.若一个多边形的内角和是外角和的2倍,则这个多边形是 ( )
A.四边形 B.五边形 C.六边形 D.八边形
10.如图,在七边形ABCDEFG中,AB,ED的延长线交于点O,若与∠1,∠2,∠3,∠4相邻的外角的和等于230°,则∠BOD的度数是 ( )
A.50° B.55° C.40° D.45°
11.[2020·扬州] 如图,小明从点A出发沿直线前进10米到达点B,向左转45°后又沿直线前进10米到达点C,再向左转45°后沿直线前进10米到达点D……照这样走下去,小明第一次回到出发点A时所走的路程为 ( )
A.100米 B.80米 C.60米 D.40米
12.一个凸多边形除一个内角外,其余各内角的和为2570°,求这个内角的度数.
命题点 4 多边形的剪接
13.如图为长方形ABCD,一条直线将该长方形分割成两个多边形.若这两个多边形的内角和分别为a和b,则a+b的值不可能是 ( )
A.360° B.540° C.630° D.720°
一个多边形剪去一个角后,形成的另一个多边形的内角和为720°,那么原多边形的边数为 ( )
A.5 B.5或6 C.5或7 D.5或6或7
15.把一个多边形沿着几条直线剪开,分割成若干个多边形.分割后的多边形的边数总和比原多边形的边数多13条,内角和是原多边形内角和的1.3倍.原来的多边形是几边形 把原来的多边形分割成了多少个多边形
答案
1.D
2.解:这两种方案都是可行的.
佳佳的方案:由题意得n边形被分为n个三角形,则多边形的内角和=n×180°-360°=(n-2)×180°;
音音的方案:由题意得n边形被分为(n-1)个三角形,则多边形的内角和=(n-1)×180°-180°=(n-2)×180°.
3.C 4.B
5.B
6.五 设多边形的边数是n,则108n=(n-2)×180,解得n=5.
故答案为五.
7.360 如图图,连接CD.
∵在△CDM和△ABM中,∠DMC=∠BMA,
∴∠A+∠B=∠BDC+∠ACD.
∴∠A+∠B+∠ACF+∠BDE+∠E+∠F=∠BDC+∠ACD+∠ACF+∠BDE+∠E+∠F=∠EDC+∠FCD+∠E+∠F=360°.
故答案为360.
8.解:(1)证明:六边形的内角和为(6-2)×180°=720°.
∵六边形ABCDEF的内角都相等,
∴每个内角的度数为720°÷6=120°.
又∵∠1=60°,四边形ABCD的内角和为360°,
∴∠CDA=360°-∠1-∠B-∠C=360°-60°-120°-120°=60°.
∴∠EDA=120°-∠CDA=120°-60°=60°.
∴∠EDA=∠1.∴ED∥AB.
(2)成立.理由如图下:如图图,∵六边形ABCDEF的内角和为(6-2)×180°=720°,六边形ABCDEF的内角都相等,∴每个内角的度数为720°÷6=120°.
又∵四边形ABCD的内角和为360°,
∴∠CDA+∠1=360°-120°-120°=120°.
∵∠2+∠CDA=120°,∴∠1=∠2.∴ED∥AB.
9.C 设所求多边形的边数为n.
由题意得(n-2)×180°=360°×2,解得n=6.
则这个多边形是六边形.
10.A ∵五边形AOEFG的外角和是360°,与∠1,∠2,∠3,∠4相邻的外角的和为230°,
∴与∠BOD相邻的外角是360°-230°=130°.
∴∠BOD=180°-130°=50°.
故选A.
11.B ∵小明每次都是沿直线前进10米后向左转45度,
∴他走过的图形是正多边形,正多边形的边数n=360°÷45°=8.
∴他第一次回到出发点A时,一共走了8×10=80(米).
故选B.
12.解:设这个多边形是n边形,这个内角的度数为x.
由题意,得(n-2)×180°=2570°+x,
∴x=(n-2)×180°-2570°,
化简得x=180°n-2930°.
∵0°
∴这个多边形的内角和为(17-2)×180°=2700°,
即这个内角的度数是2700°-2570°=130°.
13.C 一条直线将该长方形ABCD分割成两个多边形,每一个多边形的内角和都是180°的整数倍.分析四个答案,只有630°不能被180°整除,所以a+b的值不可能是630°.
故选C.
14.D
15.解:设原多边形的边数是n,分割成边数分别为a1,a2,…,am的m个多边形,则这m个多边形的总边数为a1+a2+…+am.
由题意得a1+a2+…+am=n+13,
180(a1-2)+180(a2-2)+…+180(am-2)=1.3×180(n-2),则3n+20m=156.
∵m,n均为正整数,∴m=3,n=32(不合题意,舍去)或m=6,n=12.
故原来的多边形是十二边形,把原来的多边形分割成了6个多边形..
