人教版数学八年级上册同步提优训练:13.2 用坐标表示轴对称(第2课时)(Word版含答案)
文档属性
| 名称 | 人教版数学八年级上册同步提优训练:13.2 用坐标表示轴对称(第2课时)(Word版含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 285.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-07-10 10:30:09 | ||
图片预览


文档简介
13.2 第2课时 用坐标表示轴对称
命题点 1 关于坐标轴对称的点的坐标
1.在平面直角坐标系中,点P(-2,5)关于y轴对称的点的坐标为 ( )
A.(-5,2) B.(2,5)
C.(5,-2) D.(-2,-5)
2.[2020·兰州] 若点A(-4,m-3),B(2n,1)关于x轴对称,则 ( )
A.m=2,n=0 B.m=2,n=-2
C.m=4,n=2 D.m=4,n=-2
3.点A关于y轴对称的点A1的坐标是(-2,-1),则点A关于x轴对称的点A2的坐标是 ( )
A.(-1,-2) B.(2,1)
C.(-2,1) D.(2,-1)
4.若△ABC的三个顶点的横坐标不变,纵坐标都乘-1,则所得三角形与原三角形的关系是 ( )
A.关于x轴对称
B.关于y轴对称
C.所得三角形是将原三角形沿x轴负方向平移1个单位长度得到的
D.所得三角形是将原三角形沿y轴负方向平移1个单位长度得到的
5.已知点P(a+1,2a-3)关于x轴对称的点在第一象限,则a的取值范围是 ( )
A.a> B.a>-1
C.-16.已知点P(a-1,-b+2)关于x轴对称与关于y轴对称的点的坐标相同,则a,b的值分别是 ( )
A.-1,2 B.-1,-2
C.-2,1 D.1,2
7.已知a,b,c为△ABC的三条边,点(a-c,a)与点(0,-b)关于x轴对称,则△ABC的形状为 .
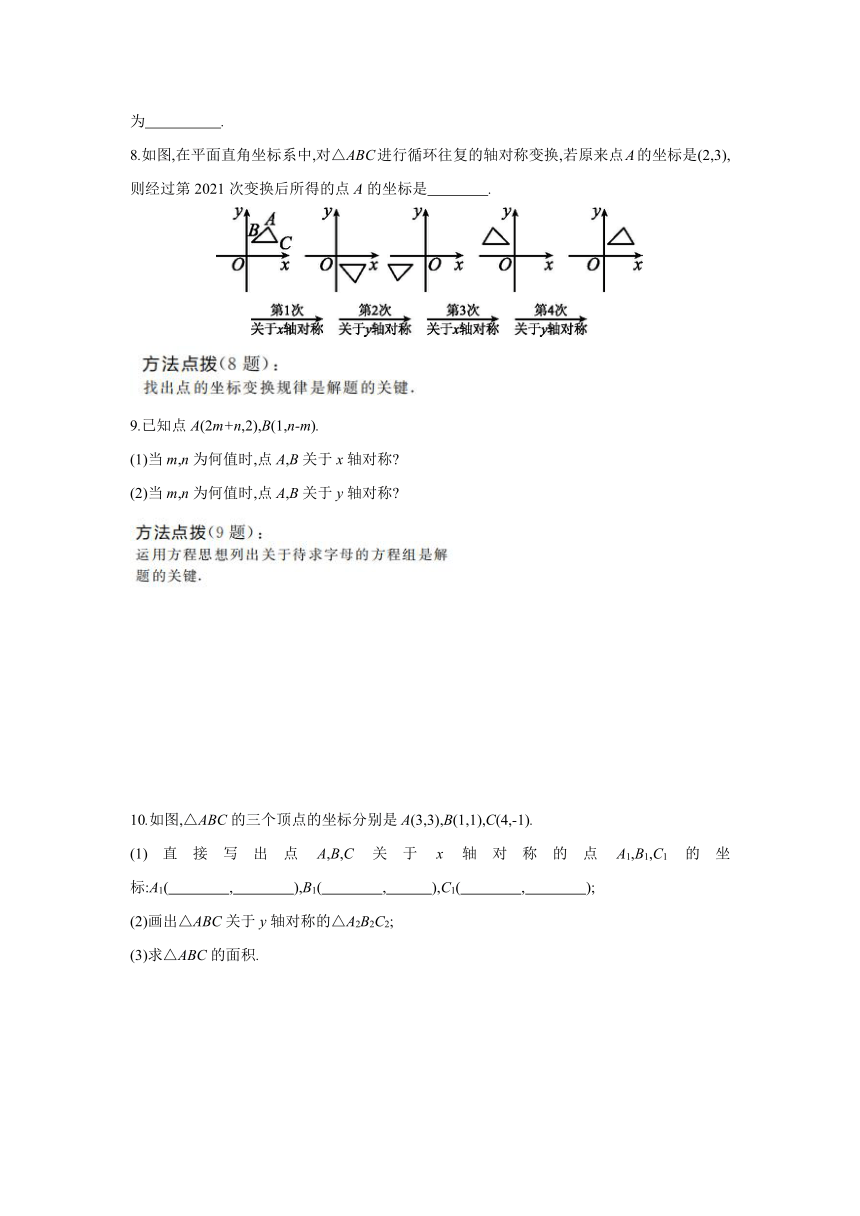
8.如图,在平面直角坐标系中,对△ABC进行循环往复的轴对称变换,若原来点A的坐标是(2,3),则经过第2021次变换后所得的点A的坐标是 .
9.已知点A(2m+n,2),B(1,n-m).
(1)当m,n为何值时,点A,B关于x轴对称
(2)当m,n为何值时,点A,B关于y轴对称
10.如图,△ABC的三个顶点的坐标分别是A(3,3),B(1,1),C(4,-1).
(1)直接写出点A,B,C关于x轴对称的点A1,B1,C1的坐标:A1( , ),B1( , ),C1( , );
(2)画出△ABC关于y轴对称的△A2B2C2;
(3)求△ABC的面积.
命题点 2 关于直线x=m或直线y=n对称的点的坐标
11.在平面直角坐标系中,已知在y轴与直线x=3之间有一点M(a,3).如图果该点关于直线x=3的对称点N的坐标为(5,3),那么a的值为 ( )
A.4 B.3 C.2 D.1
12.如图,在直角坐标系xOy中,直线y=1是△ABC的对称轴,已知点A的坐标是(4,4),则点B的坐标是 ( )
A.(4,-4) B.(-4,2)
C.(4,-2) D.(-2,4)
13.如图,在平面直角坐标系中,直线l过点M(3,0),且平行于y轴.
(1)如图果△ABC三个顶点的坐标分别是A(-2,0),B(-1,0),C(-1,2),△ABC关于y轴对称的图形是△A1B1C1,△A1B1C1关于直线l对称的图形是△A2B2C2,请直接写出△A2B2C2的三个顶点的坐标;
(2)如图果点P的坐标是(-a,0),其中a>0,点P关于y轴的对称点是P1,点P1关于直线l的对称点是P2,求PP2的长.
14.如图,在直角坐标系中,△ABO的各顶点的坐标分别为O(0,0),A(2a,0),B(0,-a),线段EF两端点的坐标分别为E(-m,a+1),F(-m,1)(其中2a>m>a>0),直线l∥y轴交x轴于点P(a,0),且线段EF与CD关于y轴对称,线段CD与MN关于直线l对称.
(1)求点M,N的坐标(用含m,a的式子表示);
(2)△ABO与△MFE能通过平移互相重合吗 若能通过平移互相重合,请你说出一种平移方案(平移的距离用含m,a的式子表示).
答案
1.B 2.B 3.B
4.A ∵纵坐标乘-1,
∴变化前后纵坐标互为相反数.
又∵横坐标不变,
∴所得三角形与原三角形关于x轴对称.
故选A.
5.C ∵点P(a+1,2a-3)关于x轴对称的点在第一象限,∴点P在第四象限.
∴
解得-1故选C.
6.D ∵点P关于x轴对称的点的坐标为(a-1,b-2),关于y轴对称的点的坐标为(1-a,-b+2),∴解得
故选D.
7.等边三角形 ∵点(a-c,a)与点(0,-b)关于x轴对称,
∴a-c=0,a=b.∴a=b=c.
∴△ABC是等边三角形.
故答案为等边三角形.
8.(2,-3) 由图可知,4次变换为一个循环组依次循环,
∵2021÷4=505……1,∴第2021次变换后所得的点A的坐标与第1次变换后所得的点A的坐标相同.
∵原来点A的坐标是(2,3),第1次变换后的坐标是(2,-3),
∴经过第2021次变换后所得的点A的坐标是(2,-3).
9.解:(1)∵点A(2m+n,2),B(1,n-m)关于x轴对称,
∴解得
(2)∵点A(2m+n,2),B(1,n-m)关于y轴对称,
∴解得
10.解:(1)3 -3 1 -1 4 1
(2)如图图.
(3)△ABC的面积为3×4-×2×2-×2×3-×1×4=5.
11.D ∵该点关于直线x=3的对称点N的坐标为(5,3),∴对称点到直线x=3的距离为5-3=2.
又∵点M(a,3)到直线x=3的距离为3-a,
∴3-a=2.∴a=1.
12.C 根据题意,得点A和点B关于直线y=1对称,它们到直线y=1的距离相等,都是3个单位长度,所以点B的坐标是(4,-2).
13.解:(1)△A2B2C2的三个顶点的坐标分别是A2(4,0),B2(5,0),C2(5,2).
(2)如图图①,若0又∵点P1与点P2关于直线x=3对称,
设P2(x,0),可得=3,即x=6-a.
∴P2(6-a,0),
则PP2=6-a-(-a)=6-a+a=6.
如图图②,若a>3,∵点P与点P1关于y轴对称,P(-a,0),∴P1(a,0).又∵点P1与点P2关于直线x=3对称,设P2(m,0),可得=3,即m=6-a.∴P2(6-a,0),则PP2=6-a-(-a)=6-a+a=6.
综上,PP2的长为6.
14.解:(1)∵线段EF与CD关于y轴对称,EF两端点的坐标分别为E(-m,a+1),F(-m,1),
∴C(m,a+1),D(m,1).
∴CD与直线l之间的距离为m-a.
∵线段CD与MN关于直线l对称,l与y轴之间的距离为a,
∴MN与y轴之间的距离为a-(m-a)=2a-m.
∴M(2a-m,a+1),N(2a-m,1).
(2)能.平移方案(不唯一):将△ABO向上平移(a+1)个单位长度后,再向左平移m个单位长度,即可与△MFE重合.
命题点 1 关于坐标轴对称的点的坐标
1.在平面直角坐标系中,点P(-2,5)关于y轴对称的点的坐标为 ( )
A.(-5,2) B.(2,5)
C.(5,-2) D.(-2,-5)
2.[2020·兰州] 若点A(-4,m-3),B(2n,1)关于x轴对称,则 ( )
A.m=2,n=0 B.m=2,n=-2
C.m=4,n=2 D.m=4,n=-2
3.点A关于y轴对称的点A1的坐标是(-2,-1),则点A关于x轴对称的点A2的坐标是 ( )
A.(-1,-2) B.(2,1)
C.(-2,1) D.(2,-1)
4.若△ABC的三个顶点的横坐标不变,纵坐标都乘-1,则所得三角形与原三角形的关系是 ( )
A.关于x轴对称
B.关于y轴对称
C.所得三角形是将原三角形沿x轴负方向平移1个单位长度得到的
D.所得三角形是将原三角形沿y轴负方向平移1个单位长度得到的
5.已知点P(a+1,2a-3)关于x轴对称的点在第一象限,则a的取值范围是 ( )
A.a> B.a>-1
C.-1
A.-1,2 B.-1,-2
C.-2,1 D.1,2
7.已知a,b,c为△ABC的三条边,点(a-c,a)与点(0,-b)关于x轴对称,则△ABC的形状为 .
8.如图,在平面直角坐标系中,对△ABC进行循环往复的轴对称变换,若原来点A的坐标是(2,3),则经过第2021次变换后所得的点A的坐标是 .
9.已知点A(2m+n,2),B(1,n-m).
(1)当m,n为何值时,点A,B关于x轴对称
(2)当m,n为何值时,点A,B关于y轴对称
10.如图,△ABC的三个顶点的坐标分别是A(3,3),B(1,1),C(4,-1).
(1)直接写出点A,B,C关于x轴对称的点A1,B1,C1的坐标:A1( , ),B1( , ),C1( , );
(2)画出△ABC关于y轴对称的△A2B2C2;
(3)求△ABC的面积.
命题点 2 关于直线x=m或直线y=n对称的点的坐标
11.在平面直角坐标系中,已知在y轴与直线x=3之间有一点M(a,3).如图果该点关于直线x=3的对称点N的坐标为(5,3),那么a的值为 ( )
A.4 B.3 C.2 D.1
12.如图,在直角坐标系xOy中,直线y=1是△ABC的对称轴,已知点A的坐标是(4,4),则点B的坐标是 ( )
A.(4,-4) B.(-4,2)
C.(4,-2) D.(-2,4)
13.如图,在平面直角坐标系中,直线l过点M(3,0),且平行于y轴.
(1)如图果△ABC三个顶点的坐标分别是A(-2,0),B(-1,0),C(-1,2),△ABC关于y轴对称的图形是△A1B1C1,△A1B1C1关于直线l对称的图形是△A2B2C2,请直接写出△A2B2C2的三个顶点的坐标;
(2)如图果点P的坐标是(-a,0),其中a>0,点P关于y轴的对称点是P1,点P1关于直线l的对称点是P2,求PP2的长.
14.如图,在直角坐标系中,△ABO的各顶点的坐标分别为O(0,0),A(2a,0),B(0,-a),线段EF两端点的坐标分别为E(-m,a+1),F(-m,1)(其中2a>m>a>0),直线l∥y轴交x轴于点P(a,0),且线段EF与CD关于y轴对称,线段CD与MN关于直线l对称.
(1)求点M,N的坐标(用含m,a的式子表示);
(2)△ABO与△MFE能通过平移互相重合吗 若能通过平移互相重合,请你说出一种平移方案(平移的距离用含m,a的式子表示).
答案
1.B 2.B 3.B
4.A ∵纵坐标乘-1,
∴变化前后纵坐标互为相反数.
又∵横坐标不变,
∴所得三角形与原三角形关于x轴对称.
故选A.
5.C ∵点P(a+1,2a-3)关于x轴对称的点在第一象限,∴点P在第四象限.
∴
解得-1
6.D ∵点P关于x轴对称的点的坐标为(a-1,b-2),关于y轴对称的点的坐标为(1-a,-b+2),∴解得
故选D.
7.等边三角形 ∵点(a-c,a)与点(0,-b)关于x轴对称,
∴a-c=0,a=b.∴a=b=c.
∴△ABC是等边三角形.
故答案为等边三角形.
8.(2,-3) 由图可知,4次变换为一个循环组依次循环,
∵2021÷4=505……1,∴第2021次变换后所得的点A的坐标与第1次变换后所得的点A的坐标相同.
∵原来点A的坐标是(2,3),第1次变换后的坐标是(2,-3),
∴经过第2021次变换后所得的点A的坐标是(2,-3).
9.解:(1)∵点A(2m+n,2),B(1,n-m)关于x轴对称,
∴解得
(2)∵点A(2m+n,2),B(1,n-m)关于y轴对称,
∴解得
10.解:(1)3 -3 1 -1 4 1
(2)如图图.
(3)△ABC的面积为3×4-×2×2-×2×3-×1×4=5.
11.D ∵该点关于直线x=3的对称点N的坐标为(5,3),∴对称点到直线x=3的距离为5-3=2.
又∵点M(a,3)到直线x=3的距离为3-a,
∴3-a=2.∴a=1.
12.C 根据题意,得点A和点B关于直线y=1对称,它们到直线y=1的距离相等,都是3个单位长度,所以点B的坐标是(4,-2).
13.解:(1)△A2B2C2的三个顶点的坐标分别是A2(4,0),B2(5,0),C2(5,2).
(2)如图图①,若0
设P2(x,0),可得=3,即x=6-a.
∴P2(6-a,0),
则PP2=6-a-(-a)=6-a+a=6.
如图图②,若a>3,∵点P与点P1关于y轴对称,P(-a,0),∴P1(a,0).又∵点P1与点P2关于直线x=3对称,设P2(m,0),可得=3,即m=6-a.∴P2(6-a,0),则PP2=6-a-(-a)=6-a+a=6.
综上,PP2的长为6.
14.解:(1)∵线段EF与CD关于y轴对称,EF两端点的坐标分别为E(-m,a+1),F(-m,1),
∴C(m,a+1),D(m,1).
∴CD与直线l之间的距离为m-a.
∵线段CD与MN关于直线l对称,l与y轴之间的距离为a,
∴MN与y轴之间的距离为a-(m-a)=2a-m.
∴M(2a-m,a+1),N(2a-m,1).
(2)能.平移方案(不唯一):将△ABO向上平移(a+1)个单位长度后,再向左平移m个单位长度,即可与△MFE重合.
