人教版数学八年级上册同步提优训练:13.3.1 第1课时 等腰三角形的性质(Word版含答案)
文档属性
| 名称 | 人教版数学八年级上册同步提优训练:13.3.1 第1课时 等腰三角形的性质(Word版含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 239.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-07-10 10:42:22 | ||
图片预览


文档简介
13.3.1 第1课时 等腰三角形的性质
命题点 1 等边对等角
1.在△ABC中,AB=AC,若∠B=72°,则∠A的度数为 ( )
A.72° B.45° C.36° D.30°
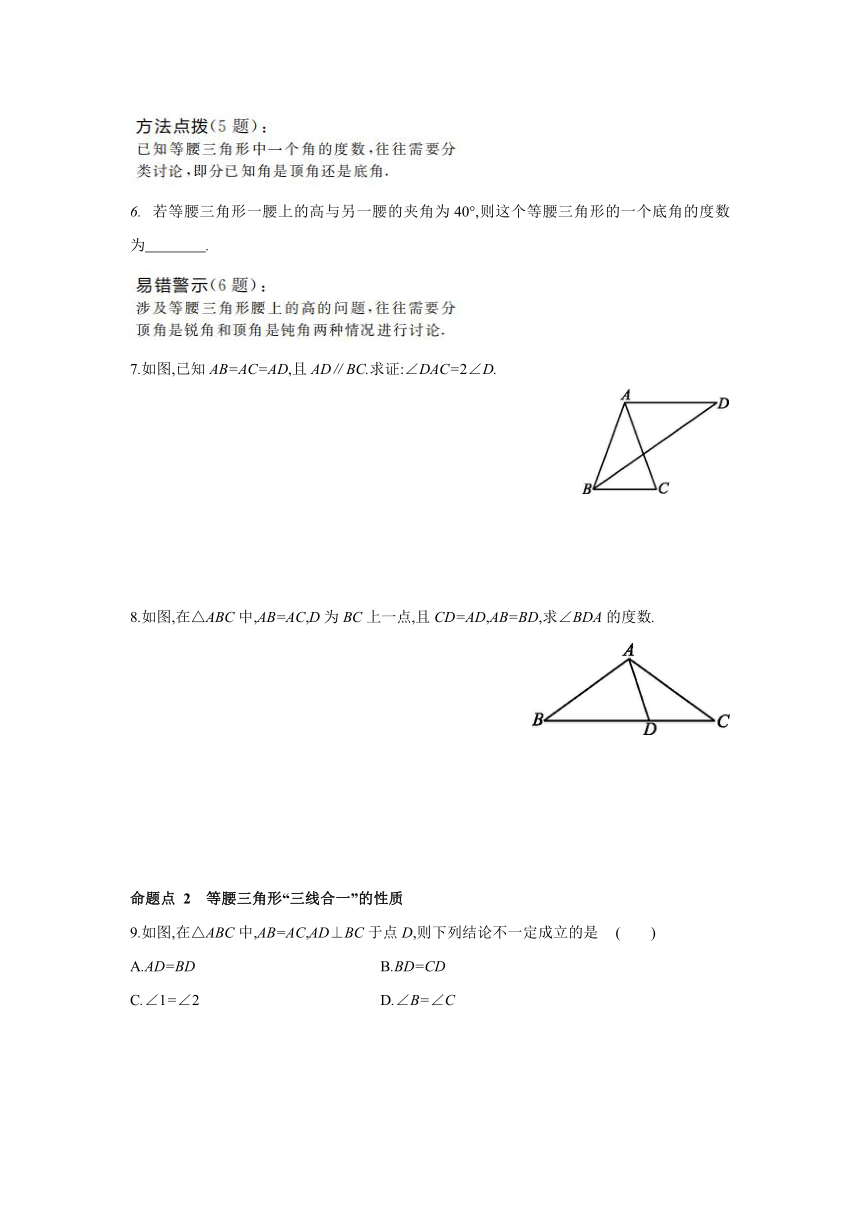
2.如图,在△ABC中,点D为边AC上一点,且AB=DB=DC,∠C=40°,则∠ABD的度数是 ( )
A.20° B.40° C.60° D.80°
3.如图,在△ABC中,AB=AC,∠A=40°,DE垂直平分AC,则∠BCD的度数为 ( )
A.20° B.30° C.40° D.50°
4.如图,在等腰三角形ABC中,AB=AC,∠A=40°,P是△ABC内一点,且∠1=∠2,则∠BPC的度数为 ( )
A.110° B.120° C.130° D.140°
若等腰三角形的一个角为42°,则它的顶角的度数为 .
若等腰三角形一腰上的高与另一腰的夹角为40°,则这个等腰三角形的一个底角的度数为 .
7.如图,已知AB=AC=AD,且AD∥BC.求证:∠DAC=2∠D.
8.如图,在△ABC中,AB=AC,D为BC上一点,且CD=AD,AB=BD,求∠BDA的度数.
命题点 2 等腰三角形“三线合一”的性质
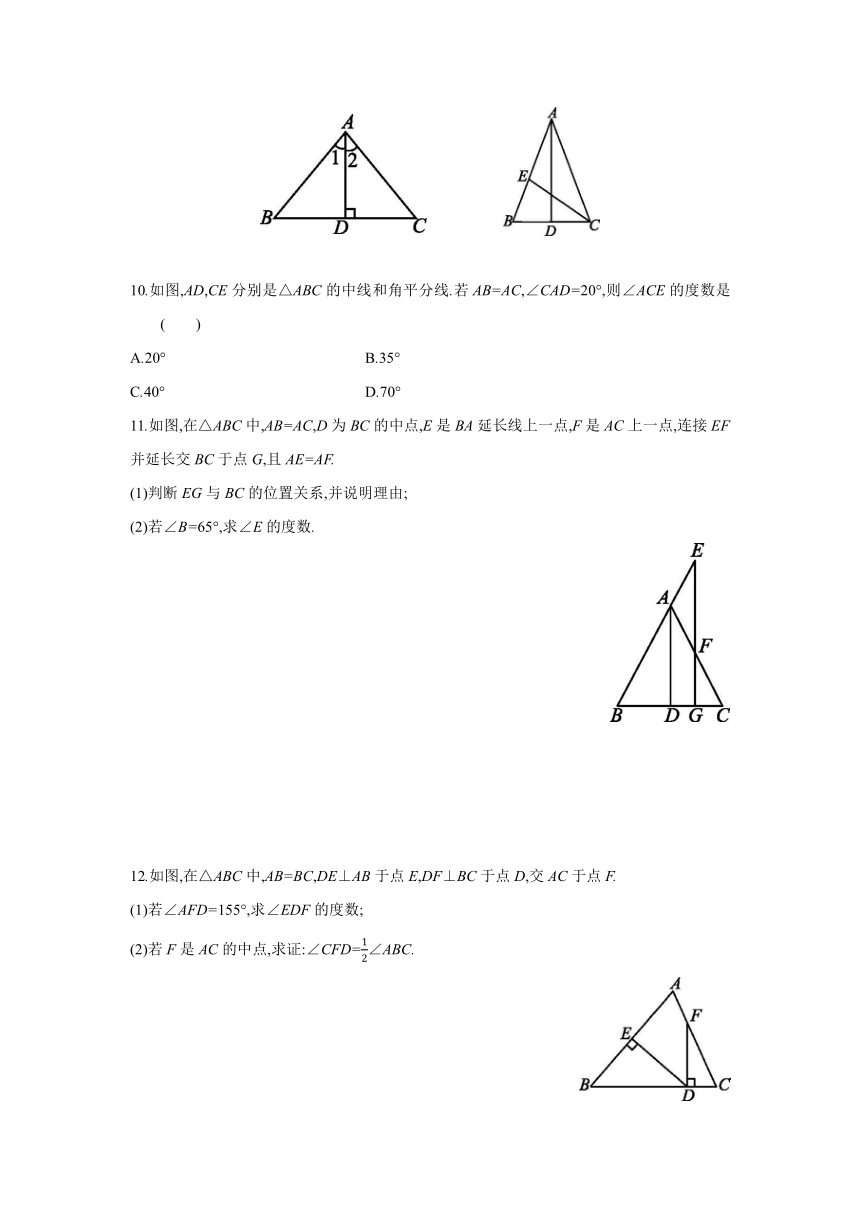
9.如图,在△ABC中,AB=AC,AD⊥BC于点D,则下列结论不一定成立的是 ( )
A.AD=BD B.BD=CD
C.∠1=∠2 D.∠B=∠C
10.如图,AD,CE分别是△ABC的中线和角平分线.若AB=AC,∠CAD=20°,则∠ACE的度数是 ( )
A.20° B.35°
C.40° D.70°
11.如图,在△ABC中,AB=AC,D为BC的中点,E是BA延长线上一点,F是AC上一点,连接EF并延长交BC于点G,且AE=AF.
(1)判断EG与BC的位置关系,并说明理由;
(2)若∠B=65°,求∠E的度数.
12.如图,在△ABC中,AB=BC,DE⊥AB于点E,DF⊥BC于点D,交AC于点F.
(1)若∠AFD=155°,求∠EDF的度数;
(2)若F是AC的中点,求证:∠CFD=∠ABC.
13.(1)如图,在△ABC中,∠BAC=90°,BA=CA,点D在BC上,且BD=BA,点E在BC的延长线上,且CE=CA,试求∠DAE的度数;
(2)如图果把(1)中的条件“BA=CA”去掉,其余条件不变,那么∠DAE的度数会改变吗 请说明理由;
(3)如图果把(1)中的条件“∠BAC=90°”改为“∠BAC>90°”,其余条件不变,那么∠DAE与∠BAC之间有什么数量关系
答案
1.C
2.A ∵DB=DC,∠C=40°,
∴∠DBC=∠C=40°.
∴∠BDC=180°-40°×2=100°.
∴∠BDA=80°.
∵AB=DB,∴∠A=80°.
∴∠ABD=180°-80°-80°=20°.
故选A.
3.B ∵AB=AC,∠A=40°,
∴∠ABC=∠ACB=70°.
∵DE垂直平分AC,∴AD=CD.
∴∠A=∠ACD=40°.
∴∠BCD=∠ACB-∠ACD=30°.故选B.
4.A ∵AB=AC,∠A=40°,
∴∠ABC=∠ACB=×(180°-40°)=70°.
∵∠1=∠2,
∴∠ACB=∠1+∠PCB=∠2+∠PCB=70°.
∴∠BPC=180°-(∠2+∠PCB)=110°.
5.42°或96° 该题分两种情况讨论:①42°的角为顶角时,顶角的度数是42°;②42°的角为底角时,顶角为180°-42°×2=96°.故答案为:42°或96°.
6.25°或65° 若这个三角形是锐角三角形,一腰上的高与另一腰的夹角为40°,则顶角是50°,因而底角是65°;
若这个三角形是钝角三角形,如图图,AB=AC,BD⊥AC,∠ABD=40°,故∠BAD=50°.所以∠C=25°.因此这个等腰三角形的一个底角的度数为25°或65°.
7.证明:∵AD∥BC,
∴∠DAC=∠C,∠D=∠DBC.
∵AB=AC,∴∠C=∠ABC.
∵AB=AD,∴∠D=∠ABD.
∴∠ABC=∠ABD+∠DBC=∠D+∠D=2∠D.∴∠DAC=∠C=∠ABC=2∠D.
8.解:∵AB=AC,∴∠B=∠C.
∵AB=BD,∴∠BAD=∠BDA.
∵CD=AD,∴∠C=∠CAD.
∴∠CAD=∠B.
∴∠BDA=∠C+∠CAD=2∠B.
∴∠BAD=2∠B.
∵∠BAD+∠CAD+∠B+∠C=180°,
∴5∠B=180°.
∴∠B=36°.
∴∠BDA=2∠B=72°.
9.A
10.B ∵AD是△ABC的中线,AB=AC,∠CAD=20°,∴∠CAB=2∠CAD=40°.
∴∠B=∠ACB=(180°-∠CAB)=70°.
∵CE是△ABC的角平分线,
∴∠ACE=∠ACB=35°.
11.解:(1)EG⊥BC.
理由:∵AB=AC,D为BC的中点,
∴AD⊥BC,AD平分∠BAC,∠B=∠C.
∴∠BAD=∠CAD=∠BAC.
∵AE=AF,∴∠E=∠AFE.
∵∠BAC=∠BAD+∠CAD=∠E+∠AFE,
∴∠E=∠BAD.
∴AD∥EG.∴EG⊥BC.
(2)∵∠B=∠C=65°,
∴∠BAC=180°-65°-65°=50°.
∴∠BAD=∠CAD=∠BAC=×50°=25°.
∴∠E=∠BAD=25°.
12.解:(1)∵∠AFD=155°,
∴∠DFC=180°-∠AFD=25°.
∵DF⊥BC,DE⊥AB,
∴∠FDC=∠AED=90°.
∴在Rt△FDC中,∠C=90°-25°=65°.
∵AB=BC,
∴∠A=∠C=65°.
∴∠EDF=360°-65°-155°-90°=50°.
(2)证明:如图图,连接BF.
∵AB=BC,F是AC的中点,
∴BF⊥AC,∠ABF=∠CBF=∠ABC.
∴∠CFD+∠BFD=90°.
∵DF⊥BC,∴∠CBF+∠BFD=90°.
∴∠CFD=∠CBF.
∴∠CFD=∠ABC.
13.解:(1)∵BA=CA,∠BAC=90°,
∴∠B=∠ACB=45°.
∵BD=BA,∴∠BAD=∠BDA=67.5°.
∵CE=CA,∴∠CAE=∠E=∠ACB=22.5°.
∴∠DAE=∠BDA-∠E=67.5°-22.5°=45°.
(2)不会改变.理由:设∠CAE=m.
∵CA=CE,∴∠E=∠CAE=m.
∴∠ACB=∠CAE+∠E=2m.
∵在△ABC中,∠BAC=90°,
∴∠B=90°-∠ACB=90°-2m.
∵BD=BA,
∴∠BAD=∠BDA=(180°-∠B)=m+45°.
∴∠DAE=∠BDA-∠E=m+45°-m=45°.
(3)设∠CAE=x,∠BAD=y,则∠E=∠CAE=x,∠BDA=∠BAD=y.
∴∠DAE=∠BDA-∠E=y-x.
又∵∠BAC=∠BAD+∠DAE-∠CAE=2y-2x,∴∠DAE=∠BAC.
命题点 1 等边对等角
1.在△ABC中,AB=AC,若∠B=72°,则∠A的度数为 ( )
A.72° B.45° C.36° D.30°
2.如图,在△ABC中,点D为边AC上一点,且AB=DB=DC,∠C=40°,则∠ABD的度数是 ( )
A.20° B.40° C.60° D.80°
3.如图,在△ABC中,AB=AC,∠A=40°,DE垂直平分AC,则∠BCD的度数为 ( )
A.20° B.30° C.40° D.50°
4.如图,在等腰三角形ABC中,AB=AC,∠A=40°,P是△ABC内一点,且∠1=∠2,则∠BPC的度数为 ( )
A.110° B.120° C.130° D.140°
若等腰三角形的一个角为42°,则它的顶角的度数为 .
若等腰三角形一腰上的高与另一腰的夹角为40°,则这个等腰三角形的一个底角的度数为 .
7.如图,已知AB=AC=AD,且AD∥BC.求证:∠DAC=2∠D.
8.如图,在△ABC中,AB=AC,D为BC上一点,且CD=AD,AB=BD,求∠BDA的度数.
命题点 2 等腰三角形“三线合一”的性质
9.如图,在△ABC中,AB=AC,AD⊥BC于点D,则下列结论不一定成立的是 ( )
A.AD=BD B.BD=CD
C.∠1=∠2 D.∠B=∠C
10.如图,AD,CE分别是△ABC的中线和角平分线.若AB=AC,∠CAD=20°,则∠ACE的度数是 ( )
A.20° B.35°
C.40° D.70°
11.如图,在△ABC中,AB=AC,D为BC的中点,E是BA延长线上一点,F是AC上一点,连接EF并延长交BC于点G,且AE=AF.
(1)判断EG与BC的位置关系,并说明理由;
(2)若∠B=65°,求∠E的度数.
12.如图,在△ABC中,AB=BC,DE⊥AB于点E,DF⊥BC于点D,交AC于点F.
(1)若∠AFD=155°,求∠EDF的度数;
(2)若F是AC的中点,求证:∠CFD=∠ABC.
13.(1)如图,在△ABC中,∠BAC=90°,BA=CA,点D在BC上,且BD=BA,点E在BC的延长线上,且CE=CA,试求∠DAE的度数;
(2)如图果把(1)中的条件“BA=CA”去掉,其余条件不变,那么∠DAE的度数会改变吗 请说明理由;
(3)如图果把(1)中的条件“∠BAC=90°”改为“∠BAC>90°”,其余条件不变,那么∠DAE与∠BAC之间有什么数量关系
答案
1.C
2.A ∵DB=DC,∠C=40°,
∴∠DBC=∠C=40°.
∴∠BDC=180°-40°×2=100°.
∴∠BDA=80°.
∵AB=DB,∴∠A=80°.
∴∠ABD=180°-80°-80°=20°.
故选A.
3.B ∵AB=AC,∠A=40°,
∴∠ABC=∠ACB=70°.
∵DE垂直平分AC,∴AD=CD.
∴∠A=∠ACD=40°.
∴∠BCD=∠ACB-∠ACD=30°.故选B.
4.A ∵AB=AC,∠A=40°,
∴∠ABC=∠ACB=×(180°-40°)=70°.
∵∠1=∠2,
∴∠ACB=∠1+∠PCB=∠2+∠PCB=70°.
∴∠BPC=180°-(∠2+∠PCB)=110°.
5.42°或96° 该题分两种情况讨论:①42°的角为顶角时,顶角的度数是42°;②42°的角为底角时,顶角为180°-42°×2=96°.故答案为:42°或96°.
6.25°或65° 若这个三角形是锐角三角形,一腰上的高与另一腰的夹角为40°,则顶角是50°,因而底角是65°;
若这个三角形是钝角三角形,如图图,AB=AC,BD⊥AC,∠ABD=40°,故∠BAD=50°.所以∠C=25°.因此这个等腰三角形的一个底角的度数为25°或65°.
7.证明:∵AD∥BC,
∴∠DAC=∠C,∠D=∠DBC.
∵AB=AC,∴∠C=∠ABC.
∵AB=AD,∴∠D=∠ABD.
∴∠ABC=∠ABD+∠DBC=∠D+∠D=2∠D.∴∠DAC=∠C=∠ABC=2∠D.
8.解:∵AB=AC,∴∠B=∠C.
∵AB=BD,∴∠BAD=∠BDA.
∵CD=AD,∴∠C=∠CAD.
∴∠CAD=∠B.
∴∠BDA=∠C+∠CAD=2∠B.
∴∠BAD=2∠B.
∵∠BAD+∠CAD+∠B+∠C=180°,
∴5∠B=180°.
∴∠B=36°.
∴∠BDA=2∠B=72°.
9.A
10.B ∵AD是△ABC的中线,AB=AC,∠CAD=20°,∴∠CAB=2∠CAD=40°.
∴∠B=∠ACB=(180°-∠CAB)=70°.
∵CE是△ABC的角平分线,
∴∠ACE=∠ACB=35°.
11.解:(1)EG⊥BC.
理由:∵AB=AC,D为BC的中点,
∴AD⊥BC,AD平分∠BAC,∠B=∠C.
∴∠BAD=∠CAD=∠BAC.
∵AE=AF,∴∠E=∠AFE.
∵∠BAC=∠BAD+∠CAD=∠E+∠AFE,
∴∠E=∠BAD.
∴AD∥EG.∴EG⊥BC.
(2)∵∠B=∠C=65°,
∴∠BAC=180°-65°-65°=50°.
∴∠BAD=∠CAD=∠BAC=×50°=25°.
∴∠E=∠BAD=25°.
12.解:(1)∵∠AFD=155°,
∴∠DFC=180°-∠AFD=25°.
∵DF⊥BC,DE⊥AB,
∴∠FDC=∠AED=90°.
∴在Rt△FDC中,∠C=90°-25°=65°.
∵AB=BC,
∴∠A=∠C=65°.
∴∠EDF=360°-65°-155°-90°=50°.
(2)证明:如图图,连接BF.
∵AB=BC,F是AC的中点,
∴BF⊥AC,∠ABF=∠CBF=∠ABC.
∴∠CFD+∠BFD=90°.
∵DF⊥BC,∴∠CBF+∠BFD=90°.
∴∠CFD=∠CBF.
∴∠CFD=∠ABC.
13.解:(1)∵BA=CA,∠BAC=90°,
∴∠B=∠ACB=45°.
∵BD=BA,∴∠BAD=∠BDA=67.5°.
∵CE=CA,∴∠CAE=∠E=∠ACB=22.5°.
∴∠DAE=∠BDA-∠E=67.5°-22.5°=45°.
(2)不会改变.理由:设∠CAE=m.
∵CA=CE,∴∠E=∠CAE=m.
∴∠ACB=∠CAE+∠E=2m.
∵在△ABC中,∠BAC=90°,
∴∠B=90°-∠ACB=90°-2m.
∵BD=BA,
∴∠BAD=∠BDA=(180°-∠B)=m+45°.
∴∠DAE=∠BDA-∠E=m+45°-m=45°.
(3)设∠CAE=x,∠BAD=y,则∠E=∠CAE=x,∠BDA=∠BAD=y.
∴∠DAE=∠BDA-∠E=y-x.
又∵∠BAC=∠BAD+∠DAE-∠CAE=2y-2x,∴∠DAE=∠BAC.
