山东省淄博市周村区2021-2022学年六年级下学期期末数学试题(word版含答案)
文档属性
| 名称 | 山东省淄博市周村区2021-2022学年六年级下学期期末数学试题(word版含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 1.3MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 鲁教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-07-09 22:06:19 | ||
图片预览


文档简介
六年级数学试题
一、选择题(在每小题给出的四个选项中,只有一个是正确的,请把正确的选项填在题后的括号内,每小题5分,共60分)
1.要反映我区六月份每天最高气温的变化趋势,最宜采用( )
A.扇形图 B.条形图 C.折线图 D.直方图
2.若,则的余角的度数为( )
A. B. C. D.
3.计算的结果正确的是( )
A. B. C. D.
4.下列调查中,不适合用抽样调查方式的是( )
A.调查某电视剧的收视率 B.调查某种品牌插座的使用寿命
C.调查孝妇河的水质情况 D.调查疫情期间某超市员工的体温情况
5.人的头发粗细各异,普通头发的直径是0.00008米,0.00008用科学记数法表示为( )
A. B. C. D.
6.下列运算,正确的是( )
A. B.
C. D.
7.如图,若AB,CD相交于点O,过点O作,则下列结论不正确的是( )
A.与互为余角 B.与互为余角
C.与互为补角 D.与是对顶角
8.下列条件:①,②,③,其中能判断的是( )
A.① B.①③ C.②③ D.①②③
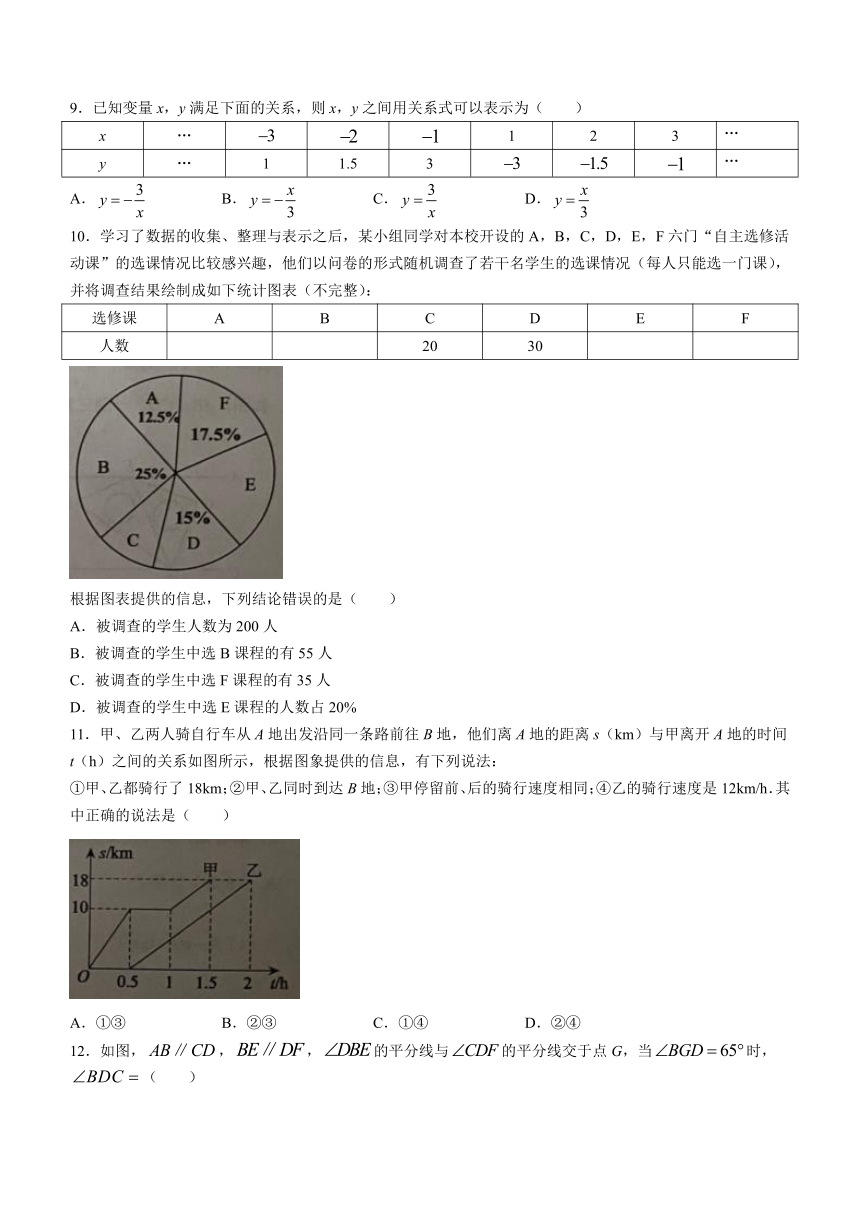
9.已知变量x,y满足下面的关系,则x,y之间用关系式可以表示为( )
x … 1 2 3 …
y … 1 1.5 3 …
A. B. C. D.
10.学习了数据的收集、整理与表示之后,某小组同学对本校开设的A,B,C,D,E,F六门“自主选修活动课”的选课情况比较感兴趣,他们以问卷的形式随机调查了若干名学生的选课情况(每人只能选一门课),并将调查结果绘制成如下统计图表(不完整):
选修课 A B C D E F
人数 20 30
根据图表提供的信息,下列结论错误的是( )
A.被调查的学生人数为200人
B.被调查的学生中选B课程的有55人
C.被调查的学生中选F课程的有35人
D.被调查的学生中选E课程的人数占20%
11.甲、乙两人骑自行车从A地出发沿同一条路前往B地,他们离A地的距离s(km)与甲离开A地的时间t(h)之间的关系如图所示,根据图象提供的信息,有下列说法:
①甲、乙都骑行了18km;②甲、乙同时到达B地;③甲停留前、后的骑行速度相同;④乙的骑行速度是12km/h.其中正确的说法是( )
A.①③ B.②③ C.①④ D.②④
12.如图,,,的平分线与的平分线交于点G,当时,( )
A.65° B.60° C.55° D.50°
二、填空题:请将最终结果填入题中的横线上(每小题4分,共20分)
13.计算的结果为__________.
14.如果一个角的补角是这个角的3倍,那么这个角的度数是__________°.
15.若,则的值为__________.
16.如图,,一副三角尺按如图所示放置,,则__________°.
17.杨辉是我国南宋时期杰出的数学家,此图是杨辉在其著作《详解九章算法》里面的一张图,即“杨辉三角”,图中给出了七行数字,例如,第4行中从左边数第2个数是3,照此规律一直排列下去,那么第n行中的所有数之和为__________.
三、解答题:要写出必要的文字说明或演算步骤(共70分)
18.(8分)计算:
(1)
(2)
19.(8分)先化简,再求值:,其中.
20.(10分)如图1,从边长为a的正方形纸片中剪去一个边长为b的小正方形,再沿着虚线剪开,把剪成的两张纸片拼成如图2所示的长方形.
(1)设图1中的阴影部分面积为,图2中的阴影部分面积为,请用含有a,b的代数式表示,则__________,__________;
(2)请写出上述剪拼过程所揭示的乘法公式:__________;
(3)请你利用(2)中的公式计算:.
21.(10分)如图,在四边形ABCD中,,连接BD,点E在边BC上,点F在边CD上,且.
(1)求证:;
(2)若BD平分,,,求的度数.
22.(10分)某综合实践小组的同学对本校六年级学生课外阅读最喜爱的图书种类进行了调查.根据问卷调查(每个被调查的学生只能选择其中一项)的结果绘制了如下两幅统计图(不完整):
根据以上信息,回答下列问题:
(1)这次被调查的学生共有__________人;
(2)请将图1补充完整并在图上标出数据;
(3)图2中,__________,“科普类”部分扇形的圆心角是__________°;
(4)若该校六年级共有学生320人,根据调查结果估计此年级最喜欢“文学类”图书的学生约有__________人.
23.(12分)甲乙两地相距300千米,一辆货车和一辆轿车先后从甲地出发向乙地,轿车比货车晚出发1.5小时,如图,线段OA表示货车离甲地的距离y(千米)与时间x(小时)之间的关系;折线BCD表示轿车离甲地的距离y(千米)与时间x(时)之间的关系,请根据图象解答下列问题:
(1)请直接写出点B所对应的数;
(2)轿车到达乙地时,求货车与甲地的距离;
(3)轿车出发多长时间追上货车?
24.(12分)如图,已知,,点C是射线AN上一动点(不与点A重合),PB,PD分别平分和,交射线AN于点B,D.
(1)求的度数;
(2)当点C运动到使时,求的度数;
(3)在点C运动过程中,与之间是否存在一定的数量关系?若存在,请写出它们之间的数量关系,并说明理由;若不存在,请举出反例.
六年级数学参考答案
一、选择题:本题共12小题,每小题5分,共60分
题号 1 2 3 4 5 6 7 8 9 10 11 12
答案 C A A D B D C B A B C D
二、填空题:每小题4分,共20分.
13.; 14.45; 15.25; 16.35; 17.
三、解答题:8个小题,共70分.
18.(8分)
(1)
(2)
19.(8分)解:原式
当时,原式
20.(10分)
(1),
(2)或均可;
(3)
21.(10分)
(1)证明:∵,∴.∵,∴.∴
(2)解:∵,
∴,.
∵,,∴,.
∵DB平分,∴.
∴.∵,∴
∵,∴.
22.(10分)
(1)80.
(2)如图所示.
(3)20,90.
(4)128.
23.(12分)
解:(1)点B所对应的数是1.5;
(2)根据图象可知,货车速度是(千米/小时),(千米),
∴轿车到达乙地时,货车与甲地的距离是270千米;
(3)∵轿车在CD段的速度是:(千米/小时),
设轿车出发x小时追上货车,∴
解得,
∴轿车出发2.4小时追上货车.
24.(12分)
解:(1)∵,∴,∵,∴,
∵PB,PD分别平分和,∴,,
∴;
(2)∵,∴,∵,
∴,∴,
由(1)得:,,
∴,∴;
(3)存在,,
理由如下:∵,
∴,,∵PD平分,∴,∴
一、选择题(在每小题给出的四个选项中,只有一个是正确的,请把正确的选项填在题后的括号内,每小题5分,共60分)
1.要反映我区六月份每天最高气温的变化趋势,最宜采用( )
A.扇形图 B.条形图 C.折线图 D.直方图
2.若,则的余角的度数为( )
A. B. C. D.
3.计算的结果正确的是( )
A. B. C. D.
4.下列调查中,不适合用抽样调查方式的是( )
A.调查某电视剧的收视率 B.调查某种品牌插座的使用寿命
C.调查孝妇河的水质情况 D.调查疫情期间某超市员工的体温情况
5.人的头发粗细各异,普通头发的直径是0.00008米,0.00008用科学记数法表示为( )
A. B. C. D.
6.下列运算,正确的是( )
A. B.
C. D.
7.如图,若AB,CD相交于点O,过点O作,则下列结论不正确的是( )
A.与互为余角 B.与互为余角
C.与互为补角 D.与是对顶角
8.下列条件:①,②,③,其中能判断的是( )
A.① B.①③ C.②③ D.①②③
9.已知变量x,y满足下面的关系,则x,y之间用关系式可以表示为( )
x … 1 2 3 …
y … 1 1.5 3 …
A. B. C. D.
10.学习了数据的收集、整理与表示之后,某小组同学对本校开设的A,B,C,D,E,F六门“自主选修活动课”的选课情况比较感兴趣,他们以问卷的形式随机调查了若干名学生的选课情况(每人只能选一门课),并将调查结果绘制成如下统计图表(不完整):
选修课 A B C D E F
人数 20 30
根据图表提供的信息,下列结论错误的是( )
A.被调查的学生人数为200人
B.被调查的学生中选B课程的有55人
C.被调查的学生中选F课程的有35人
D.被调查的学生中选E课程的人数占20%
11.甲、乙两人骑自行车从A地出发沿同一条路前往B地,他们离A地的距离s(km)与甲离开A地的时间t(h)之间的关系如图所示,根据图象提供的信息,有下列说法:
①甲、乙都骑行了18km;②甲、乙同时到达B地;③甲停留前、后的骑行速度相同;④乙的骑行速度是12km/h.其中正确的说法是( )
A.①③ B.②③ C.①④ D.②④
12.如图,,,的平分线与的平分线交于点G,当时,( )
A.65° B.60° C.55° D.50°
二、填空题:请将最终结果填入题中的横线上(每小题4分,共20分)
13.计算的结果为__________.
14.如果一个角的补角是这个角的3倍,那么这个角的度数是__________°.
15.若,则的值为__________.
16.如图,,一副三角尺按如图所示放置,,则__________°.
17.杨辉是我国南宋时期杰出的数学家,此图是杨辉在其著作《详解九章算法》里面的一张图,即“杨辉三角”,图中给出了七行数字,例如,第4行中从左边数第2个数是3,照此规律一直排列下去,那么第n行中的所有数之和为__________.
三、解答题:要写出必要的文字说明或演算步骤(共70分)
18.(8分)计算:
(1)
(2)
19.(8分)先化简,再求值:,其中.
20.(10分)如图1,从边长为a的正方形纸片中剪去一个边长为b的小正方形,再沿着虚线剪开,把剪成的两张纸片拼成如图2所示的长方形.
(1)设图1中的阴影部分面积为,图2中的阴影部分面积为,请用含有a,b的代数式表示,则__________,__________;
(2)请写出上述剪拼过程所揭示的乘法公式:__________;
(3)请你利用(2)中的公式计算:.
21.(10分)如图,在四边形ABCD中,,连接BD,点E在边BC上,点F在边CD上,且.
(1)求证:;
(2)若BD平分,,,求的度数.
22.(10分)某综合实践小组的同学对本校六年级学生课外阅读最喜爱的图书种类进行了调查.根据问卷调查(每个被调查的学生只能选择其中一项)的结果绘制了如下两幅统计图(不完整):
根据以上信息,回答下列问题:
(1)这次被调查的学生共有__________人;
(2)请将图1补充完整并在图上标出数据;
(3)图2中,__________,“科普类”部分扇形的圆心角是__________°;
(4)若该校六年级共有学生320人,根据调查结果估计此年级最喜欢“文学类”图书的学生约有__________人.
23.(12分)甲乙两地相距300千米,一辆货车和一辆轿车先后从甲地出发向乙地,轿车比货车晚出发1.5小时,如图,线段OA表示货车离甲地的距离y(千米)与时间x(小时)之间的关系;折线BCD表示轿车离甲地的距离y(千米)与时间x(时)之间的关系,请根据图象解答下列问题:
(1)请直接写出点B所对应的数;
(2)轿车到达乙地时,求货车与甲地的距离;
(3)轿车出发多长时间追上货车?
24.(12分)如图,已知,,点C是射线AN上一动点(不与点A重合),PB,PD分别平分和,交射线AN于点B,D.
(1)求的度数;
(2)当点C运动到使时,求的度数;
(3)在点C运动过程中,与之间是否存在一定的数量关系?若存在,请写出它们之间的数量关系,并说明理由;若不存在,请举出反例.
六年级数学参考答案
一、选择题:本题共12小题,每小题5分,共60分
题号 1 2 3 4 5 6 7 8 9 10 11 12
答案 C A A D B D C B A B C D
二、填空题:每小题4分,共20分.
13.; 14.45; 15.25; 16.35; 17.
三、解答题:8个小题,共70分.
18.(8分)
(1)
(2)
19.(8分)解:原式
当时,原式
20.(10分)
(1),
(2)或均可;
(3)
21.(10分)
(1)证明:∵,∴.∵,∴.∴
(2)解:∵,
∴,.
∵,,∴,.
∵DB平分,∴.
∴.∵,∴
∵,∴.
22.(10分)
(1)80.
(2)如图所示.
(3)20,90.
(4)128.
23.(12分)
解:(1)点B所对应的数是1.5;
(2)根据图象可知,货车速度是(千米/小时),(千米),
∴轿车到达乙地时,货车与甲地的距离是270千米;
(3)∵轿车在CD段的速度是:(千米/小时),
设轿车出发x小时追上货车,∴
解得,
∴轿车出发2.4小时追上货车.
24.(12分)
解:(1)∵,∴,∵,∴,
∵PB,PD分别平分和,∴,,
∴;
(2)∵,∴,∵,
∴,∴,
由(1)得:,,
∴,∴;
(3)存在,,
理由如下:∵,
∴,,∵PD平分,∴,∴
同课章节目录
