人教版必修二5.2 运动的合成与分解 课件(29张PPT)
文档属性
| 名称 | 人教版必修二5.2 运动的合成与分解 课件(29张PPT) |  | |
| 格式 | ppt | ||
| 文件大小 | 3.4MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(2019) | ||
| 科目 | 物理 | ||
| 更新时间 | 2022-07-10 07:56:37 | ||
图片预览






文档简介
(共29张PPT)
2
运动的合成和分解
讨论
若人在河中始终保持头朝正前方游向对岸,你认为他会在对岸的正前方到达,还是会偏向上游或下游?为什么?
对于较复杂的运动,可以通过运动分解进行处理。达到简化模型的效果。
讨论
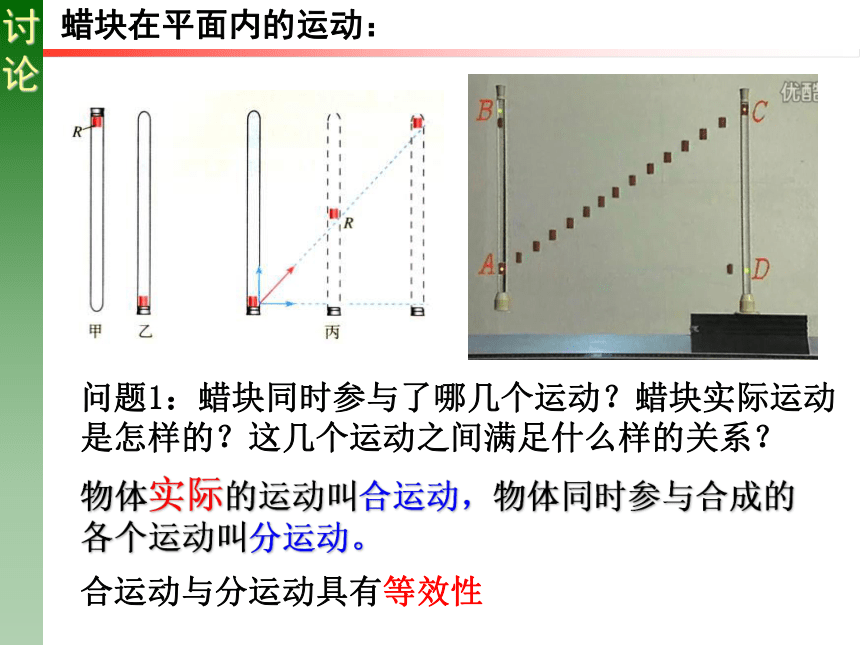
蜡块在平面内的运动:
问题1:蜡块同时参与了哪几个运动?蜡块实际运动是怎样的?这几个运动之间满足什么样的关系?
物体实际的运动叫合运动,物体同时参与合成的各个运动叫分运动。
合运动与分运动具有等效性
讨论
a
a1
a2
运动的合成与分解是指 x、v、 a 的合成与分解。
v1
v2
v
A
B
x
x1
x2
分速度
分速度
合速度
分加速度
合加速度
位移的合成
速度的合成
加速度的合成
分加速度
合位移
分位移
分位移
运动的合成是惟一的,而运动的分解不是惟一的,通常按运动所产生的实际效果分解。
讨论
蜡块在平面内的运动
问题2:合运动与分运动所用的时间有什么关系?
合运动与分运动具有等时性
讨论
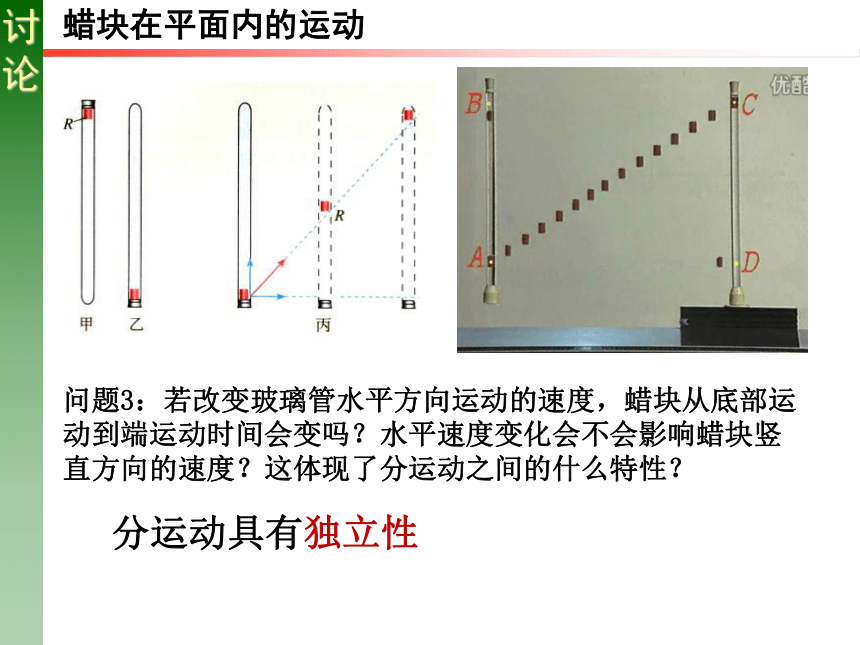
蜡块在平面内的运动
问题3:若改变玻璃管水平方向运动的速度,蜡块从底部运动到端运动时间会变吗?水平速度变化会不会影响蜡块竖直方向的速度?这体现了分运动之间的什么特性?
分运动具有独立性
讨论
讨论
x
y
蜡块运动的轨迹:
x = vx t
y = vy t
消去时间t:
蜡块相对于黑板的运动轨迹是过原点的一条直线
理论分析:
讨论
x
y
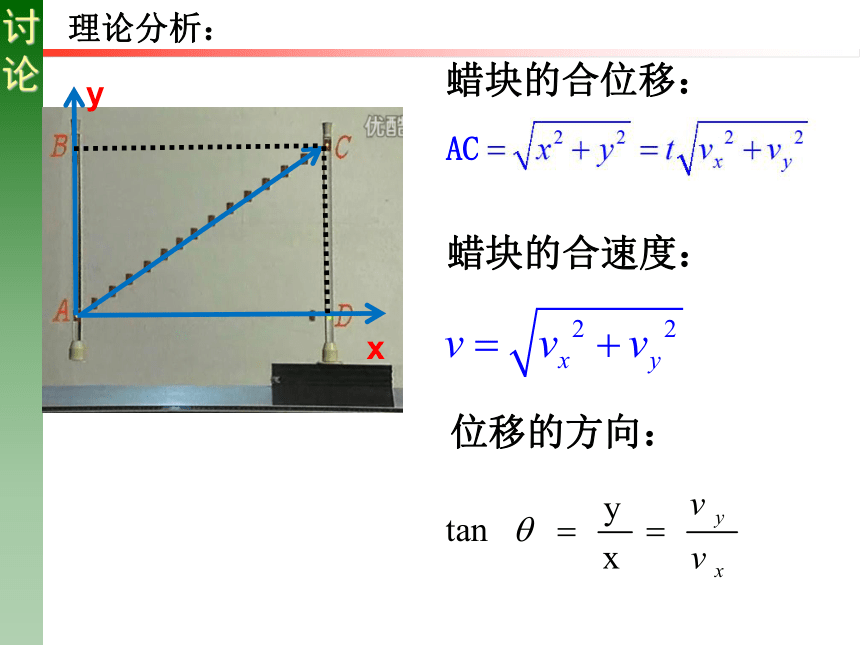
理论分析:
蜡块的合位移:
位移的方向:
蜡块的合速度:
AC
讨论
物体实际的运动叫合运动,物体同时参与合成的各个运动叫分运动。由分运动求合运动的过程,叫做运动的合成;由合运动求分运动的过程,叫做运动的分解。运动的合成与分解遵从矢量运算法则(平行四边形定则)。
合运动与分运动的关系:
2.合运动与分运动具有等时性
3.分运动具有独立性
1.合运动与分运动具有等效性
讨论
如果红蜡块在竖直方向上的分运动是匀速直线运动,在水平方向上的分运动是匀加速直线运动,合运动的轨迹是什么样的?
如果两个方向上的分运动的都是匀加速直线运动,合运动的轨迹又是什么样的?
两个直线运动合成的合运动一定是直线运动吗?
讨论
蜡块在平面内的运动
问题4:蜡块实际运动是怎样的?你可以怎么处理这个复杂的运动?
问题5:如何将曲线运动进行分解?各分运动分别做什么样的运动?物体做曲线运动的原因是什么?
y
x
讨论
蜡块在平面内的运动
问题6:若已知竖直方向速度为Vy,水平方向加速度为a,能否算出物体的运动轨迹?
y
x
问题7:能否求出物体在t时刻的位移、速度及速度的方向?
讨论
1.关于运动的合成,下列说法中正确的是 ( )
A.合运动的速度一定比每一个分运动的速度大
B.两个速度不等的匀速直线运动的合运动,一 定是匀速直线运动
C.两个分运动是直线运动的合运动,一定是直线运动
D.两个分运动的时间,一定与它们的合运动的时间相等
讨论
2.降落伞在下落一定时间后的运动是匀速的。无风时某跳伞员竖直下落,着地时的速度是4m/s。现在有风,风可以使他以3m/s的速度沿水平方向向东运动,他将以多大的速度着地?
讨论
3、玻璃生产线上,宽9 m的成型玻璃板以2 m/s的速度连续不断地向前行进,在切割工序处,金刚钻的走刀速度为10 m/s,为了使割下的玻璃板都成规定尺寸的矩形,金刚钻割刀的轨道应如何控制 切割一次的时间多长
01
练习
02
思考
03
实践
课后作业
完成课后练习
感受电场的存在
电场的特点
分运动的位置,位移,速度,加速度
合运动的位置,位移,速度,加速度
运动的合成
运动的分解
遵循平行四边形定则
独立,等时,等效
力的作用效果相同
分力
合力
力的合成
平行四边形定则
以两个共点力为邻边作平行四边形,这两个邻边之间的对角线就表示合力的大小和方向
复习回顾
运动的作用效果相同
分运动
合运动
运动的合成
平行四边形定则
以两个共点运动为邻边作平行四边形,这两个邻边之间的对角线就表示合运动的大小和方向
知识推广
运动的合成与分解专题
【例题1】一船准备渡河,已知水流速度为v0=3m/s,船在静水中的航速为v’ =5m/s,河宽200m则:
①要使船能够垂直地渡过河去,那么应向何方划船?渡河时间是多少?
②要使船能在最短时间内渡河,应向何方划船?能否求出船到达河岸时的位置?
渡河问题
【例题2】宽300米,河水流速3m/s,船在静水中的航速为1m/s,则该船渡河的最短时间为 ,渡河的最短位移为 。
【答案】300 s, 900m
【例题3】有一小船正在渡河,如图所示,在离对岸30m时,其下游40m处有一危险水域,假若水流速度为5m/s,为了使小船在危险水域之前到达对岸,那么从现在起,小船相对于静水的最小速度应是多大?方向如何?
30m
40m
危险区
【例题4】如图所示,纤绳以恒定速率v沿水平方向通过定滑轮牵引小船靠岸,当纤绳与水面夹角为θ时,船靠岸的速度是 ,若使船匀速靠岸,则纤绳的速度是 。(填:匀速、加速、减速)
“绳+物”问题
①沿绳方向直线运动
②以定滑轮为圆心垂直绳的转动
寻找分运动效果
“绳+物”问题
【问题综述】 此类问题的关键是:
1.准确判断谁是合运动,谁是分运动;实际运动是合运动。
2.根据运动效果寻找分运动;
3.一般情况下,分运动表现在:
①沿绳方向的伸长或收缩运动;
②垂直于绳方向的旋转运动。
4.根据运动效果认真做好运动矢量图,是解题的关键。
5.对多个用绳连接的物体系统,要牢记在绳的方向上各点的速度大小相等。
【例题5】如图所示,汽车沿水平路面以恒定速度v前进,则当拉绳与水平方向成θ角时,被吊起的物体M的速度为vM= 。 物体做什么样的运动?绳子拉力大小与物体重力大小的关系?
寻找分运动效果
θ
v
v
vA
vA=v sinθ
vA
θ
【例题5】如图所示,滑块沿杆匀速下滑,则当拉绳与水平方向成θ角时,被拉动的滑块的速度为vA= 。
【例题6】如图所示,A、B两物体用细绳相连,在水平面上运动,当α=450,β=300时,物体A的速度为2 m/s,这时B的速度为 。
寻找分运动效果
【答案】
2
运动的合成和分解
讨论
若人在河中始终保持头朝正前方游向对岸,你认为他会在对岸的正前方到达,还是会偏向上游或下游?为什么?
对于较复杂的运动,可以通过运动分解进行处理。达到简化模型的效果。
讨论
蜡块在平面内的运动:
问题1:蜡块同时参与了哪几个运动?蜡块实际运动是怎样的?这几个运动之间满足什么样的关系?
物体实际的运动叫合运动,物体同时参与合成的各个运动叫分运动。
合运动与分运动具有等效性
讨论
a
a1
a2
运动的合成与分解是指 x、v、 a 的合成与分解。
v1
v2
v
A
B
x
x1
x2
分速度
分速度
合速度
分加速度
合加速度
位移的合成
速度的合成
加速度的合成
分加速度
合位移
分位移
分位移
运动的合成是惟一的,而运动的分解不是惟一的,通常按运动所产生的实际效果分解。
讨论
蜡块在平面内的运动
问题2:合运动与分运动所用的时间有什么关系?
合运动与分运动具有等时性
讨论
蜡块在平面内的运动
问题3:若改变玻璃管水平方向运动的速度,蜡块从底部运动到端运动时间会变吗?水平速度变化会不会影响蜡块竖直方向的速度?这体现了分运动之间的什么特性?
分运动具有独立性
讨论
讨论
x
y
蜡块运动的轨迹:
x = vx t
y = vy t
消去时间t:
蜡块相对于黑板的运动轨迹是过原点的一条直线
理论分析:
讨论
x
y
理论分析:
蜡块的合位移:
位移的方向:
蜡块的合速度:
AC
讨论
物体实际的运动叫合运动,物体同时参与合成的各个运动叫分运动。由分运动求合运动的过程,叫做运动的合成;由合运动求分运动的过程,叫做运动的分解。运动的合成与分解遵从矢量运算法则(平行四边形定则)。
合运动与分运动的关系:
2.合运动与分运动具有等时性
3.分运动具有独立性
1.合运动与分运动具有等效性
讨论
如果红蜡块在竖直方向上的分运动是匀速直线运动,在水平方向上的分运动是匀加速直线运动,合运动的轨迹是什么样的?
如果两个方向上的分运动的都是匀加速直线运动,合运动的轨迹又是什么样的?
两个直线运动合成的合运动一定是直线运动吗?
讨论
蜡块在平面内的运动
问题4:蜡块实际运动是怎样的?你可以怎么处理这个复杂的运动?
问题5:如何将曲线运动进行分解?各分运动分别做什么样的运动?物体做曲线运动的原因是什么?
y
x
讨论
蜡块在平面内的运动
问题6:若已知竖直方向速度为Vy,水平方向加速度为a,能否算出物体的运动轨迹?
y
x
问题7:能否求出物体在t时刻的位移、速度及速度的方向?
讨论
1.关于运动的合成,下列说法中正确的是 ( )
A.合运动的速度一定比每一个分运动的速度大
B.两个速度不等的匀速直线运动的合运动,一 定是匀速直线运动
C.两个分运动是直线运动的合运动,一定是直线运动
D.两个分运动的时间,一定与它们的合运动的时间相等
讨论
2.降落伞在下落一定时间后的运动是匀速的。无风时某跳伞员竖直下落,着地时的速度是4m/s。现在有风,风可以使他以3m/s的速度沿水平方向向东运动,他将以多大的速度着地?
讨论
3、玻璃生产线上,宽9 m的成型玻璃板以2 m/s的速度连续不断地向前行进,在切割工序处,金刚钻的走刀速度为10 m/s,为了使割下的玻璃板都成规定尺寸的矩形,金刚钻割刀的轨道应如何控制 切割一次的时间多长
01
练习
02
思考
03
实践
课后作业
完成课后练习
感受电场的存在
电场的特点
分运动的位置,位移,速度,加速度
合运动的位置,位移,速度,加速度
运动的合成
运动的分解
遵循平行四边形定则
独立,等时,等效
力的作用效果相同
分力
合力
力的合成
平行四边形定则
以两个共点力为邻边作平行四边形,这两个邻边之间的对角线就表示合力的大小和方向
复习回顾
运动的作用效果相同
分运动
合运动
运动的合成
平行四边形定则
以两个共点运动为邻边作平行四边形,这两个邻边之间的对角线就表示合运动的大小和方向
知识推广
运动的合成与分解专题
【例题1】一船准备渡河,已知水流速度为v0=3m/s,船在静水中的航速为v’ =5m/s,河宽200m则:
①要使船能够垂直地渡过河去,那么应向何方划船?渡河时间是多少?
②要使船能在最短时间内渡河,应向何方划船?能否求出船到达河岸时的位置?
渡河问题
【例题2】宽300米,河水流速3m/s,船在静水中的航速为1m/s,则该船渡河的最短时间为 ,渡河的最短位移为 。
【答案】300 s, 900m
【例题3】有一小船正在渡河,如图所示,在离对岸30m时,其下游40m处有一危险水域,假若水流速度为5m/s,为了使小船在危险水域之前到达对岸,那么从现在起,小船相对于静水的最小速度应是多大?方向如何?
30m
40m
危险区
【例题4】如图所示,纤绳以恒定速率v沿水平方向通过定滑轮牵引小船靠岸,当纤绳与水面夹角为θ时,船靠岸的速度是 ,若使船匀速靠岸,则纤绳的速度是 。(填:匀速、加速、减速)
“绳+物”问题
①沿绳方向直线运动
②以定滑轮为圆心垂直绳的转动
寻找分运动效果
“绳+物”问题
【问题综述】 此类问题的关键是:
1.准确判断谁是合运动,谁是分运动;实际运动是合运动。
2.根据运动效果寻找分运动;
3.一般情况下,分运动表现在:
①沿绳方向的伸长或收缩运动;
②垂直于绳方向的旋转运动。
4.根据运动效果认真做好运动矢量图,是解题的关键。
5.对多个用绳连接的物体系统,要牢记在绳的方向上各点的速度大小相等。
【例题5】如图所示,汽车沿水平路面以恒定速度v前进,则当拉绳与水平方向成θ角时,被吊起的物体M的速度为vM= 。 物体做什么样的运动?绳子拉力大小与物体重力大小的关系?
寻找分运动效果
θ
v
v
vA
vA=v sinθ
vA
θ
【例题5】如图所示,滑块沿杆匀速下滑,则当拉绳与水平方向成θ角时,被拉动的滑块的速度为vA= 。
【例题6】如图所示,A、B两物体用细绳相连,在水平面上运动,当α=450,β=300时,物体A的速度为2 m/s,这时B的速度为 。
寻找分运动效果
【答案】
