必修 第一册 苏教版(新教材新标准) 章末复习提升(共18张PPT)
文档属性
| 名称 | 必修 第一册 苏教版(新教材新标准) 章末复习提升(共18张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 1.9MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏教版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-07-12 10:16:15 | ||
图片预览





文档简介
(共18张PPT)
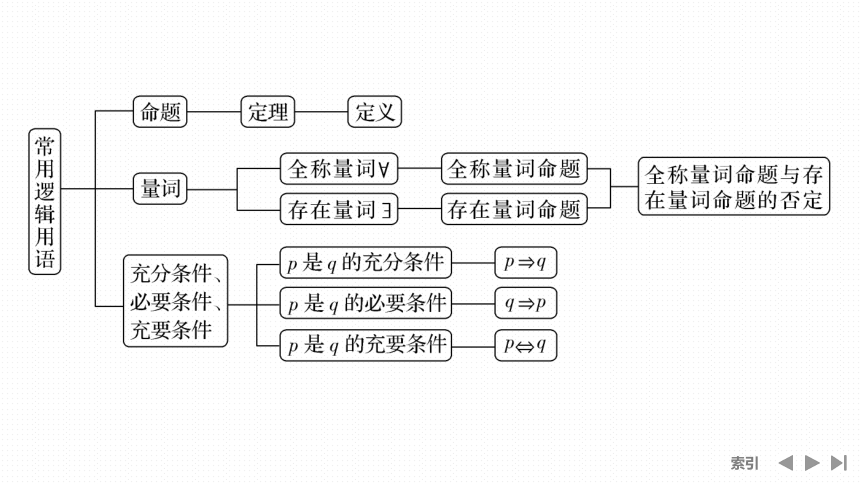
章末复习提升
网络构建
要点聚焦
内容索引
网络构建
形成体系
1
要点聚焦
类型突破
2
要点一 充分条件与必要条件
充分条件、必要条件、充要条件是数学的重要概念,在数学中有着非常广泛的应用,在高考中有着较高的考查频率,其特点是以高中数学的其它知识为载体考查充分条件、必要条件、充要条件的判断.
①若p q,则称p是q的充分条件,q是p的必要条件.
②若p q,则称p是q的充要条件.
【例1】 (1)已知集合A={x|-4≤x≤4,x∈R},B={x|x5”是“A B”的( )
A.充分条件但不是必要条件
B.必要条件但不是充分条件
C.充要条件
D.既不充分也不必要条件
A
(2)“不等式x2-2x+m≥0在R上恒成立”的一个充分条件但不是必要条件是( )
A.m≥1 B.m≤1
C.m≥0 D.m≥2
故“不等式x2-2x+m≥0在R上恒成立”的一个充分条件但不是必要条件是“m≥2”,故选D.
D
【训练1】 (1)若p:x2-x-12=0是q:ax-1=0的必要条件但不是充分条件,则实数a的值为________.
(2)若-a解析 (1)p:x2-x-12=0,即x=4或x=-3.
(2,+∞)
(2)根据充分条件、必要条件与集合间的包含关系,应有{x|-22.
要点二 全称量词命题与存在量词命题
1.书写命题的否定的方法:存在量词命题的否定是把存在量词改为全称量词的同时,对命题的结论进行否定;全称量词命题的否定是把全称量词改为存在量词的同时,对命题的结论进行否定.
简记:否量词(或改量词),否结论.
2.全称量词命题、存在量词命题的真假判断
(1)全称量词命题的真假判定:要判定一个全称量词命题为真,必须对限定集合M中每一个x,验证p(x)成立,一般用代数推理的方法加以证明;要判定一个全称量词命题为假,只需举出一个反例即可.
(2)存在量词命题的真假判定:要判定一个存在量词命题为真,只要在限定集合M中,找到一个x,使p(x)成立即可;否则,这一存在量词命题为假.
【例2】 (1)命题“ x∈R,x2-2x+1≥0”的否定是( )
A. x∈R,x2-2x+1≤0 B. x∈R,x2-2x+1≥0
C. x∈R,x2-2x+1<0 D. x∈R,x2-2x+1<0
(2)若命题p: x∈R,x2-2x+m≠0是真命题,则实数m的取值范围是( )
A.[1,+∞) B.(1,+∞) C.(-∞,1) D.(-∞,1]
解析 (1)∵命题“ x∈R,x2-2x+1≥0”为全称量词命题,
∴命题的否定为: x∈R,x2-2x+1<0,
故选C.
(2)命题p: x∈R,x2-2x+m≠0是真命题,则m≠-(x2-2x),∵-(x2-2x)=-(x-1)2+1≤1,∴m>1.
∴实数m的取值范围是(1,+∞).故选B.
C
B
【训练2】 (1)命题“ x∈R, n∈N*,使得n≥x2”的否定是( )
A. x∈R, n∈N*,使得nB. x∈R, n∈N*,使得nC. x∈R, n∈N*,使得nD. x∈R, n∈N*,使得n解析 含量词的命题的否定为改量词,否结论.
D
即(a-2)2<4,则-2即0D
要点三 转化与化归思想的应用
已知p与q的条件关系,可以转化为集合之间的包含关系;含量词命题的真假转化为相关知识.特别对有关参数取值范围问题,一定要辨清参数,恰当选取主元,合理确定解题思路.
【例3】 设p:实数x满足A={x|x≤3a或x≥a(a<0)},q:实数x满足B={x|-4≤x<-2},且q是p的充分条件但不是必要条件,求实数a的取值范围.
解 ∵q是p的充分条件但不是必要条件,
∴B?A,
【训练3】 (1)若“ x∈[-5,3],x2-2m+3>0”为真,求实数m的取值范围;
解 (1) x∈[-5,3],x2-2m+3>0可转化为x2>2m-3,
令y=x2,x∈[-5,3],∴ymin=0,∴0>2m-3,
本节内容结束
章末复习提升
网络构建
要点聚焦
内容索引
网络构建
形成体系
1
要点聚焦
类型突破
2
要点一 充分条件与必要条件
充分条件、必要条件、充要条件是数学的重要概念,在数学中有着非常广泛的应用,在高考中有着较高的考查频率,其特点是以高中数学的其它知识为载体考查充分条件、必要条件、充要条件的判断.
①若p q,则称p是q的充分条件,q是p的必要条件.
②若p q,则称p是q的充要条件.
【例1】 (1)已知集合A={x|-4≤x≤4,x∈R},B={x|x
A.充分条件但不是必要条件
B.必要条件但不是充分条件
C.充要条件
D.既不充分也不必要条件
A
(2)“不等式x2-2x+m≥0在R上恒成立”的一个充分条件但不是必要条件是( )
A.m≥1 B.m≤1
C.m≥0 D.m≥2
故“不等式x2-2x+m≥0在R上恒成立”的一个充分条件但不是必要条件是“m≥2”,故选D.
D
【训练1】 (1)若p:x2-x-12=0是q:ax-1=0的必要条件但不是充分条件,则实数a的值为________.
(2)若-a
(2,+∞)
(2)根据充分条件、必要条件与集合间的包含关系,应有{x|-2
要点二 全称量词命题与存在量词命题
1.书写命题的否定的方法:存在量词命题的否定是把存在量词改为全称量词的同时,对命题的结论进行否定;全称量词命题的否定是把全称量词改为存在量词的同时,对命题的结论进行否定.
简记:否量词(或改量词),否结论.
2.全称量词命题、存在量词命题的真假判断
(1)全称量词命题的真假判定:要判定一个全称量词命题为真,必须对限定集合M中每一个x,验证p(x)成立,一般用代数推理的方法加以证明;要判定一个全称量词命题为假,只需举出一个反例即可.
(2)存在量词命题的真假判定:要判定一个存在量词命题为真,只要在限定集合M中,找到一个x,使p(x)成立即可;否则,这一存在量词命题为假.
【例2】 (1)命题“ x∈R,x2-2x+1≥0”的否定是( )
A. x∈R,x2-2x+1≤0 B. x∈R,x2-2x+1≥0
C. x∈R,x2-2x+1<0 D. x∈R,x2-2x+1<0
(2)若命题p: x∈R,x2-2x+m≠0是真命题,则实数m的取值范围是( )
A.[1,+∞) B.(1,+∞) C.(-∞,1) D.(-∞,1]
解析 (1)∵命题“ x∈R,x2-2x+1≥0”为全称量词命题,
∴命题的否定为: x∈R,x2-2x+1<0,
故选C.
(2)命题p: x∈R,x2-2x+m≠0是真命题,则m≠-(x2-2x),∵-(x2-2x)=-(x-1)2+1≤1,∴m>1.
∴实数m的取值范围是(1,+∞).故选B.
C
B
【训练2】 (1)命题“ x∈R, n∈N*,使得n≥x2”的否定是( )
A. x∈R, n∈N*,使得n
D
即(a-2)2<4,则-2
要点三 转化与化归思想的应用
已知p与q的条件关系,可以转化为集合之间的包含关系;含量词命题的真假转化为相关知识.特别对有关参数取值范围问题,一定要辨清参数,恰当选取主元,合理确定解题思路.
【例3】 设p:实数x满足A={x|x≤3a或x≥a(a<0)},q:实数x满足B={x|-4≤x<-2},且q是p的充分条件但不是必要条件,求实数a的取值范围.
解 ∵q是p的充分条件但不是必要条件,
∴B?A,
【训练3】 (1)若“ x∈[-5,3],x2-2m+3>0”为真,求实数m的取值范围;
解 (1) x∈[-5,3],x2-2m+3>0可转化为x2>2m-3,
令y=x2,x∈[-5,3],∴ymin=0,∴0>2m-3,
本节内容结束
同课章节目录
- 第1章 集合
- 1.1 集合的概念与表示
- 1.2 子集、全集、补集
- 1.3 交集、并集
- 第2章 常用逻辑用语
- 2.1 命题、定理、定义
- 2.2 充分条件、必要条件、冲要条件
- 2.3 全称量词命题与存在量词命题
- 第3章 不等式
- 3.1 不等式的基本性质
- 3.2 基本不等式
- 3.3 从函数观点看一元二次方程和一元二次不等式
- 第4章 指数与对数
- 4.1 指数
- 4.2 对数
- 第5章 函数概念与性质
- 5.1 函数的概念和图象
- 5.2 函数的表示方法
- 5.3 函数的单调性
- 5.4 函数的奇偶性
- 第6章 幂函数、指数函数和对数函数
- 6.1 幂函数
- 6.2 指数函数
- 6.3 对数函数
- 第7章 三角函数
- 7.1 角与弧度
- 7.2 三角函数概念
- 7.3 三角函数的图象和性质
- 7.4 三角函数应用
- 第8章 函数应用
- 8.1 二分法与求方程近似解
- 8.2 函数与数学模型
