必修 第一册 苏教版(新教材新标准)3.3.3 一元二次不等式的应用(共49张PPT)
文档属性
| 名称 | 必修 第一册 苏教版(新教材新标准)3.3.3 一元二次不等式的应用(共49张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 4.0MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏教版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-07-12 10:13:25 | ||
图片预览











文档简介
(共49张PPT)
3.3.3 一元二次不等式的应用
1.借助二次函数的图象,了解一元二次不等式与相应函数、方程的联系.
2.能够从实际生活和生产中抽象出一元二次不等式的模型,并加以解决.
课标要求
素养要求
从函数观点认识不等式,解决不等式的实际问题,提升数学抽象素养、逻辑推理素养和数学运算素养,在解决实际问题时,培养数学建模素养.
课前预习
课堂互动
分层训练
内容索引
课前预习
知识探究
1
1.利用不等式解决实际问题的一般步骤如下:
(1)选取合适的字母表示题目中的未知数;
(2)由题目中给出的不等关系,列出关于未知数的不等式(组);
(3)求解所列出的不等式(组);
(4)结合题目的实际意义确定答案.
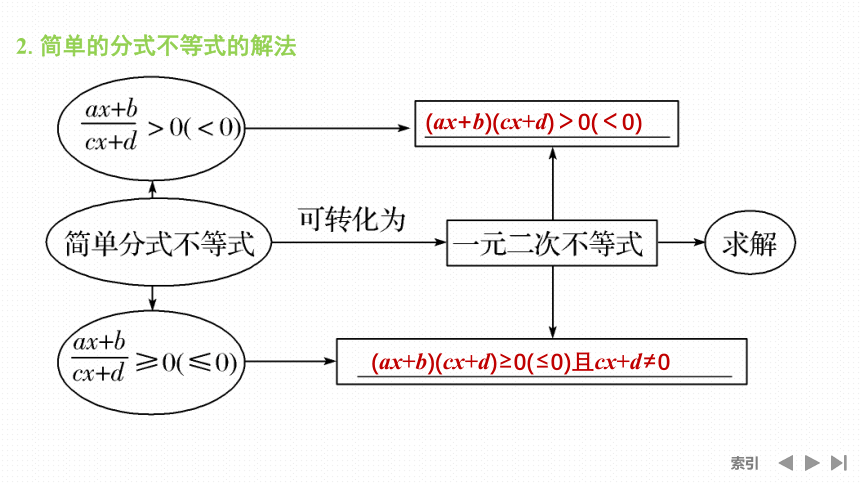
2.简单的分式不等式的解法
(ax+b)(cx+d)>0(<0)
(ax+b)(cx+d)≥0(≤0)且cx+d≠0
3.不等式恒成立问题
对于一元二次不等式恒成立问题,恒大于0就是相应的二次函数的图象在给定的区间上全部在x轴____方,恒小于0就是相应的二次函数的图象在给定的区间上全部在x轴____方.另外常转化为求二次函数的最值或用分离参数法求最值.
上
下
点睛
1.思考辨析,判断正误
(2)对于ax2+3x+2>0,当a=1时与a=-1时,对应的不等式解集不能求并集.( )
提示 两不等式等价,但函数图象不同.
√
提示 当a>0时成立,a<0时不等价.
(4)若不等式x2+mx+1≥0解集为R,则实数m的取值范围是[-2,2].( )
×
√
A.[1,2] B.(-∞,1]∪[2,+∞)
C.[1,2) D.(-∞,1]∪(2,+∞)
D
∴x>2或x≤1.
令y≥900,即60(8t-t2)≥900.解得3≤t≤5.
A.{t|1≤t≤3} B.{t|3≤t≤5}
C.{t|2≤t≤4} D.{t|4≤t≤6}
B
4.对任意的x∈R,函数y=x2+(a-4)x+(5-2a)的值恒大于0,则实数a的取值范围为_______________.
解析 要使y>0恒成立,只需Δ<0即可,
即(a-4)2-4(5-2a)<0,
解得-2{a|-2课堂互动
题型剖析
2
题型一 简单分式不等式的解法
【例1】 解不等式:
解 原不等式可化为(x+1)(2x-1)<0,
故原不等式的解集为{x|x<-2}.
思维升华
【训练1】 解下列不等式:
解 原不等式可化为
题型二 不等式在实际中的应用
【例2】 某农贸公司按每担200元的价格收购某农产品,并每100元纳税10元(又称征税率为10个百分点),计划可收购a万担.政府为了鼓励收购公司多收购这种农产品,决定将征税率降低x(x>0)个百分点,预测收购量可增加2x个百分点.
(1)写出降税后税收y(万元)与x的函数关系式;
解 降低税率后的税率为(10-x)%,农产品的收购量为a(1+2x%)万担,收购总金额为200a(1+2x%)万元.
依题意得y=200a(1+2x%)(10-x)%
化简得x2+40x-84≤0,
解得-42≤x≤2.
又因为0即x的取值范围为{x|0(2)要使此项税收在税率调节后,不少于原计划税收的83.2%,试确定x的取值范围.
解 原计划税收为200a·10%=20a(万元).
思维升华
解不等式应用题的步骤
【训练2】 某汽车厂上年度生产汽车的投入成本为10万元/辆,出厂价为12万元/辆,年销售量为10 000辆.本年度为适应市场需求,计划提高产品质量,适度增加投入成本.若每辆车投入成本增加的比例为x(0(1)写出本年度预计的年利润y与投入成本增加的比例x的关系式;
解 由题意得
y=[12(1+0.75x)-10(1+x)]×10 000×(1+0.6x)(0整理得y=-6 000x2+2 000x+20 000(0(2)为使本年度的年利润比上年度有所增加,则投入成本增加的比例x应在什么范围内?
解 要保证本年度的年利润比上年度有所增加,
题型三 不等式恒成立问题
角度1 在R上恒成立问题
【例3】 (1)已知不等式kx2+2kx-(k+2)<0恒成立,求实数k的取值范围;
解 当k=0时,原不等式化为-2<0,显然符合题意.
当k≠0时,令y=kx2+2kx-(k+2),∵y<0恒成立,
∴其图象都在x轴的下方,即开口向下,且与x轴无交点.
解得-1综上,实数k的取值范围是(-1,0].
(2)若不等式-x2+2x+3≤a2-3a对任意实数x恒成立,求实数a的取值范围.
解 原不等式可化为x2-2x+a2-3a-3≥0,
∵该不等式对任意实数x恒成立,∴Δ≤0,
即4-4(a2-3a-3)≤0,
即a2-3a-4≥0,
解得a≤-1或a≥4,
∴实数a的取值范围是(-∞,-1]∪[4,+∞).
角度2 在给定闭区间上的恒成立问题
【例4】 设函数y=mx2-mx-1.
(1)若对于一切实数x,y<0恒成立,求实数m的取值范围;
解 要使mx2-mx-1<0对x∈R恒成立,
若m=0,显然-1<0,满足题意;
∴-4即m的取值范围是(-4,0].
(2)对于x∈[1,3],y<-m+5恒成立,求实数m的取值范围.
解 当x∈[1,3]时,y<-m+5恒成立,
即当x∈[1,3]时,m(x2-x+1)-6<0恒成立.
又m(x2-x+1)-6<0,
思维升华
【训练3】 若不等式(m+1)x2-(m-1)x+3(m-1)<0对 x∈R恒成立,求实数m的取值范围.
解 由题意可知当m+1=0,即m=-1时,
原不等式可化为2x-6<0,解得x<3,不符合题意,应舍去.
当m+1≠0时,由(m+1)x2-(m-1)x+3(m-1)<0对 x∈R恒成立,
课堂小结
课堂小结
(3)利用不等式解决实际问题:
一般步骤
①选取合适字母表示未知数.
②由题目条件,列出关于未知数的不等式或不等式组.
③求解所列的不等式(组).
④结合题目的实际意义确定答案.
分层训练
素养提升
3
D
故-12.若集合A={x|ax2-ax+1<0}= ,则实数a的取值范围是( )
A.(0,4) B.[0,4) C.(0,4] D.[0,4]
解析 当a=0时,ax2-ax+1<0无解,符合题意;
当a<0时,ax2-ax+1<0的解集不可能为空集;
当a>0时,要使ax2-ax+1<0的解集为空集,
D
B
故选B.
D
4.对于任意实数x,不等式(a-2)x2-2(a-2)x-4<0恒成立,则实数a的取值范围为( )
A.{a|a<2} B.{a|a≤2}
C.{a|-2解析 当a-2=0,即a=2时,原不等式为-4<0,恒成立;
解得-2AB
5.(多选题)某小型服装厂生产一种风衣,日销售量x(件)与单价P(元)之间的关系为P=160-2x,生产x件所需成本为C(元),其中C=(500+30x)元.若要求每天获利不少于1 300元,则日销售量x的取值范围可以是( )
A.{x|20≤x≤30,x∈N*} B.{x|30≤x≤45,x∈N*}
C.{x|15≤x≤30,x∈N*} D.{x|15≤x≤45,x∈N*}
解析 设该厂每天获得的利润为y元,
则y=(160-2x)x-(500+30x)=-2x2+130x-500,0根据题意知,-2x2+130x-500≥1 300,解得20≤x≤45,
故当20≤x≤45且x∈N*时,每天获得的利润不少于1 300元.故选AB.
二、填空题
6.已知命题p: x∈R,ax2+ax+1>0为真命题,则实数a的取值范围是______________.
解析 当a=0时,1>0为真命题,符合题意;
当a≠0时,要使 x∈R,ax2+ax+1>0为真命题,
则对应的抛物线开口向上且与x轴没有交点,
[0,4)
综上可得,实数a的取值范围是[0,4).
7.将进货单价为80元的商品按90元一个售出时,能卖出400个,每涨价1元,其销售量就减少20个,为了使商家利润有所增加,售价b元所在的范围应是______________.
解析 设每个涨价a元,则涨价后的利润与原利润之差为(10+a)(400-20a)-10×400=-20a2+200a.
要使商家利润有所增加,则必须使-20a2+200a>0,即a2-10a<0,
得0∴售价b元所在的范围应为90{b|908.若关于x的不等式x2-ax-a≤-3的解集不是空集,则实数a的取值范围是_________________________.
解析 不等式x2-ax-a≤-3变形为x2-ax+3-a≤0,
∵不等式有解,
∴方程x2-ax+3-a=0的判别式Δ≥0,即a2-4(3-a)≥0,
解得a≤-6或a≥2,
故实数a的取值范围是(-∞,-6]∪[2,+∞).
(-∞,-6]∪[2,+∞)
10.已知不等式mx2-2x+m-2<0,若对于所有的实数x不等式恒成立,求实数m的取值范围.
解 对于所有实数x都有不等式mx2-2x+m-2<0恒成立,即函数y=mx2-2x+m-2的图象全部在x轴下方.
当m=0时,-2x-2<0,显然对任意x不能恒成立;
当m≠0时,由二次函数的图象可知有
B
11.若不等式x2-(a+1)x+a≤0的解集是[-4,3]的子集,则实数a的取值范围是( )
A.[-4,1] B.[-4,3] C.[1,3] D.[-1,3]
解析 由x2-(a+1)x+a≤0得(x-a)(x-1)≤0.
若a=1,则不等式的解集为{1},符合题意;
若a<1,则不等式的解集为[a,1],若满足[a,1] [-4,3],则-4≤a<1;
若a>1,则不等式的解集为[1,a],若满足[1,a] [-4,3],则1综上,-4≤a≤3,即实数a的取值范围是[-4,3].
12.某产品的总成本y(万元)与产量x(台)之间的函数关系是y=3 000+20x-0.1x2(0解析 依题意得25x≥3 000+20x-0.1x2,
整理得x2+50x-30 000≥0,
解得x≥150或x≤-200(舍去).
因为0即最低产量是150台.
150
13.已知不等式ax2+2ax+1≥0对任意x∈R恒成立,求关于x的不等式x2-x-a2+a<0的解集.
解 ∵ax2+2ax+1≥0对任意x∈R恒成立,
∴当a=0时,1≥0,不等式恒成立;
综上,0≤a≤1.
由x2-x-a2+a<0,得(x-a)[x-(1-a)]<0.
∵0≤a≤1,
B
14.若不等式x2+ax+1≥0对一切x∈(0,2]恒成立,则a的最小值是( )
解析 由于x∈(0,2],若不等式x2+ax+1≥0恒成立,
因此a≥-2,则a的最小值为-2.
本节内容结束
3.3.3 一元二次不等式的应用
1.借助二次函数的图象,了解一元二次不等式与相应函数、方程的联系.
2.能够从实际生活和生产中抽象出一元二次不等式的模型,并加以解决.
课标要求
素养要求
从函数观点认识不等式,解决不等式的实际问题,提升数学抽象素养、逻辑推理素养和数学运算素养,在解决实际问题时,培养数学建模素养.
课前预习
课堂互动
分层训练
内容索引
课前预习
知识探究
1
1.利用不等式解决实际问题的一般步骤如下:
(1)选取合适的字母表示题目中的未知数;
(2)由题目中给出的不等关系,列出关于未知数的不等式(组);
(3)求解所列出的不等式(组);
(4)结合题目的实际意义确定答案.
2.简单的分式不等式的解法
(ax+b)(cx+d)>0(<0)
(ax+b)(cx+d)≥0(≤0)且cx+d≠0
3.不等式恒成立问题
对于一元二次不等式恒成立问题,恒大于0就是相应的二次函数的图象在给定的区间上全部在x轴____方,恒小于0就是相应的二次函数的图象在给定的区间上全部在x轴____方.另外常转化为求二次函数的最值或用分离参数法求最值.
上
下
点睛
1.思考辨析,判断正误
(2)对于ax2+3x+2>0,当a=1时与a=-1时,对应的不等式解集不能求并集.( )
提示 两不等式等价,但函数图象不同.
√
提示 当a>0时成立,a<0时不等价.
(4)若不等式x2+mx+1≥0解集为R,则实数m的取值范围是[-2,2].( )
×
√
A.[1,2] B.(-∞,1]∪[2,+∞)
C.[1,2) D.(-∞,1]∪(2,+∞)
D
∴x>2或x≤1.
令y≥900,即60(8t-t2)≥900.解得3≤t≤5.
A.{t|1≤t≤3} B.{t|3≤t≤5}
C.{t|2≤t≤4} D.{t|4≤t≤6}
B
4.对任意的x∈R,函数y=x2+(a-4)x+(5-2a)的值恒大于0,则实数a的取值范围为_______________.
解析 要使y>0恒成立,只需Δ<0即可,
即(a-4)2-4(5-2a)<0,
解得-2
题型剖析
2
题型一 简单分式不等式的解法
【例1】 解不等式:
解 原不等式可化为(x+1)(2x-1)<0,
故原不等式的解集为{x|x<-2}.
思维升华
【训练1】 解下列不等式:
解 原不等式可化为
题型二 不等式在实际中的应用
【例2】 某农贸公司按每担200元的价格收购某农产品,并每100元纳税10元(又称征税率为10个百分点),计划可收购a万担.政府为了鼓励收购公司多收购这种农产品,决定将征税率降低x(x>0)个百分点,预测收购量可增加2x个百分点.
(1)写出降税后税收y(万元)与x的函数关系式;
解 降低税率后的税率为(10-x)%,农产品的收购量为a(1+2x%)万担,收购总金额为200a(1+2x%)万元.
依题意得y=200a(1+2x%)(10-x)%
化简得x2+40x-84≤0,
解得-42≤x≤2.
又因为0
解 原计划税收为200a·10%=20a(万元).
思维升华
解不等式应用题的步骤
【训练2】 某汽车厂上年度生产汽车的投入成本为10万元/辆,出厂价为12万元/辆,年销售量为10 000辆.本年度为适应市场需求,计划提高产品质量,适度增加投入成本.若每辆车投入成本增加的比例为x(0
解 由题意得
y=[12(1+0.75x)-10(1+x)]×10 000×(1+0.6x)(0
解 要保证本年度的年利润比上年度有所增加,
题型三 不等式恒成立问题
角度1 在R上恒成立问题
【例3】 (1)已知不等式kx2+2kx-(k+2)<0恒成立,求实数k的取值范围;
解 当k=0时,原不等式化为-2<0,显然符合题意.
当k≠0时,令y=kx2+2kx-(k+2),∵y<0恒成立,
∴其图象都在x轴的下方,即开口向下,且与x轴无交点.
解得-1
(2)若不等式-x2+2x+3≤a2-3a对任意实数x恒成立,求实数a的取值范围.
解 原不等式可化为x2-2x+a2-3a-3≥0,
∵该不等式对任意实数x恒成立,∴Δ≤0,
即4-4(a2-3a-3)≤0,
即a2-3a-4≥0,
解得a≤-1或a≥4,
∴实数a的取值范围是(-∞,-1]∪[4,+∞).
角度2 在给定闭区间上的恒成立问题
【例4】 设函数y=mx2-mx-1.
(1)若对于一切实数x,y<0恒成立,求实数m的取值范围;
解 要使mx2-mx-1<0对x∈R恒成立,
若m=0,显然-1<0,满足题意;
∴-4
(2)对于x∈[1,3],y<-m+5恒成立,求实数m的取值范围.
解 当x∈[1,3]时,y<-m+5恒成立,
即当x∈[1,3]时,m(x2-x+1)-6<0恒成立.
又m(x2-x+1)-6<0,
思维升华
【训练3】 若不等式(m+1)x2-(m-1)x+3(m-1)<0对 x∈R恒成立,求实数m的取值范围.
解 由题意可知当m+1=0,即m=-1时,
原不等式可化为2x-6<0,解得x<3,不符合题意,应舍去.
当m+1≠0时,由(m+1)x2-(m-1)x+3(m-1)<0对 x∈R恒成立,
课堂小结
课堂小结
(3)利用不等式解决实际问题:
一般步骤
①选取合适字母表示未知数.
②由题目条件,列出关于未知数的不等式或不等式组.
③求解所列的不等式(组).
④结合题目的实际意义确定答案.
分层训练
素养提升
3
D
故-1
A.(0,4) B.[0,4) C.(0,4] D.[0,4]
解析 当a=0时,ax2-ax+1<0无解,符合题意;
当a<0时,ax2-ax+1<0的解集不可能为空集;
当a>0时,要使ax2-ax+1<0的解集为空集,
D
B
故选B.
D
4.对于任意实数x,不等式(a-2)x2-2(a-2)x-4<0恒成立,则实数a的取值范围为( )
A.{a|a<2} B.{a|a≤2}
C.{a|-2
解得-2
5.(多选题)某小型服装厂生产一种风衣,日销售量x(件)与单价P(元)之间的关系为P=160-2x,生产x件所需成本为C(元),其中C=(500+30x)元.若要求每天获利不少于1 300元,则日销售量x的取值范围可以是( )
A.{x|20≤x≤30,x∈N*} B.{x|30≤x≤45,x∈N*}
C.{x|15≤x≤30,x∈N*} D.{x|15≤x≤45,x∈N*}
解析 设该厂每天获得的利润为y元,
则y=(160-2x)x-(500+30x)=-2x2+130x-500,0
故当20≤x≤45且x∈N*时,每天获得的利润不少于1 300元.故选AB.
二、填空题
6.已知命题p: x∈R,ax2+ax+1>0为真命题,则实数a的取值范围是______________.
解析 当a=0时,1>0为真命题,符合题意;
当a≠0时,要使 x∈R,ax2+ax+1>0为真命题,
则对应的抛物线开口向上且与x轴没有交点,
[0,4)
综上可得,实数a的取值范围是[0,4).
7.将进货单价为80元的商品按90元一个售出时,能卖出400个,每涨价1元,其销售量就减少20个,为了使商家利润有所增加,售价b元所在的范围应是______________.
解析 设每个涨价a元,则涨价后的利润与原利润之差为(10+a)(400-20a)-10×400=-20a2+200a.
要使商家利润有所增加,则必须使-20a2+200a>0,即a2-10a<0,
得0
解析 不等式x2-ax-a≤-3变形为x2-ax+3-a≤0,
∵不等式有解,
∴方程x2-ax+3-a=0的判别式Δ≥0,即a2-4(3-a)≥0,
解得a≤-6或a≥2,
故实数a的取值范围是(-∞,-6]∪[2,+∞).
(-∞,-6]∪[2,+∞)
10.已知不等式mx2-2x+m-2<0,若对于所有的实数x不等式恒成立,求实数m的取值范围.
解 对于所有实数x都有不等式mx2-2x+m-2<0恒成立,即函数y=mx2-2x+m-2的图象全部在x轴下方.
当m=0时,-2x-2<0,显然对任意x不能恒成立;
当m≠0时,由二次函数的图象可知有
B
11.若不等式x2-(a+1)x+a≤0的解集是[-4,3]的子集,则实数a的取值范围是( )
A.[-4,1] B.[-4,3] C.[1,3] D.[-1,3]
解析 由x2-(a+1)x+a≤0得(x-a)(x-1)≤0.
若a=1,则不等式的解集为{1},符合题意;
若a<1,则不等式的解集为[a,1],若满足[a,1] [-4,3],则-4≤a<1;
若a>1,则不等式的解集为[1,a],若满足[1,a] [-4,3],则1
12.某产品的总成本y(万元)与产量x(台)之间的函数关系是y=3 000+20x-0.1x2(0
整理得x2+50x-30 000≥0,
解得x≥150或x≤-200(舍去).
因为0
150
13.已知不等式ax2+2ax+1≥0对任意x∈R恒成立,求关于x的不等式x2-x-a2+a<0的解集.
解 ∵ax2+2ax+1≥0对任意x∈R恒成立,
∴当a=0时,1≥0,不等式恒成立;
综上,0≤a≤1.
由x2-x-a2+a<0,得(x-a)[x-(1-a)]<0.
∵0≤a≤1,
B
14.若不等式x2+ax+1≥0对一切x∈(0,2]恒成立,则a的最小值是( )
解析 由于x∈(0,2],若不等式x2+ax+1≥0恒成立,
因此a≥-2,则a的最小值为-2.
本节内容结束
同课章节目录
- 第1章 集合
- 1.1 集合的概念与表示
- 1.2 子集、全集、补集
- 1.3 交集、并集
- 第2章 常用逻辑用语
- 2.1 命题、定理、定义
- 2.2 充分条件、必要条件、冲要条件
- 2.3 全称量词命题与存在量词命题
- 第3章 不等式
- 3.1 不等式的基本性质
- 3.2 基本不等式
- 3.3 从函数观点看一元二次方程和一元二次不等式
- 第4章 指数与对数
- 4.1 指数
- 4.2 对数
- 第5章 函数概念与性质
- 5.1 函数的概念和图象
- 5.2 函数的表示方法
- 5.3 函数的单调性
- 5.4 函数的奇偶性
- 第6章 幂函数、指数函数和对数函数
- 6.1 幂函数
- 6.2 指数函数
- 6.3 对数函数
- 第7章 三角函数
- 7.1 角与弧度
- 7.2 三角函数概念
- 7.3 三角函数的图象和性质
- 7.4 三角函数应用
- 第8章 函数应用
- 8.1 二分法与求方程近似解
- 8.2 函数与数学模型
