必修 第一册 苏教版(新教材新标准)第三章不等式 章末复习提升(共26张PPT)
文档属性
| 名称 | 必修 第一册 苏教版(新教材新标准)第三章不等式 章末复习提升(共26张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 3.1MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏教版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-07-12 10:19:03 | ||
图片预览







文档简介
(共26张PPT)
章末复习提升
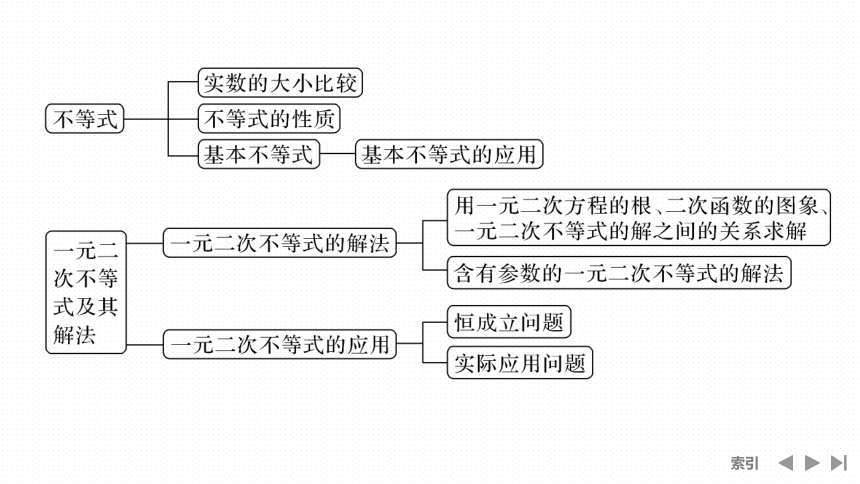
网络构建
要点聚焦
内容索引
网络构建
形成体系
1
要点聚焦
类型突破
2
要点一 不等式的性质
不等式的性质常用来比较大小和证明不等式,防止由于考虑不全面出现错误,有时也可结合特殊值法求解.
【例1】 (1)如果a,b,c满足cA.ab>ac B.c(b-a)>0
C.cb2解析 因为c0.
A成立,因为cac.
B成立,因为b0.
C不一定成立,当b=0时,cb2D成立,因为c0,所以ac(a-c)<0.
C
解 因为-2又因为2因为-2【训练1】 (1)下列结论正确的是( )
A.若aB.若a2>b2,则a>b
C.若a>b,c<0,则a+c解析 A中,当c=0时不符,所以A错误;
B中,当a=-2,b=-1时,符合a2>b2,不满足a>b,B错误;
C中,a+c>b+c,所以C错误;
D
(2)已知x>y>z,x+y+z=0,则下列不等式中一定成立的是( )
A.xy>yz B.xz>yz
C.xy>xz D.x|y|>z|y|
解析 因为x>y>z,x+y+z=0,
所以3x>x+y+z=0,3z所以x>0,z<0.
C
要点二 基本不等式的应用
运用基本不等式求最值时把握三个条件
(1)“一正”——各项为正数;
(2)“二定”——“和”或“积”为定值;
(3)“三相等”——等号一定能取到.这三个条件缺一不可.
利用基本不等式求最值,通过恒等变形及配凑,使“和”或“积”为定值,常用变形技巧如下:
(1)拆——裂项拆项
对分子的次数不低于分母次数的分式进行整式分离——分离成整式与“真分式”的和,再根据分式中分母的情况对整式进行拆项,为应用基本不等式凑定积创造条件.
(2)并——分组并项
目的是分组后各组可以单独应用基本不等式,或分组后先对一组应用基本不等式,再在组与组之间应用基本不等式得出最值.
(3)配——配式、配系数
有时为了挖掘出“积”或“和”为定值,常常需要根据题设条件采取合理配式、配系数的方法,使配式与待求式相乘后可以应用基本不等式得出定值,或配以恰当的系数后,使积式中的各项之和为定值.
【训练2】 (1)已知x>0,y>0,x+2y+2xy=8,则x+2y的最小值为( )
A.2 B.4 C.6 D.8
解析 法一 依题意得x+1>1,2y+1>1,
B
由x+2y+2xy=8,得(x+1)(2y+1)=9,
当且仅当x+1=2y+1=3,即x=2,y=1时,等号成立,
因此有x+2y≥4,所以x+2y的最小值为4.
所以x+2y的最小值为4.
又∵a是正数,b也是正数,
要点三 一元二次不等式的解法
1.解一元二次不等式(分式不等式)首先转化为标准形式(二次项系数为正),然后能分解因式的变成因式相乘的形式,从而得到不等式的解集.
2.对于含参数的不等式要注意对参数进行讨论,做到不重不漏.
【例3】 解关于x的不等式ax2-2(a+1)x+4>0.
解 (1)当a=0时,原不等式可化为-2x+4>0,
解得x<2,所以原不等式的解集为{x|x<2}.
(2)当a>0时,原不等式可化为(ax-2)(x-2)>0,
a=0时,原不等式的解集为{x|x<2};
解 将a=-2代入不等式,
解得-2要点四 恒成立问题
对于不等式恒成立求参数范围问题常见类型及解法有以下几种
(1)变更主元法:
根据实际情况的需要确定合适的主元,一般知道取值范围的变量要看作主元.
(2)分离参数法:
将参数分离转化为求解最值问题.
(3)数形结合法:
利用不等式与函数的关系将恒成立问题通过函数图象直观化.
【例4】 求使不等式x2+(a-6)x+9-3a>0,-1≤a≤1恒成立的x的取值范围.
解 将原不等式整理为形式上是关于a的不等式(x-3)a+x2-6x+9>0.
设关于a的一次函数为y=(x-3)a+x2-6x+9.
因为y>0,当-1≤a≤1时恒成立,所以
(1)若x=3,则y=0,不符合题意,应舍去.
(2)若x≠3,则由一次函数的图象,
解得x<2或x>4.
所以x的取值范围是{x|x<2或x>4}.
等价于x2+2x+a>0恒成立,
即a>-(x2+2x)恒成立,
故a>[-(x2+2x)]max.
令y1=-(x2+2x),则
当x≥1时,y1=-(x2+2x)=-(x2+2x+1)+1
=-(x+1)2+1≤-3.
∴实数a的取值范围为{a|a>-3}.
本节内容结束
章末复习提升
网络构建
要点聚焦
内容索引
网络构建
形成体系
1
要点聚焦
类型突破
2
要点一 不等式的性质
不等式的性质常用来比较大小和证明不等式,防止由于考虑不全面出现错误,有时也可结合特殊值法求解.
【例1】 (1)如果a,b,c满足c
C.cb2
A成立,因为c
B成立,因为b
C不一定成立,当b=0时,cb2
C
解 因为-2
A.若a
C.若a>b,c<0,则a+c
B中,当a=-2,b=-1时,符合a2>b2,不满足a>b,B错误;
C中,a+c>b+c,所以C错误;
D
(2)已知x>y>z,x+y+z=0,则下列不等式中一定成立的是( )
A.xy>yz B.xz>yz
C.xy>xz D.x|y|>z|y|
解析 因为x>y>z,x+y+z=0,
所以3x>x+y+z=0,3z
C
要点二 基本不等式的应用
运用基本不等式求最值时把握三个条件
(1)“一正”——各项为正数;
(2)“二定”——“和”或“积”为定值;
(3)“三相等”——等号一定能取到.这三个条件缺一不可.
利用基本不等式求最值,通过恒等变形及配凑,使“和”或“积”为定值,常用变形技巧如下:
(1)拆——裂项拆项
对分子的次数不低于分母次数的分式进行整式分离——分离成整式与“真分式”的和,再根据分式中分母的情况对整式进行拆项,为应用基本不等式凑定积创造条件.
(2)并——分组并项
目的是分组后各组可以单独应用基本不等式,或分组后先对一组应用基本不等式,再在组与组之间应用基本不等式得出最值.
(3)配——配式、配系数
有时为了挖掘出“积”或“和”为定值,常常需要根据题设条件采取合理配式、配系数的方法,使配式与待求式相乘后可以应用基本不等式得出定值,或配以恰当的系数后,使积式中的各项之和为定值.
【训练2】 (1)已知x>0,y>0,x+2y+2xy=8,则x+2y的最小值为( )
A.2 B.4 C.6 D.8
解析 法一 依题意得x+1>1,2y+1>1,
B
由x+2y+2xy=8,得(x+1)(2y+1)=9,
当且仅当x+1=2y+1=3,即x=2,y=1时,等号成立,
因此有x+2y≥4,所以x+2y的最小值为4.
所以x+2y的最小值为4.
又∵a是正数,b也是正数,
要点三 一元二次不等式的解法
1.解一元二次不等式(分式不等式)首先转化为标准形式(二次项系数为正),然后能分解因式的变成因式相乘的形式,从而得到不等式的解集.
2.对于含参数的不等式要注意对参数进行讨论,做到不重不漏.
【例3】 解关于x的不等式ax2-2(a+1)x+4>0.
解 (1)当a=0时,原不等式可化为-2x+4>0,
解得x<2,所以原不等式的解集为{x|x<2}.
(2)当a>0时,原不等式可化为(ax-2)(x-2)>0,
a=0时,原不等式的解集为{x|x<2};
解 将a=-2代入不等式,
解得-2
对于不等式恒成立求参数范围问题常见类型及解法有以下几种
(1)变更主元法:
根据实际情况的需要确定合适的主元,一般知道取值范围的变量要看作主元.
(2)分离参数法:
将参数分离转化为求解最值问题.
(3)数形结合法:
利用不等式与函数的关系将恒成立问题通过函数图象直观化.
【例4】 求使不等式x2+(a-6)x+9-3a>0,-1≤a≤1恒成立的x的取值范围.
解 将原不等式整理为形式上是关于a的不等式(x-3)a+x2-6x+9>0.
设关于a的一次函数为y=(x-3)a+x2-6x+9.
因为y>0,当-1≤a≤1时恒成立,所以
(1)若x=3,则y=0,不符合题意,应舍去.
(2)若x≠3,则由一次函数的图象,
解得x<2或x>4.
所以x的取值范围是{x|x<2或x>4}.
等价于x2+2x+a>0恒成立,
即a>-(x2+2x)恒成立,
故a>[-(x2+2x)]max.
令y1=-(x2+2x),则
当x≥1时,y1=-(x2+2x)=-(x2+2x+1)+1
=-(x+1)2+1≤-3.
∴实数a的取值范围为{a|a>-3}.
本节内容结束
同课章节目录
- 第1章 集合
- 1.1 集合的概念与表示
- 1.2 子集、全集、补集
- 1.3 交集、并集
- 第2章 常用逻辑用语
- 2.1 命题、定理、定义
- 2.2 充分条件、必要条件、冲要条件
- 2.3 全称量词命题与存在量词命题
- 第3章 不等式
- 3.1 不等式的基本性质
- 3.2 基本不等式
- 3.3 从函数观点看一元二次方程和一元二次不等式
- 第4章 指数与对数
- 4.1 指数
- 4.2 对数
- 第5章 函数概念与性质
- 5.1 函数的概念和图象
- 5.2 函数的表示方法
- 5.3 函数的单调性
- 5.4 函数的奇偶性
- 第6章 幂函数、指数函数和对数函数
- 6.1 幂函数
- 6.2 指数函数
- 6.3 对数函数
- 第7章 三角函数
- 7.1 角与弧度
- 7.2 三角函数概念
- 7.3 三角函数的图象和性质
- 7.4 三角函数应用
- 第8章 函数应用
- 8.1 二分法与求方程近似解
- 8.2 函数与数学模型
