北师大版数学 八年级上册 第四章 一次函数 单元测试(word版 含解析)
文档属性
| 名称 | 北师大版数学 八年级上册 第四章 一次函数 单元测试(word版 含解析) |

|
|
| 格式 | docx | ||
| 文件大小 | 173.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-07-11 00:00:00 | ||
图片预览

文档简介
第四章 一次函数
一 选择题(共10小题,每小题3分,共30分.每小题有四个选项,其中只有一个选项符合题意)
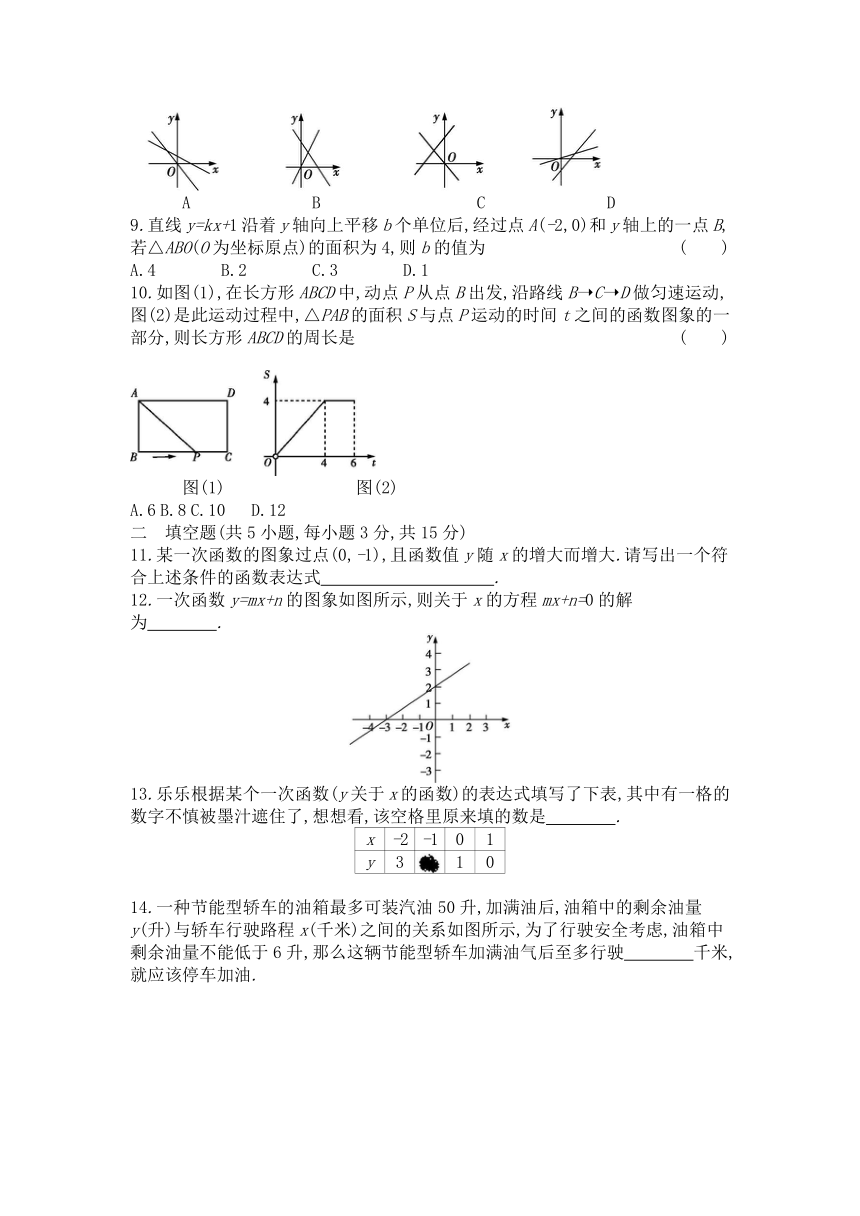
1.下列平面直角坐标系中的图象,不能表示y是x的函数的是 ( )
A B C D
2.有下列函数:①y=3πx;②y=8x-6;③y=;④y=-8x;⑤y=5x2-4x+1.其中是一次函数的有 ( )
A.4个 B.3个 C.2个 D.1个
3.对于函数y=-3x+1,下列结论正确的是 ( )
A.y随x的增大而增大
B.它的图象经过第一、二、三象限
C.它的图象必经过点(0,1)
D.当x=1时,y=2
4.用长为50的栏杆围成一个长为x宽为y的长方形,则y与x之间的函数关系为 ( )
A.y=25-x B.y=25+x C.y=50-x D.y=50+x
5.小明从家到学校,先匀速步行到公交车站,等了几分钟后坐上了公交车,公交车沿着公路匀速行驶一段时间后到达学校,则小明从家到学校的路程s与时间t之间的图象大致是 ( )
A B C D
6.在平面直角坐标系中,点A(2,m)关于y对称的点B在直线y=-x+1上,则m的值为 ( )
A.1 B.3 C.-3 D.2
7.如图,三个一次函数y=ax,y=bx,y=cx-3的图象如图所示,则a,b,c的大小关系是 ( )
A.b>a>c B.c>b>a
C.a>b>c D.c>a>b
8.下列图形中,能表示一次函数y=mx+n与正比例函数y=mnx(m,n为常数,且mn≠0)的图象的是 ( )
A B C D
9.直线y=kx+1沿着y轴向上平移b个单位后,经过点A(-2,0)和y轴上的一点B,若△ABO(O为坐标原点)的面积为4,则b的值为 ( )
A.4 B.2 C.3 D.1
10.如图(1),在长方形ABCD中,动点P从点B出发,沿路线B C D做匀速运动,图(2)是此运动过程中,△PAB的面积S与点P运动的时间t之间的函数图象的一部分,则长方形ABCD的周长是 ( )
图(1) 图(2)
A.6 B.8 C.10 D.12
二 填空题(共5小题,每小题3分,共15分)
11.某一次函数的图象过点(0,-1),且函数值y随x的增大而增大.请写出一个符合上述条件的函数表达式 .
12.一次函数y=mx+n的图象如图所示,则关于x的方程mx+n=0的解为 .
13.乐乐根据某个一次函数(y关于x的函数)的表达式填写了下表,其中有一格的数字不慎被墨汁遮住了,想想看,该空格里原来填的数是 .
x -2 -1 0 1
y 3 1 0
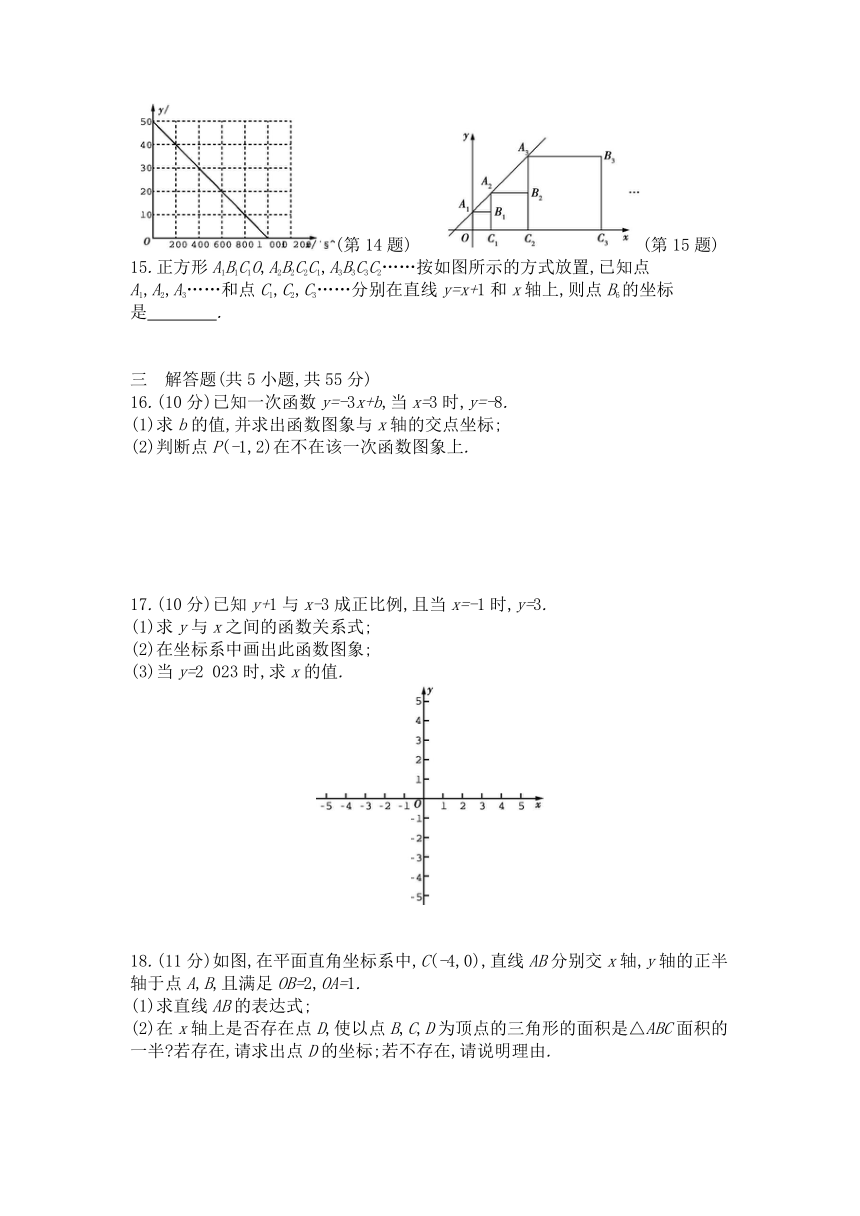
14.一种节能型轿车的油箱最多可装汽油50升,加满油后,油箱中的剩余油量y(升)与轿车行驶路程x(千米)之间的关系如图所示,为了行驶安全考虑,油箱中剩余油量不能低于6升,那么这辆节能型轿车加满油气后至多行驶 千米,就应该停车加油.
(第14题) (第15题)
15.正方形A1B1C1O,A2B2C2C1,A3B3C3C2……按如图所示的方式放置,已知点A1,A2,A3……和点C1,C2,C3……分别在直线y=x+1和x轴上,则点B6的坐标是 .
三 解答题(共5小题,共55分)
16.(10分)已知一次函数y=-3x+b,当x=3时,y=-8.
(1)求b的值,并求出函数图象与x轴的交点坐标;
(2)判断点P(-1,2)在不在该一次函数图象上.
17.(10分)已知y+1与x-3成正比例,且当x=-1时,y=3.
(1)求y与x之间的函数关系式;
(2)在坐标系中画出此函数图象;
(3)当y=2 023时,求x的值.
18.(11分)如图,在平面直角坐标系中,C(-4,0),直线AB分别交x轴,y轴的正半轴于点A,B,且满足OB=2,OA=1.
(1)求直线AB的表达式;
(2)在x轴上是否存在点D,使以点B,C,D为顶点的三角形的面积是△ABC面积的一半 若存在,请求出点D的坐标;若不存在,请说明理由.
19.(12分)甲、乙两个商场出售相同的某种商品,每件定价均为3 000元,并且多买都有一定的优惠.甲商场的优惠条件是:第一件按定价收费,其余每件优惠30%.乙商场的优惠条件是:每件优惠25%.设所买商品为x件时,甲商场收费为y1元,乙商场收费为y2元.
(1)分别求出y1,y2与x之间的函数关系式;
(2)当甲、乙两个商场的收费相同时,所买商品为多少件
(3)当所买商品为5件时,选择哪个商场更优惠 请说明理由.
20.(12分)如图,甲、乙两车分别从两地同时出发,且沿同一路线同向行驶,l1和l2分别表示甲、乙两车行驶的路程与时间的函数图象,请结合图象,解决下列问题:
(1)在刚出发时,甲车距乙车多少千米
(2)甲车与乙车的速度分别是多少
(3)分别求出l1,l2的函数表达式.
(4)当甲车与乙车相距100 km时,它们出发了多久
1.D 若y是x的函数,则对于自变量x的每一个值,因变量y都有唯一的值与它对应,故选D.
2.B y=3πx,y=8x-6,y=-8x是一次函数.y=的自变量的次数不为1,而为-1,不是一次函数.y=5x2-4x+1的自变量的最高次数不为1,而为2,不是一次函数.故选B.
3.C ∵一次函数y=-3x+1中的k=-3<0,b=1>0,∴y随x的增大而减小,且图象经过第一、二、四象限;∵当x=0时,y=1,∴它的图象必经过点(0,1);当x=1时,y=-2.故选C.
4.A 由题意得x+y=25,∴y=25-x.故选A.
5.B 小明从家匀速步行到公交车站,s的值随时间t的增大而增大,等了几分钟后坐上了公交车,在等车这个过程中,s的值不随时间t发生变化,公交车沿着公路匀速行驶一段时间后到达学校,s的值随时间t的增大而增大的较快,故选B.
6.B ∵点A(2,m)与点B关于y轴对称, ∴B(-2,m).∵点B在y=-x+1上,∴ m=-(-2)+1=3.故选B.
7.A 由题图可得a>0,b>0,c<0,且aa>c.故选A.
8.A ①当mn>0时,m,n同号,y=mnx的图象过第一、三象限,m,n同为正号时y=mx+n过第一、二、三象限;m,n同为负号时y=mx+n过第二、三、四象限.②当mn<0时,m,n异号,y=mnx的图象过第二、四象限,m>0,n<0时,y=mx+n过第一、三、四象限;m<0,n>0时,y=mx+n过第一、二、四象限.故选A.
9.C 直线y=kx+1沿着y轴向上平移b个单位后,得到y=kx+b+1,∴B(0,b+1),∴×2×(b+1)=4,解得b=3.故选C.
10.D 因为当点P到达点C时,△PAB的面积最大,此时△PAB的面积=×AB×BC=4.设动点P的速度为v,由题图(2)可得CD=AB=2v,BC=4v, 即×2v×4v=4,因为v>0所以v=1,所以AB=2,BC=4,所以长方形ABCD的周长=(2+4)×2=12.故选D.
11.y=x-1(y=kx-1,k>0即可) 【解析】由题意设y=kx-1,由函数值y随x的增大而增大,得到k>0,则满足上述条件的函数表达式可以为y=x-1.
12.x=-3 【解析】∵一次函数y=mx+n的图象与x轴的交点为(-3,0),∴当mx+n=0时,x=-3.
13.2 【解析】设一次函数的表达式为y=kx+b(k≠0),由该函数的图象经过点(0,1),(1,0),可得b=1,k=-1,所以该函数的表达式为y=-x+1.当x=-1时,y=2.
14.880 【解析】设y与x之间的关系式为y=kx+b(k≠0),将(0,50),(1 000,0)代入,得解得故y与x之间的关系式为y=-0.05x+50(0≤x≤1 000).把y=6代入,得6=-0.05x+50,解得x=880.
15.(63,32) 【解析】∵OC1=OA1=B1C1=A1B1=1,∴B1(1,1).∵点A2在直线y=x+1上,∴A2(1,2),∴B2C2=C1A2=C1C2=2,∴B2(3,2),同理可得B3(7,4),B4(15,8),B5(31,16),B6(63,32),∴点B6的坐标为(63,32).
16.【解题思路】(1)把已知值代入表达式可得关于b的方程,通过解方程,求得b的值.令y=0,求得x的值,可得函数图象与x轴的交点坐标.(2)把点P(-1,2)的坐标代入表达式,进行判断.
【参考答案】(1)把x=3,y=-8代入y=-3x+b,
得-3×3+b=-8,
∴b=1,
∴y=-3x+1. (3分)
令y=0,得-3x+1=0,
∴x=,
∴函数图象与x轴的交点坐标为(,0). (6分)
(2)把x=-1代入y=-3x+1,得y=4≠2,
∴点P不在该一次函数图象上. (10分)
17.【参考答案】(1)∵ y+1与x-3成正比例,
∴设y+1=k(x-3),
把x=-1,y=3代入,得4=-4k,
∴k=-1,
∴y与x之间的函数关系式为y+1=-(x-3), 即y=-x+2. (4分)
(2)令x=0, 则y=2,
令y=0, 则x=2,
如图,描点(0,2),(2,0), 连线即可. (8分)
(3)由题意得2 023=-x+2,解得x=-2 021. (10分)
18.【参考答案】(1)∵OB=2,OA=1,
∴点A的坐标为(1,0),点B的坐标为(0,2),
设直线AB的表达式为y=kx+2,
将点A的坐标代入,得0=k+2,
解得k=-2,
∴直线AB的表达式为y=-2x+2. (4分)
(2)存在.
设点D的坐标为(x,0),
∵A(1,0),B(0,2),C(-4,0),
∴AC=5,
∴S△ABC=×5×2=5.
∵S△BCD=S△ABC,
∴S△BCD=CD·OB=,
即|x-(-4)|×2=,
∴|x+4|=,
∴x=-或x=-,
∴点D的坐标为(-,0)或(-,0). (11分)
19.【解题思路】(1)根据两个商场的优惠条件列出函数关系式;(2)求收费相同时所买商品的件数,也就是求y1=y2时x的值;(3)当x=5时分别求出y1,y2的值,再进行比较即可.
【参考答案】(1)由题意,得y1=3 000×(1-30%)(x-1)+3 000=2 100x+900; (2分)
y2=3 000×(1-25%)x=2 250x. (4分)
(2)当y1=y2时,即2 100x+900=2 250x,解得x=6.
所以当甲、乙两个商场的收费相同时,所买商品为6件. (8分)
(3)选择乙商场更优惠.理由如下:
当x=5时,y1=2 100×5+900=11 400,
y2=2 250×5=11 250.
因为11 250<11 400,
所以当所买商品为5件时,选择乙商场更优惠. (12分)
20.【参考答案】(1)因为l1与y轴的交点为(0,500),l2与y轴的交点为(0,0),500-0=500(km),
所以在刚出发时,甲车距乙车500 km. (2分)
(2)(900-500)÷4=100(km/h),600÷4=150(km/h),所以甲车的速度是100 km/h,乙车的速度是150 km/h. (4分)
(3)设l1的函数表达式为y1=kt+b(k≠0),
将(0,500),(4,900)代入y1=kt+b,得b=500, 4k+b=900,
解得k=100.
所以l1的函数表达式为y1=100 t+500;
设l2的函数表达式为y2=mt(m≠0),将(4,600)代入y2=mt,得4m=600,
解得m=150,
所以l2的函数表达式为y2=150 t. ( 8分)
(4)由(3)可知y1=100 t+500,y2=150 t.
①当100 t+500-150 t=100时,t=8;
②当150 t-(100 t+500)=100时,t=12.
所以当甲车与乙车相距100 km时,它们出发了8 h或12 h. (12分)
一 选择题(共10小题,每小题3分,共30分.每小题有四个选项,其中只有一个选项符合题意)
1.下列平面直角坐标系中的图象,不能表示y是x的函数的是 ( )
A B C D
2.有下列函数:①y=3πx;②y=8x-6;③y=;④y=-8x;⑤y=5x2-4x+1.其中是一次函数的有 ( )
A.4个 B.3个 C.2个 D.1个
3.对于函数y=-3x+1,下列结论正确的是 ( )
A.y随x的增大而增大
B.它的图象经过第一、二、三象限
C.它的图象必经过点(0,1)
D.当x=1时,y=2
4.用长为50的栏杆围成一个长为x宽为y的长方形,则y与x之间的函数关系为 ( )
A.y=25-x B.y=25+x C.y=50-x D.y=50+x
5.小明从家到学校,先匀速步行到公交车站,等了几分钟后坐上了公交车,公交车沿着公路匀速行驶一段时间后到达学校,则小明从家到学校的路程s与时间t之间的图象大致是 ( )
A B C D
6.在平面直角坐标系中,点A(2,m)关于y对称的点B在直线y=-x+1上,则m的值为 ( )
A.1 B.3 C.-3 D.2
7.如图,三个一次函数y=ax,y=bx,y=cx-3的图象如图所示,则a,b,c的大小关系是 ( )
A.b>a>c B.c>b>a
C.a>b>c D.c>a>b
8.下列图形中,能表示一次函数y=mx+n与正比例函数y=mnx(m,n为常数,且mn≠0)的图象的是 ( )
A B C D
9.直线y=kx+1沿着y轴向上平移b个单位后,经过点A(-2,0)和y轴上的一点B,若△ABO(O为坐标原点)的面积为4,则b的值为 ( )
A.4 B.2 C.3 D.1
10.如图(1),在长方形ABCD中,动点P从点B出发,沿路线B C D做匀速运动,图(2)是此运动过程中,△PAB的面积S与点P运动的时间t之间的函数图象的一部分,则长方形ABCD的周长是 ( )
图(1) 图(2)
A.6 B.8 C.10 D.12
二 填空题(共5小题,每小题3分,共15分)
11.某一次函数的图象过点(0,-1),且函数值y随x的增大而增大.请写出一个符合上述条件的函数表达式 .
12.一次函数y=mx+n的图象如图所示,则关于x的方程mx+n=0的解为 .
13.乐乐根据某个一次函数(y关于x的函数)的表达式填写了下表,其中有一格的数字不慎被墨汁遮住了,想想看,该空格里原来填的数是 .
x -2 -1 0 1
y 3 1 0
14.一种节能型轿车的油箱最多可装汽油50升,加满油后,油箱中的剩余油量y(升)与轿车行驶路程x(千米)之间的关系如图所示,为了行驶安全考虑,油箱中剩余油量不能低于6升,那么这辆节能型轿车加满油气后至多行驶 千米,就应该停车加油.
(第14题) (第15题)
15.正方形A1B1C1O,A2B2C2C1,A3B3C3C2……按如图所示的方式放置,已知点A1,A2,A3……和点C1,C2,C3……分别在直线y=x+1和x轴上,则点B6的坐标是 .
三 解答题(共5小题,共55分)
16.(10分)已知一次函数y=-3x+b,当x=3时,y=-8.
(1)求b的值,并求出函数图象与x轴的交点坐标;
(2)判断点P(-1,2)在不在该一次函数图象上.
17.(10分)已知y+1与x-3成正比例,且当x=-1时,y=3.
(1)求y与x之间的函数关系式;
(2)在坐标系中画出此函数图象;
(3)当y=2 023时,求x的值.
18.(11分)如图,在平面直角坐标系中,C(-4,0),直线AB分别交x轴,y轴的正半轴于点A,B,且满足OB=2,OA=1.
(1)求直线AB的表达式;
(2)在x轴上是否存在点D,使以点B,C,D为顶点的三角形的面积是△ABC面积的一半 若存在,请求出点D的坐标;若不存在,请说明理由.
19.(12分)甲、乙两个商场出售相同的某种商品,每件定价均为3 000元,并且多买都有一定的优惠.甲商场的优惠条件是:第一件按定价收费,其余每件优惠30%.乙商场的优惠条件是:每件优惠25%.设所买商品为x件时,甲商场收费为y1元,乙商场收费为y2元.
(1)分别求出y1,y2与x之间的函数关系式;
(2)当甲、乙两个商场的收费相同时,所买商品为多少件
(3)当所买商品为5件时,选择哪个商场更优惠 请说明理由.
20.(12分)如图,甲、乙两车分别从两地同时出发,且沿同一路线同向行驶,l1和l2分别表示甲、乙两车行驶的路程与时间的函数图象,请结合图象,解决下列问题:
(1)在刚出发时,甲车距乙车多少千米
(2)甲车与乙车的速度分别是多少
(3)分别求出l1,l2的函数表达式.
(4)当甲车与乙车相距100 km时,它们出发了多久
1.D 若y是x的函数,则对于自变量x的每一个值,因变量y都有唯一的值与它对应,故选D.
2.B y=3πx,y=8x-6,y=-8x是一次函数.y=的自变量的次数不为1,而为-1,不是一次函数.y=5x2-4x+1的自变量的最高次数不为1,而为2,不是一次函数.故选B.
3.C ∵一次函数y=-3x+1中的k=-3<0,b=1>0,∴y随x的增大而减小,且图象经过第一、二、四象限;∵当x=0时,y=1,∴它的图象必经过点(0,1);当x=1时,y=-2.故选C.
4.A 由题意得x+y=25,∴y=25-x.故选A.
5.B 小明从家匀速步行到公交车站,s的值随时间t的增大而增大,等了几分钟后坐上了公交车,在等车这个过程中,s的值不随时间t发生变化,公交车沿着公路匀速行驶一段时间后到达学校,s的值随时间t的增大而增大的较快,故选B.
6.B ∵点A(2,m)与点B关于y轴对称, ∴B(-2,m).∵点B在y=-x+1上,∴ m=-(-2)+1=3.故选B.
7.A 由题图可得a>0,b>0,c<0,且a
8.A ①当mn>0时,m,n同号,y=mnx的图象过第一、三象限,m,n同为正号时y=mx+n过第一、二、三象限;m,n同为负号时y=mx+n过第二、三、四象限.②当mn<0时,m,n异号,y=mnx的图象过第二、四象限,m>0,n<0时,y=mx+n过第一、三、四象限;m<0,n>0时,y=mx+n过第一、二、四象限.故选A.
9.C 直线y=kx+1沿着y轴向上平移b个单位后,得到y=kx+b+1,∴B(0,b+1),∴×2×(b+1)=4,解得b=3.故选C.
10.D 因为当点P到达点C时,△PAB的面积最大,此时△PAB的面积=×AB×BC=4.设动点P的速度为v,由题图(2)可得CD=AB=2v,BC=4v, 即×2v×4v=4,因为v>0所以v=1,所以AB=2,BC=4,所以长方形ABCD的周长=(2+4)×2=12.故选D.
11.y=x-1(y=kx-1,k>0即可) 【解析】由题意设y=kx-1,由函数值y随x的增大而增大,得到k>0,则满足上述条件的函数表达式可以为y=x-1.
12.x=-3 【解析】∵一次函数y=mx+n的图象与x轴的交点为(-3,0),∴当mx+n=0时,x=-3.
13.2 【解析】设一次函数的表达式为y=kx+b(k≠0),由该函数的图象经过点(0,1),(1,0),可得b=1,k=-1,所以该函数的表达式为y=-x+1.当x=-1时,y=2.
14.880 【解析】设y与x之间的关系式为y=kx+b(k≠0),将(0,50),(1 000,0)代入,得解得故y与x之间的关系式为y=-0.05x+50(0≤x≤1 000).把y=6代入,得6=-0.05x+50,解得x=880.
15.(63,32) 【解析】∵OC1=OA1=B1C1=A1B1=1,∴B1(1,1).∵点A2在直线y=x+1上,∴A2(1,2),∴B2C2=C1A2=C1C2=2,∴B2(3,2),同理可得B3(7,4),B4(15,8),B5(31,16),B6(63,32),∴点B6的坐标为(63,32).
16.【解题思路】(1)把已知值代入表达式可得关于b的方程,通过解方程,求得b的值.令y=0,求得x的值,可得函数图象与x轴的交点坐标.(2)把点P(-1,2)的坐标代入表达式,进行判断.
【参考答案】(1)把x=3,y=-8代入y=-3x+b,
得-3×3+b=-8,
∴b=1,
∴y=-3x+1. (3分)
令y=0,得-3x+1=0,
∴x=,
∴函数图象与x轴的交点坐标为(,0). (6分)
(2)把x=-1代入y=-3x+1,得y=4≠2,
∴点P不在该一次函数图象上. (10分)
17.【参考答案】(1)∵ y+1与x-3成正比例,
∴设y+1=k(x-3),
把x=-1,y=3代入,得4=-4k,
∴k=-1,
∴y与x之间的函数关系式为y+1=-(x-3), 即y=-x+2. (4分)
(2)令x=0, 则y=2,
令y=0, 则x=2,
如图,描点(0,2),(2,0), 连线即可. (8分)
(3)由题意得2 023=-x+2,解得x=-2 021. (10分)
18.【参考答案】(1)∵OB=2,OA=1,
∴点A的坐标为(1,0),点B的坐标为(0,2),
设直线AB的表达式为y=kx+2,
将点A的坐标代入,得0=k+2,
解得k=-2,
∴直线AB的表达式为y=-2x+2. (4分)
(2)存在.
设点D的坐标为(x,0),
∵A(1,0),B(0,2),C(-4,0),
∴AC=5,
∴S△ABC=×5×2=5.
∵S△BCD=S△ABC,
∴S△BCD=CD·OB=,
即|x-(-4)|×2=,
∴|x+4|=,
∴x=-或x=-,
∴点D的坐标为(-,0)或(-,0). (11分)
19.【解题思路】(1)根据两个商场的优惠条件列出函数关系式;(2)求收费相同时所买商品的件数,也就是求y1=y2时x的值;(3)当x=5时分别求出y1,y2的值,再进行比较即可.
【参考答案】(1)由题意,得y1=3 000×(1-30%)(x-1)+3 000=2 100x+900; (2分)
y2=3 000×(1-25%)x=2 250x. (4分)
(2)当y1=y2时,即2 100x+900=2 250x,解得x=6.
所以当甲、乙两个商场的收费相同时,所买商品为6件. (8分)
(3)选择乙商场更优惠.理由如下:
当x=5时,y1=2 100×5+900=11 400,
y2=2 250×5=11 250.
因为11 250<11 400,
所以当所买商品为5件时,选择乙商场更优惠. (12分)
20.【参考答案】(1)因为l1与y轴的交点为(0,500),l2与y轴的交点为(0,0),500-0=500(km),
所以在刚出发时,甲车距乙车500 km. (2分)
(2)(900-500)÷4=100(km/h),600÷4=150(km/h),所以甲车的速度是100 km/h,乙车的速度是150 km/h. (4分)
(3)设l1的函数表达式为y1=kt+b(k≠0),
将(0,500),(4,900)代入y1=kt+b,得b=500, 4k+b=900,
解得k=100.
所以l1的函数表达式为y1=100 t+500;
设l2的函数表达式为y2=mt(m≠0),将(4,600)代入y2=mt,得4m=600,
解得m=150,
所以l2的函数表达式为y2=150 t. ( 8分)
(4)由(3)可知y1=100 t+500,y2=150 t.
①当100 t+500-150 t=100时,t=8;
②当150 t-(100 t+500)=100时,t=12.
所以当甲车与乙车相距100 km时,它们出发了8 h或12 h. (12分)
同课章节目录
- 第一章 勾股定理
- 1 探索勾股定理
- 2 一定是直角三角形吗
- 3 勾股定理的应用
- 第二章 实数
- 1 认识无理数
- 2 平方根
- 3 立方根
- 4 估算
- 5 用计算器开方
- 6 实数
- 7 二次根式
- 第三章 位置与坐标
- 1 确定位置
- 2 平面直角坐标系
- 3 轴对称与坐标变化
- 第四章 一次函数
- 1 函数
- 2 一次函数与正比例函数
- 3 一次函数的图象
- 4 一次函数的应用
- 第五章 二元一次方程组
- 1 认识二元一次方程组
- 2 求解二元一次方程组
- 3 应用二元一次方程组——鸡免同笼
- 4 应用二元一次方程组——增收节支
- 5 应用二元一次方程组——里程碑上的数
- 6 二元一次方程与一次函数
- 7 用二元一次方程组确定一次函数表达式
- 8*三元一次方程组
- 第六章 数据的分析
- 1 平均数
- 2 中位数与众数
- 3 从统计图分析数据的集中趋势
- 4 数据的离散程度
- 第七章 平行线的证明
- 1 为什么要证明
- 2 定义与命题
- 3 平行线的判定
- 4 平行线的性质
- 5 三角形的内角和定理
