【核心素养目标】24.2.1 点与圆的位置关系 教案
文档属性
| 名称 | 【核心素养目标】24.2.1 点与圆的位置关系 教案 |
|
|
| 格式 | zip | ||
| 文件大小 | 1.7MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-07-11 00:00:00 | ||
图片预览



文档简介
中小学教育资源及组卷应用平台
24.2.1点与圆的位置关系 教学设计
课题 24.2.1点与圆的位置关系 单元 第24单元 学科 数学 年级 九年级(上)
教材分析 通过本节课的学习,渗透数形结合的思想和运动变化的观点教育,发展用数学知识解决实际问题的能力,激发学生学习数学的积极性。
核心素养分析 体现几何直观、推理能力核心素养,经历探索点与圆的位置关系过程,体会数学中分类思考问题的数学思想。
学习目标 1.掌握点和圆的三种位置关系,并会解决相关问题;2.能够过不在同一直线上的三个点作圆,理解三角形的外心和外接圆的概念;3.理解反证法.
重点 掌握点和圆的三种位置关系,能够过不在同一直线上的三个点作圆,理解三角形的外心和外接圆的概念.
难点
理解反证法.
教学过程
教学环节 教师活动 学生活动 设计意图
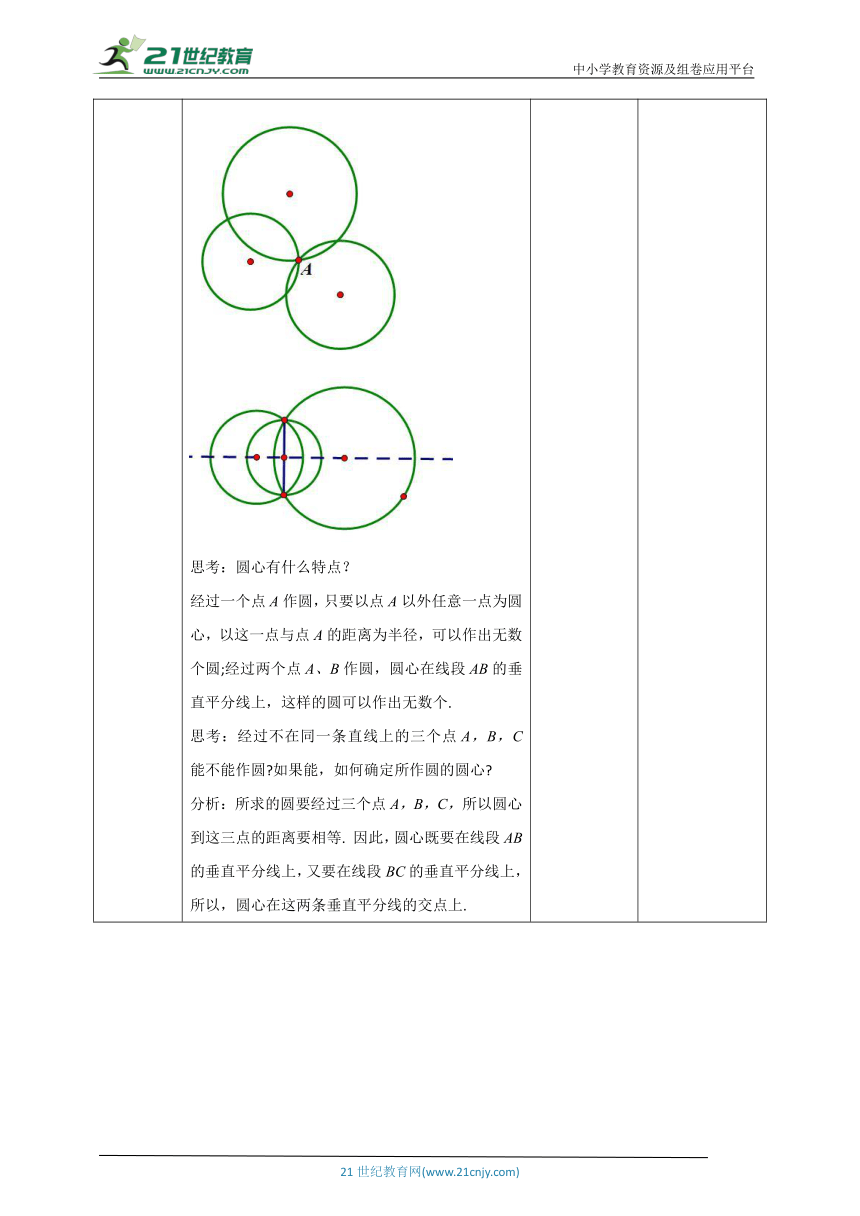
导入新课 一、创设情景,引出课题 复习回顾:在东京奥运会女子10米气步枪决赛中,中国选手杨倩以总分295分的成绩夺得金牌,获得中国首金.看电子靶的示意图,如果子弹看成点,靶看成圆,那么猜想一下点与圆有几种位置关系呢?环节一:探究点与圆的位置关系探究1:观察图中点A,点B,点C与⊙O的位置关系?点A在圆内,点B在圆上,点C在圆外.探究2:设⊙O半径为r,说出点A,点B,点C与圆心O的距离与半径的关系:OA r.思考:点与⊙O的位置关系和点与圆心的距离和半径大小有关吗?设⊙O的半径为r,点到圆心的距离为 d,则有:点在圆内 d < r ; 点在圆上 d =r ; 点在圆外 d > r ; 思考:如果已知点到圆心的距离和圆的半径大小,能否判断点和圆的位置关系?设⊙O的半径为r,点P到圆心的距离OP = d,则有:d < r 点在圆内d = r 点在圆上d > r 点在圆外小结:设⊙O的半径为r,点P到圆心的距离OP = d,则有:点P在圆内 d < r ; 点P在圆上 d = r ; 点P在圆外 d > r ; 符号 读作“等价于”,它表示从符号的左端可以得到右端,从右端也可以得到左端.射击靶图上,有一组以靶心为圆心的大小不同的圆,它们把靶图由内到外分成几个区域,这些区域用由高到低的环数表示,射击成绩用弹着点位置对应的环数表示. 弹着点与靶心的距离决定了它在哪个圆内,弹着点离靶心越近,它所在的区域就越靠内,对应环数也就越高,射击成绩越好.环节二:探究外接圆如何解决“破镜重圆”的问题? ( http: / / www.21cnjy.com )解决问题的关键是什么?(找圆心)探究3:圆是由圆心和半径决定的,那么经过一个已知点A能画出多少个圆?经过两个点A、B能画出多少个圆?思考:圆心有什么特点?经过一个点A作圆,只要以点A以外任意一点为圆心,以这一点与点A的距离为半径,可以作出无数个圆;经过两个点A、B作圆,圆心在线段AB的垂直平分线上,这样的圆可以作出无数个.思考:经过不在同一条直线上的三个点A,B,C能不能作圆 如果能,如何确定所作圆的圆心 分析:所求的圆要经过三个点A,B,C,所以圆心到这三点的距离要相等. 因此,圆心既要在线段AB的垂直平分线上,又要在线段BC的垂直平分线上,所以,圆心在这两条垂直平分线的交点上.作法:1.分别连接AB、BC;2. 分别作出线段AB、BC的垂直平分线l1和l2,设它们的交点为O ,则OA=OB=OC;3.以点O为圆心,OA(或OB、OC)为半径作圆,便可以作出经过A、B、C的圆.所以点O即为所求.不在同一直线上的三个点确定一个圆强调:(1)不在同一直线的三个点 (2)只有一个圆经过三角形的三个顶点可以做一个圆,这个圆叫做三角形的外接圆. 这个三角形叫做这个圆的内接三角形.外接圆的圆心是三角形三条边垂直平分线的交点,叫做这个三角形的外心.解决“破镜重圆”的问题: ( http: / / www.21cnjy.com )思考:锐角三角形、直角三角形、钝角三角形的外接圆的圆心如何确定?三角形的外心是三角形三条边垂直平分线的交点.环节三:反证法思考:经过同一条直线上的三个点能作出一个圆吗?如图,假设过同一条直线l上三点A,B,C可以作一个圆,设这个圆的圆心为P,那么点P既在线段AB的垂直平分线l1上,又在线段BC的垂直平分线l2上,即点P为l1与l2的交点,而l1⊥l,l2⊥l 这与我们以前学过的“过一点有且只有一条直线与已知直线垂直”相矛盾,所以过同一条直线上的三点不能作圆.先假设命题的结论不成立,然后经过推理得出矛盾(常与公理、定理、定义或已知条件相矛盾),由矛盾判定假设不正确,从而得到原命题成立,这种方法叫做反证法.当用直接法证较困难,可以用反证法来证明.反证法证明步骤:(1)假设命题的结论不成立,(2)经过推理,得出矛盾,(3)肯定原命题的结论正确. 思考自议创设情境,引起学生兴趣.通过观察,发现点和圆的位置关系.学生讨论解决“破镜重圆”问题的思路。教师出示问题,引导学生作图,分步骤引导学生思考“破镜重圆”问题与圆的关系。 鼓励学生通过自学探究得出结论.通过“破镜重圆”问题,激发学生好奇心,产生 ( http: / / www.21cnjy.com )探究问题的欲望,合作寻找解决问题的方法,锻炼学生的实践能力,培养学生分析为题的能力,巩固尺规作图的能力。
讲授新课 二、提炼概念1.锐角三角形的外心位于三角形内,2.直角三角形的外心位于直角三角形斜边的中点处,3.钝角三角形的外心位于三角形外.三、典例精讲 例1:画出由所有到已知点的距离大于或等于2cm并且小于或等于3cm的点组成的图形.例2:用反证法证明平行线的性质“两直线平行,同位角相等”。 ( http: / / www.21cnjy.com )证明:如果AB∥CD,那么∠1=∠2.假设∠1≠∠2,过点O作直线A’B’,使∠EOB’=∠2.根据“同位角相等,两直线平行”,可得A’B’ ∥CD。这样,过点O就有两条直线平行于CD,这与平行公理“过直线有且仅有一条直线与已知直线平行”矛盾。 在前面探究的基础上学生思考问题,进一步深入探究经过同一条直线上的三个点能否作出一个圆 通过深入探究,让学生在获得“不在同一直线上的三个点确定一个圆的结论”后趁热打铁,进一步探究规律,获得数学学习的成就感。通过总结获得“反证法”的定义和应用步骤。
课堂练习 四、巩固训练1.Rt△ABC中,∠C=90°,AC=3,BC=4,CD⊥AB于D点,以C为圆心,2.4cm为半径作⊙C,则D点与圆的位置关系是( )A.点D在⊙C上 B.点D在⊙C外 C.点D在⊙C内 D.无法确定A2.用反证法证明命题“三角形中必须有一个内角小于或等于60°”时,首先应假设这个三角形中( )A.有一个内角小于60° B.每一个内角都小于60°C.有一个内角大于60° D.每一个内角都大于60°.D3.判断下列说法是否正确:(1)任意的一个三角形一定有一个外接圆。 ( )(2)任意一个圆有且只有一个内接三角形。 ( )(3)经过三点一定可以确定一个圆。 ( )(4)三角形的外心到三角形各顶点的距离相等 ( )√,×,×,√4.在直角△ABC中,∠C=90°,BC=3,AC=4,以B为圆心,以BC为半径作⊙B,问点A、C及AB的中点D与圆有怎样的位置关系? 说明理由.证明:由题意知⊙B半径为3,所以点C在圆上.在直角△ABC中,∠C=90°,BC=3,AC=4根据勾股定理得,AB=5,所以点A在圆外.点D为AB中点,BD=2.5,所以点D在圆内.5.如图所示,残缺的破圆形轮片上,弦AB的垂直平分线交于点C,交弦AB于点D,已知AB=24cm,CD=8cm.(1)求作此残片所在的圆(不写作法,保留作图痕迹).(2)求(1)中所作圆的半径.解:(1)如图.(2)连接OA,设OA=OC=xcm.∵CO⊥AB,AB=24 cm,CD=8 cm,∴AD=12 cm,在Rt△AOD中,由勾股定理得OA2=AD2+OD2,即x2=122+(x-8)2,解得x=13,∴此残片所在圆的半径为13cm.
课堂小结 通过本节课的内容,你有哪些收获? ( http: / / www.21cnjy.com )
l1
l2
A
B
C
P
l
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://www.21cnjy.com/" 21世纪教育网(www.21cnjy.com)
24.2.1点与圆的位置关系 教学设计
课题 24.2.1点与圆的位置关系 单元 第24单元 学科 数学 年级 九年级(上)
教材分析 通过本节课的学习,渗透数形结合的思想和运动变化的观点教育,发展用数学知识解决实际问题的能力,激发学生学习数学的积极性。
核心素养分析 体现几何直观、推理能力核心素养,经历探索点与圆的位置关系过程,体会数学中分类思考问题的数学思想。
学习目标 1.掌握点和圆的三种位置关系,并会解决相关问题;2.能够过不在同一直线上的三个点作圆,理解三角形的外心和外接圆的概念;3.理解反证法.
重点 掌握点和圆的三种位置关系,能够过不在同一直线上的三个点作圆,理解三角形的外心和外接圆的概念.
难点
理解反证法.
教学过程
教学环节 教师活动 学生活动 设计意图
导入新课 一、创设情景,引出课题 复习回顾:在东京奥运会女子10米气步枪决赛中,中国选手杨倩以总分295分的成绩夺得金牌,获得中国首金.看电子靶的示意图,如果子弹看成点,靶看成圆,那么猜想一下点与圆有几种位置关系呢?环节一:探究点与圆的位置关系探究1:观察图中点A,点B,点C与⊙O的位置关系?点A在圆内,点B在圆上,点C在圆外.探究2:设⊙O半径为r,说出点A,点B,点C与圆心O的距离与半径的关系:OA
讲授新课 二、提炼概念1.锐角三角形的外心位于三角形内,2.直角三角形的外心位于直角三角形斜边的中点处,3.钝角三角形的外心位于三角形外.三、典例精讲 例1:画出由所有到已知点的距离大于或等于2cm并且小于或等于3cm的点组成的图形.例2:用反证法证明平行线的性质“两直线平行,同位角相等”。 ( http: / / www.21cnjy.com )证明:如果AB∥CD,那么∠1=∠2.假设∠1≠∠2,过点O作直线A’B’,使∠EOB’=∠2.根据“同位角相等,两直线平行”,可得A’B’ ∥CD。这样,过点O就有两条直线平行于CD,这与平行公理“过直线有且仅有一条直线与已知直线平行”矛盾。 在前面探究的基础上学生思考问题,进一步深入探究经过同一条直线上的三个点能否作出一个圆 通过深入探究,让学生在获得“不在同一直线上的三个点确定一个圆的结论”后趁热打铁,进一步探究规律,获得数学学习的成就感。通过总结获得“反证法”的定义和应用步骤。
课堂练习 四、巩固训练1.Rt△ABC中,∠C=90°,AC=3,BC=4,CD⊥AB于D点,以C为圆心,2.4cm为半径作⊙C,则D点与圆的位置关系是( )A.点D在⊙C上 B.点D在⊙C外 C.点D在⊙C内 D.无法确定A2.用反证法证明命题“三角形中必须有一个内角小于或等于60°”时,首先应假设这个三角形中( )A.有一个内角小于60° B.每一个内角都小于60°C.有一个内角大于60° D.每一个内角都大于60°.D3.判断下列说法是否正确:(1)任意的一个三角形一定有一个外接圆。 ( )(2)任意一个圆有且只有一个内接三角形。 ( )(3)经过三点一定可以确定一个圆。 ( )(4)三角形的外心到三角形各顶点的距离相等 ( )√,×,×,√4.在直角△ABC中,∠C=90°,BC=3,AC=4,以B为圆心,以BC为半径作⊙B,问点A、C及AB的中点D与圆有怎样的位置关系? 说明理由.证明:由题意知⊙B半径为3,所以点C在圆上.在直角△ABC中,∠C=90°,BC=3,AC=4根据勾股定理得,AB=5,所以点A在圆外.点D为AB中点,BD=2.5,所以点D在圆内.5.如图所示,残缺的破圆形轮片上,弦AB的垂直平分线交于点C,交弦AB于点D,已知AB=24cm,CD=8cm.(1)求作此残片所在的圆(不写作法,保留作图痕迹).(2)求(1)中所作圆的半径.解:(1)如图.(2)连接OA,设OA=OC=xcm.∵CO⊥AB,AB=24 cm,CD=8 cm,∴AD=12 cm,在Rt△AOD中,由勾股定理得OA2=AD2+OD2,即x2=122+(x-8)2,解得x=13,∴此残片所在圆的半径为13cm.
课堂小结 通过本节课的内容,你有哪些收获? ( http: / / www.21cnjy.com )
l1
l2
A
B
C
P
l
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://www.21cnjy.com/" 21世纪教育网(www.21cnjy.com)
同课章节目录
