人教版选修一2.5 实验:用单摆测定重力加速度 课件(34张PPT)
文档属性
| 名称 | 人教版选修一2.5 实验:用单摆测定重力加速度 课件(34张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 1.2MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(2019) | ||
| 科目 | 物理 | ||
| 更新时间 | 2022-07-10 19:54:45 | ||
图片预览






文档简介
(共34张PPT)
§2.5 实验:用单摆测量重力加速度
第二章 机械振动
曾经有个广东人到瑞士旅游,看到摆钟很漂亮,就买了一个回家,但是回到广东之后发现摆钟计时不准了,而在瑞士买的时候是很准的。后来就打电话投诉,但经过鉴定摆钟的质量是没有问题的。那问题出现在哪里?摆钟是走慢了还是走快了?如何进行校准呢?
理论上,与重力相关的物理现象都可以用来测量
地球上不同地方重力加速度g不同,同一个摆钟章到不同地方其摆动周期肯定不一样。
g在两极最大,赤道最小随着纬度的减小而减小,随高度增加而减小。
从瑞士到广东,纬度减小,g变小,摆钟摆动周期变大,摆钟走慢了,应把摆长变短。
那么,我们除了通过自由落体运动,还有哪些方法可以测量当地的重力加速度呢?
【思考】
惠更斯在推导出单摆的周期公式后,用一个单摆测出了巴黎的重力加速度。
那么我们也可以用同样的方法测量,请同学们设计一个实验,测量所在地区的重力加速度。
一、实验思路
单摆的周期公式:
测量原理:
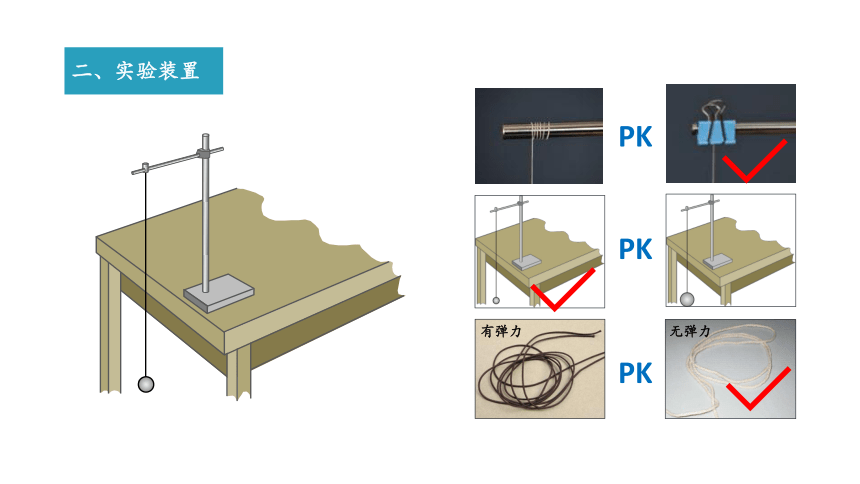
二、实验装置
PK
PK
PK
有弹力
无弹力
【小组讨论】
在实验中应如何选择摆线和摆球?
解答:选择较细的线,不可伸长且质量相对于摆球的质量可以忽略;选择半径小、质量大的摆球。
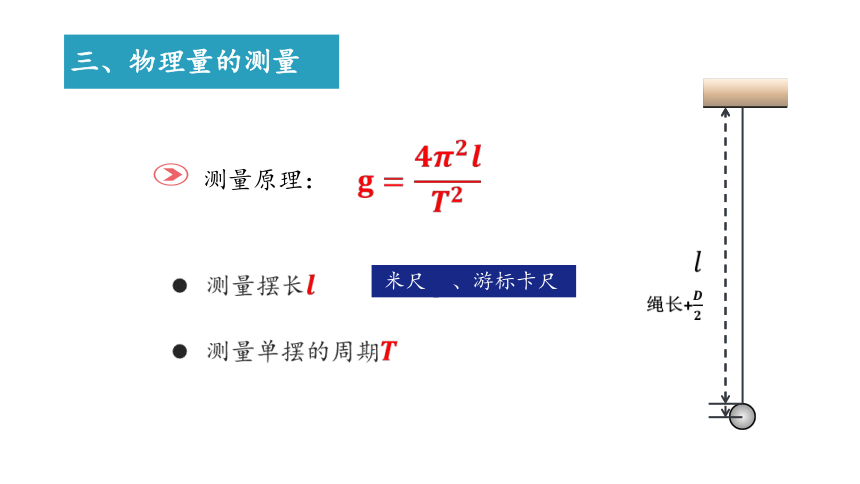
测量原理:
米尺
、游标卡尺
三、物理量的测量
0
5
10
0
1
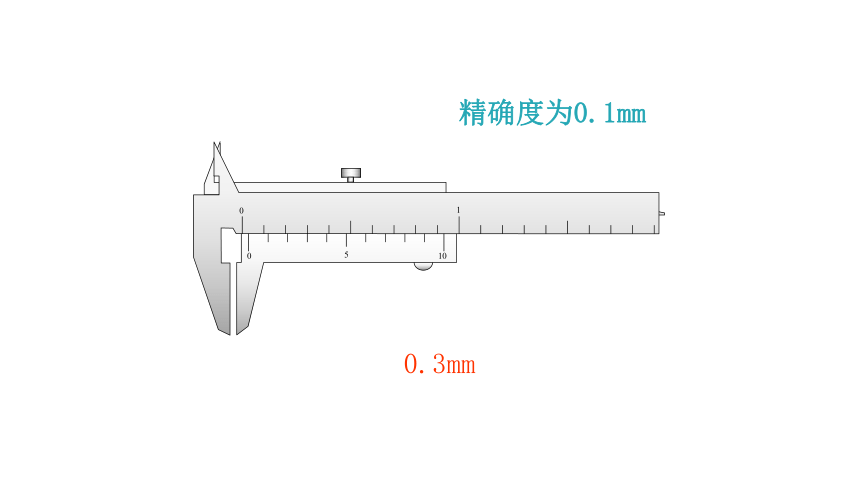
0.3mm
精确度为0.1mm
0
5
10
0
1
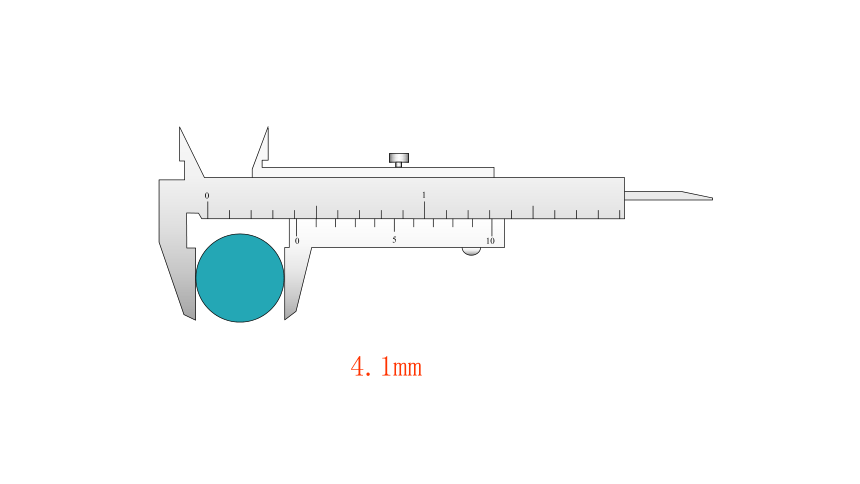
4.1mm
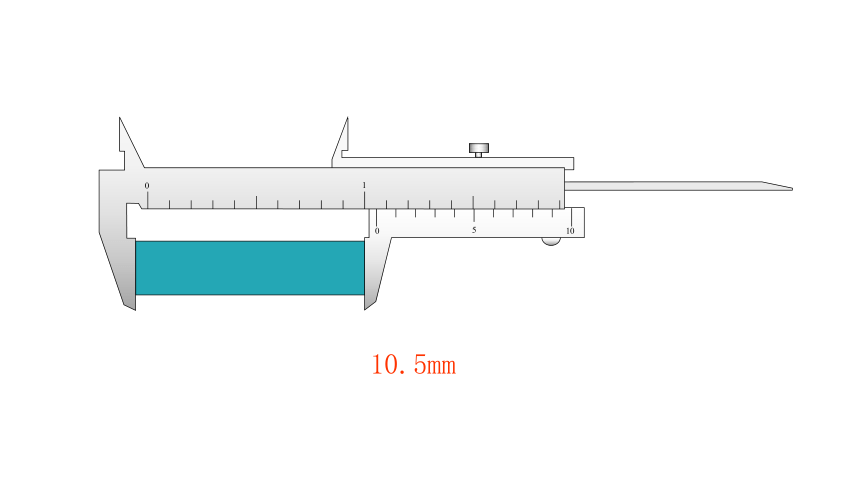
0
5
10
0
1
10.5mm
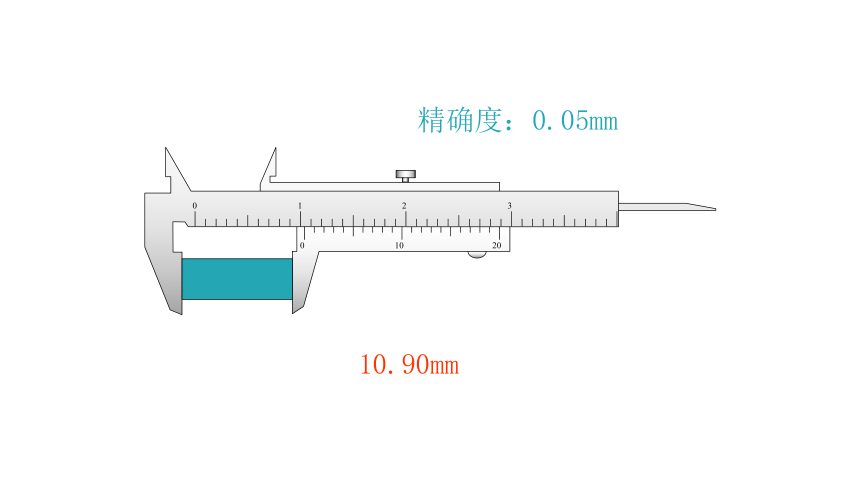
0
10
20
0
1
2
3
10.90mm
精确度:0.05mm
0
10
20
0
1
2
3
9.40mm
0
1
2
3
4
5
6
7
8
9
0
0
1
2
3
4
5
6
7
8
9
10
10.24mm
精确度:0.02mm
0
1
2
3
4
5
6
7
8
9
0
0
1
2
3
4
5
6
7
8
9
10
17.00mm
测量原理:
秒表
米尺
、游标卡尺
三、物理量的测量
、每次测量n个周期
多次测量
0
31
2
33
4
35
6
37
8
39
41
10
43
12
14
45
16
47
18
49
20
51
22
53
24
26
55
57
28
59
0
1
2
6
7
8
9
10
11
3
4
5
12
13
14
2分7.6秒
1分51.4秒
0
31
2
33
4
35
6
37
8
39
41
10
43
12
14
45
16
47
18
49
20
51
22
53
24
26
55
57
28
59
0
1
2
6
7
8
9
10
11
3
4
5
12
13
14
四、数据记录和处理
实验次数 摆长l/m 周期T/s 重力加速度g/(m·s-2 ) 重力加速度g的平均值/(m·s-2 )
1
2 3 1.平均值法:每改变一次摆长,将相应的l和T代入公式中求出g值,最后求出g的平均值。
设计如下所示实验表格
四、数据记录和处理
五、误差分析
主要来自于单摆模型本身是否符合要求,即悬点是否固定,摆球和摆长是否符合要求,最大摆角是否不超过5°,是否在同一竖直平面内摆动等。
(2)测长度和摆球直径时,读数也容易产生误差。秒表读数读到秒的十分位即可。
1.系统误差
2.偶然误差
(1)主要来自于时间测量,测量时间时要求从摆球通过平衡位置开始计时,在记次数时不能漏记或多记。同时应多次测量,再对多次测量结果求平均值。
六、注意事项
1.构成单摆的条件:摆线应选择细且不易伸长的线(长度1 m左右),小球应选用密度较大、体积较小的金属球(直径最好不超过2 cm),摆角要小,不超过5°。可通过估算振幅的办法掌握。
2.固定悬点:单摆悬线的上端不可随意卷在杆上,应夹紧在铁夹中,以免摆动时发生摆线下滑,摆长改变。
3.摆动方法:要使摆球在同一竖直面内摆动,不能形成圆锥摆,方法是将摆球拉到一定位置后由静止释放。
4.测摆长:摆长应是悬点到球心的距离,等于摆线长加上小球半径。
5.测周期:
(1)要从摆球经过平衡位置时开始计时。
(2)要测多次全振动的时间来计算周期,如在摆球过平衡位置时,开始计时并数零,以后摆球每过一次平衡位置数一个数,最后总计时为t,总数为n,则周期
反思改进
在用单摆测量重力加速度时,若所用的摆球质量分布不均匀,不能用摆线长加球半径得到单摆的摆长。我们采用如下方法解决这个问题:
由①②两式可求得当地的重力加速度
问题一
实验原理、操作和数据处理的考查
例题1(2021北京延庆高二期末)某实验小组的同学们用如图所示的装置做用单摆测量重力加速度的实验。
(1)实验时除用到秒表、刻度尺外,还应该用到下列器材中的 (选填选项前的字母,多选)。
A.长度为1 m左右的细线
B.长度为30 cm左右的细线
C.直径为1.8 cm的塑料球
D.直径为1.8 cm的钢球
(2)选择好器材,将符合实验要求的单摆悬挂在铁架台上,应采用图 (选填“甲”或“乙”)中所示的固定方式。
(3)将单摆正确悬挂后进行如下操作,其中正确的是 (选填选项前的字母,多选)。
A.测出摆线长作为单摆的摆长
B.把单摆从平衡位置拉开一个很小的角度释放,使之做简谐运动
C.在摆球经过平衡位置时开始计时
D.用秒表测量单摆完成1次全振动所用时间并作为单摆的周期
(4)测出悬点O到小球球心的距离(摆长)l及单摆完成n次全振动所用的时间t,则重力加速度g= (用l、n、t表示)。
(5)某同学多次改变单摆的摆长l并测得相应的周期T,他根据测量数据画出了如图所示的图像,但忘记在图中标明横坐标所代表的物理量。你认为横坐标所代表的物理量是 (选填“l2”“l”或“ ”)。
如果该图线的斜率为k,则重力加速度g的表达式g= (用k表示)。
(6)某同学测得的重力加速度数值小于当地的重力加速度的实际值,造成这一情况的原因可能是 (选填选项前的字母,多选)。
A.开始摆动时振幅较小
B.开始计时时,过早按下秒表
C.测量周期时,误将摆球29次全振动的时间记为30次全振动的时间
D.在测量完摆长之后悬挂点细线松动
解析 (1)实验过程中摆线不能太短,应选择长约1 m的细线作为摆线,故A正确,B错误;为减小实验误差,应选择密度大而体积小的球作为摆球,故应选择直径为1.8 cm的钢球作为摆球,不要选用直径为1.8 cm的塑料球,故C错误,D正确。
(2)在该实验的过程中,悬点要固定,应采用图乙中所示的固定方式。
(3)摆线长度与摆球半径之和是单摆的摆长,故A错误;单摆在小角度下的运动为简谐运动,把单摆从平衡位置拉开一个很小的角度释放,使之做简谐运动,故B正确;为减小测量误差,在摆球经过平衡位置时开始计时,故C正确;为减小测量误差,应测出n个周期的总时间t,然后求出周期为T= ,用单摆完成1次全振动所用时间作为单摆的周期实验误差较大,故D错误。
(6)由 ,g与振幅大小无关,故A错误;开始计时时,过早按下秒表,周期偏大,则g偏小,即测得的重力加速度数值小于当地的重力加速度的实际值,故B正确;测量周期时,误将摆球29次全振动的时间记为30次全振动的时间,则周期偏小,则g偏大,即测得的重力加速度数值大于当地的重力加速度的实际值,故C错误;单摆的悬挂点细线松动,而摆长已测量完毕,则g偏小,即测得的重力加速度数值小于当地的重力加速度的实际值,故D正确。
问题二
创新方案的设计
例题2.将一单摆装置竖直悬挂于某一深度为h(未知)且开口向下的小筒中(单摆的下部分露于筒外),如图甲所示,将悬线拉离平衡位置一个小角度后由静止释放,设单摆摆动过程中悬线不会碰到筒壁,如果本实验的长度测量工具只能测量出筒的下端口到摆球球心的距离L,并通过改变L而测出对应的摆动周期T,再以T2为纵轴、L为横轴作出函数关系图像,那么就可以通过此图像得出小筒的深度h和当地的重力加速度g。
(1)现有如下测量工具:A.时钟;B.停表;C.天平;D.毫米刻度尺。本实验所需的测量工具有 。 (2)如果实验中所得到的T2-L关系图像如图乙所示,那么真正的图像应该是a、b、c中的 。 (3)根据图像,小筒的深度为 ,当地的重力加速度大小为 。
思维导图
§2.5 实验:用单摆测量重力加速度
第二章 机械振动
曾经有个广东人到瑞士旅游,看到摆钟很漂亮,就买了一个回家,但是回到广东之后发现摆钟计时不准了,而在瑞士买的时候是很准的。后来就打电话投诉,但经过鉴定摆钟的质量是没有问题的。那问题出现在哪里?摆钟是走慢了还是走快了?如何进行校准呢?
理论上,与重力相关的物理现象都可以用来测量
地球上不同地方重力加速度g不同,同一个摆钟章到不同地方其摆动周期肯定不一样。
g在两极最大,赤道最小随着纬度的减小而减小,随高度增加而减小。
从瑞士到广东,纬度减小,g变小,摆钟摆动周期变大,摆钟走慢了,应把摆长变短。
那么,我们除了通过自由落体运动,还有哪些方法可以测量当地的重力加速度呢?
【思考】
惠更斯在推导出单摆的周期公式后,用一个单摆测出了巴黎的重力加速度。
那么我们也可以用同样的方法测量,请同学们设计一个实验,测量所在地区的重力加速度。
一、实验思路
单摆的周期公式:
测量原理:
二、实验装置
PK
PK
PK
有弹力
无弹力
【小组讨论】
在实验中应如何选择摆线和摆球?
解答:选择较细的线,不可伸长且质量相对于摆球的质量可以忽略;选择半径小、质量大的摆球。
测量原理:
米尺
、游标卡尺
三、物理量的测量
0
5
10
0
1
0.3mm
精确度为0.1mm
0
5
10
0
1
4.1mm
0
5
10
0
1
10.5mm
0
10
20
0
1
2
3
10.90mm
精确度:0.05mm
0
10
20
0
1
2
3
9.40mm
0
1
2
3
4
5
6
7
8
9
0
0
1
2
3
4
5
6
7
8
9
10
10.24mm
精确度:0.02mm
0
1
2
3
4
5
6
7
8
9
0
0
1
2
3
4
5
6
7
8
9
10
17.00mm
测量原理:
秒表
米尺
、游标卡尺
三、物理量的测量
、每次测量n个周期
多次测量
0
31
2
33
4
35
6
37
8
39
41
10
43
12
14
45
16
47
18
49
20
51
22
53
24
26
55
57
28
59
0
1
2
6
7
8
9
10
11
3
4
5
12
13
14
2分7.6秒
1分51.4秒
0
31
2
33
4
35
6
37
8
39
41
10
43
12
14
45
16
47
18
49
20
51
22
53
24
26
55
57
28
59
0
1
2
6
7
8
9
10
11
3
4
5
12
13
14
四、数据记录和处理
实验次数 摆长l/m 周期T/s 重力加速度g/(m·s-2 ) 重力加速度g的平均值/(m·s-2 )
1
2 3 1.平均值法:每改变一次摆长,将相应的l和T代入公式中求出g值,最后求出g的平均值。
设计如下所示实验表格
四、数据记录和处理
五、误差分析
主要来自于单摆模型本身是否符合要求,即悬点是否固定,摆球和摆长是否符合要求,最大摆角是否不超过5°,是否在同一竖直平面内摆动等。
(2)测长度和摆球直径时,读数也容易产生误差。秒表读数读到秒的十分位即可。
1.系统误差
2.偶然误差
(1)主要来自于时间测量,测量时间时要求从摆球通过平衡位置开始计时,在记次数时不能漏记或多记。同时应多次测量,再对多次测量结果求平均值。
六、注意事项
1.构成单摆的条件:摆线应选择细且不易伸长的线(长度1 m左右),小球应选用密度较大、体积较小的金属球(直径最好不超过2 cm),摆角要小,不超过5°。可通过估算振幅的办法掌握。
2.固定悬点:单摆悬线的上端不可随意卷在杆上,应夹紧在铁夹中,以免摆动时发生摆线下滑,摆长改变。
3.摆动方法:要使摆球在同一竖直面内摆动,不能形成圆锥摆,方法是将摆球拉到一定位置后由静止释放。
4.测摆长:摆长应是悬点到球心的距离,等于摆线长加上小球半径。
5.测周期:
(1)要从摆球经过平衡位置时开始计时。
(2)要测多次全振动的时间来计算周期,如在摆球过平衡位置时,开始计时并数零,以后摆球每过一次平衡位置数一个数,最后总计时为t,总数为n,则周期
反思改进
在用单摆测量重力加速度时,若所用的摆球质量分布不均匀,不能用摆线长加球半径得到单摆的摆长。我们采用如下方法解决这个问题:
由①②两式可求得当地的重力加速度
问题一
实验原理、操作和数据处理的考查
例题1(2021北京延庆高二期末)某实验小组的同学们用如图所示的装置做用单摆测量重力加速度的实验。
(1)实验时除用到秒表、刻度尺外,还应该用到下列器材中的 (选填选项前的字母,多选)。
A.长度为1 m左右的细线
B.长度为30 cm左右的细线
C.直径为1.8 cm的塑料球
D.直径为1.8 cm的钢球
(2)选择好器材,将符合实验要求的单摆悬挂在铁架台上,应采用图 (选填“甲”或“乙”)中所示的固定方式。
(3)将单摆正确悬挂后进行如下操作,其中正确的是 (选填选项前的字母,多选)。
A.测出摆线长作为单摆的摆长
B.把单摆从平衡位置拉开一个很小的角度释放,使之做简谐运动
C.在摆球经过平衡位置时开始计时
D.用秒表测量单摆完成1次全振动所用时间并作为单摆的周期
(4)测出悬点O到小球球心的距离(摆长)l及单摆完成n次全振动所用的时间t,则重力加速度g= (用l、n、t表示)。
(5)某同学多次改变单摆的摆长l并测得相应的周期T,他根据测量数据画出了如图所示的图像,但忘记在图中标明横坐标所代表的物理量。你认为横坐标所代表的物理量是 (选填“l2”“l”或“ ”)。
如果该图线的斜率为k,则重力加速度g的表达式g= (用k表示)。
(6)某同学测得的重力加速度数值小于当地的重力加速度的实际值,造成这一情况的原因可能是 (选填选项前的字母,多选)。
A.开始摆动时振幅较小
B.开始计时时,过早按下秒表
C.测量周期时,误将摆球29次全振动的时间记为30次全振动的时间
D.在测量完摆长之后悬挂点细线松动
解析 (1)实验过程中摆线不能太短,应选择长约1 m的细线作为摆线,故A正确,B错误;为减小实验误差,应选择密度大而体积小的球作为摆球,故应选择直径为1.8 cm的钢球作为摆球,不要选用直径为1.8 cm的塑料球,故C错误,D正确。
(2)在该实验的过程中,悬点要固定,应采用图乙中所示的固定方式。
(3)摆线长度与摆球半径之和是单摆的摆长,故A错误;单摆在小角度下的运动为简谐运动,把单摆从平衡位置拉开一个很小的角度释放,使之做简谐运动,故B正确;为减小测量误差,在摆球经过平衡位置时开始计时,故C正确;为减小测量误差,应测出n个周期的总时间t,然后求出周期为T= ,用单摆完成1次全振动所用时间作为单摆的周期实验误差较大,故D错误。
(6)由 ,g与振幅大小无关,故A错误;开始计时时,过早按下秒表,周期偏大,则g偏小,即测得的重力加速度数值小于当地的重力加速度的实际值,故B正确;测量周期时,误将摆球29次全振动的时间记为30次全振动的时间,则周期偏小,则g偏大,即测得的重力加速度数值大于当地的重力加速度的实际值,故C错误;单摆的悬挂点细线松动,而摆长已测量完毕,则g偏小,即测得的重力加速度数值小于当地的重力加速度的实际值,故D正确。
问题二
创新方案的设计
例题2.将一单摆装置竖直悬挂于某一深度为h(未知)且开口向下的小筒中(单摆的下部分露于筒外),如图甲所示,将悬线拉离平衡位置一个小角度后由静止释放,设单摆摆动过程中悬线不会碰到筒壁,如果本实验的长度测量工具只能测量出筒的下端口到摆球球心的距离L,并通过改变L而测出对应的摆动周期T,再以T2为纵轴、L为横轴作出函数关系图像,那么就可以通过此图像得出小筒的深度h和当地的重力加速度g。
(1)现有如下测量工具:A.时钟;B.停表;C.天平;D.毫米刻度尺。本实验所需的测量工具有 。 (2)如果实验中所得到的T2-L关系图像如图乙所示,那么真正的图像应该是a、b、c中的 。 (3)根据图像,小筒的深度为 ,当地的重力加速度大小为 。
思维导图
