苏教版高中数学必修1第6章 §6.1 幂函数 学案(Word版含答案)
文档属性
| 名称 | 苏教版高中数学必修1第6章 §6.1 幂函数 学案(Word版含答案) |

|
|
| 格式 | docx | ||
| 文件大小 | 2.5MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏教版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-07-10 21:09:39 | ||
图片预览




文档简介
学习目标 1.了解幂函数的概念.2.掌握y=xα的图象与性质.3.理解和掌握幂函数在第一象限的分类特征,能运用数形结合的方法处理幂函数的有关问题.
导语
同学们,我们说要学好数学,要先了解它的发展史,比如我们今天要学习的幂函数,“幂”其原意是遮盖东西用的布,后来引申为面积.《九章算术》刘徽注:“凡广纵相乘谓之幂.”后来又推广引申为多次乘方的结果.到了清明时代,既称面积为幂,也称平方或立方为幂.清末之后,幂逐渐开始专指乘方概念.
一、幂函数的概念
问题1 下面几个实例,观察它们得出的函数解析式,有什么共同特征?
(1)如果张红以1元/kg的价格购买了某种蔬菜ω kg,那么她需要支付p=ω元,这里p是ω的函数;
(2)如果正方形的边长为a,那么正方形的面积S=a2,这里S是a的函数;
(3)如果立方体的棱长为b,那么立方体的体积V=b3,这里V是b的函数;
(4)如果一个正方形场地的面积为S,那么这个正方形的边长c=,即c=,这里c是S的函数;
(5)如果某人t s内骑车行进了1 km,那么他骑车的平均速度v= km/s,即v=t-1,这里v是t的函数.
提示 这些函数的解析式都具有指数幂的形式,而且都是以幂的底数为自变量,幂的指数都是常数.
知识梳理
幂函数的概念
一般地,我们把形如y=xα的函数称为幂函数,其中x是自变量,α是常数.
注意点:
(1)自变量前的系数是1;
(2)幂的系数为1;
(3)α是任意常数;
(4)函数的定义域与α有关.
例1 (1)在函数y=,y=2x2,y=x2+x,y=1中,幂函数的个数为( )
A.0 B.1 C.2 D.3
答案 B
解析 ∵y==x-2,∴是幂函数;y=2x2由于出现系数2,因此不是幂函数;y=x2+x是两项和的形式,不是幂函数;y=1=x0(x≠0),可以看出,常函数y=1的图象比幂函数y=x0的图象多了一个点(0,1),所以常函数y=1不是幂函数.
(2)已知y=+2n-3是幂函数,求m,n的值.
解 由题意得
解得m=-3或1,n=.
反思感悟 幂函数的判断及应用
(1)判断一个函数是否为幂函数的依据是该函数是否为y=xα(α为常数)的形式,需满足:①指数为常数,②底数为自变量,③xα的系数为1.
(2)若一个函数为幂函数,则该函数也必具有y=xα(α为常数)这一形式.
跟踪训练1 若函数f(x)是幂函数,且满足f(4)=16,则f(-4)=________.
答案 16
解析 设f(x)=xα,∵f(4)=16,∴4α=16,解得α=2,∴f(x)=x2,∴f(-4)=(-4)2=16.
二、幂函数的图象与性质
问题2 根据之前所学的函数概念与性质,我们应该从哪些方面来研究幂函数呢?
提示 根据函数解析式先求出函数的定义域,然后画出函数图象,再利用图象和解析式研究函数的单调性、最值、值域、奇偶性、对称性等问题.
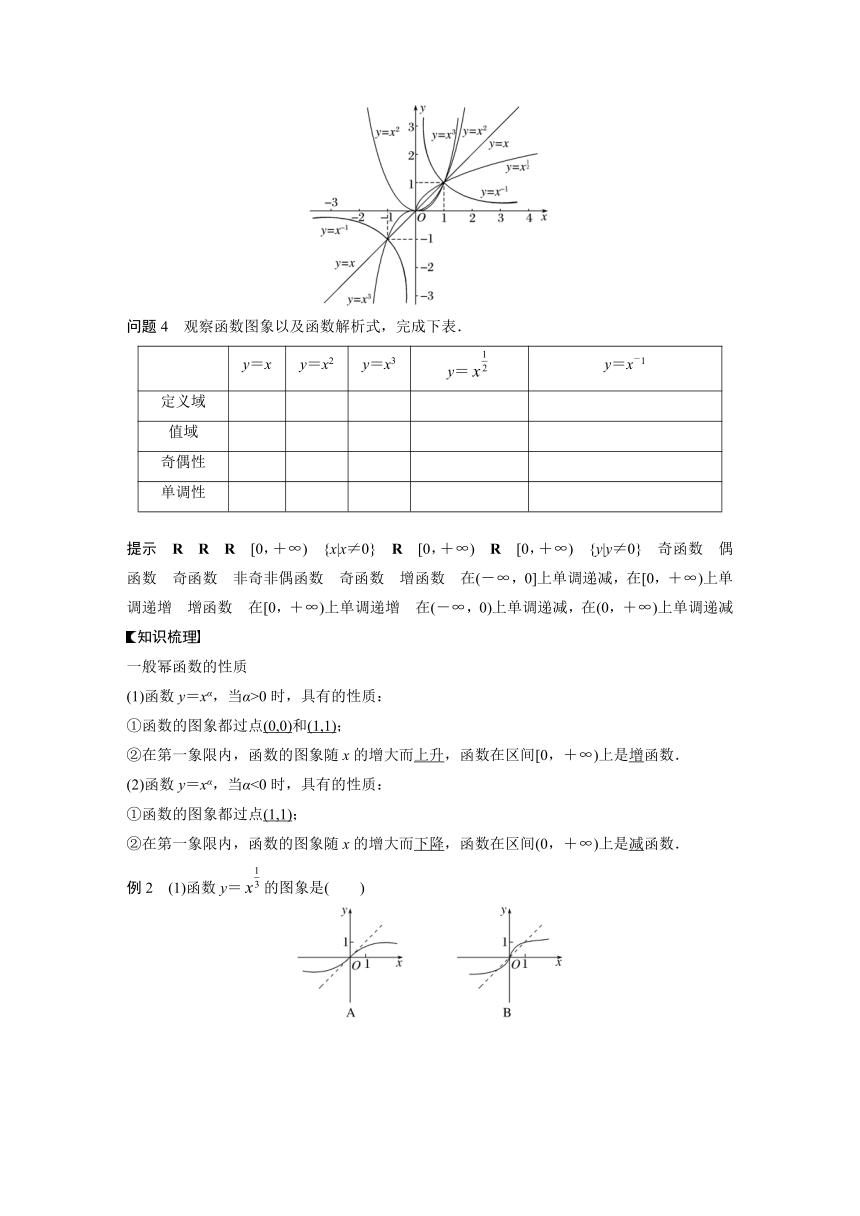
问题3 你能在同一坐标系下作出y=x,y=x2,y=x3,y=,y=x-1这五个函数的图象吗?
提示
问题4 观察函数图象以及函数解析式,完成下表.
y=x y=x2 y=x3 y= y=x-1
定义域
值域
奇偶性
单调性
提示 R R R [0,+∞) {x|x≠0} R [0,+∞) R [0,+∞) {y|y≠0} 奇函数 偶函数 奇函数 非奇非偶函数 奇函数 增函数 在(-∞,0]上单调递减,在[0,+∞)上单调递增 增函数 在[0,+∞)上单调递增 在(-∞,0)上单调递减,在(0,+∞)上单调递减
知识梳理
一般幂函数的性质
(1)函数y=xα,当α>0时,具有的性质:
①函数的图象都过点(0,0)和(1,1);
②在第一象限内,函数的图象随x的增大而上升,函数在区间[0,+∞)上是增函数.
(2)函数y=xα,当α<0时,具有的性质:
①函数的图象都过点(1,1);
②在第一象限内,函数的图象随x的增大而下降,函数在区间(0,+∞)上是减函数.
例2 (1)函数y=的图象是( )
(2)如图所示,图中的曲线是幂函数y=xn在第一象限的图象,已知n取±2,±四个值,则相应于C1,C2,C3,C4的n依次为( )
A.-2,-,,2 B.2,,-,-2
C.-,-2,2, D.2,,-2,-
答案 (1)B (2)B
解析 (1)∵当x>1时,x>;当x=1时,x=,所以A,C,D均不对,选B.
(2)根据幂函数y=xn的性质,在第一象限内的图象当n>0时,n越大,y=xn递增速度越快,故C1的n=2,C2的n=;当n<0时,|n|越大,曲线越陡峭,所以曲线C3的n=-,曲线C4的n=-2,故选B.
反思感悟 (1)幂函数图象的画法
①确定幂函数在第一象限内的图象:先根据α的取值,确定幂函数y=xα在第一象限内的图象.
②确定幂函数在其他象限内的图象:根据幂函数的定义域及奇偶性确定幂函数f(x)在其他象限内的图象.
(2)解决与幂函数有关的综合性问题的方法
首先要考虑幂函数的概念,对于幂函数y=xα(α是常数),由于α的取值不同,所以相应幂函数的单调性和奇偶性也不同.同时,注意分类讨论思想的应用.
跟踪训练2 如图是幂函数y=xm与y=xn在第一象限内的图象,则( )
A.-1B.n<-1,0C.-11
D.n<-1,m>1
答案 B
解析 由于y=xm在(0,+∞)上是增函数,且为上凸函数,故0三、幂函数的图象与性质的应用
例3 比较下列各组数中两个数的大小:
(1)0.5与0.5;
(2)-1与-1;
(3)与.
解 (1)∵幂函数y=x0.5在(0,+∞)上是增函数,又>,
∴0.5>0.5.
(2)∵幂函数y=x-1在(-∞,0)上是减函数,
又-<-,
∴-1>-1.
(3)∵函数y1=在(0,+∞)上是增函数,
又>1,∴=1.
又∵函数y2=在(0,+∞)上是增函数,且<1,∴=1,
∴.
反思感悟 比较幂值大小的方法
(1)若两个幂值的指数相同或可化为两个指数相同的幂值时,则可构造函数,利用幂函数的单调性比较大小.
(2)若底数、指数均不同,则考虑用中间值法比较大小,这里的中间值可以是“0”或“1”.
跟踪训练3 比较下列各组数中两个数的大小:
(1)-0.3与-0.3;
(2)-3.143与-π3.
解 (1)∵y=x-0.3在(0,+∞)上是减函数,
又>,
∴-0.3<-0.3.
(2)∵y=x3是R上的增函数,且3.14<π,
∴3.143<π3,∴-3.143>-π3.
1.知识清单:
(1)幂函数的定义.
(2)几个常见幂函数的图象.
(3)幂函数的性质.
2.方法归纳:待定系数法、数形结合法.
3.常见误区:易忽略幂函数的概念.
1.已知幂函数y=f(x)的图象经过点,则f(2)等于( )
A. B.2 C. D.
答案 A
解析 设幂函数为y=xα,
∵幂函数的图象经过点,
∴=4α,∴α=-1,∴y=x-1,
∴f(2)=2-1=.
2.设α∈,则使函数y=xα的定义域是R,且为奇函数的所有α的值是( )
A.1,3 B.-1,1
C.-1,3 D.-1,1,3
答案 A
解析 当α=-1时,函数y=x-1的定义域是{x|x≠0},且为奇函数;当α=1时,函数y=x的定义域是R,且为奇函数;当α=时,函数y=的定义域是{x|x≥0},且为非奇非偶函数;当α=3时,函数y=x3的定义域是R,且为奇函数.
3.函数y=的图象是( )
答案 C
解析 ∵函数y=的定义域为[0,+∞),
∴它是非奇非偶函数,故排除A,B选项.
又>1,
∴图象在区间[0,1]上是下凸的,故排除D选项.
4.0.23-2.3与0.24-2.3的大小关系是___________________________.
答案 0.23-2.3>0.24-2.3
解析 因为函数y=x-2.3在(0,+∞)上是减函数,且0.23<0.24,
所以0.23-2.3>0.24-2.3.
1.幂函数的图象过点(16,4),则该幂函数的解析式是( )
A.y=x-1 B.y=
C.y=x2 D.y=x3
答案 B
解析 设f(x)=xα,则16α=4,
∴α=,∴f(x)=.
2.下列函数中,既是偶函数,又在区间(0,+∞)上是增函数的是( )
A.y= B.y=x-1
C.y=x2 D.y=x
答案 C
解析 由于y=x-1和y=x都是奇函数,故B,D不满足题意.y=在(0,+∞)上是增函数,但不是偶函数,故A不满足题意.y=x2为偶函数,且在(0,+∞)上是增函数,故C满足题意.
3.已知函数f(x)=,若0A.f(a)B.f C.f(a)D.f 答案 C
解析 因为函数f(x)=在(0,+∞)上是增函数,
又0故f(a)4.函数y=-1的图象关于x轴对称的图象大致是( )
答案 B
解析 y=的图象位于第一象限,且为增函数,所以函数图象是上升的,函数y=-1的图象可看作是由y=的图象向下平移一个单位长度得到的(如选项A中的图所示),则y=-1的图象关于x轴对称的图象即为选项B.
5.(多选)已知幂函数f(x)的图象经过点,则幂函数f(x)具有的性质是( )
A.在其定义域上为增函数
B.在(0,+∞)上是减函数
C.奇函数
D.定义域为R
答案 BC
解析 设幂函数f(x)=xα(α为常数),因为幂函数图象过点,所以f(x)=,所以由f(x)的性质知,定义域为{x∈R|x≠0},f(x)是奇函数,在(-∞,0),(0,+∞)上均是减函数.
6.(多选)下列命题不正确的是( )
A.幂函数的图象都经过(0,0),(1,1)两点
B.当n=0时,函数y=xn的图象是一条直线
C.如果两个幂函数的图象有三个交点,那么这两个函数一定相同
D.如果幂函数为偶函数,则图象一定经过点(-1,1)
答案 ABC
解析 对于A,幂函数的图象都经过点(1,1),当y=xn中n≤0时,不过点(0,0),故A不正确;对于B,当n=0时,幂函数y=xn的图象是直线y=1除去点(0,1),故B不正确;对于C,当两个幂函数的图象有三个交点时,两函数不一定相同,如y=x与y=x3的图象有三个交点,但这两个函数不相同,故C不正确;对于D,因为幂函数的图象都经过点(1,1),所以若幂函数为偶函数,其图象一定经过点(-1,1),故D正确.
7.已知2.4α>2.5α,则α的取值范围是________.
答案 α<0
解析 因为0<2.4<2.5,而2.4α>2.5α,
所以y=xα在(0,+∞)上是减函数.故α<0.
8.若幂函数y=(m2-2m-2)x-4m-2在x∈(0,+∞)上为减函数,则实数m的值是________.
答案 3
解析 因为函数y=(m2-2m-2)x-4m-2既是幂函数又是(0,+∞)上的减函数,
所以
解得m=3.
9.已知函数f(x)=(m2+2m)·,m为何值时,函数f(x)是(1)正比例函数;(2)反比例函数;(3)幂函数.
解 (1)若函数f(x)为正比例函数,
则∴m=1.
(2)若函数f(x)为反比例函数,
则∴m=-1.
(3)若函数f(x)为幂函数,则m2+2m=1,
∴m=-1±.
10.比较下列各组数的大小:
(1)和;
(2)和.
解 (1)函数y=在(0,+∞)上是减函数,
又3<3.2,所以
(2)函数y=在(0,+∞)上是增函数,
而>,所以
11.函数f(x)=+b-3是幂函数,则下列结论正确的是( )
A.f(a)>f(b) B.f(a)C.f(a)=f(b) D.以上都不对
答案 A
解析 ∵f(x)为幂函数,
∴解得
∴f(x)=,
∴f(x)在(0,+∞)上是增函数,且a>b>0,
∴f(a)>f(b).
12.已知幂函数y=(m∈Z)的图象与x轴和y轴没有交点,且关于y轴对称,则m等于( )
A.1 B.0,2
C.-1,1,3 D.0,1,2
答案 C
解析 ∵幂函数y=(m∈Z)的图象与x轴和y轴没有交点,且关于y轴对称,
∴m2-2m-3≤0,且m2-2m-3(m∈Z)为偶数,
由m2-2m-3≤0,得-1≤m≤3,
又m∈Z,∴m=-1,0,1,2,3.
当m=-1时,m2-2m-3=1+2-3=0,为偶数,符合题意;
当m=0时,m2-2m-3=-3,为奇数,不符合题意;
当m=1时,m2-2m-3=1-2-3=-4,为偶数,符合题意;
当m=2时,m2-2m-3=4-4-3=-3,为奇数,不符合题意;
当m=3时,m2-2m-3=9-6-3=0,为偶数,符合题意.
综上所述,m=-1,1,3.
13.若,则实数m的取值范围为________.
答案
解析 因为y=在定义域[0,+∞)上是增函数,所以
解得-1≤m<.
故m的取值范围为.
14.给出下面四个条件:①f(m+n)=f(m)+f(n);②f(m+n)=f(m)·f(n);③f(mn)=f(m)·f(n);④f(mn)=f(m)+f(n).如果m,n是幂函数y=f(x)定义域内的任意两个值,那么幂函数y=f(x)一定满足的条件的序号为________.
答案 ③
解析 设f(x)=xα,则f(m+n)=(m+n)α,
f(m)+f(n)=mα+nα,
f(m)·f(n)=mα·nα=(mn)α,
f(mn)=(mn)α,
所以f(mn)=f(m)·f(n)一定成立,其他三个不一定成立.
15.(多选)给出下列幂函数,其中满足条件f <(x1>x2>0)的函数的是( )
A.f(x)=x B.f(x)=x2
C.f(x)=x3 D.f(x)=
答案 BC
解析 A.函数f(x)=x的图象是一条直线,
故当x1>x2>0时,
f =;
B.函数f(x)=x2的图象是下凸形曲线,
故当x1>x2>0时,
f <;
C.在第一象限,函数f(x)=x3的图象是下凸形曲线,故当x1>x2>0时,
f <;
D.函数f(x)=的图象是上凸形曲线,
故当x1>x2>0时,
f >.
16.已知幂函数f(x)=在(0,+∞)上是增函数,函数g(x)=2x-k.
(1)求m的值;
(2)当x∈[1,2]时,记f(x),g(x)的值域分别为集合A,B,若A∪B=A,求实数k的取值范围.
解 (1)依题意,得(m-1)2=1,
解得m=0或m=2.
当m=2时,f(x)=x-2在(0,+∞)上是减函数,与题设矛盾,舍去,∴m=0.
(2)由(1)可知f(x)=x2.
当x∈[1,2]时,f(x),g(x)是增函数,
∴A=[1,4],B=[2-k,4-k].
∵A∪B=A,∴B A,
∴ 0≤k≤1.
∴实数k的取值范围是[0,1].
导语
同学们,我们说要学好数学,要先了解它的发展史,比如我们今天要学习的幂函数,“幂”其原意是遮盖东西用的布,后来引申为面积.《九章算术》刘徽注:“凡广纵相乘谓之幂.”后来又推广引申为多次乘方的结果.到了清明时代,既称面积为幂,也称平方或立方为幂.清末之后,幂逐渐开始专指乘方概念.
一、幂函数的概念
问题1 下面几个实例,观察它们得出的函数解析式,有什么共同特征?
(1)如果张红以1元/kg的价格购买了某种蔬菜ω kg,那么她需要支付p=ω元,这里p是ω的函数;
(2)如果正方形的边长为a,那么正方形的面积S=a2,这里S是a的函数;
(3)如果立方体的棱长为b,那么立方体的体积V=b3,这里V是b的函数;
(4)如果一个正方形场地的面积为S,那么这个正方形的边长c=,即c=,这里c是S的函数;
(5)如果某人t s内骑车行进了1 km,那么他骑车的平均速度v= km/s,即v=t-1,这里v是t的函数.
提示 这些函数的解析式都具有指数幂的形式,而且都是以幂的底数为自变量,幂的指数都是常数.
知识梳理
幂函数的概念
一般地,我们把形如y=xα的函数称为幂函数,其中x是自变量,α是常数.
注意点:
(1)自变量前的系数是1;
(2)幂的系数为1;
(3)α是任意常数;
(4)函数的定义域与α有关.
例1 (1)在函数y=,y=2x2,y=x2+x,y=1中,幂函数的个数为( )
A.0 B.1 C.2 D.3
答案 B
解析 ∵y==x-2,∴是幂函数;y=2x2由于出现系数2,因此不是幂函数;y=x2+x是两项和的形式,不是幂函数;y=1=x0(x≠0),可以看出,常函数y=1的图象比幂函数y=x0的图象多了一个点(0,1),所以常函数y=1不是幂函数.
(2)已知y=+2n-3是幂函数,求m,n的值.
解 由题意得
解得m=-3或1,n=.
反思感悟 幂函数的判断及应用
(1)判断一个函数是否为幂函数的依据是该函数是否为y=xα(α为常数)的形式,需满足:①指数为常数,②底数为自变量,③xα的系数为1.
(2)若一个函数为幂函数,则该函数也必具有y=xα(α为常数)这一形式.
跟踪训练1 若函数f(x)是幂函数,且满足f(4)=16,则f(-4)=________.
答案 16
解析 设f(x)=xα,∵f(4)=16,∴4α=16,解得α=2,∴f(x)=x2,∴f(-4)=(-4)2=16.
二、幂函数的图象与性质
问题2 根据之前所学的函数概念与性质,我们应该从哪些方面来研究幂函数呢?
提示 根据函数解析式先求出函数的定义域,然后画出函数图象,再利用图象和解析式研究函数的单调性、最值、值域、奇偶性、对称性等问题.
问题3 你能在同一坐标系下作出y=x,y=x2,y=x3,y=,y=x-1这五个函数的图象吗?
提示
问题4 观察函数图象以及函数解析式,完成下表.
y=x y=x2 y=x3 y= y=x-1
定义域
值域
奇偶性
单调性
提示 R R R [0,+∞) {x|x≠0} R [0,+∞) R [0,+∞) {y|y≠0} 奇函数 偶函数 奇函数 非奇非偶函数 奇函数 增函数 在(-∞,0]上单调递减,在[0,+∞)上单调递增 增函数 在[0,+∞)上单调递增 在(-∞,0)上单调递减,在(0,+∞)上单调递减
知识梳理
一般幂函数的性质
(1)函数y=xα,当α>0时,具有的性质:
①函数的图象都过点(0,0)和(1,1);
②在第一象限内,函数的图象随x的增大而上升,函数在区间[0,+∞)上是增函数.
(2)函数y=xα,当α<0时,具有的性质:
①函数的图象都过点(1,1);
②在第一象限内,函数的图象随x的增大而下降,函数在区间(0,+∞)上是减函数.
例2 (1)函数y=的图象是( )
(2)如图所示,图中的曲线是幂函数y=xn在第一象限的图象,已知n取±2,±四个值,则相应于C1,C2,C3,C4的n依次为( )
A.-2,-,,2 B.2,,-,-2
C.-,-2,2, D.2,,-2,-
答案 (1)B (2)B
解析 (1)∵当x>1时,x>;当x=1时,x=,所以A,C,D均不对,选B.
(2)根据幂函数y=xn的性质,在第一象限内的图象当n>0时,n越大,y=xn递增速度越快,故C1的n=2,C2的n=;当n<0时,|n|越大,曲线越陡峭,所以曲线C3的n=-,曲线C4的n=-2,故选B.
反思感悟 (1)幂函数图象的画法
①确定幂函数在第一象限内的图象:先根据α的取值,确定幂函数y=xα在第一象限内的图象.
②确定幂函数在其他象限内的图象:根据幂函数的定义域及奇偶性确定幂函数f(x)在其他象限内的图象.
(2)解决与幂函数有关的综合性问题的方法
首先要考虑幂函数的概念,对于幂函数y=xα(α是常数),由于α的取值不同,所以相应幂函数的单调性和奇偶性也不同.同时,注意分类讨论思想的应用.
跟踪训练2 如图是幂函数y=xm与y=xn在第一象限内的图象,则( )
A.-1
D.n<-1,m>1
答案 B
解析 由于y=xm在(0,+∞)上是增函数,且为上凸函数,故0
例3 比较下列各组数中两个数的大小:
(1)0.5与0.5;
(2)-1与-1;
(3)与.
解 (1)∵幂函数y=x0.5在(0,+∞)上是增函数,又>,
∴0.5>0.5.
(2)∵幂函数y=x-1在(-∞,0)上是减函数,
又-<-,
∴-1>-1.
(3)∵函数y1=在(0,+∞)上是增函数,
又>1,∴=1.
又∵函数y2=在(0,+∞)上是增函数,且<1,∴=1,
∴.
反思感悟 比较幂值大小的方法
(1)若两个幂值的指数相同或可化为两个指数相同的幂值时,则可构造函数,利用幂函数的单调性比较大小.
(2)若底数、指数均不同,则考虑用中间值法比较大小,这里的中间值可以是“0”或“1”.
跟踪训练3 比较下列各组数中两个数的大小:
(1)-0.3与-0.3;
(2)-3.143与-π3.
解 (1)∵y=x-0.3在(0,+∞)上是减函数,
又>,
∴-0.3<-0.3.
(2)∵y=x3是R上的增函数,且3.14<π,
∴3.143<π3,∴-3.143>-π3.
1.知识清单:
(1)幂函数的定义.
(2)几个常见幂函数的图象.
(3)幂函数的性质.
2.方法归纳:待定系数法、数形结合法.
3.常见误区:易忽略幂函数的概念.
1.已知幂函数y=f(x)的图象经过点,则f(2)等于( )
A. B.2 C. D.
答案 A
解析 设幂函数为y=xα,
∵幂函数的图象经过点,
∴=4α,∴α=-1,∴y=x-1,
∴f(2)=2-1=.
2.设α∈,则使函数y=xα的定义域是R,且为奇函数的所有α的值是( )
A.1,3 B.-1,1
C.-1,3 D.-1,1,3
答案 A
解析 当α=-1时,函数y=x-1的定义域是{x|x≠0},且为奇函数;当α=1时,函数y=x的定义域是R,且为奇函数;当α=时,函数y=的定义域是{x|x≥0},且为非奇非偶函数;当α=3时,函数y=x3的定义域是R,且为奇函数.
3.函数y=的图象是( )
答案 C
解析 ∵函数y=的定义域为[0,+∞),
∴它是非奇非偶函数,故排除A,B选项.
又>1,
∴图象在区间[0,1]上是下凸的,故排除D选项.
4.0.23-2.3与0.24-2.3的大小关系是___________________________.
答案 0.23-2.3>0.24-2.3
解析 因为函数y=x-2.3在(0,+∞)上是减函数,且0.23<0.24,
所以0.23-2.3>0.24-2.3.
1.幂函数的图象过点(16,4),则该幂函数的解析式是( )
A.y=x-1 B.y=
C.y=x2 D.y=x3
答案 B
解析 设f(x)=xα,则16α=4,
∴α=,∴f(x)=.
2.下列函数中,既是偶函数,又在区间(0,+∞)上是增函数的是( )
A.y= B.y=x-1
C.y=x2 D.y=x
答案 C
解析 由于y=x-1和y=x都是奇函数,故B,D不满足题意.y=在(0,+∞)上是增函数,但不是偶函数,故A不满足题意.y=x2为偶函数,且在(0,+∞)上是增函数,故C满足题意.
3.已知函数f(x)=,若0
解析 因为函数f(x)=在(0,+∞)上是增函数,
又0
答案 B
解析 y=的图象位于第一象限,且为增函数,所以函数图象是上升的,函数y=-1的图象可看作是由y=的图象向下平移一个单位长度得到的(如选项A中的图所示),则y=-1的图象关于x轴对称的图象即为选项B.
5.(多选)已知幂函数f(x)的图象经过点,则幂函数f(x)具有的性质是( )
A.在其定义域上为增函数
B.在(0,+∞)上是减函数
C.奇函数
D.定义域为R
答案 BC
解析 设幂函数f(x)=xα(α为常数),因为幂函数图象过点,所以f(x)=,所以由f(x)的性质知,定义域为{x∈R|x≠0},f(x)是奇函数,在(-∞,0),(0,+∞)上均是减函数.
6.(多选)下列命题不正确的是( )
A.幂函数的图象都经过(0,0),(1,1)两点
B.当n=0时,函数y=xn的图象是一条直线
C.如果两个幂函数的图象有三个交点,那么这两个函数一定相同
D.如果幂函数为偶函数,则图象一定经过点(-1,1)
答案 ABC
解析 对于A,幂函数的图象都经过点(1,1),当y=xn中n≤0时,不过点(0,0),故A不正确;对于B,当n=0时,幂函数y=xn的图象是直线y=1除去点(0,1),故B不正确;对于C,当两个幂函数的图象有三个交点时,两函数不一定相同,如y=x与y=x3的图象有三个交点,但这两个函数不相同,故C不正确;对于D,因为幂函数的图象都经过点(1,1),所以若幂函数为偶函数,其图象一定经过点(-1,1),故D正确.
7.已知2.4α>2.5α,则α的取值范围是________.
答案 α<0
解析 因为0<2.4<2.5,而2.4α>2.5α,
所以y=xα在(0,+∞)上是减函数.故α<0.
8.若幂函数y=(m2-2m-2)x-4m-2在x∈(0,+∞)上为减函数,则实数m的值是________.
答案 3
解析 因为函数y=(m2-2m-2)x-4m-2既是幂函数又是(0,+∞)上的减函数,
所以
解得m=3.
9.已知函数f(x)=(m2+2m)·,m为何值时,函数f(x)是(1)正比例函数;(2)反比例函数;(3)幂函数.
解 (1)若函数f(x)为正比例函数,
则∴m=1.
(2)若函数f(x)为反比例函数,
则∴m=-1.
(3)若函数f(x)为幂函数,则m2+2m=1,
∴m=-1±.
10.比较下列各组数的大小:
(1)和;
(2)和.
解 (1)函数y=在(0,+∞)上是减函数,
又3<3.2,所以
(2)函数y=在(0,+∞)上是增函数,
而>,所以
11.函数f(x)=+b-3是幂函数,则下列结论正确的是( )
A.f(a)>f(b) B.f(a)
答案 A
解析 ∵f(x)为幂函数,
∴解得
∴f(x)=,
∴f(x)在(0,+∞)上是增函数,且a>b>0,
∴f(a)>f(b).
12.已知幂函数y=(m∈Z)的图象与x轴和y轴没有交点,且关于y轴对称,则m等于( )
A.1 B.0,2
C.-1,1,3 D.0,1,2
答案 C
解析 ∵幂函数y=(m∈Z)的图象与x轴和y轴没有交点,且关于y轴对称,
∴m2-2m-3≤0,且m2-2m-3(m∈Z)为偶数,
由m2-2m-3≤0,得-1≤m≤3,
又m∈Z,∴m=-1,0,1,2,3.
当m=-1时,m2-2m-3=1+2-3=0,为偶数,符合题意;
当m=0时,m2-2m-3=-3,为奇数,不符合题意;
当m=1时,m2-2m-3=1-2-3=-4,为偶数,符合题意;
当m=2时,m2-2m-3=4-4-3=-3,为奇数,不符合题意;
当m=3时,m2-2m-3=9-6-3=0,为偶数,符合题意.
综上所述,m=-1,1,3.
13.若,则实数m的取值范围为________.
答案
解析 因为y=在定义域[0,+∞)上是增函数,所以
解得-1≤m<.
故m的取值范围为.
14.给出下面四个条件:①f(m+n)=f(m)+f(n);②f(m+n)=f(m)·f(n);③f(mn)=f(m)·f(n);④f(mn)=f(m)+f(n).如果m,n是幂函数y=f(x)定义域内的任意两个值,那么幂函数y=f(x)一定满足的条件的序号为________.
答案 ③
解析 设f(x)=xα,则f(m+n)=(m+n)α,
f(m)+f(n)=mα+nα,
f(m)·f(n)=mα·nα=(mn)α,
f(mn)=(mn)α,
所以f(mn)=f(m)·f(n)一定成立,其他三个不一定成立.
15.(多选)给出下列幂函数,其中满足条件f <(x1>x2>0)的函数的是( )
A.f(x)=x B.f(x)=x2
C.f(x)=x3 D.f(x)=
答案 BC
解析 A.函数f(x)=x的图象是一条直线,
故当x1>x2>0时,
f =;
B.函数f(x)=x2的图象是下凸形曲线,
故当x1>x2>0时,
f <;
C.在第一象限,函数f(x)=x3的图象是下凸形曲线,故当x1>x2>0时,
f <;
D.函数f(x)=的图象是上凸形曲线,
故当x1>x2>0时,
f >.
16.已知幂函数f(x)=在(0,+∞)上是增函数,函数g(x)=2x-k.
(1)求m的值;
(2)当x∈[1,2]时,记f(x),g(x)的值域分别为集合A,B,若A∪B=A,求实数k的取值范围.
解 (1)依题意,得(m-1)2=1,
解得m=0或m=2.
当m=2时,f(x)=x-2在(0,+∞)上是减函数,与题设矛盾,舍去,∴m=0.
(2)由(1)可知f(x)=x2.
当x∈[1,2]时,f(x),g(x)是增函数,
∴A=[1,4],B=[2-k,4-k].
∵A∪B=A,∴B A,
∴ 0≤k≤1.
∴实数k的取值范围是[0,1].
同课章节目录
- 第1章 集合
- 1.1 集合的概念与表示
- 1.2 子集、全集、补集
- 1.3 交集、并集
- 第2章 常用逻辑用语
- 2.1 命题、定理、定义
- 2.2 充分条件、必要条件、冲要条件
- 2.3 全称量词命题与存在量词命题
- 第3章 不等式
- 3.1 不等式的基本性质
- 3.2 基本不等式
- 3.3 从函数观点看一元二次方程和一元二次不等式
- 第4章 指数与对数
- 4.1 指数
- 4.2 对数
- 第5章 函数概念与性质
- 5.1 函数的概念和图象
- 5.2 函数的表示方法
- 5.3 函数的单调性
- 5.4 函数的奇偶性
- 第6章 幂函数、指数函数和对数函数
- 6.1 幂函数
- 6.2 指数函数
- 6.3 对数函数
- 第7章 三角函数
- 7.1 角与弧度
- 7.2 三角函数概念
- 7.3 三角函数的图象和性质
- 7.4 三角函数应用
- 第8章 函数应用
- 8.1 二分法与求方程近似解
- 8.2 函数与数学模型
