四年级数学下册课件 9 数学广角——鸡兔同笼 人教版(共18张PPT)
文档属性
| 名称 | 四年级数学下册课件 9 数学广角——鸡兔同笼 人教版(共18张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 585.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-07-11 10:38:14 | ||
图片预览





文档简介
(共18张PPT)
鸡兔同笼
《孙子算经》是我国古代一部较为普及的算书,许多问题浅显有趣,其中下卷第31题”雉兔同笼”流传尤为广泛,飘洋过海流传到了日本等国.
今有雉兔同笼,
上有三十五头,
下有九十四足,
问雉兔各几何
“上有三十五头”的意思是什么
“下有九十四足”的意思是什么
古题今解
例题:笼子里有若干只鸡和兔,从上面数有8个头,从下面数,有26条腿。
问:鸡和兔各有多少只?
预设:
(1)鸡在减少,兔在增加,脚也在增加。
(2)每减少1只鸡,增加1只兔,脚的总只数增加2只。
(3)每减少1只兔,增加1只鸡,脚的总只数减少2只。
(4)鸡和兔的总只数没有变。
方法一
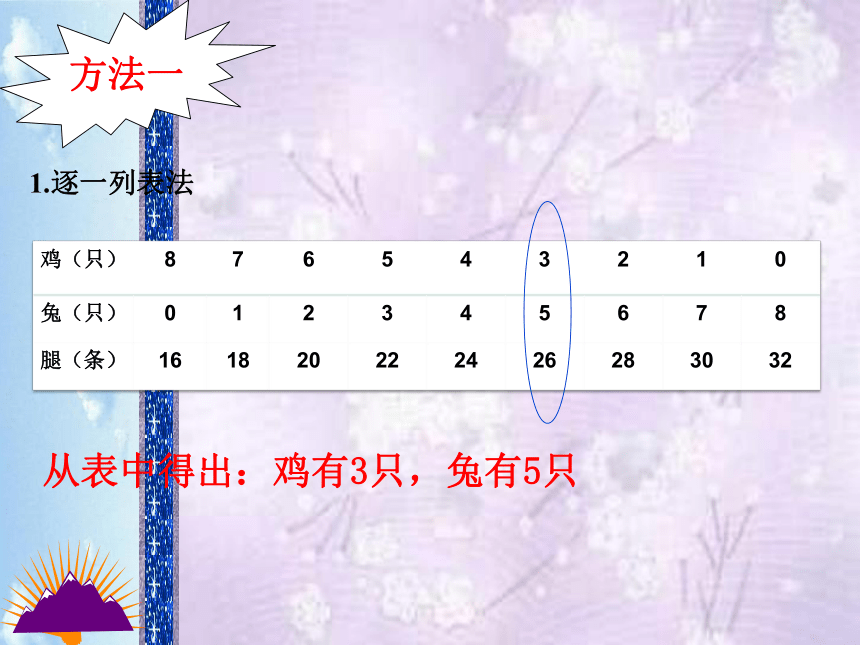
1.逐一列表法
鸡(只) 8 7 6 5 4 3 2 1 0
兔(只) 0 1 2 3 4 5 6 7 8
腿(条) 16 18 20 22 24 26 28 30 32
从表中得出:鸡有3只,兔有5只
方法二
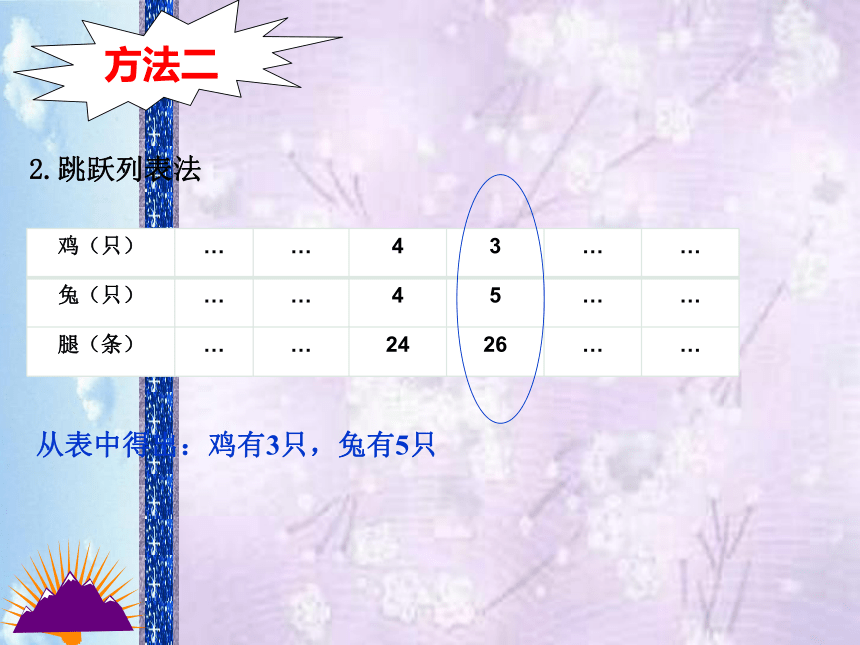
2.跳跃列表法
鸡(只) … … 4 3 … …
兔(只) … … 4 5 … …
腿(条) … … 24 26 … …
从表中得出:鸡有3只,兔有5只
方法三
3.假设法
(1)假设全是鸡:
8×2=16(条)(如果把兔全当成鸡一共就有8×2=16条腿)
26-16=10(条)(把兔看成鸡来算,4条腿兔有当成两条腿的鸡算,每只兔就少了两条腿,10条腿是少算了兔的腿)
(1)假设全是鸡:
4-2=2(假设全是鸡,是把4条腿的兔有当成两条腿的鸡。所以4-2表示是一只兔当成一只鸡就要少算2条腿)
10÷2=5(只)兔(那把多少只兔当成鸡算就会少10条腿呢?就看10里面有几个2就是把几只兔当成了鸡来算,所以10÷2=5就是兔的只数)
8-5=3(只)鸡(用鸡兔的总只数减去兔的只数就是鸡的只数,8-5=3只鸡)
【方法二】假设这8只全是兔。
8×4=32(条)(如果把鸡全看成兔一共就有8×4=32条腿)
32-26=6(条)(把鸡当成兔来算,两条腿的鸡当成4条腿兔算,每只鸡就多了两条腿,6条腿是多算了鸡的腿)
(2)假设全是兔。
4-2=2(假设全是兔,是把两条腿的鸡当成有4条腿的兔。所以4-2表示是一只鸡当成一只兔多算了2条腿)
6÷2=3(只)鸡(那要把多少只鸡当成兔来算就会多算6条腿呢?就看6里面有几个2就是把几只鸡当成了兔算,所以6÷2=3就是现在鸡的只数)
8-3=5(只)兔
(1)小明的储蓄罐里有1角和5角的硬币共7枚,价值1.5元。问:一角的硬币有几枚,5角的硬币有几枚?
答:一角硬币有( )枚,5角硬币有( )枚。
巩固练习
1.列表解决。
5角 1 2 3 0
1角 10 5 0 15
总钱数 1.5 1.5 1.5 1.5
5
2
课堂练习
(2)40名同学去划船,一共乘坐8只船,其中每只大船坐6人,每只小船坐4人。求大船和小船各几只?
答:大船( )只,小船( )只。
大船 1 2 3 4 5 6 7
小船 7 6 5 4 3 2 7
总人数 34 36 38 40 42 40 34
4
4
1.鸡兔同笼,共有14个头,38条腿,问:有几只鸡几只有兔
巩固应用
假设法:假设笼子里全都是兔。
14 ×4=56(条)
56-38=18(条)
18 ÷2=9(只)
14-9=5(只)
答:鸡有9只,兔有5只。
发展思维
3.一队强盗一队狗,二队拼作一队走,数头一共三百六,数腿一共八百九,问有多少强盗多少狗?
【讲解】假如这二队都是狗,则 360只狗,应该有腿 360×4=1440(只)腿而实际只有890只腿,总共多出来1440-890=550(只)腿狗四只腿,强盗两只腿,所以这多出来的550只腿也就是强盗的腿的数量除以2,即为强盗人的数量:550 ÷ 2 =275(个);360 - 275=85(只)即是狗的数量。
答:强盗有275个,狗有85只。
经过本节课的学习,
你有那些收获?
小结与收获
结束
鸡兔同笼问题:
假设都是兔:
(兔脚数× 总头数-实有脚数) ÷(兔脚数-鸡脚数)=鸡的只数
假设都是鸡:
(实有脚数-鸡脚数× 总头数) ÷(兔脚数-鸡脚数)=兔的只数
再见
鸡兔同笼
《孙子算经》是我国古代一部较为普及的算书,许多问题浅显有趣,其中下卷第31题”雉兔同笼”流传尤为广泛,飘洋过海流传到了日本等国.
今有雉兔同笼,
上有三十五头,
下有九十四足,
问雉兔各几何
“上有三十五头”的意思是什么
“下有九十四足”的意思是什么
古题今解
例题:笼子里有若干只鸡和兔,从上面数有8个头,从下面数,有26条腿。
问:鸡和兔各有多少只?
预设:
(1)鸡在减少,兔在增加,脚也在增加。
(2)每减少1只鸡,增加1只兔,脚的总只数增加2只。
(3)每减少1只兔,增加1只鸡,脚的总只数减少2只。
(4)鸡和兔的总只数没有变。
方法一
1.逐一列表法
鸡(只) 8 7 6 5 4 3 2 1 0
兔(只) 0 1 2 3 4 5 6 7 8
腿(条) 16 18 20 22 24 26 28 30 32
从表中得出:鸡有3只,兔有5只
方法二
2.跳跃列表法
鸡(只) … … 4 3 … …
兔(只) … … 4 5 … …
腿(条) … … 24 26 … …
从表中得出:鸡有3只,兔有5只
方法三
3.假设法
(1)假设全是鸡:
8×2=16(条)(如果把兔全当成鸡一共就有8×2=16条腿)
26-16=10(条)(把兔看成鸡来算,4条腿兔有当成两条腿的鸡算,每只兔就少了两条腿,10条腿是少算了兔的腿)
(1)假设全是鸡:
4-2=2(假设全是鸡,是把4条腿的兔有当成两条腿的鸡。所以4-2表示是一只兔当成一只鸡就要少算2条腿)
10÷2=5(只)兔(那把多少只兔当成鸡算就会少10条腿呢?就看10里面有几个2就是把几只兔当成了鸡来算,所以10÷2=5就是兔的只数)
8-5=3(只)鸡(用鸡兔的总只数减去兔的只数就是鸡的只数,8-5=3只鸡)
【方法二】假设这8只全是兔。
8×4=32(条)(如果把鸡全看成兔一共就有8×4=32条腿)
32-26=6(条)(把鸡当成兔来算,两条腿的鸡当成4条腿兔算,每只鸡就多了两条腿,6条腿是多算了鸡的腿)
(2)假设全是兔。
4-2=2(假设全是兔,是把两条腿的鸡当成有4条腿的兔。所以4-2表示是一只鸡当成一只兔多算了2条腿)
6÷2=3(只)鸡(那要把多少只鸡当成兔来算就会多算6条腿呢?就看6里面有几个2就是把几只鸡当成了兔算,所以6÷2=3就是现在鸡的只数)
8-3=5(只)兔
(1)小明的储蓄罐里有1角和5角的硬币共7枚,价值1.5元。问:一角的硬币有几枚,5角的硬币有几枚?
答:一角硬币有( )枚,5角硬币有( )枚。
巩固练习
1.列表解决。
5角 1 2 3 0
1角 10 5 0 15
总钱数 1.5 1.5 1.5 1.5
5
2
课堂练习
(2)40名同学去划船,一共乘坐8只船,其中每只大船坐6人,每只小船坐4人。求大船和小船各几只?
答:大船( )只,小船( )只。
大船 1 2 3 4 5 6 7
小船 7 6 5 4 3 2 7
总人数 34 36 38 40 42 40 34
4
4
1.鸡兔同笼,共有14个头,38条腿,问:有几只鸡几只有兔
巩固应用
假设法:假设笼子里全都是兔。
14 ×4=56(条)
56-38=18(条)
18 ÷2=9(只)
14-9=5(只)
答:鸡有9只,兔有5只。
发展思维
3.一队强盗一队狗,二队拼作一队走,数头一共三百六,数腿一共八百九,问有多少强盗多少狗?
【讲解】假如这二队都是狗,则 360只狗,应该有腿 360×4=1440(只)腿而实际只有890只腿,总共多出来1440-890=550(只)腿狗四只腿,强盗两只腿,所以这多出来的550只腿也就是强盗的腿的数量除以2,即为强盗人的数量:550 ÷ 2 =275(个);360 - 275=85(只)即是狗的数量。
答:强盗有275个,狗有85只。
经过本节课的学习,
你有那些收获?
小结与收获
结束
鸡兔同笼问题:
假设都是兔:
(兔脚数× 总头数-实有脚数) ÷(兔脚数-鸡脚数)=鸡的只数
假设都是鸡:
(实有脚数-鸡脚数× 总头数) ÷(兔脚数-鸡脚数)=兔的只数
再见
